An Experimental Investigation of Viscoelastic Flow in a Contraction Channel
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Experimental Set-Up
2.3. Computational Method and Model Description
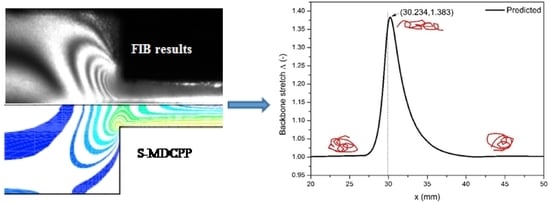
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Hooshyar, S.; Germann, N. Shear banding in 4: 1 planar contraction. Polymers 2019, 11, 417. [Google Scholar] [CrossRef] [Green Version]
- Hooshyar, S.; Germann, N. The investigation of shear banding polymer solutions in die extrusion geometry. J. Non-Newton. Fluid Mech. 2019, 272, 104161. [Google Scholar] [CrossRef]
- Ganvir, V.; Gautham, B.P.; Pol, H.; Bhamla, M.S.; Sclesi, L.; Thaokar, R.; Lele, A.; Mackley, M. Extrudate swell of linear and branched polyethylenes: ALE simulations and comparison with experiments. J. Non-Newton. Fluid Mech. 2011, 166, 12–24. [Google Scholar] [CrossRef]
- Pol, H.V.; Joshi, Y.M.; Tapadia, P.S.; Lele, A.K.; Mashelkar, R.A. A Geometrical Solution to the Sharkskin Instability. Ind. Eng. Chem. Res. 2007, 46, 3048–3056. [Google Scholar] [CrossRef]
- McLeish, T.C.B.; Larson, R.G. Molecular constitutive equations for a class of branched polymers: The pom-pom polymer. J. Rheol. 1998, 42, 81–110. [Google Scholar] [CrossRef]
- McLeish, T.C.B. Tube theory of entangled polymer dynamics. Adv. Phys. 2002, 51, 1379–1527. [Google Scholar] [CrossRef]
- Verbeeten, W.M.H.; Peters, G.W.M.; Baaijens, F.P.T. Differential constitutive equations for polymer melts: The extended Pom-Pom model. J. Rheol. 2001, 45, 823–844. [Google Scholar] [CrossRef] [Green Version]
- Clemeur, N.; Rutgers, R.P.G.; Debbaut, B. On the evaluation of some differential formulations for the Pom-Pom constitutive model. Rheol. Acta. 2003, 42, 217–231. [Google Scholar] [CrossRef]
- Tanner, R.I.; Nasseri, S. Simple constitutive models for linear and branched polymers. J. Non-Newton. Fluid Mech. 2003, 116, 1–17. [Google Scholar] [CrossRef]
- Wang, W.; Li, X.K.; Han, X.H. A numerical study of constitutive models endowed with Pom-Pom molecular attributes. J. Non-Newton. Fluid Mech. 2010, 165, 1480–1493. [Google Scholar] [CrossRef]
- Clemeur, N.; Debbaut, B. A pragmatic approach for deriving constitutive equations endowed with pom–pom attributes. Rheol. Acta. 2007, 46, 1187–1196. [Google Scholar] [CrossRef]
- Marín-Santibáñez, B.M.; Pérez-González, J.; Gómez-Herrera, G.; Rodríguez-González, F. Capillary extrusion of polypropylene/high-density polyethylene immiscible blends as studied by rheo-particle image velocimetry. Polym. Test. 2020, 84, 106390. [Google Scholar] [CrossRef]
- Clemeur, N.; Rutgers, R.P.G.; Debbaut, B. Numerical simulation of abrupt contraction flows using the Double Convected Pom–Pom model. J. Non-Newton. Fluid Mech. 2004, 117, 193–209. [Google Scholar] [CrossRef]
- Verbeeten, W.M.H.; Peters, G.W.M.; Baaijens, F.P.T. Viscoelastic Analysis of Complex Polymer Melt Flows using the eXtended Pom-Pom model. J. Non-Newton. Fluid Mech. 2002, 108, 301–326. [Google Scholar] [CrossRef]
- Verbeeten, W.M.H.; Peters, G.W.M.; Baaijens, F.P.T. Numerical simulations of the planar contraction flow for a polyethylene melt using the XPP model. J. Non-Newton. Fluid Mech. 2004, 117, 73–84. [Google Scholar] [CrossRef]
- Wang, X.L.; Chen, R.H.; Wang, M.M.; Jin, G. Validation of Double Convected Pom-Pom Model With Particle Image Velocimetry Technique. Polym. Eng. Sci. 2015, 55, 1897–1905. [Google Scholar] [CrossRef]
- Owens, R.G.; Phillips, T.N. Computational Rheology; Imperial College Press: London, UK, 2002; pp. 201–246. [Google Scholar]
- Aguayo, J.P.; Tamaddon-Jahromi, H.R.; Webster, M.F. Extensional response of the pom-pom model through planar contraction flows for branched polymer melts. J. Non-Newton. Fluid Mech. 2006, 134, 105–126. [Google Scholar] [CrossRef]
- Aguayo, J.P.; Phillips, P.M.; Phillips, T.N.; Tamaddon-Jahromi, H.R.; Snigerev, B.A.; Webster, M.F. The numerical prediction of planar viscoelastic contraction flows using the pom-pom model and higher-order finite volume schemes. J. Comput. Phys. 2007, 220, 586–611. [Google Scholar] [CrossRef]
- Wang, W.; Wang, X.P.; Hu, C.X. A comparative study of viscoelastic planar contraction flow for polymer melts using molecular constitutive models. Korea-Aust. Rheol. J. 2014, 26, 365–375. [Google Scholar] [CrossRef]
- Wang, W.; Hu, C.X.; Li, W.W. Time-dependent rheological behavior of branched polymer melts in extensional flows. Mech. Time-Depend. Mater. 2016, 20, 123–137. [Google Scholar] [CrossRef]
- Li, X.K.; Han, X.H. Numerical modeling of viscoelastic flows using equal low-order finite elements. Comput. Meth. Appl. Mech. Engrg. 2010, 199, 570–581. [Google Scholar] [CrossRef]
- Oñate, E. A stabilized finite element method for incompressible viscous flows using a finite increment calculus formulation. Comput. Meth. Appl. Mech. Engrg. 2000, 182, 355–370. [Google Scholar] [CrossRef] [Green Version]
- Li, X.K.; Han, X.H. An iterative stabilized fractional step algorithm for numerical solution of incompressible N–S equations. Int. J. Numer. Meth. Fluids. 2005, 49, 395–416. [Google Scholar] [CrossRef]
- Guénette, R.; Fortin, M. A new mixed finite element method for computing viscoelastic flows. J. Non-Newton. Fluid Mech. 1995, 60, 27–52. [Google Scholar] [CrossRef]
- Brooks, A.N.; Hughes, T.J.R. Streamline upwind/Petrov–Galerkin methods for convection dominated flows with particular emphasis on the incompressible Navier–Stokes equations. Comput. Meth. Appl. Mech. Engrg. 1982, 32, 199–259. [Google Scholar] [CrossRef]
- Verbeeten, W.M.H. Computational Polymer Melt Rheology. Ph.D. Thesis, Technische Universiteit Eindhoven, Eindhoven, The Netherlands, 2001. [Google Scholar]














| Density (kg/m3) | Mw | Mw/Mn | Melt Index (dg/min) | |
|---|---|---|---|---|
| LDPE (Stamylan LD 2008 XC43) | 920 | 155,000 | 11.92 | 8 |
| S–MDCPP Model | |||||
|---|---|---|---|---|---|
| Mode | Maxwell Parameters | Nonlinear Parameters | |||
| G (Pa) | λ0b (s) | q = 2/ν | r | ξ | |
| 1 | 1.0377 × 104 | 0.40 | 10 | 1.2 | 0.02 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, W.; Wang, L. An Experimental Investigation of Viscoelastic Flow in a Contraction Channel. Polymers 2021, 13, 1876. https://doi.org/10.3390/polym13111876
Wang W, Wang L. An Experimental Investigation of Viscoelastic Flow in a Contraction Channel. Polymers. 2021; 13(11):1876. https://doi.org/10.3390/polym13111876
Chicago/Turabian StyleWang, Wei, and Linlin Wang. 2021. "An Experimental Investigation of Viscoelastic Flow in a Contraction Channel" Polymers 13, no. 11: 1876. https://doi.org/10.3390/polym13111876
APA StyleWang, W., & Wang, L. (2021). An Experimental Investigation of Viscoelastic Flow in a Contraction Channel. Polymers, 13(11), 1876. https://doi.org/10.3390/polym13111876