Phase Equilibrium and Interdiffusion in Blends of Polystyrene with Polyacrylates
Abstract
:1. Introduction
2. Experimental
2.1. Sample Preparation
2.2. Characterization Method
3. Results and Discussion
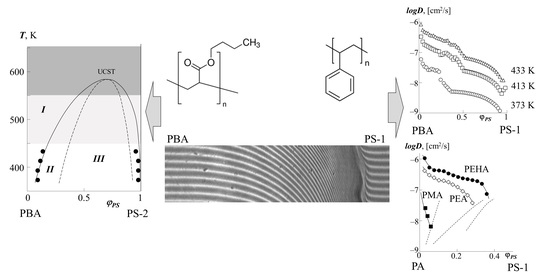
3.1. Conjugate Phase Zones
3.2. Phase State Diagram
- At the first stage of the analysis of the diagrams by Equation (1) and the coexisting phase compositions, the values of the Flory–Huggins parameter χ were estimated under the assumption of the absence of its concentration dependence.The obtained values of χ are the averaged value for the paired parameters of the interaction and . Here, and are the volume concentrations of PS and PA, respectively, the indices ′ and ″ refer to different coexisting phases, and are their degrees of polymerization.
- At the second stage, the critical value of the Flory–Huggins parameter χcr was calculated:
- Then, the temperature dependences of the pair parameter were plotted in the coordinates χ–1/T (Figure 6), which were extrapolated to the values of χcr. The point of intersection of these lines was taken for UCST.
- The critical concentration φcr was determined from the point of intersection of the Alekseev’s diameter and the isotherm corresponding to the UCST.
- The dome of the binodal curve and the spinodal curves separating the regions of metastable and labile solutions were calculated using the binodal and spinodal equations in the framework of the Flory–Huggins theory (shown in Figure 7).
- In addition, the temperature-concentration field of the diagrams contains limiting regions characterizing the region of thermal stability of homopolymers and their blends.
3.3. Diffusion
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Min, T.I.; Klein, A.; El-Aasser, M.S.; Vanderhoff, J.W. Morphology and grafting in polybutylacrylate-polystyrene core-shell emulsion polymerization. J. Polym. Sci. Polym. Chem. Ed. 1983, 21, 2845–2861. [Google Scholar] [CrossRef]
- Mellinger, F.; Wilhelm, M.; Landfester, K.; Spiess, H.W.; Haunschild, A.; Packusch, J. Structure of water-containing latexes: Remagnetization effects during solid-state nmr spin-diffusion experiments. Acta Polym. 1998, 49, 108–115. [Google Scholar] [CrossRef]
- Braun, D.; Rüger, W.; Hellmann, G.P. Morphology and strength of elastic films of structured latices. J. Macromol. Sci. Part B 1999, 38, 1071–1079. [Google Scholar] [CrossRef]
- Wagner, J.; Härtl, W.; Walderhaug, H. Long time self-diffusion in suspensions of highly charged colloids: A comparison between pulsed field gradient NMR and Brownian dynamics. J. Chem. Phys. 2001, 114, 975. [Google Scholar] [CrossRef]
- Huo, D.; Liu, D. Morphologies of polybutylacrylate/poly(styrene-co-methyl methacrylate) latex prepared by starved emulsion polymerization Part I. Thermodynamics equilibrium morphology. Polym. Int. 2002, 51, 585–593. [Google Scholar] [CrossRef]
- Wagner, J.; Härtl, W.; Lellig, C.; Hempelmann, R.; Walderhaug, H. Complex liquids consisting of low-TG polymer-colloids: Structure and self-diffusion. J. Mol. Liq. 2002, 98–99, 183–190. [Google Scholar] [CrossRef]
- Tang, E.; Tian, B.; Fu, C. Apparent kinetic study of latex interpenetrating polymer networks P(ethyl acrylate)/P(styrene) and P(styrene)/P (ethyl acrylate) by two stage emulsion polymerization. Colloids Surfaces A: Physicochem. Eng. Asp. 2009, 333, 7–11. [Google Scholar] [CrossRef]
- Ianchiş, R.; Donescu, D.; Corobea, M.C.; Petcu, C.; Ghiurea, M.; Serban, S.; Radovici, C. Synthesis of polystyrene/polybutylacrylate/layered silicate nanocomposites in aqueous medium. Colloid Polym. Sci. 2010, 288, 1215–1224. [Google Scholar] [CrossRef]
- Park, D.-K.; Park, S.-J.; Baek, W.-I.; Kanjwal, M.A.; Kim, H.-Y. Point-bonded electrospun polystyrene fibrous mats fabricated via the addition of poly(butylacrylate) adhesive. Polym. Eng. Sci. 2011, 51, 894–901. [Google Scholar] [CrossRef]
- Runyon, J.R.; Williams, S.K.R. Composition and molecular weight analysis of styrene-acrylic copolymers using thermal field-flow fractionation. J. Chromatogr. A 2011, 1218, 6774–6779. [Google Scholar] [CrossRef] [PubMed]
- Lee, K.-H.; Ryu, S.-W. Room temperature baroplastic processing of PS/PBA nano-blends. Macromol. Res. 2012, 20, 1294–1299. [Google Scholar] [CrossRef]
- Ibrahim, S.; Refaat, Y.; Nassar, M. Synthesis and characterization of nanostructured polysty-rene/polybutylacrylate copolymer coating. Egypt. J. Chem. 2015, 58, 509–520. [Google Scholar]
- Paul, D.R.; Newman, S. Polymer Blends; Academic Press: Cambridge, MA, USA, 1978. [Google Scholar]
- Paul, D.R.; Bucknall, C.B. Polymer Blends; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2000. [Google Scholar]
- Somani, R.H.; Shaw, M.T. Miscibility of acrylic polymers in polystyrene by melt titration. Macromolecules 1981, 14, 1549–1554. [Google Scholar] [CrossRef]
- Malkin, A.Y.; Kuleznev, V.N. (Eds.) Multicomponent Polymer Systems; Chemistry Publishing House: Moscow, Russia, 1974. (In Russian) [Google Scholar]
- Kuleznev, V.N. Polymer Blends; Chemistry Publishing House: Moscow, Russia, 1980. (In Russian) [Google Scholar]
- Chalykh, A.E.; Gerasimov, V.K.; Mikhailov, Y.M. Phase State Diagrams of Polymer Systems; Yanus-K: Moscow, Russia, 1998. (In Russian) [Google Scholar]
- Chalykh, A.E.; Nikulova, U.; Shcherbina, A. Phase equilibria in a polystyrene-poly(butyl acrylate) system. Polym. Sci. Ser. A 2015, 57, 445–451. [Google Scholar] [CrossRef]
- Chalykh, A.E.; Nikulova, U.V.; Shcherbina, A.A.; Chernikova, E.V. Diffusion and Thermodynamics of Mixing of Polystyrene with Statistical Copolymers of Butyl Acrylate and Styrene. Polym. Sci. Ser. A 2019, 61, 175–185. [Google Scholar] [CrossRef]
- Chalykh, A.E.; Nikulova, U.V.; Gerasimov, V.K.; Khasbiullin, R. Phase Structure of Block and Gradient Copolymers of Butyl Acrylate and Styrene. Polym. Sci. Ser. A 2020, 62, 85–93. [Google Scholar] [CrossRef]
- Chalykh, A.E.; Nikulova, U.V.; Shcherbina, A.A. Diffusion and Thermodynamics of Polystyrene Mixing with Block and Gradient Copolymers of Butyl Acrylate and Styrene. Polym. Sci. Ser. A 2020, 62, 368–382. [Google Scholar] [CrossRef]
- Green, P.F. Translational dynamics of macromolecules in melts. In Diffusion in Polymers; Neogi, P., Ed.; CRC Press: Boca Raton, FL, USA, 1996; pp. 251–302. [Google Scholar]
- Chalykh, A.; Sapozhnikova, I.N. Phase Equilibria and Mutual Diffusion in Polymer—Polymer Systems with Chlorine-containing Components. Russ. Chem. Rev. 1984, 53, 1062–1077. [Google Scholar] [CrossRef]
- Van Krevelen, D.W.; Klaas, T.N. Properties of Polymers Their Correlation with Chemical Structure. Their Numerical Estimation and Prediction from Additive Group Contributions; Elsevier Science: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Malkin, A.; Ascadsky, A.; Kovriga, V.; Chalykh, A.E. Experimental Methods of Polymer Physics; MIR Publishers: Moscow, Russia, 1983. (In Russian) [Google Scholar]
- Chalykh, A.E.; Zagaitov, A.L.; Korotchrnko, D.P. Optical Diffusiometer; IFKh RAN: Moscow, Russia, 1996. (In Russian) [Google Scholar]
- Chalykh, A.E. Diffusion in Polymer Systems; Chemistry Publishing House: Moscow, Russia, 1987. (In Russian) [Google Scholar]
- Nikulova, U.V.; Chalykh, A.E. Thermodynamic analysis of the phase equilibrium of the polystyrene-poly(vinyl methyl ether) system. J. Appl. Polym. Sci. 2020, 138, 49717. [Google Scholar] [CrossRef]
- Tager, A.A. Physicochemistry of Polymers; Scientific World: Moscow, Russia, 2007. (In Russian) [Google Scholar]
- Chalykh, A.E.; Gerasimov, V.K.; Nikulova, U.V. Temperature dependence of the flory-huggins parameter and the relationship between its enthalpy and entropy components. Bull. Russ. Acad. Nat. Sci. 2020, 20, 19–26. [Google Scholar]
- Bekman, I.N. Diffusion Mathematics: Tutorial; OntoPrint: Moscow, Russia, 2016. (In Russian) [Google Scholar]
- Tsvetkov, V.E.; Eskin, S.; Frenkel, Y. The Structure of Macromolecules in Solutions; Nauka Publishing House: Moscow, Russia, 1964. [Google Scholar]
- Foreman, P.B. Acrylic Adhesives. In Handbook of Pressure-Sensitive Adhesives and Products. Technology of Pressure-Sensitive Adhesives and Products; Benedek, I., Feldstein, M.M., Eds.; CRC Press: Boca Raton, FL, USA, 2009. [Google Scholar]
- Plate, N.A. Shibaev, V.P. Comb-Like Polymers and Liquid Crystals; Publishing House: Moscow, Russia, 1980. (In Russian) [Google Scholar]
- Plate, N.A.; Litmanovich, A.D.; Kudryavtsev, Y.V. Macromolecular Reactions in Polymer Melts and Blends: Theory and Experiment; A.V. Topchiev Institute of Petrochemical Synthesis RAS: Moscow, Russia, 2008; p. 380. ISBN 9785020366718. (In Russian) [Google Scholar]













| Polymer | Brand | Mw | Mw/Mn | Tg *, K | nC | Mfg | ρ **, g/cm3 |
|---|---|---|---|---|---|---|---|
| PS-1 | PSS | 1220 | 1.07 | 343 | - | 104 | 1.04 |
| PS-2 | Aldrich | 4120 | 1.01 | 353 | - | 104 | 1.04 |
| PMA | NII Polymerov Dzerzhinsk, Russia | 32,921 | 4.47 | 282 | 1 | 86 | 1.22 |
| PEA | NII Polymerov Dzerzhinsk, Russia | 21,437 | 3.00 | 250 | 2 | 100 | 1.12 |
| PBA | NII Polymerov Dzerzhinsk, Russia | 26,195 | 3.33 | 218 | 4 | 128 | 1.04 |
| PEHA | NII Polymerov Dzerzhinsk, Russia | 19,824 | 2.86 | 188 | 8 | 140 | 0.74 |
| System | Ea, kJ/mol | System | Ea, kJ/mol |
|---|---|---|---|
| PBA–PS-1 | 15.4 | PBA–PS-2 | 34.7 |
| PEA–PS-1 | 14.1 | PEA–PS-2 | 26.4 |
| PMA–PS-1 | 12.9 | PMA–PS-2 | 20.1 |
| PEHA–PS-1 | 20.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nikulova, U.V.; Chalykh, A.E. Phase Equilibrium and Interdiffusion in Blends of Polystyrene with Polyacrylates. Polymers 2021, 13, 2283. https://doi.org/10.3390/polym13142283
Nikulova UV, Chalykh AE. Phase Equilibrium and Interdiffusion in Blends of Polystyrene with Polyacrylates. Polymers. 2021; 13(14):2283. https://doi.org/10.3390/polym13142283
Chicago/Turabian StyleNikulova, Uliana V., and Anatoly E. Chalykh. 2021. "Phase Equilibrium and Interdiffusion in Blends of Polystyrene with Polyacrylates" Polymers 13, no. 14: 2283. https://doi.org/10.3390/polym13142283
APA StyleNikulova, U. V., & Chalykh, A. E. (2021). Phase Equilibrium and Interdiffusion in Blends of Polystyrene with Polyacrylates. Polymers, 13(14), 2283. https://doi.org/10.3390/polym13142283