Influence of Ambient Temperature on Radiative and Convective Heat Dissipation Ratio in Polymer Heat Sinks
Abstract
:1. Introduction
2. Materials and Methods
2.1. Geometry of Tested Heat Sinks
2.2. Measurement Description
3. Measurement Uncertainty Analysis
4. Results
4.1. Temperature Comparison
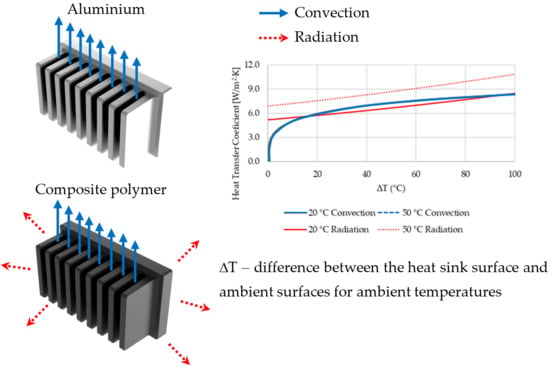
4.2. Convection-Radiation Heat Transfer Comparison
4.3. Convection-Radiation Heat Transfer Comparison
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bohacek, J.; Raudensky, M.; Kroulikova, T.; Karimi-Sibaki, E. Polymeric hollow fibers: A supercompact cooling of Li-ion cells. Int. J. Therm. Sci. 2019, 146, 1–12. [Google Scholar] [CrossRef]
- Raudensky, M.; Astrouski, I.; Brozova, T.; Bartuli, E. Flexible Polymeric Hollow Fiber Heat Exchangers for Electronic Systems. In Proceedings of the Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm 2016), Las Vegas, NV, USA, 31 May–3 June 2016; pp. 1143–1147. [Google Scholar]
- Krouliková, T.; Kudelová, T.; Bartuli, E.; Vancura, J.; Astrouski, I. Comparison of a Novel Polymeric Hollow Fiber Heat Exchanger and a Commercially Available Metal Automotive Radiator. Polymers 2021, 13, 1175. [Google Scholar] [CrossRef] [PubMed]
- Heinle, C.; Drummer, D. Potential of thermally conductive polymers for the cooling of mechatronic parts. Phys. Procedia 2010, 5, 735–744. [Google Scholar] [CrossRef] [Green Version]
- Ali, Z.; Gao, Y.; Tang, B.; Wu, X.; Wang, Y.; Li, M.; Hou, X.; Li, L.; Jiang, N.; Yu, J. Preparation, Properties and Mechanisms of Carbon Fiber/Polymer Composites for Thermal Management Applications. Polymers 2021, 13, 169. [Google Scholar] [CrossRef] [PubMed]
- Leung, S.N. Thermally conductive polymer composites and nanocomposites: Processing-structure-property relationships. Compos. Part B Eng. 2018, 150, 78–92. [Google Scholar] [CrossRef]
- Ma, J.; Shang, T.; Ren, L.; Yao, Y.; Zhang, T.; Xie, J.; Zhang, B.; Zeng, X.; Sun, R.; Xu, J.-B. Through-plane assembly of carbon fibers into 3D skeleton achieving enhanced thermal conductivity of a thermal interface material. Chem. Eng. J. 2020, 380, 122550. [Google Scholar] [CrossRef]
- Tsekmes, I.A.; Kochetov, R.; Morshuis, P.; Smit, J.J. Thermal conductivity of polymeric composites: A review. In Proceedings of the 2013 IEEE International Conference on Solid Dielectrics (ICSD), Bologna, Italy, 30 June–4 July 2013; pp. 678–681. [Google Scholar]
- Chen, H.; Ginzburg, V.; Yang, J.; Yang, Y.; Liu, W.; Huang, Y.; Du, L.; Chen, B. Thermal conductivity of polymer-based composites: Fundamentals and applications. Prog. Polym. Sci. 2016, 59, 41–85. [Google Scholar] [CrossRef]
- Yang, Q.; Zhang, Z.; Gong, X.; Yao, E.; Liu, T.; Zhang, Y.; Zou, H. Thermal conductivity of Graphene-polymer composites: Implications for thermal management. Heat Mass Transf. 2020, 56, 1931–1945. [Google Scholar] [CrossRef]
- Kim, H.S.; Bae, H.S.; Yu, J.; Kim, S.Y. Thermal conductivity of polymer composites with the geometrical characteristics of graphene nanoplatelets. Sci. Rep. 2016, 6, 26825. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Guzej, M.; Zachar, M.; Kominek, J.; Kotrbacek, P.; Brachna, R. Importance of Melt Flow Direction during Injection Molding on Polymer Heat Sinks’ Cooling Efficiency. Polymers 2021, 13, 1186. [Google Scholar] [CrossRef] [PubMed]
- Alomar, O.R.; Yousif, Q.A.; Mohamed, I.A. Numerical Simulation of Natural Convection and Radiation on Performance of uniform Fins Geometry. In Proceedings of the 2019 International Conference on Advanced Science and Engineering (ICOASE), Duhok, Iraq, 2–4 April 2019; pp. 208–213. [Google Scholar]
- Huang, L.; Shih, Y.; Shi, F.; Janicki, M.; Zubert, M.; Napieralski, A. Cooling strategy for LED filament bulb utilizing thermal radiation cooling and open slots enhancing thermal convection. In Proceedings of the 16th IEEE Intersociety Conference on Thermal and Thermomechanical Phenomena in Electronic Systems (ITherm), Orlando, FL, USA, 30 May–2 June 2017; pp. 1030–1033. [Google Scholar]
- Samson, A.; Torzewicz, T.; Raszkowski, T.; Janicki, M.; Zubert, M.; Napieralski, A. Modelling of average radiation and convection heat transfer coefficient value in electronic systems. In Proceedings of the 2016 MIXDES-23rd International Conference Mixed Design of Integrated Circuits and Systems, Lodz, Poland, 23–25 June 2016; pp. 271–275. [Google Scholar]
- Bravo, R.H.; Sanchez, A.; Chen, C.-J.; Smith, T.F. Convection and radiation heat transfer analysis in three-dimensional arrays of electronic components. In Proceedings of the 1992 Intersociety Conference on Thermal Phenomena in Electronic Systems, Austin, TX, USA, 5–8 February 1992; pp. 149–154. [Google Scholar]
- Incropera, F.P.; Dewitt, D.P.; Bergman, T.L.; Lavine, A.S. Fundamentals of Heat and Mass Transfer, 6th ed.; John Wiley & Sons: New York, NY, USA, 2007. [Google Scholar]










| Default Position (°C) | Upside-Down (°C) | Position Difference (°C) | |
|---|---|---|---|
| Melt entrance along the longer base’s edge (parallel to fins) | 99.0 (A) | 97.1 (B) | 1.9 (A)-(B) |
| Melt entrance along the shorter base’s edge (perpendicular to fins) | 100.3 (C) | 100.5 (D) | 0.2 (D)-(C) |
| Melt Entry Difference (°C) | 1.5 (C)-(A) | 3.4 (D)-(B) |
| Default Position (°C) | Upside-Down (°C) | Position Difference (°C) | |
|---|---|---|---|
| Melt entrance along the longer base’s edge (parallel to fins) | 72.3 (A) | 69.5 (B) | 2.8 (A)-(B) |
| Melt entrance along the shorter base’s edge (perpendicular to fins) | 76.1 (C) | 76.2 (D) | 0.1 (D)-(C) |
| Melt Entry Difference (°C) | 3.9 (C)-(A) | 6.7 (D)-(B) |
| Heat Sink | Melt Entering Parallelly to Fins (Default Position) (A) | Melt Entering Parallelly to Fins (Upside-Down Position) (B) | ||
|---|---|---|---|---|
| Ambient temperature (°C) | 20 | 50 | 20 | 50 |
| Convective heat flow (W) | 7.7 | 6.8 | 7.6 | 6.9 |
| Radiative heat flow (W) | 3.2 | 3.8 | 3.1 | 3.9 |
| Total heat flow (W) | 10.9 | 10.5 | 10.8 | 10.7 |
| Heat Sink | Melt Entering Perpendicularly to Fins (Default Position) (C) | Melt Entering Perpendicularly to Fins (Upside-Down Position) (D) | ||
|---|---|---|---|---|
| Ambient temperature (°C) | 20 | 50 | 20 | 50 |
| Convective heat flow (W) | 7.2 | 6.1 | 7.2 | 6.0 |
| Radiative heat flow (W) | 2.9 | 3.4 | 3.0 | 3.4 |
| Total heat flow (W) | 10.1 | 9.5 | 10.2 | 9.4 |
| Heat Sink | Heater Temperature for Ambient Temperature 20 °C (°C) | Heater Temperature for Ambient Temperature 50 °C (°C) | Difference (°C) |
|---|---|---|---|
| Aluminum | 65.7 | 95.6 | 29.9 |
| Polymer made with melt flow along fins (B) | 69.5 | 97.1 | 27.6 |
| Polymer made with melt flow perpendicular to fins (D) | 76.1 | 100.3 | 24.2 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kominek, J.; Zachar, M.; Guzej, M.; Bartuli, E.; Kotrbacek, P. Influence of Ambient Temperature on Radiative and Convective Heat Dissipation Ratio in Polymer Heat Sinks. Polymers 2021, 13, 2286. https://doi.org/10.3390/polym13142286
Kominek J, Zachar M, Guzej M, Bartuli E, Kotrbacek P. Influence of Ambient Temperature on Radiative and Convective Heat Dissipation Ratio in Polymer Heat Sinks. Polymers. 2021; 13(14):2286. https://doi.org/10.3390/polym13142286
Chicago/Turabian StyleKominek, Jan, Martin Zachar, Michal Guzej, Erik Bartuli, and Petr Kotrbacek. 2021. "Influence of Ambient Temperature on Radiative and Convective Heat Dissipation Ratio in Polymer Heat Sinks" Polymers 13, no. 14: 2286. https://doi.org/10.3390/polym13142286
APA StyleKominek, J., Zachar, M., Guzej, M., Bartuli, E., & Kotrbacek, P. (2021). Influence of Ambient Temperature on Radiative and Convective Heat Dissipation Ratio in Polymer Heat Sinks. Polymers, 13(14), 2286. https://doi.org/10.3390/polym13142286