On the Influence of Viscoelastic Modeling in Fluid Flow Simulations of Gum Acrylonitrile Butadiene Rubber
Abstract
:1. Introduction
2. Materials and Methods
2.1. Material
2.2. Rheological Testing
2.2.1. SAOS
2.2.2. High Pressure Capillary Rheometry
2.3. Constitutive and Numerical Modeling
3. Results and Discussion
3.1. Rheological Testing and Constitutive Modeling
3.2. Numerical Modeling and Evaluation
4. Summary and Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix




| Mode | ||||
|---|---|---|---|---|
| 1 | 1.0000 × 10−5 | 1.6671 × 105 | 0.1252 | 0.25 |
| 2 | 7.1969 × 10−5 | 1.6671 × 105 | ||
| 3 | 5.1795 × 10−3 | 1.6671 × 105 | ||
| 4 | 3.7276 × 10−3 | 1.6671 × 105 | ||
| 5 | 2.6827 × 10−2 | 1.6671 × 105 | ||
| 6 | 1.9307 × 10−1 | 7.4994 × 104 | ||
| 7 | 1.3895 × 10−0 | 2.9212 × 104 | ||
| 8 | 1.0000 × 101 | 2.3313 × 104 |
| Mode | ||||
|---|---|---|---|---|
| 1 | 1.0000 × 10−5 | 2.3535 × 105 | 0.1850 | 0.14 |
| 2 | 7.1969 × 10−5 | 2.3535 × 105 | ||
| 3 | 5.1795 × 10−3 | 2.3535 × 105 | ||
| 4 | 3.7276 × 10−3 | 2.3535 × 105 | ||
| 5 | 2.6827 × 10−2 | 2.3535 × 105 | ||
| 6 | 1.9307 × 10−1 | 1.0004 × 104 | ||
| 7 | 1.3895 × 100 | 3.9518 × 104 | ||
| 8 | 1.0000 × 101 | 3.0996 × 104 |
| Mode | ||||
|---|---|---|---|---|
| 1 | 1.0000 × 10−5 | 1.6671 × 105 | 0.1260 | 0.20 |
| 2 | 7.1969 × 10−5 | 1.6671 × 105 | ||
| 3 | 5.1795 × 10−3 | 1.6671 × 105 | ||
| 4 | 3.7276 × 10−3 | 1.6671 × 105 | ||
| 5 | 2.6827 × 10−2 | 1.6671 × 105 | ||
| 6 | 1.9307 × 10−1 | 7.4994 × 104 | ||
| 7 | 1.3895 × 100 | 2.9212 × 104 | ||
| 8 | 1.0000 × 101 | 2.3313 × 104 |



| 5.076 × 104 | 1.31 × 10−1 | 9.095 × 10−1 |
| 8.467 × 102 | 1.55 × 10−3 | 1.254 × 10−1 |
References
- Mitsoulis, E.; Battisti, M.; Neunhäuserer, A.; Perko, L.; Friesenbichler, W. Flow behavior of PP-polymer nanocomposites in injection molding hyperbolical dies. Adv. Polym. Technol. 2018, 37, 3045–3055. [Google Scholar] [CrossRef]
- Mitsoulis, E. 50 Years of the K-BKZ Constitutive Relation for Polymers. ISRN Polym. Sci. 2013, 2013, 952379. [Google Scholar] [CrossRef]
- Larson, R.G. Constitutive Equations for Polymer Melts and Solutions; Butterworth-Heinemann: Boston, MA, USA, 1988; ISBN 9781483162867. [Google Scholar]
- Giesekus, H. A simple constitutive equation for polymer fluids based on the concept of deformation-dependent tensorial mobility. J. Non-Newton. Fluid Mech. 1982, 11, 69–109. [Google Scholar] [CrossRef]
- Oldroyd, J.G. On the formulation of rheological equations of state. Proc. R. Soc. Lond. A 1950, 200, 523–541. [Google Scholar] [CrossRef]
- McLeish, T.C.B.; Larson, R.G. Molecular constitutive equations for a class of branched polymers: The pom-pom polymer. J. Rheol. 1998, 42, 81–110. [Google Scholar] [CrossRef]
- Phan-Thien, N. A Nonlinear Network Viscoelastic Model. J. Rheol. 1978, 22, 259–283. [Google Scholar] [CrossRef]
- Leonov, A.I. On the rheology of filled polymers. J. Rheol. 1990, 34, 1039–1068. [Google Scholar] [CrossRef]
- Kaye, A. Non-Newtonian Flow in Incompressible Fluids; Aerospace Engineering Reports; College of Aeronautics Cranfield: Cranfield, UK, 1962. [Google Scholar]
- Doi, M.; Edwards, S.F. The Theory of Polymer Dynamics; Clarendon Press: Oxford, UK, 1986; ISBN 9780198519768. [Google Scholar]
- Lodge, A.S. A network theory of flow birefringence and stress in concentrated polymer solutions. Trans. Faraday Soc. 1956, 52, 120. [Google Scholar] [CrossRef]
- Bernstein, B.; Kearsley, E.A.; Zapas, L.J. A Study of Stress Relaxation with Finite Strain. Trans. Soc. Rheol. 1963, 7, 391–410. [Google Scholar] [CrossRef]
- de Gennes, P.G. Reptation of a Polymer Chain in the Presence of Fixed Obstacles. J. Chem. Phys. 1971, 55, 572–579. [Google Scholar] [CrossRef]
- Verbeeten, W.M.H.; Peters, G.W.M.; Baaijens, F.P.T. Differential constitutive equations for polymer melts: The extended Pom–Pom model. J. Rheol. 2001, 45, 823–843. [Google Scholar] [CrossRef] [Green Version]
- Tanner, R.I.; Nasseri, S. Simple constitutive models for linear and branched polymers. J. Non-Newton. Fluid Mech. 2003, 116, 1–17. [Google Scholar] [CrossRef]
- Tanner, R.I. From A to (BK)Z in Constitutive Relations. J. Rheol. 1988, 32, 673–702. [Google Scholar] [CrossRef]
- Wagner, M.H. Analysis of time-dependent non-linear stress-growth data for shear and elongational flow of a low-density branched polyethylene melt. Rheol. Acta 1976, 15, 136–142. [Google Scholar] [CrossRef]
- Wagner, M.H. Zur Netzwerktheorie von Polymer-Schmelzen. Rheol. Acta 1979, 18, 33–50. [Google Scholar] [CrossRef]
- Mitsoulis, E. Effect of Viscoelasticity in Fountain Flow of Polyethylene Melts. Int. Polym. Process. 2009, 24, 439–451. [Google Scholar] [CrossRef] [Green Version]
- Konaganti, V.K.; Ansari, M.; Mitsoulis, E.; Hatzikiriakos, S.G. The effect of damping function on extrudate swell. J. Non-Newton. Fluid Mech. 2016, 236, 73–82. [Google Scholar] [CrossRef]
- Ansari, M.; Mitsoulis, E.; Hatzikiriakos, S.G. Capillary Extrusion and Swell of a HDPE Melt Exhibiting Slip. Adv. Polym. Technol. 2013, 32, E369–E385. [Google Scholar] [CrossRef]
- Konaganti, V.K.; Derakhshandeh, M.; Ebrahimi, M.; Mitsoulis, E.; Hatzikiriakos, S.G. Non-isothermal extrudate swell. Phys. Fluids 2016, 28, 123101. [Google Scholar] [CrossRef]
- Ansari, M.; Zisis, T.; Hatzikiriakos, S.G.; Mitsoulis, E. Capillary flow of low-density polyethylene. Polym. Eng. Sci. 2012, 52, 649–662. [Google Scholar] [CrossRef]
- Ansari, M.; Hatzikiriakos, S.G.; Mitsoulis, E. Slip effects in HDPE flows. J. Non-Newton. Fluid Mech. 2011. [Google Scholar] [CrossRef]
- Stieger, S.; Kerschbaumer, R.C.; Mitsoulis, E.; Fasching, M.; Berger-Weber, G.R.; Friesenbichler, W.; Sunder, J. Contraction and capillary flow of a carbon black filled rubber compound. Polym. Eng. Sci. 2020, 60, 32–43. [Google Scholar] [CrossRef] [Green Version]
- Stieger, S. Development of the Exjection Process for Rubbers Taking into Account the Viscoelastic Material Behavior. Ph.D. Thesis, Montanuniversität Leoben, Leoben, Austria, 2020. [Google Scholar]
- ISO 289-1:2015. Rubber, Unvulcanized—Determinations Using a Shearing-Disc Viscometer—Part 1: Determination of Mooney Viscosity, 4th ed.; International Organization for Standardization: Geneva, Switzerland, 2015. [Google Scholar]
- Datasheet PERBUNAN® 3965 F; Arlanxeo Deutschland GmbH: Dormagen, Germany, 2019.
- Binding, D.M. An approximate analysis for contraction and converging flows. J. Non-Newton. Fluid Mech. 1988, 27, 173–189. [Google Scholar] [CrossRef]
- Fasching, M. Robust Processing in Rubber Injection Molding Using Advanced Simulation Methods and Material Data. Ph.D. Thesis, Montanuniversität Leoben, Leoben, Austria, 2015. [Google Scholar]
- Hatzikiriakos, S.G. Wall slip of molten polymers. Prog. Polym. Sci. 2012, 37, 624–643. [Google Scholar] [CrossRef]
- Mooney, M. Explicit Formulas for Slip and Fluidity. J. Rheol. 1931, 2, 210–222. [Google Scholar] [CrossRef]
- Cox, W.P.; Merz, E.H. Correlation of dynamic and steady flow viscosities. J. Polym. Sci. 1958, 28, 619–622. [Google Scholar] [CrossRef]
- Bagley, E.B. End Corrections in the Capillary Flow of Polyethylene. J. Appl. Phys. 1957, 28, 624–627. [Google Scholar] [CrossRef]
- Maklad, O.; Poole, R.J. A review of the second normal-stress difference; its importance in various flows, measurement techniques, results for various complex fluids and theoretical predictions. J. Non-Newton. Fluid Mech. 2021, 292, 104522. [Google Scholar] [CrossRef]
- Sentmanat, M.L. Miniature universal testing platform: From extensional melt rheology to solid-state deformation behavior. Rheol. Acta 2004, 43, 657–669. [Google Scholar] [CrossRef]
- Meißner, J. Rheometer zur Untersuchung der deformationsmechanischen Eigenschaften von Kunststoff-Schmelzen unter definierter Zugbeanspruchung. Rheol. Acta 1969, 8, 78–88. [Google Scholar] [CrossRef]
- Meissner, J.; Hostettler, J. A new elongational rheometer for polymer melts and other highly viscoelastic liquids. Rheol. Acta 1994, 33, 1–21. [Google Scholar] [CrossRef]
- Münstedt, H. New Universal Extensional Rheometer for Polymer Melts. Measurements on a Polystyrene Sample. J. Rheol. 1979, 23, 421–436. [Google Scholar] [CrossRef]
- Luo, X.-L.; Tanner, R.I. Finite element simulation of long and short circular die extrusion experiments using integral models. Int. J. Numer. Methods Eng. 1988, 25, 9–22. [Google Scholar] [CrossRef]









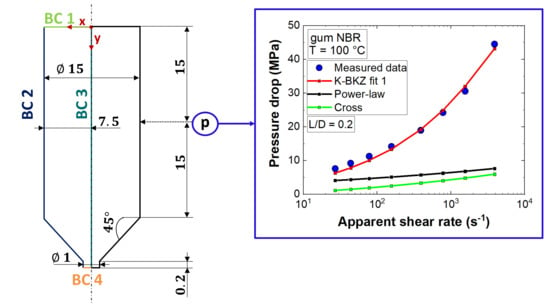
| BC | Description |
|---|---|
| BC 1 | Fully developed velocity profile (inlet) |
| BC 2 | Normal and tangential velocities are zero (no slip at the wall) |
| BC 3 | Tangential force and normal velocity are zero (axis of symmetry) |
| BC 4 | Normal force and tangential velocity are zero (viscous outlet) |
| BC 4 | Normal and tangential forces are zero “zero force BC” (viscoelastic outlet) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stieger, S.; Mitsoulis, E.; Walluch, M.; Ebner, C.; Kerschbaumer, R.C.; Haselmann, M.; Mostafaiyan, M.; Kämpfe, M.; Kühnert, I.; Wießner, S.; et al. On the Influence of Viscoelastic Modeling in Fluid Flow Simulations of Gum Acrylonitrile Butadiene Rubber. Polymers 2021, 13, 2323. https://doi.org/10.3390/polym13142323
Stieger S, Mitsoulis E, Walluch M, Ebner C, Kerschbaumer RC, Haselmann M, Mostafaiyan M, Kämpfe M, Kühnert I, Wießner S, et al. On the Influence of Viscoelastic Modeling in Fluid Flow Simulations of Gum Acrylonitrile Butadiene Rubber. Polymers. 2021; 13(14):2323. https://doi.org/10.3390/polym13142323
Chicago/Turabian StyleStieger, Sebastian, Evan Mitsoulis, Matthias Walluch, Catharina Ebner, Roman Christopher Kerschbaumer, Matthias Haselmann, Mehdi Mostafaiyan, Markus Kämpfe, Ines Kühnert, Sven Wießner, and et al. 2021. "On the Influence of Viscoelastic Modeling in Fluid Flow Simulations of Gum Acrylonitrile Butadiene Rubber" Polymers 13, no. 14: 2323. https://doi.org/10.3390/polym13142323
APA StyleStieger, S., Mitsoulis, E., Walluch, M., Ebner, C., Kerschbaumer, R. C., Haselmann, M., Mostafaiyan, M., Kämpfe, M., Kühnert, I., Wießner, S., & Friesenbichler, W. (2021). On the Influence of Viscoelastic Modeling in Fluid Flow Simulations of Gum Acrylonitrile Butadiene Rubber. Polymers, 13(14), 2323. https://doi.org/10.3390/polym13142323