Heat Transfer Modeling of Oriented Sorghum Fibers Reinforced High-Density Polyethylene Film Composites during Hot-Pressing
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Governing Equations
2.3. Testing and Simulation of HDPE Heat Capacity
2.4. Material Properties
2.4.1. Heat Capacity of Sorghum Fiber and Air
2.4.2. Thermal Conductivity
2.5. Numerical Solution
2.6. Experimental Evaluation of Heat Transfer
3. Results and Discussion
3.1. Heat Capacity and Heat Fusion of HDPE
3.2. Heat Transfer Simulation of Pure HDPE
3.3. Effects of Moisture Content on Heat Transfer
3.4. Effects of Mat Density on Heat Transfer
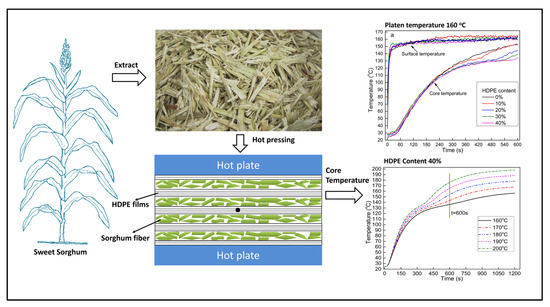
3.5. Effect of HDPE Content on Heat Transfer
3.6. Temperature Distribution Prediction
3.7. Comparison of Experimental Results with the Model Prediction
3.8. Optimization of Hot-Press Parameters
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Friedrich, D. Thermoplastic Moulding of Wood-Polymer Composites (WPC): A Review on Physical and Mechanical Behaviour under Hot-Pressing Technique. Compos. Struct. 2021, 262, 113649. [Google Scholar] [CrossRef]
- Qi, C.; Yadama, V.; Guo, K.; Wolcott, M.P. Preparation and Properties of Oriented Sorghum-Thermoplastic Composites Using Flat Hot-Pressing Technology. J. Reinf. Plast. Compos. 2015, 34, 1241–1252. [Google Scholar] [CrossRef]
- Qi, C.; Yadama, V.; Guo, K.; Wolcott, M.P. Thermal Stability Evaluation of Sweet Sorghum Fiber and Degradation Simulation during Hot Pressing of Sweet Sorghum-Thermoplastic Composite Panels. Ind. Crop. Prod. 2015, 69, 335–343. [Google Scholar] [CrossRef]
- Qi, C.; Yadama, V.; Guo, K.; Wolcott, M.P. Thermal Conductivity of Sorghum and Sorghum-Thermoplastic Composite Panels. Ind. Crop. Prod. 2013, 45, 455–460. [Google Scholar] [CrossRef]
- Stanish, M.A.; Schajer, G.S.; Kayihan, F. A Mathematical Model of Drying for Hygroscopic Porous Media. AiChE J. 1986, 32, 1301–1311. [Google Scholar] [CrossRef]
- Zombori, B.G.; Kamke, F.A.; Watson, L.T. Simulation of the Internal Conditions during the Hot-Pressing Process. Wood Fiber Sci. 2003, 35, 2–23. [Google Scholar]
- Dai, C.; Yu, C. Heat and Mass Transfer in Wood Composite Panels during Hot-Pressing: Part I. A Physical-Mathematical Model. Wood Fiber Sci. 2004, 36, 585–597. [Google Scholar]
- Erchiqui, F.; Kaddami, H.; Dituba-Ngoma, G.; Slaoui-Hasnaoui, F. Comparative Study of the Use of Infrared and Microwave Heating Modes for the Thermoforming of Wood-Plastic Composite Sheets. Int. J. Heat Mass Transf. 2020, 158, 119996. [Google Scholar] [CrossRef]
- Kot, V.A. Solution of the Classical Stefan Problem: Neumann Condition. J. Eng. Phys. Thermophys. 2017, 90, 889–917. [Google Scholar] [CrossRef]
- Khan, S.A.; Girard, P.; Bhuiyan, N.; Thomson, V. Improved Mathematical Modeling for the Sheet Reheat Phase during Thermoforming. Polym. Eng. Sci. 2012, 52, 625–636. [Google Scholar] [CrossRef]
- Nedjar, B. An Enthalpy-Based Finite Element Method for Nonlinear Heat Problems Involving Phase Change. Comput. Struct. 2002, 80, 9–21. [Google Scholar] [CrossRef]
- Mantell, S.C.; Springer, G.S. Manufacturing Process Models for Thermoplastic Composites. J. Compos. Mater. 1992, 26, 2348–2377. [Google Scholar] [CrossRef]
- Xiong, H.; Hamila, N.; Boisse, P. Consolidation Modeling during Thermoforming of Thermoplastic Composite Prepregs. Materials 2019, 12, 2853. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Woo, M.W.; Wong, P.; Tang, Y.; Triacca, V.; Gloor, P.E.; Hrymak, A.N.; Hamielec, A.E. Melting Behavior and Thermal Properties of High Density Polythylene. Polym. Eng. Sci. 1995, 35, 151–156. [Google Scholar] [CrossRef]
- Thoemen, H.; Humphrey, P.E. Modeling the Continuous Pressing Process for Wood-Based Composites. Wood Fiber Sci. 2003, 35, 456–468. [Google Scholar]
- ASTM E1269-11. Standard Test Method for Determining Specific Heat Capacity by Differential Scanning Calorimetry; ASTM International: West Conshohocken, PA, USA, 2018. [Google Scholar]
- Ivanovic, M.; Svicevic, M.; Savovic, S. Numerical Solution of Stefan Problem with Variable Space Grid Method Based on Mixed Finite Element/Finite Difference Approach. Int. J. Numer. Methods Heat Fluid Flow 2017, 27, 2682–2695. [Google Scholar] [CrossRef]
- Qi, C. Fabrication of Oriented Biomass-High Density Polyethylene Composites Using Hot Pressing Process and Its Molding Mechanism. Ph.D. Thesis, Northwest A & F University, Yangling, China, 2013. [Google Scholar]
- Sotomayor, M.E.; Krupa, I.; Várez, A.; Levenfeld, B. Thermal and Mechanical Characterization of Injection Moulded High Density Polyethylene/Paraffin Wax Blends as Phase Change Materials. Renew. Energy 2014, 68, 140–145. [Google Scholar] [CrossRef]
- Oh, D.W. Thermal Characterisation of High Density Polyethylene with Multi-Walled Carbon Nanotube. Int. J. Nanotechnol. 2018, 15, 747–752. [Google Scholar] [CrossRef]
- Li, X.; Tabil, L.G.; Oguocha, I.N.; Panigrahi, S. Thermal Diffusivity, Thermal Conductivity, and Specific Heat of Flax Fiber-HDPE Biocomposites at Processing Temperatures. Compos. Sci. Technol. 2008, 68, 1753–1758. [Google Scholar] [CrossRef]










| Parameters | Symbols | Values | Unit |
|---|---|---|---|
| Specific heat capacity of air | 1000 | J/(kg·K) | |
| Density of sorghum fiber cell wall | 1500 | kg/m3 | |
| Density of high-density polyethylene | 940 | kg/m3 | |
| Air density | 1.225 | kg/m3 | |
| Thermal conductivity of HDPE | 0.44 | W/(m·K) | |
| Mat thickness | H | 0.015 | m |
| Variables | Values | Fixed Parameters | Platen Temperature |
|---|---|---|---|
| HDPE content | 0, 10, 20, 30, 40% | Target mat density was 0.9 g/cm3, 3% moisture content of sorghum fiber | 160 °C |
| Mat density | 0.7, 0.8, 0.9, 1.0 g/cm3 | 10% HDPE, 3% moisture content of sorghum fiber | |
| Sorghum fiber moisture content | 3, 6, 9, 12% | 10% HDPE, target mat density was 0.9 g/cm3 |
| Hot-Press Temperature (°C) | Hot-Pressing Duration (s) | ||||
|---|---|---|---|---|---|
| No HDPE | 10% HDPE | 20% HDPE | 30% HDPE | 40% HDPE | |
| 160 | 645 | 710 | 781 | 861 | 954 |
| 170 | 490 | 533 | 582 | 637 | 702 |
| 180 | 410 | 443 | 480 | 523 | 574 |
| 190 | 360 | 385 | 415 | 451 | 494 |
| 200 | 323 | 344 | 370 | 400 | 437 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Qi, C.; Wang, J.; Yadama, V. Heat Transfer Modeling of Oriented Sorghum Fibers Reinforced High-Density Polyethylene Film Composites during Hot-Pressing. Polymers 2021, 13, 3631. https://doi.org/10.3390/polym13213631
Qi C, Wang J, Yadama V. Heat Transfer Modeling of Oriented Sorghum Fibers Reinforced High-Density Polyethylene Film Composites during Hot-Pressing. Polymers. 2021; 13(21):3631. https://doi.org/10.3390/polym13213631
Chicago/Turabian StyleQi, Chusheng, Jinyue Wang, and Vikram Yadama. 2021. "Heat Transfer Modeling of Oriented Sorghum Fibers Reinforced High-Density Polyethylene Film Composites during Hot-Pressing" Polymers 13, no. 21: 3631. https://doi.org/10.3390/polym13213631
APA StyleQi, C., Wang, J., & Yadama, V. (2021). Heat Transfer Modeling of Oriented Sorghum Fibers Reinforced High-Density Polyethylene Film Composites during Hot-Pressing. Polymers, 13(21), 3631. https://doi.org/10.3390/polym13213631