Reconfigurable Surface Micropatterns Based on the Magnetic Field-Induced Shape Memory Effect in Magnetoactive Elastomers
Abstract
:1. Introduction
2. Materials and Methods
3. Results
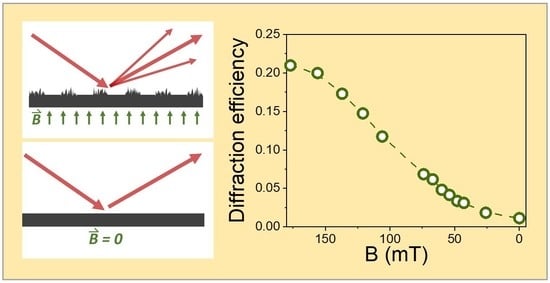
3.1. Experimental Results
3.2. Model of the Optical Diffraction Structure
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Filipcsei, G.; Csetneki, I.; Szilagyi, A.; Zrinyi, M. Magnetic Field-Responsive Smart Polymer Composites. Adv. Polym. Sci. 2007, 206, 137–189. [Google Scholar] [CrossRef]
- Abramchuk, S.; Kramarenko, E.; Stepanov, G.; Nikitin, L.V.; Filipcsei, G.; Khokhlov, A.R.; Zrínyi, M. Novel Highly Elastic Magnetic Materials for Dampers and Seals: Part I. Preparation and Characterization of the Elastic Materials. Polym. Adv. Technol. 2007, 18, 883–890. [Google Scholar] [CrossRef]
- Samal, S.; Škodová, M.; Abate, L.; Blanco, I. Magneto-Rheological Elastomer Composites. A Review. Appl. Sci. 2020, 10, 4899. [Google Scholar] [CrossRef]
- Kang, S.S.; Choi, K.; Nam, J.-D.; Choi, H.J. Magnetorheological Elastomers: Fabrication, Characteristics, and Applications. Materials 2020, 13, 4597. [Google Scholar] [CrossRef]
- Liu, T.; Xu, Y. Magnetorheological elastomers: Materials and applications. In Smart and Functional Soft Materials; Dong, X., Ed.; IntechOpen: London, UK, 2019; pp. 147–180. [Google Scholar] [CrossRef] [Green Version]
- Bastola, A.K.; Paudel, M.; Li, L.; Li, W. Recent Progress of Magnetorheological Elastomers: A Review. Smart Mater. Struct. 2020, 29, 123002. [Google Scholar] [CrossRef]
- Odenbach, S. (Ed.) Magnetic Hybrid-Materials: Multi-Scale Modelling, Synthesis, and Applications; De Gruyter: Berlin, Germany, 2021; ISBN 978-3-11-056963-6. [Google Scholar]
- Díez, A.G.; Tubio, C.R.; Etxebarria, J.G.; Lanceros-Mendez, S. Magnetorheological Elastomer-Based Materials and Devices: State of the Art and Future Perspectives. Adv. Eng. Mater. 2021, 23, 2100240. [Google Scholar] [CrossRef]
- Lee, S.; Yim, C.; Kim, W.; Jeon, S. Magnetorheological Elastomer Films with Tunable Wetting and Adhesion Properties. ACS Appl. Mater. Interfaces 2015, 7, 19853–19856. [Google Scholar] [CrossRef]
- Sorokin, V.V.; Sokolov, B.O.; Stepanov, G.V.; Kramarenko, E.Y. Controllable Hydrophobicity of Magnetoactive Elastomer Coatings. J. Magn. Magn. Mater. 2018, 459, 268–271. [Google Scholar] [CrossRef]
- Nanpo, J.; Kawai, M.; Mitsumata, T. Magnetic-Field Sensitivity for Magnetic Elastomers with Various Elasticities. Chem. Lett. 2016, 45, 785–786. [Google Scholar] [CrossRef]
- Sorokin, V.V.; Belyaeva, I.A.; Shamonin, M.; Kramarenko, E.Y. Magnetorheological Response of Highly Filled Magnetoactive Elastomers from Perspective of Mechanical Energy Density: Fractal Aggregates above the Nanometer Scale? Phys. Rev. E 2017, 95, 062501. [Google Scholar] [CrossRef]
- Belyaeva, I.A.; Kramarenko, E.Y.; Shamonin, M. Magnetodielectric Effect in Magnetoactive Elastomers: Transient Response and Hysteresis. Polymer 2017, 127, 119–128. [Google Scholar] [CrossRef]
- Maman, M.; Ponsinet, V. Wettability of Magnetically Susceptible Surfaces. Langmuir 1999, 15, 259–265. [Google Scholar] [CrossRef]
- Knieling, H.; Richter, R.; Rehberg, I.; Matthies, G.; Lange, A. Growth of Surface Undulations at the Rosensweig Instability. Phys. Rev. E 2008, 76, 066301. [Google Scholar] [CrossRef] [Green Version]
- Psarra, E.; Bodelot, L.; Danas, K. Two-Field Surface Pattern Control via Marginally Stable Magnetorheological Elastomers. Soft Matter 2017, 13, 6576–6584. [Google Scholar] [CrossRef] [Green Version]
- Cvek, M.; Mrlik, M.; Sevcik, J.; Sedlacik, M. Tailoring Performance, Damping, and Surface Properties of Magnetorheological Elastomers via Particle-Grafting Technology. Polymers 2018, 10, 1411. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Sánchez, P.A.; Minina, E.S.; Kantorovich, S.S.; Kramarenko, E.Y. Surface Relief of Magnetoactive Elastomeric Films in a Homogeneous Magnetic Field: Molecular Dynamics Simulations. Soft Matter 2019, 15, 175–189. [Google Scholar] [CrossRef] [Green Version]
- Li, R.; Li, X.; Chen, S.; Wang, X. The Effect of Magnetic Field on Surface Roughness of Magnetorheological Elastomers: A Theoretical Simulation. Proc. SPIE 2018, 10595, 105951J. [Google Scholar] [CrossRef]
- Chen, S.; Dong, S.; Wang, X.; Li, W. Magneto-Induced Surface Morphologies in Magnetorheological Elastomer Films: An Analytical Study. Smart Mater. Struct. 2019, 28, 045016. [Google Scholar] [CrossRef]
- Glavan, G.; Kettl, W.; Brunhuber, A.; Shamonin, M.; Drevenšek-Olenik, I. Effect of Material Composition on Tunable Surface Roughness of Magnetoactive Elastomers. Polymers 2019, 11, 594. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Li, R.; Li, X.; Yang, P.; Liu, J.; Chen, S. The Field-Dependent Surface Roughness of Magnetorheological Elastomer: Numerical Simulation and Experimental Verification. Smart Mater. Struct. 2019, 28, 085018. [Google Scholar] [CrossRef]
- Nadzharyan, T.A.; Stolbov, O.V.; Raikher, Y.L.; Kramarenko, E.Y. Field-Induced Surface Deformation of Magnetoactive Elastomers with Anisometric Fillers: A Single-Particle Model. Soft Matter 2019, 15, 9507–9519. [Google Scholar] [CrossRef] [PubMed]
- Zhou, Y.; Huang, S.; Tian, X. Magnetoresponsive Surfaces for Manipulation of Nonmagnetic Liquids: Design and Applications. Adv. Funct. Mater. 2020, 30, 1906507. [Google Scholar] [CrossRef]
- Glavan, G.; Salamon, P.; Belyaeva, I.A.; Shamonin, M.; Drevenšek-Olenik, I. Tunable Surface Roughness and Wettability of a Soft Magnetoactive Elastomer. J. Appl. Polym. Sci. 2018, 135, 46221. [Google Scholar] [CrossRef]
- Yang, C.; Wu, L.; Li, G. Magnetically Responsive Superhydrophobic Surface: In Situ Reversible Switching of Water Droplet Wettability and Adhesion for Droplet Manipulation. ACS Appl. Mater. Interfaces 2018, 10, 20150–20158. [Google Scholar] [CrossRef] [PubMed]
- Watanabe, M.; Tanaka, Y.; Murakami, D.; Tanaka, M.; Kawai, M.; Mitsumata, T. Optimal Plasticizer Content for Magnetic Elastomers Used for Cell Culture Substrate. Chem. Lett. 2020, 49, 280–283. [Google Scholar] [CrossRef]
- Chen, S.; Zhu, M.; Zhang, Y.; Dong, S.; Wang, X. Magnetic-Responsive Superhydrophobic Surface of Magnetorheological Elastomers Mimicking from Lotus Leaves to Rose Petals. Langmuir 2021, 37, 2312–2321. [Google Scholar] [CrossRef]
- Krahn, J.; Bovero, E.; Menon, C. Magnetic Field Switchable Dry Adhesives. ACS Appl. Mater. Interfaces 2015, 7, 2214–2222. [Google Scholar] [CrossRef]
- Risan, J.; Croll, A.B.; Azarmi, F. Compliance Switching for Adhesion Control. J. Polym. Sci. Part B Polym. Phys. 2015, 53, 48–57. [Google Scholar] [CrossRef]
- Testa, P.; Chappuis, B.; Kistler, S.; Style, R.W.; Heyderman, L.J.; Dufresne, E.R. Switchable Adhesion of Soft Composites Induced by a Magnetic Field. Soft Matter 2020, 16, 5806–5811. [Google Scholar] [CrossRef]
- Li, R.; Wang, D.; Yang, P.; Tang, X.; Liu, J.; Li, X. Improved Magneto-Sensitive Adhesion Property of Magnetorheological Elastomers Modified Using Graphene Nanoplatelets. Ind. Eng. Chem. Res. 2020, 59, 9143–9151. [Google Scholar] [CrossRef]
- Lee, D.-W.; Lee, K.; Lee, C.-H.; Kim, C.-H.; Cho, W.-O. A Study on the Tribological Characteristics of a Magneto-Rheological Elastomer. J. Tribol. 2012, 135, 014501. [Google Scholar] [CrossRef]
- Lian, C.; Lee, K.-H.; Lee, C.-H. Friction and Wear Characteristics of Magneto-Rheological Elastomers Based on Silicone/Polyurethane Hybrid. J. Tribol. 2015, 137, 031607. [Google Scholar] [CrossRef]
- Lian, C.; Lee, K.-H.; Lee, C.-H. Friction and Wear Characteristics of Magnetorheological Elastomer under Vibration Conditions. Tribol. Int. 2016, 98, 292–298. [Google Scholar] [CrossRef]
- Lian, C.; Lee, K.-H.; Lee, C.-H. Effect of Temperature and Relative Humidity on Friction and Wear Properties of Silicone-Based Magnetorheological Elastomer. Tribol. Trans. 2018, 61, 238–246. [Google Scholar] [CrossRef]
- Li, R.; Ren, D.; Wang, X.; Chen, X.; Chen, S.; Wu, X. Tunable Friction Performance of Magneto-Rheological Elastomer Induced by External Magnetic Field. J. Intell. Mater. Syst. Struct. 2018, 29, 160–170. [Google Scholar] [CrossRef]
- Li, R.; Li, X.; Li, Y.; Yang, P.; Liu, J. Experimental and Numerical Study on Surface Roughness of Magnetorheological Elastomer for Controllable Friction. Friction 2020, 8, 917–929. [Google Scholar] [CrossRef] [Green Version]
- Kravanja, G.; Belyaeva, I.; Hribar, L.; Drevensek-Olenik, I.; Jezeršek, M.; Shamonin, M. Tunable Drop Splashing on Magnetoactive Elastomers. Adv. Mater. Interfaces 2021, 8, 2100235. [Google Scholar] [CrossRef]
- Nikitin, L.V.; Stepanov, G.V.; Mironova, L.S.; Gorbunov, A.I. Magnetodeformational Effect and Effect of Shape Memory in Magnetoelastics. J. Magn. Magn. Mater. 2004, 272–276, 2072–2073. [Google Scholar] [CrossRef]
- Stepanov, G.V.; Abramchuk, S.S.; Grishin, D.A.; Nikitin, L.V.; Kramarenko, E.Y.; Khokhlov, A.R. Effect of a Homogeneous Magnetic Field on the Viscoelastic Behavior of Magnetic Elastomers. Polymer 2007, 2, 488–495. [Google Scholar] [CrossRef]
- Stepanov, G.V.; Borin, D.Y.; Raikher, Y.L.; Melenev, P.V.; Perov, N.S. Motion of Ferroparticles inside the Polymeric Matrix in Magnetoactive Elastomers. J. Phys. Condens. Matter 2008, 20, 204121. [Google Scholar] [CrossRef]
- Melenev, P.V.; Raikher, Y.L.; Rusakov, V.V.; Stepanov, G.V. Field-Induced Plasticity of Soft Magnetic Elastomers. J. Phys. Conf. Ser. 2009, 149, 012094. [Google Scholar] [CrossRef] [Green Version]
- Melenev, P.; Raikher, Y.; Stepanov, G.; Rusakov, V.; Polygalova, L. Modeling of the Field-Induced Plasticity of Soft Magnetic Elastomers. J. Intell. Mater. Syst. Struct. 2011, 22, 531–538. [Google Scholar] [CrossRef]
- Stepanov, G.; Kramarenko, E.; Semerenko, D. Magnetodeformational Effect of the Magnetoactive Elastomer and Its Possible Applications. J. Phys. Conf. Ser. 2013, 412, 2031. [Google Scholar] [CrossRef]
- Stolbov, O.; Raikher, Y. Mesostructural Origin of the Field-Induced Pseudo-Plasticity Effect in a Soft Magnetic Elastomer. IOP Conf. Ser. Mater. Sci. Eng. 2019, 581, 012003. [Google Scholar] [CrossRef]
- Shamonin, M.; Kramarenko, E.Y. Chapter 7—Highly Responsive Magnetoactive Elastomers. In Novel Magnetic Nanostructures; Elsevier: Amsterdam, The Netherlands, 2018. [Google Scholar] [CrossRef]
- Testa, P.; Style, R.W.; Cui, J.; Donnelly, C.; Borisova, E.; Derlet, P.M.; Dufresne, E.R.; Heyderman, L.J. Magnetically Addressable Shape-Memory and Stiffening in a Composite Elastomer. Adv. Mater. 2019, 31, e1900561. [Google Scholar] [CrossRef] [PubMed]
- Prem, N.; Sindersberger, D.; Striegl, B.; Böhm, V.; Monkman, G.J. Shape Memory Effects Using Magnetoactive Boron−Organo−Silicon Oxide Polymers. Macromol. Chem. Phys. 2020, 221, 2000149. [Google Scholar] [CrossRef]
- Saveliev, D.V.; Belyaeva, I.A.; Chashin, D.V.; Fetisov, L.Y.; Romeis, D.; Kettl, W.; Kramarenko, E.Y.; Saphiannikova, M.; Stepanov, G.V.; Shamonin, M. Giant Extensional Strain of Magnetoactive Elastomeric Cylinders in Uniform Magnetic Fields. Materials 2020, 13, 3297. [Google Scholar] [CrossRef]
- Fowles, G.R. Introduction to Modern Optics; Holt, Rinehart and Winston: New York, NY, USA, 1968. [Google Scholar]
- Schueller, O.J.A.; Duffy, D.C.; Rogers, J.A.; Brittain, S.T.; Whitesides, G.M. Reconfigurable Diffraction Gratings Based on Elastomeric Microfluidic Devices. Sens. Actuators A Phys. 1999, 78, 149–159. [Google Scholar] [CrossRef]
- Hosokawa, K.; Hanada, K.; Maeda, R. A Polydimethylsiloxane (PDMS) Deformable Diffraction Grating for Monitoring of Local Pressure in Microfluidic Devices. J. Micromech. Microeng. 2001, 12, 1. [Google Scholar] [CrossRef]
- Yu, J.Q.; Yang, Y.; Liu, A.Q.; Chin, L.K.; Zhang, X.M. Microfluidic Droplet Grating for Reconfigurable Optical Diffraction. Opt. Lett. 2010, 35, 1890–1892. [Google Scholar] [CrossRef] [Green Version]
- Grzybowski, B.A.; Qin, D.; Whitesides, G.M. Beam Redirection and Frequency Filtering with Transparent Elastomeric Diffractive Elements. Appl. Opt. 1999, 38, 2997–3002. [Google Scholar] [CrossRef] [PubMed]
- Grzybowski, B.; Qin, D.; Haag, R.; Whitesides, G.M. Elastomeric Optical Elements with Deformable Surface Topographies: Applications to Force Measurements, Tunable Light Transmission and Light Focusing. Sens. Actuators A Phys. 2000, 86, 81–85. [Google Scholar] [CrossRef]
- Guglielmelli, A.; Nemati, S.; Vasdekis, A.E.; Sio, L.D. Stimuli Responsive Diffraction Gratings in Soft-Composite Materials. J. Phys. D Appl. Phys. 2018, 52, 053001. [Google Scholar] [CrossRef]
- Chen, C.-Y.; Tsai, T.-R.; Pan, C.-L.; Pan, R.-P. Room Temperature Terahertz Phase Shifter Based on Magnetically Controlled Birefringence in Liquid Crystals. Appl. Phys. Lett. 2003, 83, 4497–4499. [Google Scholar] [CrossRef] [Green Version]
- Chen, C.-Y.; Hsieh, C.-F.; Lin, Y.-F.; Pan, R.-P.; Pan, C.-L. Magnetically Tunable Room-Temperature 2π Liquid Crystal Terahertz Phase Shifter. Opt. Express 2004, 12, 2625–2630. [Google Scholar] [CrossRef] [PubMed]
- Zhang, L.; Fan, Y.-X.; Liu, H.; Han, X.; Lu, W.-Q.; Tao, Z.-Y. A Magnetically Tunable Non-Bragg Defect Mode in a Corrugated Waveguide Filled with Liquid Crystals. Phys. Lett. A 2018, 382, 1000–1005. [Google Scholar] [CrossRef]
- Bošnjaković, D.; Sebastián, N.; Drevenšek-Olenik, I. Magnetically Tunable Liquid Crystal-Based Optical Diffraction Gratings. Polymers 2020, 12, 2355. [Google Scholar] [CrossRef] [PubMed]
- Tippets, C.A.; Li, Q.; Fu, Y.; Donev, E.U.; Zhou, J.; Turner, S.A.; Jackson, A.-M.S.; Sheares Ashby, V.; Sheiko, S.S.; Lopez, R. Dynamic Optical Gratings Accessed by Reversible Shape Memory. ACS Appl. Mater. Interfaces 2015, 7, 14288–14293. [Google Scholar] [CrossRef]
- Li, Z.; Sun, R.; Rahman, M.A.; Feng, J.; Olah, A.; Baer, E. Scaling Effect on the Optical Properties of Patterned Nano-Layered Shape Memory Films. Polymer 2019, 167, 182–192. [Google Scholar] [CrossRef]
- Zhang, F.; Xia, Y.; Liu, Y.; Leng, J. Nano/Microstructures of Shape Memory Polymers: From Materials to Applications. Nanoscale Horiz. 2020, 5, 1155–1173. [Google Scholar] [CrossRef]
- Schauer, S.; Baumberg, J.J.; Hölscher, H.; Smoukov, S.K. Tuning of Structural Colors Like a Chameleon Enabled by Shape-Memory Polymers. Macromol. Rapid Commun. 2018, 39, 1800518. [Google Scholar] [CrossRef] [PubMed]
- Wang, Y.; Zhai, Y.; Villada, A.; David, S.N.; Yin, X.; Xiao, J. Programmable Localized Wrinkling of Thin Films on Shape Memory Polymers with Application in Nonuniform Optical Gratings. App. Phys. Lett. 2018, 112, 251603. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Lovšin, M.; Brandl, D.; Glavan, G.; Belyaeva, I.A.; Cmok, L.; Čoga, L.; Kalin, M.; Shamonin, M.; Drevenšek-Olenik, I. Reconfigurable Surface Micropatterns Based on the Magnetic Field-Induced Shape Memory Effect in Magnetoactive Elastomers. Polymers 2021, 13, 4422. https://doi.org/10.3390/polym13244422
Lovšin M, Brandl D, Glavan G, Belyaeva IA, Cmok L, Čoga L, Kalin M, Shamonin M, Drevenšek-Olenik I. Reconfigurable Surface Micropatterns Based on the Magnetic Field-Induced Shape Memory Effect in Magnetoactive Elastomers. Polymers. 2021; 13(24):4422. https://doi.org/10.3390/polym13244422
Chicago/Turabian StyleLovšin, Matija, Dominik Brandl, Gašper Glavan, Inna A. Belyaeva, Luka Cmok, Lucija Čoga, Mitjan Kalin, Mikhail Shamonin, and Irena Drevenšek-Olenik. 2021. "Reconfigurable Surface Micropatterns Based on the Magnetic Field-Induced Shape Memory Effect in Magnetoactive Elastomers" Polymers 13, no. 24: 4422. https://doi.org/10.3390/polym13244422
APA StyleLovšin, M., Brandl, D., Glavan, G., Belyaeva, I. A., Cmok, L., Čoga, L., Kalin, M., Shamonin, M., & Drevenšek-Olenik, I. (2021). Reconfigurable Surface Micropatterns Based on the Magnetic Field-Induced Shape Memory Effect in Magnetoactive Elastomers. Polymers, 13(24), 4422. https://doi.org/10.3390/polym13244422