Magnetorheological Response for Magnetic Elastomers Containing Carbonyl Iron Particles Coated with Poly(methyl methacrylate)
Abstract
:1. Introduction
2. Experimental procedures
2.1. Synthesis of Magnetic Elastomers and Gels
2.2. Dynamic Viscoelastic Measurement
2.3. SEM Observation
2.4. FT-IR Spectroscopy
2.5. Thermogravimetric Analysis
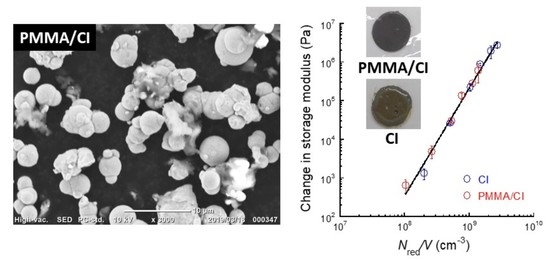
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kose, O.; Boott, C.E.; Hamad, W.Y.; MacLachlan, M.J. Stimuli-Responsive Anisotropic Materials Based on Unidirectional Organization of Cellulose Nanocrystals in an Elastomers. Macromolecules 2019, 52, 5317–5324. [Google Scholar] [CrossRef]
- Du, J.; Zhang, Z.L.; Liu, D.B.; Ren, T.B.; Wan, D.C.; Pu, H.T. Triple-stimuli responsive shape memory effect of novel polyolefin elastomer/lauric acid/carbon black. Compos. Sci. Tech. 2019, 169, 45–51. [Google Scholar] [CrossRef]
- Kaiser, S.; Radl, S.V.; Manhart, J.; Ayalur-Karunakaran, S.; Griesser, T.; Moser, A.; Ganser, C.; Teichert, C.; Kern, W.; Schlogl, S. Switching “on” and “off” the adhesion in stimuli-responsive elastomers. Soft Matter 2018, 14, 2547–2559. [Google Scholar] [CrossRef] [PubMed]
- Amaral, A.J.R.; Pasparakis, G. Stimuli responsive self-healing polymers: Gels, elastomers and membranes. Polym. Chem. 2017, 8, 6464–6484. [Google Scholar] [CrossRef] [Green Version]
- Wang, M.; Sayed, S.M.; Guo, L.X.; Lin, B.P.; Zhang, X.Q.; Sun, Y.; Yang, H. Multi-Stimuli Responsive Carbon Nanotube Incorporated Polysiloxane Azobenzene Liquid Crystalline Elastomer Composites. Macromolcules 2016, 49, 663–671. [Google Scholar] [CrossRef]
- Qi, S.; Fu, J.; Xie, Y.P.; Li, Y.P.; Gan, R.Y.; Yu, M. Versatile magnetorheological plastomer with 3D printability, switchable mechanics, shape memory, and self-healing capacity. Compos. Sci. Tech. 2019, 183, 107817. [Google Scholar] [CrossRef]
- Kim, J.G.; Park, J.E.; Won, S.; Jeon, J.; Wie, J.J. Contactless Manipulation of Soft Robots. Materials 2019, 12, 3065. [Google Scholar] [CrossRef] [Green Version]
- Ditter, D.; Bluemler, P.; Klockner, B.; Hilgert, J.; Zentel, R. Microfluidic Synthesis of Liquid Crystalline Elastomer Particle Transport Systems which Can Be Remote-Controlled. Adv. Funct. Mater. 2019, 29, 1902454. [Google Scholar] [CrossRef]
- Saveliev, D.V.; Belyaeva, I.A.; Chashin, D.V.; Fetisov, L.Y.; Romeis, D.; Kettl, W.; Kramarenko, E.Y.; Saphiannikova, M.; Stepanov, G.V.; Shamonin, M. Giant Extensional Strain of Magnetoactive Elastomeric Cylinders in Uniform Magnetic Fields. Materials 2020, 13, 3297. [Google Scholar] [CrossRef]
- Kuznetsova, I.E.; Kolesov, V.V.; Fionov, A.S.; Kramarenko, E.Y.; Stepanov, G.V.; Mikheev, M.G.; Verona, E.; Solodov, I. Magnetoactive elastomers with controllable radio-absorbing properties. Mater. Today Commun. 2019, 21, 100610. [Google Scholar] [CrossRef]
- Mitsumata, T.; Ohori, S.; Chiba, N.; Kawai, M. Enhancement of magnetoelastic behavior of bimodal magnetic elastomers by stress transfer via nonmagnetic particles. Soft Matter 2013, 9, 10108–10116. [Google Scholar] [CrossRef]
- Nagashima, K.; Kanauchi, S.; Kawai, M.; Mitsumata, T.; Tamesue, S.; Yamauchi, T. Nonmagnetic particles enhance magnetoelastic response of magnetic elastomers. J. Appl. Phys. 2015, 118, 024903. [Google Scholar] [CrossRef]
- Nanpo, J.; Nagashima, K.; Umehara, Y.; Kawai, M.; Mitsumata, T. Magnetic-Field Sensitivity of Storage Modulus for Bimodal Magnetic Elastomers. J. Phys. Chem. B 2016, 120, 12993–13000. [Google Scholar] [CrossRef] [PubMed]
- Umehara, Y.; Yamanaga, Y.; Akama, S.; Kato, S.; Kamoshita, S.; Kawai, M.; Mitsumata, T. Railway Actuator Made of Magnetic Elastomers and Driven by a Magnetic Field. Polymers 2018, 10, 1351. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kobayashi, Y.; Akama, S.; Ohori, S.; Kawai, M.; Mitsumata, T. Magnetic Elastomers with Smart Variable Elasticity Mimetic to Sea Cucumber. Biomimetics 2019, 4, 68. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watanabe, M.; Ikeda, J.; Takeda, Y.; Kawai, M.; Mitsumata, T. Effect of Sonication Time on Magnetorheological Effect for Monomodal Magnetic Elastomers. Gels 2018, 4, 49. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Watanabe, M.; Takeda, Y.; Maruyama, T.; Ikeda, J.; Kawai, M.; Mitsumata, T. Chain Structure in a Cross-Linked Polyurethane Magnetic Elastomer Under a Magnetic Field. Int. J. Mol. Sci. 2019, 20, 2879. [Google Scholar] [CrossRef] [Green Version]
- Ge, L.; Gong, X.; Fan, Y.; Xuan, S. Preparation and mechanical properties of the magnetorheological elastomer based on natural rubber/rosin glycerin hybrid matrix. Smart Mater. Struct. 2013, 22, 115029. [Google Scholar] [CrossRef] [Green Version]
- Yuan, F.; Jiao, W.; Fan, Y.; Liu, W.; Xu, Z.; Wang, R. Surface modification and magnetic alignment of hexagonal boron nitride nanosheets for highly thermally conductive composites. RSC Adv. 2017, 7, 43380–43389. [Google Scholar] [CrossRef] [Green Version]
- Ikeda, J.; Takahashi, D.; Watanabe, M.; Kawai, M.; Mitsumata, T. Particle Size in Secondary Particle and Magnetic Response for Carrageenan Magnetic Hydrogels. Gels 2019, 5, 39. [Google Scholar] [CrossRef] [Green Version]
- Fang, F.F.; Choi, H.J.; Seo, Y. Sequential Coating of Magnetic Carbonyl iron Particles with Polystyrene and Multiwalled Carbon Nanotubes and Its Effect on Their Magnetorheology. ACS Appl. Mater. Interfaces 2010, 2, 54–60. [Google Scholar] [CrossRef] [PubMed]
- Choi, J.S.; Park, B.J.; Cho, M.S.; Choi, H.J. Preparation and magnetorheological characteristics of polymer coated carbonyl iron suspensions. J. Mag. Mag. Mater. 2006, 304, e374–e376. [Google Scholar] [CrossRef]
- Liu, Y.D.; Choi, H.J. Carbon nanotube-coated silicated soft magnetic carbonyl iron microspheres and their magnetorheology. J. Appl. Phys. 2012, 111, 07B502. [Google Scholar] [CrossRef]
- An, J.S.; Kwon, S.H.; Choi, H.J.; Jung, J.H.; Kim, Y.G. Modified silane-coated carbonyl iron/natural rubber composite elastomer and its magnetorheological performance. Compos. Struct. 2017, 160, 1020–1026. [Google Scholar] [CrossRef]
- Liu, Y.D.; Choi, H.J. Magnetorheology of core–shell typed dual-coated carbonyl iron particle fabricated by a sol–gel and self-assembly process. Mater. Res. Bull. 2015, 69, 92–97. [Google Scholar] [CrossRef]
- Min, T.H.; Choi, H.J.; Kim, N.-H.; Park, K.; You, C.-Y. Effects of surface treatment on magnetic carbonyl iron/polyaniline microspheres and their magnetorheological study, Colloids and Surfaces A: Physicochem. Eng. Asp. 2017, 48, 531. [Google Scholar]
- Guth, E.; Simba, R. Untersuchungen über die Viskosität von Suspensionen und Lösungen. 3. Über die Viskosität von Kugelsuspensionen. Kolloid Zeit. 1936, 74, 266–275. [Google Scholar] [CrossRef]
- Jeon, J.; Park, J.E.; Park, S.J.; Won, S.; Zhao, H.; Kim, S.; Shim, B.S.; Urbas, A.; Hart, J.; Ku, Z.; et al. Shape-Programmed Fabrication and Actuation of Magnetically Active Micropost Arrays, ACS Appl. Mater. Interfaces 2020, 12, 17113–17120. [Google Scholar]
- Park, J.E.; Jeon, J.; Park, S.J.; Won, S.; Ku, Z.; Wie, J.J. Enhancement of Magneto-Mechanical Actuation of Micropillar Arrays by Anisotropic Stress Distribution. Small 2020, 16, 2003179. [Google Scholar] [CrossRef]
- Kang, S.S.; Choi, K.; Nam, J.-D.; Choi, H.J. Magnetorheological Elastomers: Fabrication, Characteristics, and Applications. Materials 2020, 13, 4597. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Takahashi, D.; Sainath, A.V.S.; Ikeda, J.; Budpud, K.; Kaneko, T.; Kawai, M.; Mitsumata, T. Magnetorheological Response for Magnetic Elastomers Containing Carbonyl Iron Particles Coated with Poly(methyl methacrylate). Polymers 2021, 13, 335. https://doi.org/10.3390/polym13030335
Takahashi D, Sainath AVS, Ikeda J, Budpud K, Kaneko T, Kawai M, Mitsumata T. Magnetorheological Response for Magnetic Elastomers Containing Carbonyl Iron Particles Coated with Poly(methyl methacrylate). Polymers. 2021; 13(3):335. https://doi.org/10.3390/polym13030335
Chicago/Turabian StyleTakahashi, Daichi, Annadanam Venkata Sesha Sainath, Junko Ikeda, Kulisara Budpud, Tatsuo Kaneko, Mika Kawai, and Tetsu Mitsumata. 2021. "Magnetorheological Response for Magnetic Elastomers Containing Carbonyl Iron Particles Coated with Poly(methyl methacrylate)" Polymers 13, no. 3: 335. https://doi.org/10.3390/polym13030335
APA StyleTakahashi, D., Sainath, A. V. S., Ikeda, J., Budpud, K., Kaneko, T., Kawai, M., & Mitsumata, T. (2021). Magnetorheological Response for Magnetic Elastomers Containing Carbonyl Iron Particles Coated with Poly(methyl methacrylate). Polymers, 13(3), 335. https://doi.org/10.3390/polym13030335