Insights into the Bead Fusion Mechanism of Expanded Polybutylene Terephthalate (E-PBT)
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
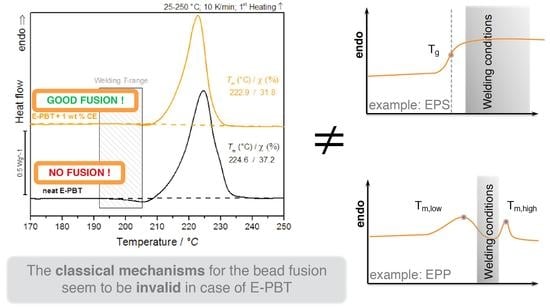
3.1. Crystalline Propertis of PBT Bead Foams
3.2. Non-Isothermal Crystallization Kinetics
3.3. Isothermal Hot-Crystallization Kinetics
3.4. Isothermal Cold-Crystallization Kinetics
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Raps, D.; Hossieny, N.; Park, C.B.; Altstädt, V. Past and present developments in polymer bead foams and bead foaming technology. Polymer 2015, 56, 5–19. [Google Scholar] [CrossRef]
- Eaves, D. Handbook of Polymer Foams; Rapra Technology: Shrewsbury, UK, 2004. [Google Scholar]
- Britton, R. Update on Mouldable Particle Foam Technology; Rapra Technology: Shrewsbury, UK, 2009. [Google Scholar]
- Weingart, N.; Raps, D.; Kuhnigk, J.; Klein, A.; Altstädt, V. Expanded Polycarbonate (EPC)—A New Generation of High-Temperature Engineering Bead Foams. Polymers (Basel) 2020, 12, 2314. [Google Scholar] [CrossRef]
- Mills, N. Polymer Foams Handbook Engineering and Biomechanics Applications and Design; Guide Butterworth-Heinemann: Boston, MA, USA, 2007. [Google Scholar]
- Noordegraaf, J.; Kuijstermans, F.P.A.; De Jong, J.P.M. Particulate, Expandable Polymer, Method for Producing Particulate Expandable Polymer, as well as a Special Use of the Obtained Foam Material. U.S. Patent Application No. 13/122,960, 14 April 2011. [Google Scholar]
- Trassl, C.; Altstädt, V. Particle foams: Future materials for lightweight construction and design. Kunstst. Int. 2014, 2, 73–76. [Google Scholar]
- Guo, Y.; Hossieny, N.; Chu, R.K.M.; Park, C.B.; Zhou, N. Critical processing parameters for foamed bead manufacturing in a lab-scale autoclave system. Chem. Eng. J. 2013, 214, 180–188. [Google Scholar] [CrossRef]
- Nofar, M.; Guo, Y.; Park, C.B. Double crystal melting peak generation for expanded polypropylene bead foam manufacturing. Ind. Eng. Chem. Res. 2013, 52, 2297–2303. [Google Scholar] [CrossRef]
- Spies, P.; Braun, F.; Schips, C.; Prissok, F.; Gutmann, P.; Hahn, K.; Schmied, B. Polyurethane-Based Expandable Polymer Particles. US Patent 9447249, 20 September 2016. [Google Scholar]
- Prissok, F. Foams Based on Thermoplastic Polyurethans. US Patent 9884947B2, 2 September 2010. [Google Scholar]
- Nofar, M.; Batı, B.; Küçük, E.B.; Jalali, A. Effect of soft segment molecular weight on the microcellular foaming behavior of TPU using supercritical CO2. J. Supercrit. Fluids 2020, 160, 4816. [Google Scholar] [CrossRef]
- Park, C.B.; Nofar, M. A Method for the Preparation of PLA Bead Foams. WO Patent WO2014158014 A1, 28 March 2013. [Google Scholar]
- Nofar, M.; Ameli, A.; Park, C.B. Development of polylactide bead foams with double crystal melting peaks. Polymer 2015, 69, 83–94. [Google Scholar] [CrossRef]
- Nofar, M.; Ameli, A.; Park, C.B. A novel technology to manufacture biodegradable polylactide bead foam products. Mater. Des. 2015, 83, 413–421. [Google Scholar] [CrossRef]
- Standau, T.; Zhao, C.; Castellón, S.M.; Bonten, C.; Altstädt, V. Chemical modification and foam processing of polylactide (PLA). Polymers (Basel) 2019, 11, 306. [Google Scholar] [CrossRef] [Green Version]
- Richter, T.; Schwarz-Barac, S.; Bernhard, K.; Liebl, I.; Schnabel, M.; Schweitzer, S.; Poppe, D.; Vorholz, J. Bead Polymer for Producing PMI Foams. U.S. Patent Application 14/765,472, 17 December 2015. [Google Scholar]
- Strasser, J.P. Process for Producing PET Pellets, and PET Pellets. World Patent WO2011063806A1, 3 June 2011. [Google Scholar]
- Press Release, Asahi Kasei Europe Gmbh, Polyamide Foam Product. 2019. Available online: https://www.asahi-kasei.eu/en/News/Premiere%20for%20PA%20Foam%20%E2%80%93%20Asahi%20Kasei%20at%20Foam%20Expo%20Europe%202019_n261 (accessed on 19 October 2020).
- Press Release, BASF SE, BASF. Entwickelt UltramidPartikelschaum für Breites Anwendungsspektrum. 2019. Available online: www.basf.com/global/de/media/news-release/2019/10/p-19-360.html (accessed on 9 November 2020).
- Hahn, K.; Hofmann, M.; Ruckdäschel, H.; Sandler, J.K.W.; Scherzer, D. Particle Foam Based on a Polymer including Polystyrene, Styrene Copolymer, Polysulfone or Polyethersulfone, Comprises Inorganic Filler e.g., Talc Having Specified Particle Size and Wax or Oligomer Based Nucleating Agent e.g., Polyethylene Wax. Application DE102011110216A1, 23 February 2012. [Google Scholar]
- Köppl, T.; Raps, D.; Altstädt, V. E-PBT-Bead foaming of poly(butylene terephthalate) by underwater pelletizing. J. Cell. Plast. 2014, 50, 475–487. [Google Scholar] [CrossRef]
- Standau, T.; Hädelt, B.; Schreier, P.; Altstädt, V. Development of a Bead Foam from an Engineering Polymer with Addition of Chain Extender: Expanded Polybutylene Terephthalate. Ind. Eng. Chem. Res. 2018, 57, 17170–17176. [Google Scholar] [CrossRef]
- Wool, R.P.; Yuan, B.; McGarel, O.J. Welding of polymer interfaces. Polym. Eng. Sci. 1989, 29, 1340–1367. [Google Scholar] [CrossRef]
- Kim, H.J.; Lee, K.; Lee, H.H. Healing of fractured polymers by interdiffusion. Polymer 1996, 37, 4593–4597. [Google Scholar] [CrossRef]
- Kim, Y.H.; Wool, R.P. A Theory of Healing at a Polymer Polymer Interface. Macromolecules 1983, 16, 1115–1120. [Google Scholar] [CrossRef]
- Qiu, H.; Bousmina, M. Determination of mutual diffusion coefficients at nonsymmetric polymer/polymer interfaces from rheometry. Macromolecules 2000, 33, 6588–6594. [Google Scholar] [CrossRef]
- Yang, F.; Pitchumani, R. Healing of thermoplastic polymers at an interface under nonisothermal conditions. Macromolecules 2002, 35, 3213–3224. [Google Scholar] [CrossRef]
- Rossacci, J.; Shivkumar, S. Influence of EPS bead fusion on pattern degradation and casting formation in the lost foam process. J. Mater. Sci. 2003, 38, 2321–2330. [Google Scholar] [CrossRef]
- Rossacci, J.; Shivkumar, S. Bead fusion in polystyrene foams. J. Mater. Sci. 2003, 38, 201–206. [Google Scholar] [CrossRef]
- Klempner, D.; Frisch, K. Handbook of Polymeric Foams and Foam Technology; Hanser: München, Germany, 2004; ISBN 1569903360. [Google Scholar]
- Nakai, S.; Taki, K.; Tsujimura, I.; Ohshima, M. Numerical simulation of a polypropylene foam bead expansion process. Polym. Eng. Sci. 2008, 48, 107–115. [Google Scholar] [CrossRef]
- Illers, K.H. Heat of fusion and specific volume of poly(ethylene terephthalate) and poly(butylene terephthalate. Colloid Polym. Sci. 1980, 258, 117–124. [Google Scholar] [CrossRef]
- Khanna, Y.P.; Kuhn, W.P. Measurement of crystalline index in nylons by DSC: Complexities and recommendations. J. Polym. Sci. Part B Polym. Phys. 1997, 35, 2219–2231. [Google Scholar] [CrossRef]
- Jeziorny, A. Parameters characterizing the kinetics of the non-isothermal crystallization of poly (ethylene terephthalate) determined by d.s.c. Polymer 1978, 19, 1142–1144. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of Phase Change. I General Theory. J. Chem. Phys. 1939, 7, 1103–1112. [Google Scholar] [CrossRef]
- Avrami, M. Kinetics of Phase Change. II Transformation-Time Relations for Random Distribution of Nuclei. J. Chem. Phys. 1940, 8, 212–224. [Google Scholar] [CrossRef]
- Lorenzo, A.T.; Arnal, M.L.; Albuerne, J.; Müller, A.J. DSC isothermal polymer crystallization kinetics measurements and the use of the Avrami equation to fit the data: Guidelines to avoid common problems. Polym. Test. 2007, 26, 222–231. [Google Scholar] [CrossRef]
- Mihai, M.; Huneault, M.A.; Favis, B.D. Crystallinity development in cellular poly(lactic acid) in the presence of supercritical carbon dioxide. J. Appl. Polym. Sci. 2009, 113, 2920–2932. [Google Scholar] [CrossRef] [Green Version]
- van Meerveld, J.; Peters, G.W.M.; Hütter, M. Towards a rheological classification of flow induced crystallization experiments of polymer melts. Rheol. Acta 2004, 44, 119–134. [Google Scholar] [CrossRef] [Green Version]
- Villalobos, M.; Awojulu, A.; Greeley, T.; Turco, G.; Deeter, G. Oligomeric chain extenders for economic reprocessing and recycling of condensation plastics. Energy 2006, 31, 3227–3234. [Google Scholar] [CrossRef]
- Rathi, S.; Coughlin, E.; Hsu, S.; Golub, C.; Ling, G.; Tzivanis, M. Maintaining Structural Stability of Poly(lactic acid): Effects of Multifunctional Epoxy based Reactive Oligomers. Polymers (Basel) 2014, 6, 1232–1250. [Google Scholar] [CrossRef] [Green Version]
- Zeng, W.; Liu, J.; Zhou, J.; Dong, J.; Yan, S. A comparison study on the melt crystallization kinetics of long chain branched and linear isotactic polypropylenes. Chin. Sci. Bull. 2008, 53, 188–197. [Google Scholar] [CrossRef]
- Tabatabaei, S.H.; Carreau, P.J.; Ajji, A. Rheological and thermal properties of blends of a long-chain branched polypropylene and different linear polypropylenes. Chem. Eng. Sci. 2009, 64, 4719–4731. [Google Scholar] [CrossRef]
- McKee, M.G.; Unal, S.; Wilkes, G.L.; Long, T.E. Branched polyesters: Recent advances in synthesis and performance. Prog. Polym. Sci. 2005, 30, 507–539. [Google Scholar] [CrossRef]
- Dorgan, J.R.; Lehermeier, H.; Mang, M. Thermal and Rheological Properties of Commercial-Grade Poly (Lactic Acid)s. J. Polym. Environ. 2000, 8, 1–9. [Google Scholar] [CrossRef]
- Deshmukh, G.S.; Peshwe, D.R.; Pathak, S.U.; Ekhe, J.D. Nonisothermal crystallization kinetics and melting behavior of poly (butylene terephthalate) (PBT) composites based on different types of functional fillers. Thermochim. Acta 2014, 581, 41–53. [Google Scholar] [CrossRef]
- Lehmann, B.; Kocsis, K.J. Isothermal and non-isothermal crystallisation kinetics of pCBT and PBT: Polymers as studied by DSC. J. Therm. Anal. Calorim. 2009, 95, 221–227. [Google Scholar] [CrossRef]
- Huang, J.W. Poly (butylene terephthalate)/clay nanocomposite compatibilized with poly(ethylene- co -glycidyl methacrylate). I. Isothermal crystallization. J. Appl. Polym. Sci. 2008, 110, 2195–2204. [Google Scholar] [CrossRef]
- Wu, D.; Zhou, C.; Fan, X.; Mao, D.; Bian, Z. Morphology, Crystalline Structure and Isothermal Crystallization Kinetics of Polybutylene Terephthalate/Montmorillonite Nanocomposites. Polym. Polym. Compos. 2005, 13, 61–71. [Google Scholar] [CrossRef]
- Mulla, A.A.; Mathew, J.; Shanks, R. Isothermal crystallization studies of poly(butylene terephthalate) composites. J. Polym. Sci. Part B Polym. Phys. 2007, 45, 1344–1353. [Google Scholar] [CrossRef]
- Piorkowska, E.; Galeski, A. Overall Crystallization Kinetics. In Handbook of Polymer Crystallization; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2013; pp. 215–236. [Google Scholar] [CrossRef]
- Zou, P.; Tang, S.; Fu, Z.; Xiong, H. Isothermal and non-isothermal crystallization kinetics of modified rape straw flour/high-density polyethylene composites. Int. J. Therm. Sci. 2009, 48, 837–846. [Google Scholar] [CrossRef]
- Kissinger, H.E. Variation of peak temperature with heating rate in differential thermal analysis. J. Res. Natl. Bur. Stand. 1956, 57, 217. [Google Scholar] [CrossRef]
- Oburoğlu, N.; Ercan, N.; Durmus, A.; Kaşgöz, A. Effects of filler type on the nonisothermal crystallization kinetics of poly(butylene terephthalate) (PBT) composites. J. Appl. Polym. Sci. 2012, 123, 77–91. [Google Scholar] [CrossRef]
- Yadav, Y.S.; Jain, P.C.; Nanda, V.S. Use of differential scanning calorimetry to study polymer crystallization kinetics with longer half times. Thermochim. Acta 1983, 71, 313–321. [Google Scholar] [CrossRef]
- Wang, F.; Wang, H.; Zheng, K.; Chen, L.; Zhang, X.; Tian, X. Isothermal crystallization kinetics and mechanical properties of poly(butylene terephthalate)/attapulgite nanocomposites. Colloid Polym. Sci. 2014, 292, 953–963. [Google Scholar] [CrossRef]
- Yao, X.; Tian, X.; Zhang, X.; Zheng, K.; Zheng, J.; Wang, R.; Kang, S.; Cui, P. Preparation and characterization of poly(butylene terephthalate)/silica nanocomposites. Polym. Eng. Sci. 2009, 49, 799–807. [Google Scholar] [CrossRef]
- Kulshreshtha, B.; Ghosh, A.K.; Misra, A. Crystallization kinetics and morphological behavior of reactively processed PBT/epoxy blends. Polymer 2003, 44, 4723–4734. [Google Scholar] [CrossRef]
- Schulz, E.; Wunderlich, B. Macromolecular Physics, Volume 2 Crystal Nucleation, Growth, Annealing; Academic Press: New York, NY, USA, 1977; Volume 12, pp. K11–K12. [Google Scholar] [CrossRef]
- Cebe, P.; Hong, S.D. Crystallization behaviour of poly(ether-ether-ketone). Polymer 1986, 27, 1183–1192. [Google Scholar] [CrossRef]
- Xu, Y.; Ye, S.R.; Bian, J.; Qian, J.-W. Crystallization kinetics analysis of poly(trimethylene terephthalate) including the secondary crystallization process. J. Mater. Sci. 2004, 39, 5551–5555. [Google Scholar] [CrossRef]
- Zachmann, H.G. New insights into the structure and phase transitions of polymers. Nucl. Instrum. Methods Phys. Res. Sect. B Beam Interact. Mater. Atoms. 1995, 97, 209–215. [Google Scholar] [CrossRef]
- Wang, Z.G.; Hsiao, B.S.; Sauer, B.B.; Kampert, W.G. The nature of secondary crystallization in poly(ethylene terephthalate). Polymer 1999, 40, 4615–4627. [Google Scholar] [CrossRef]














| Neat E-PBT Outer Layer | Neat E-PBT Core | E-PBT + 1 wt. % CE Outer Layer | E-PBT + 1 wt. % CE Core | |
|---|---|---|---|---|
| Tm/°C | 224.6 | 224.1 | 222.9 | 222.1 |
| /% | 37.2 | 32.5 | 31.8 | 26.3 |
| Hm/J/g | 52.1 | 45.5 | 44.8 | 36.9 |
| Tonset − Toffset/°C | 209–240 | 212–238 | 209–233 | 212–232 |
| Neat E-PBT | τ1/2/min | Avrami Range (Tonset − Toffset) | |
|---|---|---|---|
| −2.5 K/min | 39.17 | 2.00 | 206–190 °C |
| −5 K/min | 38.85 | 1.30 | 203–185 °C |
| −10 K/min | 36.25 | 0.70 | 201–171 °C |
| −20 K/min | 34.21 | 0.45 | 199–158 °C |
| E-PBT + 1 wt. % CE | |||
| −2.5 K/min | 36.71 | 2.30 | 208–187 °C |
| −5 K/min | 36.31 | 1.60 | 205–182 °C |
| −10 K/min | 35.65 | 0.85 | 203–163 °C |
| −20 K/min | 32.70 | 0.55 | 201–155 °C |
| Neat E-PBT | n | kc (min−n) |
|---|---|---|
| −2.5 K/min | 3.23 | 0.34 |
| −5 K/min | 3.46 | 0.76 |
| −10 K/min | 3.44 | 1.08 |
| −20 K/min | 3.42 | 1.16 |
| E-PBT + 1 wt. % CE | ||
| −2.5 K/min | 4.28 | 0.19 |
| −5 K/min | 4.24 | 0.63 |
| −10 K/min | 4.10 | 0.99 |
| −20 K/min | 3.95 | 1.08 |
| Neat E-PBT | τ1/2/min | |
|---|---|---|
| 190 °C | 16.24 | 0.23 |
| 195 °C | 21.58 | 0.37 |
| 200 °C | 28.01 | 0.65 |
| 205 °C | 31.45 | 1.80 |
| E-PBT + 1 wt. % CE | ||
| 190 °C | 13.92 | 0.25 |
| 195 °C | 18.33 | 0.37 |
| 200 °C | 22.82 | 0.90 |
| 205 °C | 26.88 | 2.40 |
| Neat E-PBT | n | k (min−n) |
|---|---|---|
| 190 °C | 2.38 | 24.87 |
| 195 °C | 2.30 | 14.04 |
| 200 °C | 2.40 | 1.93 |
| 205 °C | 2.70 | 0.52 |
| E-PBT + 1 wt. % CE | ||
| 190 °C | 2.60 | 13.80 |
| 195 °C | 2.60 | 6.52 |
| 200 °C | 2.70 | 1.69 |
| 205 °C | 2.80 | 0.06 |
| Neat E-PBT | τ1/2/min | |
|---|---|---|
| 190 °C | 0.46 | 0.10 |
| 195 °C | 1.86 | 0.13 |
| 200 °C | 2.20 | 0.15 |
| 205 °C | 3.09 | 0.17 |
| E-PBT + 1 wt. % CE | ||
| 190 °C | 0.23 | 0.12 |
| 195 °C | 1.24 | 0.15 |
| 200 °C | 1.60 | 0.18 |
| 205 °C | 1.80 | 0.20 |
| Neat E-PBT | n | k/min-n |
|---|---|---|
| 190 °C | 1.45 | 17.46 |
| 195 °C | 1.47 | 14.88 |
| 200 °C | 1.47 | 12.06 |
| 205 °C | 1.46 | 9.58 |
| E-PBT + 1 wt. % CE | ||
| 190 °C | 1.42 | 14.73 |
| 195 °C | 1.37 | 10.07 |
| 200 °C | 1.42 | 8.25 |
| 205 °C | 1.42 | 6.68 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kuhnigk, J.; Raps, D.; Standau, T.; Luik, M.; Altstädt, V.; Ruckdäschel, H. Insights into the Bead Fusion Mechanism of Expanded Polybutylene Terephthalate (E-PBT). Polymers 2021, 13, 582. https://doi.org/10.3390/polym13040582
Kuhnigk J, Raps D, Standau T, Luik M, Altstädt V, Ruckdäschel H. Insights into the Bead Fusion Mechanism of Expanded Polybutylene Terephthalate (E-PBT). Polymers. 2021; 13(4):582. https://doi.org/10.3390/polym13040582
Chicago/Turabian StyleKuhnigk, Justus, Daniel Raps, Tobias Standau, Marius Luik, Volker Altstädt, and Holger Ruckdäschel. 2021. "Insights into the Bead Fusion Mechanism of Expanded Polybutylene Terephthalate (E-PBT)" Polymers 13, no. 4: 582. https://doi.org/10.3390/polym13040582
APA StyleKuhnigk, J., Raps, D., Standau, T., Luik, M., Altstädt, V., & Ruckdäschel, H. (2021). Insights into the Bead Fusion Mechanism of Expanded Polybutylene Terephthalate (E-PBT). Polymers, 13(4), 582. https://doi.org/10.3390/polym13040582