Rheological Basics for Modeling of Extrusion Process of Wood Polymer Composites
Abstract
:1. Introduction
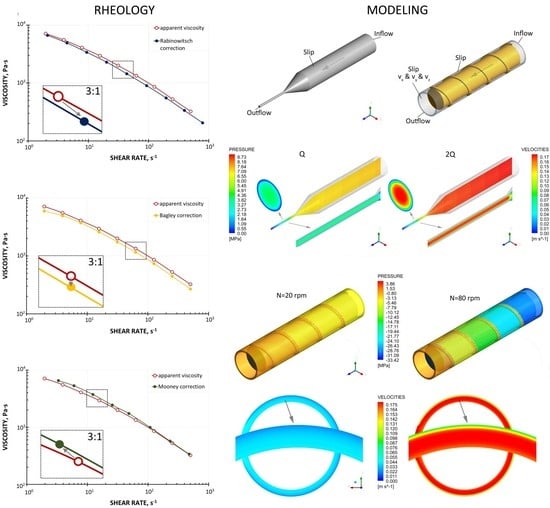
2. Material and Rheological Studies
3. FEM Flow Modeling
4. Extrusion Modeling
- Solid conveying section;
- delay section;
- melting section, the model is dependent on the filler content, a one-dimensional model for less than 50% filler is used, a two-dimensional model for over 50% filler is used (Figure 1);
- screw melt conveying section including slip effects using three-dimensional, non-Newtonian flow characteristics;
- die flow section with slip effects using three-dimensional, non-Newtonian flow characteristics.
5. Process Simulations
6. Experimental
7. Conclusions
- -
- Processing of the materials characterized by wall slip,
- -
- processing of filled/reinforced polymeric materials (by extrusion and injection molding),
- -
- food and cosmetics processing,
- -
- pharmaceutical industry [54],
- -
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Nova-Institut GmbH. Available online: http://news.bio-based.eu/new-market-and-trend-report-published (accessed on 21 November 2017).
- Grand View Research 2019, Wood Plastic Composite Market Size, Share & Trends Analysis Report by Type (PE, PP, PVC), Application, Region, Segment Forecasts, 2020–2027. Available online: https://www.grandviewresearch.com/industry-analysis/wood-plastic-composites-market (accessed on 1 February 2020).
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J.; Buziak, K. Experimental Study for Extrusion of Polypropylene/Wood Flour Composites. Int. Polym. Process. 2015, 30, 113–120. [Google Scholar] [CrossRef]
- Wilczyński, K.; Buziak, K.; Wilczyński, K.J.; Lewandowski, A.; Nastaj, A. Computer Modeling for Single-Screw Extrusion of Wood-Plastic Composites. Polymers 2018, 10, 295. [Google Scholar] [CrossRef] [Green Version]
- Xiao, K.; Tzoganakis, C. Rheological Properties and Their Influence on Extrusion Characteristics of HDPE-Wood Composite Resins. SPE ANTEC 2002, 39, 252–257. [Google Scholar]
- Xiao, K.; Tzoganakis, C. Extrusion Characteristic of HDPE-Wood Composites. SPE ANTEC 2003, 39, 197–201. [Google Scholar]
- Xiao, K.; Tzoganakis, C. Rheological Properties of HDPE-Wood Composites. SPE ANTEC 2003, 39, 975–979. [Google Scholar]
- Xiao, K.; Tzoganakis, C. Extrusiom of HDPE-Wood Blends. SPE ANTEC 2004, 40, 448–453. [Google Scholar]
- Li, T.Q.; Wolcott, M.P. Rheology of Wood Plastics Melt. Part 1. Capillary Rheometry of HDPE Filled with Maple. Polym. Eng. Sci. 2005, 45, 549–559. [Google Scholar] [CrossRef]
- Li, T.Q.; Wolcott, M.P. Rheology of Wood Plastics Melt, Part 2: Effects of Lubricating Systems in HDPE/Maple Composites. Polym. Eng. Sci. 2006, 46, 464–473. [Google Scholar] [CrossRef]
- Li, T.Q.; Wolcott, M.P. Rheology of Wood Plastics Melt, Part 3: NonLinear Nature of the Flow. Polym. Eng. Sci. 2006, 46, 114–121. [Google Scholar] [CrossRef]
- Błędzki, A.K.; Reihmane, S.; Gassan, J. Thermoplastics Reinforced with Wood Fillers: A Literature Review. Polym.-Plast. Technol. Eng. 1998, 37, 451–468. [Google Scholar] [CrossRef]
- Mohanty, A.K.; Misra, M.; Drzal, L.T. Natural Fibers, Biopolymers, and Biocomposites; Taylor & Francis: Boca Raton, FL, USA, 2005; ISBN 978-084-931-741-5. [Google Scholar]
- Klyosov, A.A. Wood-Plastic Composites; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2007. [Google Scholar] [CrossRef]
- Oksman Niska, K.; Sain, M. Wood-Polymer Composites; Woodhead Publishing: Cambridge, UK, 2008. [Google Scholar]
- Hristov, V.; Takács, E.; Vlachopoulos, J. Surface Tearing and Wall Slip Phenomena in Extrusion of Highly Filled HDPE/Wood Flour Composites. Polym. Eng. Sci. 2006, 46, 1204–1214. [Google Scholar] [CrossRef]
- Vlachopoulos, J.; Hristov, V. Rheology of Wood Polymer Composites. In Proceedings of the Regional PPS Meeting, Pretoria, South Africa, 9–13 October 2006. [Google Scholar]
- Santi, C.R.; Hage, E.; Vlachopoulos, J.; Correa, C.A. Rheology and Processing of HDPE/Wood Flour Composites. Int. Polym. Process. 2009, 24, 346–353. [Google Scholar] [CrossRef]
- Zolfaghari, A.; Behravesh, A.H.; Shakouri, E.; Soury, E. Flow Balancing in Die Design of Wood Flour/HDPE Composite Extrusion Profiles with Consideration of Rheological Effect. Polym. Eng. Sci. 2010, 50, 543–549. [Google Scholar] [CrossRef]
- Lewandowski, A.; Wilczyński, K. Global Modeling of Single Screw Extrusion with Slip Effects. Int. Polym. Process. 2019, 34, 81–90. [Google Scholar] [CrossRef]
- Lewandowski, A.; Wilczyński, K. Global Modeling for Single Screw Extrusion of Viscoplastics. Int. Polym. Process. 2020, 35, 26–36. [Google Scholar] [CrossRef]
- Tadmor, Z.; Klein, I. Engineering Principles of Plasticating Extrusion; Van Nostrand Reinhold Co.: New York, NY, USA, 1970. [Google Scholar]
- White, J.L.; Potente, H. Screw Extrusion; Hanser: Munich, Germany, 2003. [Google Scholar]
- Tadmor, Z.; Gogos, C. Principles of Polymer Processing; Wiley & Sons: New York, NY, USA, 2006. [Google Scholar]
- Rauwendaal, C. Polymer Extrusion; Hanser: Munich, Germany, 2013. [Google Scholar] [CrossRef]
- Agur, E.E.; Vlachopoulos, J. Numerical Simulation of a Single-Screw Plasticating Extruder. Polym. Eng. Sci. 1982, 22, 1084–1094. [Google Scholar] [CrossRef]
- Vincelette, A.R.; Guerrero, C.S.; Carreau, P.J.; Lafleur, P.G. A Model for Single-Screw Plasticating Extruders. Int. Polym. Process. 1989, 4, 232–241. [Google Scholar] [CrossRef]
- Potente, H.; Hanhart, W.; Schöppner, V. Potential Applications for Computer-Aided Extruder Design. Int. Polym. Process. 1993, 8, 335–344. [Google Scholar] [CrossRef]
- Wilczyński, K. Single Screw Extrusion Model for Plasticating Extruders. Polym.-Plast. Technol. Eng. 1999, 38, 581–608. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Nastaj, A.; Wilczyński, K. A Computer Model for Starve-Fed Single-Screw Extrusion of Polymer Blends. Adv. Polym. Technol. 2018, 37, 2142–2151. [Google Scholar] [CrossRef]
- Ilinca, F.; Hétu, J.-F. Three-Dimensional Finite Element Solution of the Flow in Single and Twin-Screw Extruders. Int. Polym. Process. 2010, 25, 275–286. [Google Scholar] [CrossRef] [Green Version]
- Altınkaynak, A.; Gupta, M.; Spalding, M.A.; Crabtree, S.L. Melting in a Single Screw Extruder: Experiments and 3D Finite Element Simulations. Int. Polym. Process. 2011, 26, 182–196. [Google Scholar] [CrossRef]
- Malik, M.; Kalyon, D.M.; Golba, J.C. Simulation of Co-Rotating Twin Screw Extrusion Process Subject to Pressure-Dependent Wall Slip at Barrel and Screw Surfaces: 3D FEM Analysis for Combinations of Forward- and Reverse-Conveying Screw Elements. Int. Polym. Process. 2014, 29, 51–62. [Google Scholar] [CrossRef]
- Teixeira, C.; Gaspar-Cunha, A.; Covas, J.A. Flow and Heat Transfer Along the Length of a Co-Rotating Twin Screw Extruder. Polym.-Plast. Technol. Eng. 2012, 51, 1567–1577. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J. Multipurpose Computer Model for Screw Processing of Plastics. Polym.-Plast. Technol. Eng. 2012, 51, 626–633. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J.; Buziak, K. Fundamentals of Global Modeling for Polymer Extrusion. Polymers 2019, 11, 2106. [Google Scholar] [CrossRef] [Green Version]
- Hyvärinen, M.; Jabeen, R.; Kärki, T. The Modelling of Extrusion Processes for Polymers—A Review. Polymers 2020, 12, 1306. [Google Scholar] [CrossRef]
- Potente, H.; Ridder, H.; Cunha, R.V. Global Concept for Describing and Investigation of Wall Slip Effects in the Extrusion Process. Macromol. Mater. Eng. 2002, 287, 836–842. [Google Scholar] [CrossRef]
- Potente, H.; Kurte-Jardin, M.; Klus, S.; Timmermann, K. Two Dimensional Description of Pressure-Throughput Behaviour of Newtonian Materials Considering Wall Slippage Effects. Int. Polym. Process. 2005, 20, 312–321. [Google Scholar] [CrossRef]
- Potente, H.; Timmermann, K.; Kurte-Jardin, M. Description of the Pressure/Throughput Behavior of a Single-Screw Plasticating Unit in Consideration of Wall Slippage Effects for Non-Newtonian Material and 1-D Flow. Int. Polym. Process. 2006, 21, 272–282. [Google Scholar] [CrossRef]
- Potente, H.; Bornemann, M.; Kurte-Jardin, M. Analytical Model for the Throughput and Drive Power Calculation in the Melting Section of Single Screw Plasticizing Units Considering Wall-Slippage. Int. Polym. Process. 2009, 24, 23–30. [Google Scholar] [CrossRef]
- Gooneie, A.; Schuschnigg, S.; Duretek, I.; Holzer, C. Numerical Simulations of the Flow of Wood Polypropylene Composites with Wall Slipping in a Profile Die: The Significance of Material Data. In AIP Conference Proceedings; AIP Publishing LLC: New York, NY, USA, 2015; p. 050014. [Google Scholar] [CrossRef]
- Duretek, I.; Schuschnigg, S.; Gooneie, A.; Langecker, G.R.; Holzer, C. Rheological Properties of Wood Polymer Composites and Their Role in Extrusion. J. Phys. Conf. Ser. 2015, 602, 012014. [Google Scholar] [CrossRef] [Green Version]
- Macosko, C.W. Rheology: Principles, Measurements and Applications; VCH Publishers: New York, NY, USA, 1994. [Google Scholar]
- Moigne, N.; Van den Oever, M.; Budtova, T. Dynamic and Capillary Shear Rheology of Natural Fiber-Reinforced Composites. Polym. Eng. Sci. 2013, 53, 2582–2593. [Google Scholar] [CrossRef]
- Polychronopoulos, N.D.; Charlton, Z.; Suwanda, D.; Vlachopoulos, J. Measurements and Comparison to Predictions of Viscosity of Heavily Filled HDPE with Natural Fibers. Adv. Polym. Technol. 2016, 37, 1161–1167. [Google Scholar] [CrossRef]
- Hatzikiriakos, S.G.; Dealy, J.M. Wall Slip of Molten High Density Polyethylenes. II. Capillary Rheometer Studies. J. Rheol. 1992, 36, 703–741. [Google Scholar] [CrossRef]
- Hatzikiriakos, S.G.; Dealy, J.M. Effects of Interfacial Conditions on Wall Slip and Sharkskin Melt Fracture of HDPE. Int. Polym. Process. 1993, 8, 36–43. [Google Scholar] [CrossRef]
- Hatzikiriakos, S.G. The Onset of Wall Slip and Sharkskin Melt Fracture in Capillary Flow. Polym. Eng. Sci. 1994, 34, 1441–1449. [Google Scholar] [CrossRef]
- Hatzikiriakos, S.G.; Mitsoulis, E. Slip Effects in Tapered Dies. Polym. Eng. Sci. 2009, 49, 1960–1969. [Google Scholar] [CrossRef]
- ANSYS Polyflow v.17. 2017. Available online: https://cfd.hu/doc/ansys_capabilities_170.pdf (accessed on 1 November 2020).
- Wilczyński, K.J.; Nastaj, A.; Lewandowski, A.; Wilczyński, K. A Composite Model for Starve Fed Single Screw Extrusion of Thermoplastics. Polym. Eng. Sci. 2014, 54, 2362–2374. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Buziak, K. Study on the Flow of Wood Plastic Composites in the Starve Fed Single Screw Extrusion. Polimery 2017, 62, 680–685. [Google Scholar] [CrossRef]
- Dhaval, M.; Sharma, S.; Dudhat, K.; Chavda, J. Twin-Screw Extruder in Pharmaceutical Industry: History, Working Principle, Applications, and Marketed Products: An In-depth Review. J. Pharm. Innov. 2020. [Google Scholar] [CrossRef]
- Rohani Rad, E.; Vahabi, H.; Formela, K.; Saeb, M.R.; Thomas, S. Injectable Poloxamer/Graphene Oxide Hydrogels with Well-Controlled Mechanical and Rheological Properties. Polym. Adv. Technol. 2019, 30, 2250–2260. [Google Scholar] [CrossRef]
- Schwab, A.; Levato, R.; D’Este, M.; Piluso, S.; Eglin, D.; Malda, J. Printability and Shape Fidelity of Bioinks in 3D Bioprinting. Chem. Rev. 2020, 120, 11028–11055. [Google Scholar] [CrossRef] [PubMed]
- La Galla, A.; Fiorio, R.; Erkoç, M.; Cardon, L.; D’hooge, D.R. Theoretical Evaluation of the Melting Efficiency for the Single-Screw Micro-Extrusion Process: The Case of 3D Printing of ABS. Processes 2020, 8, 1522. [Google Scholar] [CrossRef]

















| Screw Speed, rpm | Throughput (Predicted), kg/h | |
| No Slip | Slip | |
| 20 | 07.94 | 08.41 |
| 50 | 16.05 | 18.26 |
| 80 | 27.87 | 31.69 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wilczyński, K.; Buziak, K.; Lewandowski, A.; Nastaj, A.; Wilczyński, K.J. Rheological Basics for Modeling of Extrusion Process of Wood Polymer Composites. Polymers 2021, 13, 622. https://doi.org/10.3390/polym13040622
Wilczyński K, Buziak K, Lewandowski A, Nastaj A, Wilczyński KJ. Rheological Basics for Modeling of Extrusion Process of Wood Polymer Composites. Polymers. 2021; 13(4):622. https://doi.org/10.3390/polym13040622
Chicago/Turabian StyleWilczyński, Krzysztof, Kamila Buziak, Adrian Lewandowski, Andrzej Nastaj, and Krzysztof J. Wilczyński. 2021. "Rheological Basics for Modeling of Extrusion Process of Wood Polymer Composites" Polymers 13, no. 4: 622. https://doi.org/10.3390/polym13040622
APA StyleWilczyński, K., Buziak, K., Lewandowski, A., Nastaj, A., & Wilczyński, K. J. (2021). Rheological Basics for Modeling of Extrusion Process of Wood Polymer Composites. Polymers, 13(4), 622. https://doi.org/10.3390/polym13040622