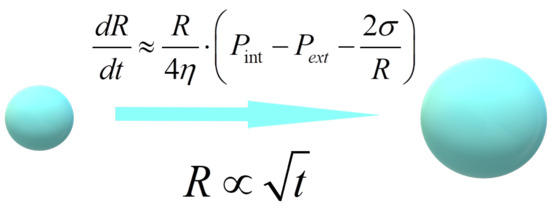Depressurization-Induced Nucleation in the “Polylactide-Carbon Dioxide” System: Self-Similarity of the Bubble Embryos Expansion
Abstract
:1. Introduction
- -
- Saturation of a raw polymer with a plasticizing/foaming agent by means of required exposure of a processed amount of polymer in an agent atmosphere at a given pressure and temperature;
- -
- Appearance of microscopic CO2-filled bubble embryos, randomly distributed in the volume of the plasticized polymer, and evolution of an ensemble of individual bubbles in the polymer volume up to the time of their closure into a foam-like structure during the pressure release;
- -
- Intensive expansion of the polymer foam with a subsequent stabilization of its structure at low pressures.
2. Materials and Methods
2.1. Materials
2.2. Methods
3. Modeling of Individual Bubble Expansion in the Depressurized System “Polylactide-Carbon Dioxide”
3.1. The Applied Kinetic Model
- -
- The concentration profile around a slowly expanding bubble embryo can be considered as a self-similar solution of a non-stationary diffusion equation, and the current cutoff radius is related to the current bubble radius as ;
- -
- The monotonically decaying term is considered as an expansion in the series of the powers of density , with only the first (linear) term taken into account; consequently, this term is assumed proportional to with a small proportionality coefficient: .
3.2. Self-Similarity of Bubble Expansion
3.3. A Transient Mode of the Bubble Embryo Expansion
4. Discussion of the Results
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lanza, R.; Langer, R.; Vacanti, J. Principles of Tissue Engineering, 4th ed.; Academic Press: New York, NY, USA, 2013; pp. 83–123. [Google Scholar]
- Zhang, X. Science and Principles of Biodegradable and Bioresorbable Medical Polymers. Materials and properties, 1st ed.; Woodhead Publishing: London, UK, 2017; pp. 1–476. [Google Scholar]
- Netti, P. (Ed.) Biomedical Foams for Tissue Engineering Applications, 1st ed.; Woodhead Publishing: London, UK, 2014; pp. 1–446. [Google Scholar]
- Salerno, A.; Oliviero, M.; Di Maio, E.; Iannace, S.; Netti, P. Design of porous polymeric scaffolds by gas foaming of heterogeneous blends. J. Mater. Sci. Mater. Med. 2009, 20, 2043–2051. [Google Scholar] [CrossRef]
- Cooper, A.I. Porous materials and supercritical fluids. Adv. Mater. 2003, 15, 1049–1059. [Google Scholar] [CrossRef]
- Reverchon, E.; Cardea, S. Production of controlled polymeric foams by supercritical CO2. J. Supercrit. Fluids 2007, 40, 144–152. [Google Scholar] [CrossRef]
- Tai, H.; Mather, M.L.; Howard, D.; Wang, W.; White, L.J.; Crowe, J.A.; Morgan, S.P.; Chandra, A.; Williams, D.J.; Howdle, S.; et al. Control of pore size and structure of tissue engineering scaffolds produced by supercritical fluid processing. Eur. Cells Mater. 2007, 14, 64–77. [Google Scholar] [CrossRef]
- Bogorodskii, S.E.; Zarkhina, T.S.; Kuzhetsov, E.V.; Minaeva, S.A.; Popov, V.K.; Solov’eva, A.B.; Timashev, P.S. Morphological changes of the polylactic acid microstructure under the action of supercritical carbon dioxide. Russ. J. Phys. Chem. B 2014, 8, 924–931. [Google Scholar] [CrossRef]
- Tai, H.; Popov, V.; Shakesheff, K.; Howdle, S. Putting the fizz into chemistry: Applications of supercritical carbon dioxide in tissue engineering, drug delivery and synthesis of novel block copolymers. Biochem. Soc. Trans. 2007, 35, 516–521. [Google Scholar] [CrossRef] [PubMed]
- Ruiz, J.A.R.; Vincent, M.; Agassant, J.-F.; Sadik, T.; Pillon, C.; Carrot, C. Polymer foaming with chemical blowing agents: Experiment and modeling. Polym. Eng. Sci. 2015, 55, 2018–2029. [Google Scholar] [CrossRef]
- Shine, A.D. Polymers and Supercritical Fluids. In Physical Properties of Polymers Handbook; Mark, J.E., Ed.; Springer: New York, NY, USA, 2007. [Google Scholar]
- Tsivintzelis, I.; Sanxaridou, G.; Pavlidou, E.; Panayiotou, C. Foaming of polymers with supercritical fluids: A thermodynamic investigation. J. Supercrit. Fluids 2016, 110, 240–250. [Google Scholar] [CrossRef]
- Karimi, M.; Heuchel, M.; Weigel, T.; Schossig, M.; Hoffmann, D.; Lendlein, A. Formation and size distribution of pores in poly(ε-caprolactone) foams prepared by pressure quenching using supercritical CO2. J. Supercrit. Fluids 2012, 61, 175–190. [Google Scholar] [CrossRef]
- White, L.J.; Hutter, V.; Tai, H.; Howdle, S.M.; Shakesheff, K.M. The effect of processing variables on morphological and mechanical properties of supercritical CO2 foamed scaffolds for tissue engineering. Acta Biomater. 2012, 8, 61–71. [Google Scholar] [CrossRef] [Green Version]
- Mathieu, L.M.; Montjovent, M.-O.; Bourban, P.-E.; Pioletti, D.P.; Månson, J.-A.E. Bioresorbable composites prepared by supercritical fluid foaming. J. Biomed. Mater. Res. A 2005, 75, 89–97. [Google Scholar] [CrossRef]
- Zhao, B.; Hamidinejad, M.; Zhao, C.; Li, R.; Wang, S.; Kazemi, Y.; Park, C.B. A versatile foaming platform to fabricate polymer/carbon composites with high dielectric permittivity and ultra-low dielectric loss. J. Mater. Chem. A 2019, 7, 133–140. [Google Scholar] [CrossRef]
- Zhao, B.; Zhao, C.; Wang, C.; Park, C.B. Poly (vinylidene fluoride) foams: A promising low-k dielectric and heat-insulating material. J. Mater. Chem. C 2018, 6, 3065–3073. [Google Scholar] [CrossRef]
- Wu, Y.; Wang, Z.; Liu, X.; Shen, X.; Zheng, Q.; Xue, Q.; Kim, J.-K. Ultralight graphene foam/conductive polymer composites for exceptional electromagnetic interference shielding. ACS Appl. Mater. Interfaces 2017, 9, 9059–9069. [Google Scholar] [CrossRef] [PubMed]
- Hou, J.; Zhao, G.; Wang, G.; Dong, G.; Xu, J. A novel gas-assisted microcellular injection molding method for preparing lightweight foams with superior surface appearance and enhanced mechanical performance. Mater. Des. 2017, 127, 115–125. [Google Scholar] [CrossRef]
- Zhao, J.; Zhao, Q.; Wang, C.; Guo, B.; Park, C.B.; Wang, G. High thermal insulation and compressive strength polypropylene foams fabricated by high-pressure foam injection molding and mold opening of nano-fibrillar composites. Mater. Des. 2017, 131, 1–11. [Google Scholar] [CrossRef]
- Cheng, J.J.; Qu, W.J.; Sun, S.H. Mechanical properties improvement and fire hazard reduction of expandable graphite microencapsulated in rigid polyurethane foams. Polym. Compos. 2019, 40, E1006–E1014. [Google Scholar] [CrossRef]
- Zhou, Y.-G.; Chen, T.-Y. Combining foam injection molding with batch foaming to improve cell density and control cellular orientation via multiple gas dissolution and desorption processes. Polym. Adv. Technol. 2020, 31, 2136–2151. [Google Scholar] [CrossRef]
- Zimnyakov, D.A.; Bagratshvili, V.N.; Yuvchenko, S.A.; Slavnetskov, I.O.; Kalacheva, A.V.; Ushakova, O.V.; Markova, N.S. Quasi-adiabatic expansion of the polylactide foam: Features of the porous matrices formation in the region of transition between sub–and supercritical states of plasticizing carbon dioxide. Russ. J. Phys. Chem. B 2019, 13, 1254–1265. [Google Scholar] [CrossRef]
- Zimnyakov, D.A.; Epifanov, E.O.; Kalacheva, A.V.; Minaev, N.V.; Minaeva, S.A.; Popov, V.K.; Samorodina, T.V.; Slavnetskov, I.O.; Ushakova, E.V.; Ushakova, O.V. Peculiarities of quasi-isothermal foaming of the SCF-plasticized polylactide: The effect of transition from foam expansion to its collapse. Russ. J. Phys. Chem. B 2020, 14, 1236–1243. [Google Scholar] [CrossRef]
- Zimnyakov, D.A.; Popov, V.K.; Minaev, N.V.; Epifanov, E.O.; Parenago, O.O.; Zdrajevsky, R.A.; Vereshagin, D.A.; Ushakova, O.V. Competition of phase separation processes during quasi-isothermal foaming of polylactide in carbon dioxide environment. Russ. J. Phys. Chem. B 2020, 14, 1268–1276. [Google Scholar] [CrossRef]
- Zimnyakov, D.; Zdrajevsky, R.; Minaev, N.; Epifanov, E.; Popov, V.; Ushakova, O. Extreme foaming modes for SCF-plasticized polylactides: Quasi-adiabatic and quasi-isothermal foam expansion. Polymers 2020, 12, 1055. [Google Scholar] [CrossRef]
- Gualandi, G.; White, L.J.; Chen, L.; Gross, R.A.; Shakesheff, K.M.; Howdle, S.M.; Scandola, M. Scaffold for tissue engineering fabricated by non-isothermal supercritical carbon dioxide foaming of a highly crystalline polyester. Acta Biomater. 2010, 6, 130–136. [Google Scholar] [CrossRef] [PubMed]
- Scriven, L.E. On the dynamics of phase growth. Chem. Eng. Sci. 1959, 10, 1–13. [Google Scholar] [CrossRef]
- Plesset, M.S.; Sadhal, S.S. On the stability of gas bubbles in liquid-gas solutions. Appl. Sci. Res. 1982, 38, 133–141. [Google Scholar] [CrossRef] [Green Version]
- Prosperetti, A.; Plesset, M.S. Vapour-bubble growth in a superheated fluid. J. Fluid Mech. 1978, 85, 349–368. [Google Scholar] [CrossRef] [Green Version]
- Tikuisis, P.; Ward, S.A.; Venter, R.D. Bubble evolution in a stirred volume of liquid closed to mass transport. J. Appl. Phys. 1983, 54, 1–9. [Google Scholar] [CrossRef]
- Ward, C.A.; Tikuisis, P.; Venter, R.D. Stability of bubbles in a closed volume of liquidgas solutions. J. Appl. Phys. 1982, 53, 6076–6084. [Google Scholar] [CrossRef]
- Mohammadein, S.A.; Mohamed, K.G. Concentration distribution around a growing gas bubble in tissue. Math. Biosci. 2010, 225, 11–17. [Google Scholar] [CrossRef]
- Han, C.D.; Yoo, H.J. Studies on structural foam processing. 4. Bubble growth during mold filling. Polym. Eng. Sci. 1981, 21, 518–533. [Google Scholar] [CrossRef]
- Payvar, P. Mass-transfer controlled bubble growth during rapid decompression of a liquid. Int. J. Heat Mass Transf. 1987, 30, 699–706. [Google Scholar] [CrossRef]
- Shafi, M.A.; Lee, J.G.; Flumerfelt, R.W. Prediction of cellular structure in free expansion polymer foam processing. Polym. Eng. Sci. 1996, 36, 1950–1959. [Google Scholar] [CrossRef]
- Dörr, D.; Standau, T.; Castellón, S.M.; Bonten, C.; Altstädt, V. Rheology in the presence of carbon dioxide (CO2) to study the melt behavior of chemically modified polylactide (PLA). Polymers 2020, 12, 1108. [Google Scholar] [CrossRef] [PubMed]
- Tai, H.; Upton, C.E.; White, L.J.; Pini, R.; Storti, G.; Mazzotti, M.; Shakesheff, K.M.; Howdle, S.M. Studies on the interactions of CO2 with biodegradable poly (DL-lactic acid) and poly (lactic acid-co-glycolic acid) copolymers using high pressure ATR-IR and high pressure rheology. Polymers 2010, 51, 1425–1431. [Google Scholar] [CrossRef]
- Mahmood, S.H.; Ameli, A.; Hossieny, N.; Park, C.B. The interfacial tension of molten polylactide in supercritical carbon dioxide. J. Chem. Thermodyn. 2014, 75, 69–76. [Google Scholar] [CrossRef]
- NIST Chemistry Web Book. Available online: https://webbook.nist.gov/chemistry/fluid/ (accessed on 12 January 2021).
- Taki, K. Experimental and numerical studies on the effects of pressure release rate on number density of bubbles and bubble growth in a polymeric foaming process. Chem. Eng. Sci. 2008, 63, 3643–3653. [Google Scholar] [CrossRef]
- De Yoreo, J.J.; Vekilov, P.G. Principles of crystal nucleation and growth. Rev. Mineral. Geochem. 2003, 54, 57–93. [Google Scholar] [CrossRef] [Green Version]
- Virnau, P.; Müller, M.; MacDowell, L.G.; Binder, K. Phase separation kinetics in compressible polymer solutions: Computer simulation of the early stages. N. J. Phys. 2004, 6, 7. [Google Scholar] [CrossRef]
- Binder, K.; Müller, M.; Virnau, P.; MacDowell, L.G. Polymer + solvent systems: Phase diagrams, interface free energies, and nucleation. Adv. Polym. Sci. 2005, 173, 1–110. [Google Scholar] [CrossRef]












| Number of the Dataset | , K | |
|---|---|---|
| 1 | 8.0 | 338 |
| 2 | 8.0 | 323 |
| 3 | 8.0 | 338 |
| 4 | 14.5 | 338 |
| 5 | 11.5 | 323 |
| 6 | 11.5 | 310 |
| Number of the Dataset | , K | |
|---|---|---|
| 1 | 11.5 | 310 |
| 2 | 7.0 | 323 |
| 3 | 11.5 | 323 |
| 4 | 14.5 | 333 |
| 5 | 7.0 | 310 |
| 6 | 14.5 | 338 |
| 7 | 14.5 | 323 |
| 8 | 8.0 | 323 |
| 9 | 8.0 | 338 |
| Number of the Dataset | ||
|---|---|---|
| 1 | 10.1 ± 2.5 | (2.9 ± 0.6) × 10−3 |
| 2 | 13.5 ± 3.2 | (2.8 ± 0.6) × 10−3 |
| 3 | 13.8 ± 3.3 | (2.9 ± 0.6) × 10−3 |
| 4 | 4.5 ± 1.0 | (1.8 ± 0.4) × 10−3 |
| 5 | 6.0 ± 1.5 | (2.0 ± 0.6) × 10−3 |
| 6 | 8.0 ± 1.9 | (2.2 ± 0.8) × 10−3 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zimnyakov, D.; Alonova, M.; Ushakova, E. Depressurization-Induced Nucleation in the “Polylactide-Carbon Dioxide” System: Self-Similarity of the Bubble Embryos Expansion. Polymers 2021, 13, 1115. https://doi.org/10.3390/polym13071115
Zimnyakov D, Alonova M, Ushakova E. Depressurization-Induced Nucleation in the “Polylactide-Carbon Dioxide” System: Self-Similarity of the Bubble Embryos Expansion. Polymers. 2021; 13(7):1115. https://doi.org/10.3390/polym13071115
Chicago/Turabian StyleZimnyakov, Dmitry, Marina Alonova, and Ekaterina Ushakova. 2021. "Depressurization-Induced Nucleation in the “Polylactide-Carbon Dioxide” System: Self-Similarity of the Bubble Embryos Expansion" Polymers 13, no. 7: 1115. https://doi.org/10.3390/polym13071115
APA StyleZimnyakov, D., Alonova, M., & Ushakova, E. (2021). Depressurization-Induced Nucleation in the “Polylactide-Carbon Dioxide” System: Self-Similarity of the Bubble Embryos Expansion. Polymers, 13(7), 1115. https://doi.org/10.3390/polym13071115