Influence of Carbon Black and Silica Fillers with Different Concentrations on Dielectric Relaxation in Nitrile Butadiene Rubber Investigated by Impedance Spectroscopy
Abstract
:1. Introduction
2. Materials and Methods
2.1. Sample Composition
2.2. Impedance Spectroscopy
2.3. Transmission Electron Microscopy and Differential Scanning Calorimeter
3. Relaxation Process and Model Function
3.1. α Relaxation Process
3.2. α′ Relaxation Process
3.3. Conductivity and Model Function
4. Results and Discussion
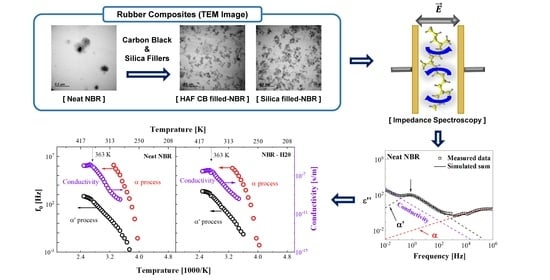
4.1. TEM
4.2. Impedance Spectroscopy at Room Temperature
4.3. Temperature Dependence of the Dielectric Relaxation
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Khawaja, M.; Sutton, A.P.; Mostofi, A.A. Molecular Simulation of Gas Solubility in Nitrile Butadiene Rubber. J. Phys. Chem. B 2017, 121, 287–297. [Google Scholar] [CrossRef] [Green Version]
- Fujiwara, H. Analysis of acrylonitrile butadiene rubber (NBR) expanded with penetrated hydrogen due to high pressure hydrogen exposure. Int. Polym. Sci. Technol. 2017, 44, 41–48. [Google Scholar] [CrossRef] [Green Version]
- Barth, R.R.; Simmons, K.L.; Marchi, C.S. Polymers for Hydrogen Infrastructure and Vehicle Fuel Systems: Applications, Properties, and Gap Analysis; Office of Scientific and Technical Information: Oak Ridge, TN, USA, 2013.
- Polymer Properties Database, O-Ring Seals. 2015. Available online: https://polymerdatabase.com/Elastomers/O-Ring_Elastomers.html (accessed on 20 November 2020).
- Nanda, M.; Chaudhary, R.; Tripathy, D. Dielectric relaxation of conductive carbon black reinforced chlorosulfonated polyethylene vulcanizates. Polym. Compos. 2020, 31, 152–162. [Google Scholar] [CrossRef]
- Das, N.; Chaki, T.; Khastgir, D.; Chakraborty, A. Electrical and mechanical properties of conductive carbon black filled EVA, EPDM and their blends. Kautsch. Gummi Kunstst. 2002, 55, 300–306. [Google Scholar]
- Karasek, L.; Sumita, M. Characterization of dispersion state of filler and polymer-filler interactions in rubber-carbon black composites. J. Mater. Sci. 1996, 31, 281–289. [Google Scholar] [CrossRef]
- Liu, J.S.; Wu, S.P.; Chen, M.Z.; Mi, Y.X. The Effect of Filler on the Properties of Silicone Rubber. Mater. Sci. Forum 2009, 620–622, 311–314. [Google Scholar] [CrossRef]
- Ulfah, I.M.; Fidyaningsih, R.; Rahayu, S.; Fitriani, D.A.; Saputra, D.A.; Winarto, D.A.; Wisojodharmo, L.A. Influence of Carbon Black and Silica Filler on the Rheological and Mechanical Properties of Natural Rubber Compound. Procedia Chem. 2015, 16, 258–264. [Google Scholar] [CrossRef] [Green Version]
- Stöckelhuber, K.W.; Svistkov, A.S.; Pelevin, A.G.; Heinrich, G. Impact of filler surface modiefication on large scale mechanism of Styelne Butadiene/Silica rubber composites. Macromolecules 2011, 44, 4366–4381. [Google Scholar] [CrossRef]
- Meier, J.G.; Mani, J.W.; Klüppel, M. Analysis of carbon black networking in elastomers by dielectric spectroscopy. Phys. Rev. B 2007, 75, 054202. [Google Scholar] [CrossRef]
- Rattanasom, N.; Saowapark, T.; Deeprasertkul, C. Reinforcement of natural rubber with silica/carbon black hybrid filler. Polym. Test. 2007, 26, 369–377. [Google Scholar] [CrossRef]
- Hashim, A.S.; Azahari, B.; Ikeda, Y.; Kohjiya, S. The Effect of Bis(3-Triethoxysilylpropyl) Tetrasulfide on Silica Reinforcement of Styrene-Butadiene Rubber. Rubber Chem. Technol. 1998, 71, 289–299. [Google Scholar] [CrossRef]
- Brinke, J.; Debnath, S.; Reuvekamp, L.; Noordermeer, J. Mechanistic aspects of the role of coupling agents in silica–rubber composites. Compos. Sci. Technol. 2003, 63, 1165–1174. [Google Scholar] [CrossRef]
- Suzuki, N.; Ito, M.; Ono, S. Effects of rubber/filler interactions on the structural development and mechanical properties of NBR/silica composites. J. Appl. Polym. Sci. 2005, 95, 74–81. [Google Scholar] [CrossRef]
- Lopez, J.F.; Perez, L.D.; Lopez, B.L. Effect of silica modification on the chemical interactions in NBR-based composites. J. Appl. Polym. Sci. 2011, 122, 2130–2138. [Google Scholar] [CrossRef]
- Wang, W.G.; Li, X.Y. Impedance and dielectric relaxation spectroscopy studies on the calcium modified Na0.5Bi0.44Ca0.06TiO2.97 ceramics. AIP Adv. 2017, 7, 125318. [Google Scholar] [CrossRef] [Green Version]
- Runt, J.P.; Fitzgerald, J.J. Dielectric Spectroscopy of Polymeric Materials Fundamentals and Applications, American Chemical Society: Washington, DC. J. Am. Chem. Soc. 1997, 119, 1202. [Google Scholar]
- Kremer, F.; Schonhalds, A. Broadband Dielectric Spectroscopy; Springer: Berlin, Germany, 2003. [Google Scholar]
- Dastan, D.; Banpurkar, A. Solution processable sol–gel derived titania gate dielectric for organic field effect transistors. J. Mater. Sci. Mater. Electron. 2017, 28, 3851–3859. [Google Scholar] [CrossRef]
- Dastan, D.; Gosavi, S.W.; Chaure, N.B. Studies on electrical properties of hybrid polymeric gate dielectrics for field effect transistors. Macromol. Symp. 2015, 347, 81–86. [Google Scholar] [CrossRef]
- Sun, C.; Zhang, P.; Wrana, C.; Schuster, R.; Zhao, S. Combined dielectric and mechanical investigation of filler network percolation behavior, filler-filler contact, and filler-polymer interaction on carbon black-filled hydrogenated acrylonitrile-butadiene rubber. Rubber Chem. Technol. 2014, 87, 647–663. [Google Scholar] [CrossRef]
- Xu, H.; Song, Y.; Jia, E.; Zheng, Q. Dynamics heterogeneity in silica-filled nitrile butadiene rubber. J. Appl. Polym. Sci. 2018, 135, 63–67. [Google Scholar] [CrossRef]
- Jung, J.K.; Moon, Y.I.; Kim, G.H.; Tak, N.H. Characterization of dielectric relaxation process by impedance spectroscopy for polymers: Nitrile butadiene rubber and ethylene propylene diene monomer. J. Spectrosc. 2020, 2020, 8815492. [Google Scholar] [CrossRef]
- Moon, Y.I.; Jung, J.K.; Kim, G.H.; Chung, K.S. Observation of the relaxation process in fluoroelastomers by dielectric relaxation spectroscopy. Phys. B Condens. Matter 2021, 608, 412870. [Google Scholar] [CrossRef]
- Stockmayer, W.H. Dielectric dispersion in solution of flexible polymers. Pure Appl. Chem. 1967, 15, 539. [Google Scholar] [CrossRef]
- Block, H. The nature and pllication of electrical phenomena in polymers. Adv. Polym. Sci. 1979, 33, 94. [Google Scholar]
- Van Krevelen, D.W. Properties of Polymers, 4th ed.; Elsevier: Amsterdam, The Netherlands, 2009. [Google Scholar]
- Kakani, S.L. Electronics Theory and Applications; New Age International Publisher: Delhi, India, 2011; p. 7. [Google Scholar]
- Dhahri, A.; Dhahri, E.; Hlil, E.K. Electrical conductivity and dielectric behaviour of nanocrystalline La0.6Gd0.1Sr0.3Mn0.75Si0.25O3. RSC Adv. 2018, 8, 9103–9111. [Google Scholar] [CrossRef] [Green Version]
- Vassilikou-Dove, A.; Kalogeras, M. Dielectric analysis (DEA). In Thermal Analysis of Polymers, Fundamentals and Applications; Menczel, J.D., Prime, R.B., Eds.; Wiley: New Jersey, NJ, USA, 2009; pp. 497–614. [Google Scholar]
- Raju, G.G. Dielectric in Electric Fields; Marcel Dekker Inc.: New York, NY, USA, 2003. [Google Scholar]
- Fu, S.Y.; Lauke, B.; Mai, Y.W. Science and Engineering of Short Fiber Reinforced Polymer Composites; Woodhead Publishing: Cambridge, MA, USA, 2009. [Google Scholar]
- Vieweg, S.; Unger, R.; Heinrich, G.; Donth, E. Comparison of dynamic shear properties of styrene–butadiene vulcanizates filled with carbon black or polymeric fillers. J. Appl. Polym. Sci. 1999, 73, 495–503. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, W.; Zhang, J.; Ni, Y. Dielectric relaxation processes in PVDF composite. Polym. Test. 2020, 91, 10680. [Google Scholar] [CrossRef]
- Robertson, C.G.; Lin, C.J.; Rackaitis, M.; Roland, C.M. Influence of Particle Size and Polymer−Filler Coupling on Viscoelastic Glass Transition of Particle-Reinforced Polymers. Macromolecules 2008, 41, 2727–2731. [Google Scholar] [CrossRef] [Green Version]
- Robertson, C.; Roland, C.M. Glass Transition and Interfacial Segmental Dynamics in Polymer-Particle Composites. Rubber Chem. Technol. 2008, 81, 506–522. [Google Scholar] [CrossRef]
- Gurovich, D.; Macosko, C.W.; Tirrell, M. The Influence of Filler-Filler and Filler-Polymer Interactions on the Physical Properties of Silica-Filled Liquid Polyisoprene. Rubber Chem. Technol. 2004, 77, 1–12. [Google Scholar] [CrossRef]
- Vikulova, M.; Tsyganov, A.; Bainyashev, A.; Artyukhov, D.; Gorokhovsky, A.; Muratov, D.; Gorshkov, N. Dielectric properties of PMMA/KCTO (H) composites for electronics components. J. Appl. Polym. Sci. 2021, 138, 51168. [Google Scholar] [CrossRef]
- Moon, Y.I.; Jung, J.K.; Chung, K.S. Dielectric Relaxation Spectroscopy in Synthetic Rubber Polymers: Nitrile Butadiene Rubber and Ethylene Propylene Diene Monomer. Adv. Mater. Sci. Eng. 2020, 2020, 8406059. [Google Scholar] [CrossRef]
- Pissis, P.; Fragiadakis, D.; Kanapitsas, A. Broadband Dielectric Spectroscopy for Studying Morphology and Interfacial Effects in Polymer Nanocomposites (n.d.). In Proceedings of the 11th European Conference on Conposite materials-ECCM11, Rhodes, Greece, 31 May–3 June 2004. [Google Scholar]
- AlZamil, M.A.; Alfaramawi, K.; Abboudy, S.; Abulnasr, L. Temperature Coefficients of Electrical Conductivity and Conduction Mechanisms in Butyl Rubber-Carbon Black Composites. J. Electron. Mater. 2017, 47, 1665–1672. [Google Scholar] [CrossRef]
- Nguyen, D.H.; Sylvestre, A.; Gonon, P.; Rowe, S. Dielectric properties analysis of silicone rubber. In Proceedings of the 2004 IEEE International Conference on Solid Dielectrics, Toulouse, France, 5–9 July 2004; pp. 103–106. [Google Scholar]
- Dong, H.; Jia, Z.; Chen, Y.; Luo, Y.; Zhong, B.; Jia, D. One-pot method to reduce and functionalize graphene oxide via vulcanization accelerator for robust elastomer composites with high thermal conductivity. Compos. Sci. Technol. 2018, 164, 267–273. [Google Scholar] [CrossRef]
- Fröhlich, J.; Niedermeier, W.; Luginsland, H.D. The effect of filler-filler and filler-elastomer interaction on rubber reinforcement. Compos. Part A Appl. Sci. Manuf. 2005, 36, 449–460. [Google Scholar] [CrossRef]
- Litvinov, V.M.; Orza, R.A.; Klüppel, M.; van Duin, M.; Magusin, P.C.M.M. Rubber–Filler Interactions and Network Structure in Relation to Stress–Strain Behavior of Vulcanized, Carbon Black Filled EPDM. Macromolecules 2011, 44, 4887–4900. [Google Scholar] [CrossRef]
- Mostafa, A.; Abouel-Kasem, A.; Bayoumi, M.R.; El-Sebaie, M.G. Rubber-filler interactions and its effect in rheological and mechanical properties of filled compounds. J. Test. Eval. 2010, 38, JTE101942. [Google Scholar]
- Ammari, F.; Dardouri, M.; Kahlaoui, M.; Meganem, F. Structure and Electrical Study of New Chemically Modified Poly(vinyl chloride). Int. J. Polym. Sci. 2015, 2015, 280325. [Google Scholar] [CrossRef]
- Hasan, N.; Pulst, M.; Samiullah, M.H.; Kressler, J. Comparison of Li+ -ion conductivity in linear and crosslinked poly(ethylene oxide). J. Polym. Sci. Part B Polym. Phys. 2019, 57, 21–28. [Google Scholar] [CrossRef] [Green Version]
- Kotobuki, M. Polymer electrolytes: State of the art. In Polymer Electrolytes: Characterization Techniques and Energy Applications; Winie, T., Arof, A.K., Thomas, S., Eds.; Wiley-VCH Verlag: Weinheim, Germany, 2020; pp. 1–21. [Google Scholar]
- Aziz, S.B.; Woo, T.J.; Kadir, M.; Ahmed, H.M. A conceptual review on polymer electrolytes and ion transport models. J. Sci. Adv. Mater. Devices 2018, 3, 1–17. [Google Scholar] [CrossRef]
- Roggero, A.; Caussé, N.; Dantras, E.; Villareal, L.; Santos, A.; Pébère, N. Thermal activation of impedance measurements on an epoxy coating for the corrosion protection: 1. dielectric spectroscopy response in the dry state. Electrochim. Acta 2019, 303, 239–245. [Google Scholar] [CrossRef] [Green Version]
- Morsy, R.; Ismaiel, M.; Yehia, A. Conductivity studies on acrylonitrile butadiene rubber loaded with different types of carbon blacks. Int. J. Mater. Methods Technol. 2013, 1, 22–35. [Google Scholar] [CrossRef]
- Cho, M.; Seo, H.; Nam, J.; Choi, H.; Koo, J.; Lee, Y. High ionic conductivity and mechanical strength of solid polymer electrolytes based on NBR/ionic liquid and its application to an electrochemical actuator. Sens. Actuators B Chem. 2007, 128, 70–74. [Google Scholar] [CrossRef]













| Composition | Neat NBR | NBR-H20 | NBR-H40 | NBR-H60 | NBR-M20 | NBR-M40 | NBR-M60 |
|---|---|---|---|---|---|---|---|
| KNB 35 L | 100 | 100 | 100 | 100 | 100 | 100 | 100 |
| ZnO | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 | 3.0 |
| St/A * | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 | 1.0 |
| HAF N330 | - | 20 | 40 | 60 | - | - | - |
| MT N990 | - | - | - | - | 20 | 40 | 60 |
| S | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 | 1.5 |
| TBBS + | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 | 0.7 |
| Composition | NBR-S20 | NBR-S40 | NBR-S60 |
|---|---|---|---|
| KBR 35 L | 100 | 100 | 100 |
| ZnO | 3.0 | 3.0 | 3.0 |
| St/A | 1.0 | 1.0 | 1.0 |
| Silica S-175 | 20 | 40 | 60 |
| Si-69 × | 1.6 | 3.2 | 4.8 |
| PEG # | 0.8 | 1.6 | 2.4 |
| S | 1.5 | 1.5 | 1.5 |
| TBBS + | 0.7 | 0.7 | 0.7 |
| Neat NBR | NBR H Series | NBR M Series | NBR S Series | |||||
|---|---|---|---|---|---|---|---|---|
| Contents (phr) | DRS (K) | DSC (K) | DRS (K) | DSC (K) | DRS (K) | DSC (K) | DRS (K) | DSC (K) |
| 0 | 250.0 ± 6.5 | 250.1 ± 0.2 | - | - | - | - | - | - |
| 20 | - | - | 247.8 ± 15.9 | 248.6 ± 0.2 | 247.5 ± 23.5 | 247.8 ± 0.2 | 252.6 ± 1.8 | 248.0 ± 0.1 |
| 40 | - | - | - | 249.2 ± 0.1 | 248.0 ± 20.8 | 248.8 ± 0.1 | 251.4 ± 4.2 | 249.6 ± 0.1 |
| 60 | - | - | - | 247.9 ± 0.1 | 251.6 ± 4.1 | 247.6 ± 0.1 | 251.7 ± 13.5 | 247.9 ± 0.1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kim, G.-H.; Moon, Y.-I.; Jung, J.-K.; Choi, M.-C.; Bae, J.-W. Influence of Carbon Black and Silica Fillers with Different Concentrations on Dielectric Relaxation in Nitrile Butadiene Rubber Investigated by Impedance Spectroscopy. Polymers 2022, 14, 155. https://doi.org/10.3390/polym14010155
Kim G-H, Moon Y-I, Jung J-K, Choi M-C, Bae J-W. Influence of Carbon Black and Silica Fillers with Different Concentrations on Dielectric Relaxation in Nitrile Butadiene Rubber Investigated by Impedance Spectroscopy. Polymers. 2022; 14(1):155. https://doi.org/10.3390/polym14010155
Chicago/Turabian StyleKim, Gyung-Hyun, Young-Il Moon, Jae-Kap Jung, Myung-Chan Choi, and Jong-Woo Bae. 2022. "Influence of Carbon Black and Silica Fillers with Different Concentrations on Dielectric Relaxation in Nitrile Butadiene Rubber Investigated by Impedance Spectroscopy" Polymers 14, no. 1: 155. https://doi.org/10.3390/polym14010155
APA StyleKim, G. -H., Moon, Y. -I., Jung, J. -K., Choi, M. -C., & Bae, J. -W. (2022). Influence of Carbon Black and Silica Fillers with Different Concentrations on Dielectric Relaxation in Nitrile Butadiene Rubber Investigated by Impedance Spectroscopy. Polymers, 14(1), 155. https://doi.org/10.3390/polym14010155