Compositional Influence on the Morphology and Thermal Properties of Woven Non-Woven Mats of PLA/OLA/MgO Electrospun Fibers
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
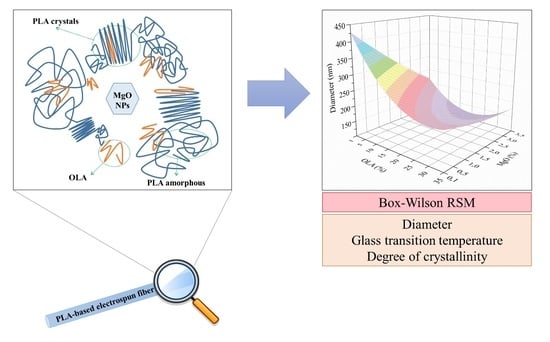
3.1. Influence of OLA and MgO NPs Content in the Average Diameter of the PLA-Based Efibers
3.2. Influence of OLA and MgO NPs Content in the Glass Transition Temperature of the PLA-Based Efibers
3.3. Influence of OLA and MgO NPs Content in the Degree of Crystallinity of the PLA-Based Efibers
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Singhvi, M.; Gokhale, D. Biomass to biodegradable polymer (PLA). RSC Adv. 2013, 3, 13558. [Google Scholar] [CrossRef]
- Nofar, M.; Sacligil, D.; Carreau, P.J.; Kamal, M.R.; Heuzey, M.-C. Poly (lactic acid) blends: Processing, properties and applications. Int. J. Biol. Macromol. 2019, 125, 307–360. [Google Scholar] [CrossRef] [PubMed]
- Rhim, J.-W.; Park, H.-M.; Ha, C.-S. Bio-nanocomposites for food packaging applications. Prog. Polym. Sci. 2013, 38, 1629–1652. [Google Scholar] [CrossRef]
- Raquez, J.M.; Habibi, Y.; Murariu, M.; Dubois, P. Polylactide (PLA)-based nanocomposites. Prog. Polym. Sci. 2013, 38, 1504–1542. [Google Scholar] [CrossRef]
- Farah, S.; Anderson, D.G.; Langer, R. Physical and mechanical properties of PLA, and their functions in widespread applications—A comprehensive review. Adv. Drug Deliv. Rev. 2016, 107, 367–392. [Google Scholar] [CrossRef] [Green Version]
- da Silva, D.; Kaduri, M.; Poley, M.; Adir, O.; Krinsky, N.; Shainsky-Roitman, J.; Schroeder, A. Biocompatibility, biodegradation and excretion of polylactic acid (PLA) in medical implants and theranostic systems. Chem. Eng. J. 2018, 340, 9–14. [Google Scholar] [CrossRef]
- Zaaba, N.F.; Jaafar, M. A review on degradation mechanisms of polylactic acid: Hydrolytic, photodegradative, microbial, and enzymatic degradation. Polym. Eng. Sci. 2020, 60, 2061–2075. [Google Scholar] [CrossRef]
- Leonés, A.; Sonseca, A.; López, D.; Fiori, S.; Peponi, L. Shape memory effect on electrospun PLA-based fibers tailoring their thermal response. Eur. Polym. J. 2019, 117, 217–226. [Google Scholar] [CrossRef]
- Darie-Niţă, R.N.; Vasile, C.; Irimia, A.; Lipşa, R.; Râpă, M. Evaluation of some eco-friendly plasticizers for PLA films processing. J. Appl. Polym. Sci. 2016, 133, 43223. [Google Scholar] [CrossRef]
- Leonés, A.; Lieblich, M.; Benavente, R.; Gonzalez, J.L.; Peponi, L. Potential applications of magnesium-based polymeric nanocomposites obtained by electrospinning technique. Nanomaterials 2020, 10, 1524. [Google Scholar] [CrossRef]
- Peponi, L.; Puglia, D.; Torre, L.; Valentini, L.; Kenny, J.M. Processing of nanostructured polymers and advanced polymeric based nanocomposites. Mater. Sci. Eng. R. Rep. 2014, 85, 1–46. [Google Scholar] [CrossRef] [Green Version]
- García-Martínez, J.M.; Areso, S.; Collar, E.P. The role of a novel p-phenylen-bis-maleamic acid grafted atactic polypropylene interfacial modifier in polypropylene/mica composites as evidenced by tensile properties. J. Appl. Polym. Sci. 2009, 113, 3929–3943. [Google Scholar] [CrossRef]
- Nofar, M.; Salehiyan, R.; Ray, S.S. Influence of nanoparticles and their selective localization on the structure and properties of polylactide-based blend nanocomposites. Compos. Part B Eng. 2021, 215, 108845. [Google Scholar] [CrossRef]
- Rahman, M.; Brazel, C.S. The plasticizer market: An assessment of traditional plasticizers and research trends to meet new challenges. Prog. Polym. Sci. 2004, 29, 1223–1248. [Google Scholar] [CrossRef]
- Bocqué, M.; Voirin, C.; Lapinte, V.; Caillol, S.; Robin, J.-J. Petro-based and bio-based plasticizers: Chemical structures to plasticizing properties. J. Polym. Sci. Part A Polym. Chem. 2016, 54, 11–33. [Google Scholar] [CrossRef]
- Satriyatama, A.; Rochman, V.A.A.; Adhi, R.E. Study of the Effect of Glycerol Plasticizer on the Properties of PLA/Wheat Bran Polymer Blends. IOP Conf. Ser. Mater. Sci. Eng. 2021, 1143, 012020. [Google Scholar] [CrossRef]
- Pivsa-Art, W.; Fujii, K.; Nomura, K.; Aso, Y.; Ohara, H.; Yamane, H. The effect of poly(ethylene glycol) as plasticizer in blends of poly(lactic acid) and poly(butylene succinate). J. Appl. Polym. Sci. 2016, 133, 43044. [Google Scholar] [CrossRef]
- Arrieta, M.P.; Peponi, L.; López, D.; Fernández-García, M. Recovery of yerba mate (Ilex paraguariensis) residue for the development of PLA-based bionanocomposite films. Ind. Crops Prod. 2018, 111, 317–328. [Google Scholar] [CrossRef]
- Salas-Papayanopolos, H.; Morales-Cepeda, A.B.; Sanchez, S.; Lafleur, P.G.; Gomez, I. Synergistic effect of silver nanoparticle content on the optical and thermo-mechanical properties of poly(l-lactic acid)/glycerol triacetate blends. Polym. Bull. 2017, 74, 4799–4814. [Google Scholar] [CrossRef]
- Burgos, N.; Tolaguera, D.; Fiori, S.; Jiménez, A. Synthesis and Characterization of Lactic Acid Oligomers: Evaluation of Performance as Poly(Lactic Acid) Plasticizers. J. Polym. Environ. 2014, 22, 227–235. [Google Scholar] [CrossRef] [Green Version]
- Cicogna, F.; Coiai, S.; De Monte, C.; Spiniello, R.; Fiori, S.; Franceschi, M.; Braca, F.; Cinelli, P.; Fehri, S.M.K.; Lazzeri, A.; et al. Poly(lactic acid) plasticized with low-molecular-weight polyesters: Structural, thermal and biodegradability features. Polym. Int. 2017, 66, 761–769. [Google Scholar] [CrossRef]
- Burgos, N.; Martino, V.P.; Jiménez, A. Characterization and ageing study of poly(lactic acid) films plasticized with oligomeric lactic acid. Polym. Degrad. Stab. 2013, 98, 651–658. [Google Scholar] [CrossRef]
- Arrieta, M.P.; López, J.; López, D.; Kenny, J.M.; Peponi, L. Development of flexible materials based on plasticized electrospun PLA-PHB blends: Structural, thermal, mechanical and disintegration properties. Eur. Polym. J. 2015, 73, 433–446. [Google Scholar] [CrossRef]
- Khorshidi, S.; Solouk, A.; Mirzadeh, H.; Mazinani, S.; Lagaron, J.M.; Sharifi, S.; Ramakrishna, S. A review of key challenges of electrospun scaffolds for tissue-engineering applications. J. Tissue Eng. Regen. Med. 2016, 10, 715–738. [Google Scholar] [CrossRef]
- Basar, A.O.; Castro, S.; Torres-Giner, S.; Lagaron, J.M.; Turkoglu Sasmazel, H. Novel poly(ε-caprolactone)/gelatin wound dressings prepared by emulsion electrospinning with controlled release capacity of Ketoprofen anti-inflammatory drug. Mater. Sci. Eng. C 2017, 81, 459–468. [Google Scholar] [CrossRef]
- Marina P Arrieta; Miguel Perdiguero; Stefano Fiori; José M Kenny; Laura Peponi Biodegradable electrospun PLA-PHB fibers plasticized with oligomeric lactic acid. Polym. Degrad. Stab. 2020, 179, 109226.
- Leonés, A.; Mujica-Garcia, A.; Arrieta, M.P.; Salaris, V.; Lopez, D.; Kenny, J.M.; Peponi, L. Organic and Inorganic PCL-Based Electrospun Fibers. Polymers 2020, 12, 1325. [Google Scholar] [CrossRef]
- Leonés, A.; Peponi, L.; Lieblich, M.; Benavente, R.; Fiori, S. In vitro degradation of plasticized PLA electrospun fiber mats: Morphological, thermal and crystalline evolution. Polymers 2020, 12, 2975. [Google Scholar] [CrossRef]
- Rodríguez-Sánchez, I.J.; Fuenmayor, C.A.; Clavijo-Grimaldo, D.; Zuluaga-Domínguez, C.M. Electrospinning of ultra-thin membranes with incorporation of antimicrobial agents for applications in active packaging: A review. Int. J. Polym. Mater. Polym. Biomater. 2021, 70, 1053–1076. [Google Scholar] [CrossRef]
- Arrieta, M.P.; López, J.; López, D.; Kenny, J.M.; Peponi, L. Effect of chitosan and catechin addition on the structural, thermal, mechanical and disintegration properties of plasticized electrospun PLA-PHB biocomposites. Polym. Degrad. Stab. 2016, 132, 145–156. [Google Scholar] [CrossRef]
- Dziemidowicz, K.; Sang, Q.; Wu, J.; Zhang, Z.; Zhou, F.; Lagaron, J.M.; Mo, X.; Parker, G.J.M.; Yu, D.-G.; Zhu, L.-M.; et al. Electrospinning for healthcare: Recent advancements. J. Mater. Chem. B 2021, 9, 939–951. [Google Scholar] [CrossRef] [PubMed]
- Mikos, A.G.; Temenoff, J.S. Formation of highly porous biodegradable scaffolds for tissue engineering. Electron. J. Biotechnol. 2000, 3, 1995–2000. [Google Scholar] [CrossRef]
- Zhu, G.; Zhang, T.; Chen, M.; Yao, K.; Huang, X.; Zhang, B.; Li, Y.; Liu, J.; Wang, Y.; Zhao, Z. Bone physiological microenvironment and healing mechanism: Basis for future bone-tissue engineering scaffolds. Bioact. Mater. 2021, 6, 4110–4140. [Google Scholar] [CrossRef] [PubMed]
- Leonés, A.; Salaris, V.; Mujica-Garcia, A.; Arrieta, M.P.; Lopez, D.; Lieblich, M.; Kenny, J.M.; Peponi, L. PLA Electrospun Fibers Reinforced with Organic and Inorganic Nanoparticles: A Comparative Study. Molecules 2021, 26, 4925. [Google Scholar] [CrossRef] [PubMed]
- Ferrández-Montero, A.; Lieblich, M.; González-Carrasco, J.L.; Benavente, R.; Lorenzo, V.; Detsch, R.; Boccaccini, A.R.; Ferrari, B. Development of biocompatible and fully bioabsorbable PLA/Mg films for tissue regeneration applications. Acta Biomater. 2019, 98, 114–124. [Google Scholar] [CrossRef] [PubMed]
- Boakye, M.; Rijal, N.; Adhikari, U.; Bhattarai, N. Fabrication and Characterization of Electrospun PCL-MgO-Keratin-Based Composite Nanofibers for Biomedical Applications. Materials 2015, 8, 4080–4095. [Google Scholar] [CrossRef]
- De Silva, R.T.; Mantilaka, M.M.M.G.P.G.; Goh, K.L.; Ratnayake, S.P.; Amaratunga, G.A.J.; de Silva, K.M.N. Magnesium Oxide Nanoparticles Reinforced Electrospun Alginate-Based Nanofibrous Scaffolds with Improved Physical Properties. Int. J. Biomater. 2017, 2017, 1–9. [Google Scholar] [CrossRef]
- Cramariuc, B.; Cramariuc, R.; Scarlet, R.; Manea, L.R.; Lupu, I.G.; Cramariuc, O. Fiber diameter in electrospinning process. J. Electrostat. 2013, 71, 189–198. [Google Scholar] [CrossRef]
- El-hadi, A.; Al-Jabri, F. Influence of Electrospinning Parameters on Fiber Diameter and Mechanical Properties of Poly(3-Hydroxybutyrate) (PHB) and Polyanilines (PANI) Blends. Polymers 2016, 8, 97. [Google Scholar] [CrossRef] [Green Version]
- Martínez, J.M.G.; Collar, E.P. On the combined effect of both the reinforcement and a waste based interfacial modifier on the matrix glass transition in ipp/a-pp-ppbma/mica composites. Polymers 2020, 12, 1–13. [Google Scholar]
- García-Martínez, J.-M.; Collar, E.P. The Role of a Succinyl Fluorescein-Succinic Anhydride Grafted Atactic Polypropylene on the Dynamic Mechanical Properties of Polypropylene/Polyamide-6 Blends at the Polypropylene Glass Transition. Polymers 2020, 12, 1216. [Google Scholar] [CrossRef]
- Fisher, R.A. The Desing of Experiments, 1st ed.; Hafner: New York, NY, USA, 1960. [Google Scholar]
- Box, G.E.P.; Hunter, W.G.; Hunter, J.S. Response surface methods. In Statistics for Experimenters, 1st ed.; Wiley & Sons: New York, NY, USA, 1978. [Google Scholar]
- Arrieta, M.P.; Gil, A.L.; Yusef, M.; Kenny, J.M.; Peponi, L. Electrospinning of PCL-based blends: Processing optimization for their scalable production. Materials 2020, 13, 3853. [Google Scholar] [CrossRef]
- Peponi, L.; Navarro-Baena, I.; Báez, J.E.; Kenny, J.M.; Marcos-Fernández, A. Effect of the molecular weight on the crystallinity of PCL-b-PLLA di-block copolymers. Polymer 2012, 53, 4561–4568. [Google Scholar] [CrossRef] [Green Version]
- Manea, L.R.; Bertea, A.-P.; Nechita, E.; Popescu, C.V. Mathematical Modeling of the Relation between Electrospun Nanofibers Characteristics and the Process Parameters. In Electrospinning Method Used to Create Functional Nanocomposites Films; InTech: London, UK, 2018; p. 13. [Google Scholar]
- Piñeiro, G.; Perelman, S.; Guerschman, J.P.; Paruelo, J.M. How to evaluate models: Observed vs. predicted or predicted vs. observed? Ecol. Modell. 2008, 216, 316–322. [Google Scholar] [CrossRef]
- Liu, C.; Shen, J.; Liao, C.Z.; Yeung, K.W.K.; Tjong, S.C. Novel electrospun polyvinylidene fluoride-graphene oxide-silver nanocomposite membranes with protein and bacterial antifouling characteristics. Express Polym. Lett. 2018, 12, 365–382. [Google Scholar] [CrossRef]
- Kathrein, H.; Freund, F. Electrical conductivity of magnesium oxide single crystal below 1200 K. J. Phys. Chem. Solids 1983, 44, 177–186. [Google Scholar] [CrossRef]
- Habeeb, M.A.; Hamza, R.S.A. Synthesis of (Polymer blend-MgO) nanocomposites and studying electrical properties for piezoelectric application. Indones. J. Electr. Eng. Inform. 2018, 6, 428–435. [Google Scholar]
- Khan, R.A.A.; Qi, H.-K.; Huang, J.-H.; Luo, M.-B. A simulation study on the effect of nanoparticle size on the glass transition temperature of polymer nanocomposites. Soft Matter 2021, 17, 8095–8104. [Google Scholar] [CrossRef]
- Serenko, O.A.; Roldughin, V.I.; Askadskii, A.D.; Serkova, E.S.; Strashnov, P.V.; Shifrina, Z.B. The effect of size and concentration of nanoparticles on the glass transition temperature of polymer nanocomposites. RSC Adv. 2017, 7, 50113–50120. [Google Scholar] [CrossRef] [Green Version]
- Papageorgiou, G.Z.; Achilias, D.S.; Bikiaris, D.N.; Karayannidis, G.P. Crystallization kinetics and nucleation activity of filler in polypropylene/surface-treated SiO2 nanocomposites. Thermochim. Acta 2005, 427, 117–128. [Google Scholar] [CrossRef]
- Shi, X.; Zhang, G.; Phuong, T.V.; Lazzeri, A. Synergistic effects of nucleating agents and plasticizers on the crystallization behavior of Poly(lactic acid). Molecules 2015, 20, 1579–1593. [Google Scholar] [CrossRef]
- Clarkson, C.M.; El Awad Azrak, S.M.; Schueneman, G.T.; Snyder, J.F.; Youngblood, J.P. Crystallization kinetics and morphology of small concentrations of cellulose nanofibrils (CNFs) and cellulose nanocrystals (CNCs) melt-compounded into poly(lactic acid) (PLA) with plasticizer. Polymer 2020, 187, 122101. [Google Scholar] [CrossRef]






| Run | Coded Factors | Controlled Factors | ||
|---|---|---|---|---|
| OLA | MgO | OLA (wt%) | MgO (wt%) | |
| I | −1 | −1 | 6.00 | 0.60 |
| II | 1 | −1 | 30.00 | 0.60 |
| III | −1 | 1 | 6.00 | 3.00 |
| IV | 1 | 1 | 30.00 | 3.00 |
| V | −√2 | 0 | 1.03 | 1.80 |
| VI | √2 | 0 | 34.97 | 1.80 |
| VII | 0 | −√2 | 18.00 | 0.10 |
| VIII | 0 | √2 | 18.00 | 3.49 |
| IX | 0 | 0 | 18.00 | 1.80 |
| X | 0 | 0 | 18.00 | 1.80 |
| XI | 0 | 0 | 18.00 | 1.80 |
| XII | 0 | 0 | 18.00 | 1.80 |
| XIII | 0 | 0 | 18.00 | 1.80 |
| Run | Diameter (nm) | Tg (°C) | Xc (%) |
|---|---|---|---|
| I | 469 ± 106 | 57 | 3.9 |
| II | 316 ± 67 | 31 | 30.0 |
| III | 137 ± 16 | 56 | 9.6 |
| IV | 156 ± 38 | 32 | 17.6 |
| V | 438 ± 67 | 51 | 3.3 |
| VI | 188 ± 45 | 34 | 16.6 |
| VII | 192 ± 39 | 43 | 9.8 |
| VIII | 186 ± 56 | 46 | 8.4 |
| IX | 172 ± 35 | 42 | 6.1 |
| X | 187 ± 43 | 44 | 14.6 |
| XI | 205 ± 62 | 43 | 12.3 |
| XII | 162 ± 42 | 47 | 7.7 |
| XIII | 163 ± 36 | 43 | 8.6 |
| <r2> (%) | L. F. * (%) | C. F. * (%) | Ind. T. * | L. T. * | Int. T. * | Q. T. * | |||
|---|---|---|---|---|---|---|---|---|---|
| a0 | a1 | a2 | a3 | a4 | a5 | ||||
| Diameter (nm) | 73.76 | 1.5 | 94.1 | 645.3 | −28.51 | −131.4 | 2.986 | 0.5016 | 7.101 |
| Tg (°C) | 88.59 | 5.2 | 99.1 | 57.86 | −0.7364 | −1.113 | 0.03993 | −0.003420 | 0.3004 |
| Xc (%) | 75.61 | 18.9 | 95.1 | −2.816 | 0.7388 | 2.096 | −0.3142 | 0.01046 | 0.7352 |
| Ind. T. * | L. T. * | Int. T. * | Q. T. * | |||
|---|---|---|---|---|---|---|
| x1 | x2 | x1·x2 | x12 | x22 | ||
| Diameter (nm) | 5.31 (99.7%) | 3.33 (98.6%) | 1.54 (82.8%) | 1.18 (71.0%) | 2.61 (96.6%) | 0.37 (31.1%) |
| Tg (°C) | 9.51 (99.9%) | 1.72 (87.0%) | 0.26 (26.0%) | 0.31 (28.5%) | 0.36 (30.5%) | 0.31 (28.4%) |
| Xc (%) | 0.37 (31.0%) | 1.37 (77.8%) | 0.39 (32.0%) | 1.96 (91.1%) | 0.86 (56.6%) | 0.61 (43.3%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Leonés, A.; Peponi, L.; García-Martínez, J.-M.; Collar, E.P. Compositional Influence on the Morphology and Thermal Properties of Woven Non-Woven Mats of PLA/OLA/MgO Electrospun Fibers. Polymers 2022, 14, 2092. https://doi.org/10.3390/polym14102092
Leonés A, Peponi L, García-Martínez J-M, Collar EP. Compositional Influence on the Morphology and Thermal Properties of Woven Non-Woven Mats of PLA/OLA/MgO Electrospun Fibers. Polymers. 2022; 14(10):2092. https://doi.org/10.3390/polym14102092
Chicago/Turabian StyleLeonés, Adrián, Laura Peponi, Jesús-María García-Martínez, and Emilia P. Collar. 2022. "Compositional Influence on the Morphology and Thermal Properties of Woven Non-Woven Mats of PLA/OLA/MgO Electrospun Fibers" Polymers 14, no. 10: 2092. https://doi.org/10.3390/polym14102092
APA StyleLeonés, A., Peponi, L., García-Martínez, J. -M., & Collar, E. P. (2022). Compositional Influence on the Morphology and Thermal Properties of Woven Non-Woven Mats of PLA/OLA/MgO Electrospun Fibers. Polymers, 14(10), 2092. https://doi.org/10.3390/polym14102092