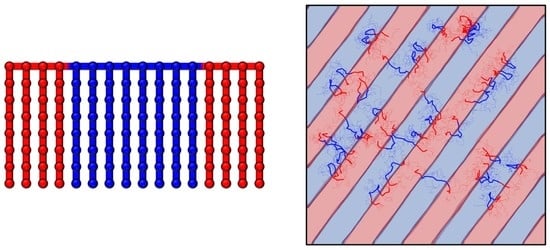
Loop and Bridge Conformations of ABA Triblock Comb Copolymers: A Conformational Assessment for Molecular Composites
Abstract
:1. Introduction
2. Simulation Methods
3. Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Holden, G.L.; Legge, N.R.; Quirk, R.P.; Schroeder, H.E. Thermoplastic Elastomers; Hanser: Munich, Germany, 1996. [Google Scholar]
- Ding, W.; Wang, S.; Yao, K.; Ganewatta, M.S.; Tang, C.; Robertson, M.L. Physical Behavior of Triblock Copolymer Thermoplastic Elastomers Containing Sustainable Rosin-Derived Polymethacrylate End Blocks. ACS Sustain. Chem. Eng. 2017, 5, 11470–11480. [Google Scholar] [CrossRef]
- Gregory, G.L.; Sulley, G.S.; Carrodeguas, L.P.; Chen, T.P.D.; Santmarti, A.; Terrill, N.J.; Lee, K.Y.; Williams, C.K. Triblock Polyester Thermoplastic Elastomers with Semi-Aromatic Polymer End Blocks by Ring-Opening Copolymerization. Chem. Sci. 2020, 11, 6567–6581. [Google Scholar] [CrossRef]
- Jia, M.; Zhang, D.; de Kort, G.W.; Wilsens, C.H.R.M.; Rastogi, S.; Hadjichristidis, N.; Gnanou, Y.; Feng, X. All-Polycarbonate Thermoplastic Elastomers Based on Triblock Copolymers Derived from Triethylborane-Mediated Sequential Copolymerization of CO2 with Various Epoxides. Macromolecules 2020, 53, 5297–5307. [Google Scholar] [CrossRef] [PubMed]
- Kalita, U.; Samanta, S.; Banerjee, S.L.; Das, N.C.; Singha, N.K. Biobased Thermoplastic Elastomer Based on an SMS Triblock Copolymer Prepared via RAFT Polymerization in Aqueous Medium. Macromolecules 2021, 54, 1478–1488. [Google Scholar] [CrossRef]
- Kawarazaki, I.; Hayashi, M. Enhancement of Mechanical Properties of ABA Triblock CopolymerBased Elastomers by Incorporating Partial Cross-Links on the Soft Bridge Chains. ACS Appl. Polym. Mater. 2021, 3, 1271–1275. [Google Scholar] [CrossRef]
- Wu, H.; Thakur, V.K.; Kessler, M.R. Novel Low-Cost Hybrid Composites from Asphaltene/SBS Triblock Copolymer with Improved Thermal and Mechanical Properties. J. Mater. Sci. 2016, 51, 2394–2403. [Google Scholar] [CrossRef]
- Thakur, V.K.; Grewell, D.; Thunga, M.; Kessler, M.R. Novel Composites from Eco-Friendly SoyFlour/SBS Triblock Copolymer. Macromol. Mater. Eng. 2014, 299, 953–958. [Google Scholar] [CrossRef]
- Zhang, Y.; Chen, S.; Zhang, H.; Ding, X.; Fu, P.; Du, F. Fabrication of Conjugated Triblock Copolymer/Single-Walled Carbon Nanotubes Composite Films with Enhanced Thermoelectric Performance. Compos. Commun. 2021, 27, 10083. [Google Scholar] [CrossRef]
- Watanabe, H.; Sato, T.; Osaki, K.; Yao, M.L.; Yamagishi, A. Rheological and Dielectric Behavior of a Styrene-Isoprene-Styrene Triblock Copolymer in Selective Solvents. 2. Contribution of Loop-Type Middle Blocks to Elasticity and Plasticity. Macromolecules 1997, 30, 5877–5892. [Google Scholar] [CrossRef]
- Honeker, C.C.; Thomas, E.L. Impact of Morphological Orientation in Determining Mechanical Properties in Triblock Copolymer Systems. Chem. Mater. 1996, 8, 1702–1714. [Google Scholar] [CrossRef]
- Takano, A.; Kamaya, I.; Takahashi, Y.; Matsushita, Y. Effect of Loop/Bridge Conformation Ratio on Elastic Properties of the Sphere-Forming ABA Triblock Copolymers: Preparation of Samples and Determination of Loop/Bridge Ratio. Macromolecules 2005, 38, 9718–9723. [Google Scholar] [CrossRef]
- Milner, S.T.; Witten, T.A. Bridging Attraction by Telechelic Polymers. Macromolecules 1992, 25, 5495–5503. [Google Scholar] [CrossRef]
- Watanabe, H. Slow Dielectric Relaxation of a Styrene—Isoprene—Styrene Triblock Copolymer with Dipole Inversion in the Middle Block: A Challenge to a Loop/Bridge Problem. Macromolecules 1995, 28, 5006–5011. [Google Scholar] [CrossRef]
- Karatasos, K.; Anastasiadis, S.H.; Pakula, T.; Wayanabe, H. On the Loops-to-Bridges Ratio in Ordered Triblock Copolymers: An Investigation by Dielectric Relaxation Spectroscopy and Computer Simulations. Macromolecules 2000, 33, 523–541. [Google Scholar] [CrossRef]
- Mori, Y.; Lim, L.S.; Bates, F.S. Consequences of Molecular Bridging in Lamellae-Forming Triblock/Pentablock Copolymer Blends. Macromolecules 2003, 36, 9879–9898. [Google Scholar] [CrossRef]
- Zhulina, E.B.; Halperin, A. Lamellar Mesogels and Mesophases: A Self-Consistent-Field Theory. Macromolecules 1992, 25, 5730–5741. [Google Scholar] [CrossRef]
- Avalas, J.B.; Johner, A.; Joanny, J.F. Bridging by Adsorbed Polymers Between Two Surfaces. J. Chem. Phys. 1994, 101, 9181–9194. [Google Scholar] [CrossRef]
- Matsen, M.W.; Schick, M. Lamellar Phase of a Symmetric Triblock Copolymer. Macromolecules 1994, 27, 187–192. [Google Scholar] [CrossRef]
- Huh, J.; Jo, W.H.; Brinke, G.T. Conformational Analysis in ABA Triblock Melts by Monte Carlo Simulation. Macromolecules 2002, 35, 2413–2416. [Google Scholar] [CrossRef] [Green Version]
- Aoyagi, T.; Honda, T.; Doi, M. Microstructural Study of Mechanical Properties of the ABA Triblock Copolymer Using Self-Consistent Field and Molecular Dynamics. J. Chem. Phys. 2002, 117, 8153–8161. [Google Scholar] [CrossRef]
- Abu-Sharkh, B.; AlSunaidi, A. Morphology and Conformation Analysis of Self-Assembled Triblock Copolymer Melts. Macromol. B Theory Simul. 2006, 15, 507–515. [Google Scholar] [CrossRef]
- Morita, H.; Miyamoto, A.; Kotani, M. Recoverably and Destructively Deformed Domain Structures in Elongation Process of Thermoplastic Elastomer Analyzed by Graph Theory. Polymer 2020, 188, 122098. [Google Scholar] [CrossRef]
- Gu, W.; Huh, J.; Hong, S.W.; Sveinbjornsson, B.R.; Park, C.; Grubbs, R.H.; Russell, T.P. Self-Assembly of Symmetric Brush Diblock Copolymers. ACS Nano 2013, 7, 2551–2558. [Google Scholar] [CrossRef] [Green Version]
- Rzayev, J. Synthesis of Polystyrene-Polylactide Bottlebrush Block Copolymers and Their Melt Self-Assembly into Large Domain Nanostructures. Macromolecules 2009, 42, 2135–2141. [Google Scholar] [CrossRef]
- Bolton, J.; Bailey, T.S.; Rzayev, J. Large Pore Size Nanoporous Materials from the Self-Assembly of Asymmetric Bottlebrush Block Copolymers. Nano Lett. 2011, 11, 998–1001. [Google Scholar] [CrossRef]
- Fenyves, R.; Schmutz, M.; Horner, I.J.; Bright, F.V.; Rzayev, J. Aqueous Self-Assembly of Giant Bottlebrush Block Copolymer Surfactants as Shape-Tunable Building Blocks. J. Am. Chem. Soc. 2014, 136, 7762–7770. [Google Scholar] [CrossRef]
- Song, D.P.; Zhao, T.H.; Guidetti, G.; Vignolini, S.; Parker, R.M. Hierarchical Photonic Pigments via the Confined Self-Assembly of Bottlebrush Block Copolymers. ACS Nano 2019, 13, 1764–1771. [Google Scholar] [CrossRef] [Green Version]
- Kim, E.J.; Shin, J.J.; Do, T.; Lee, G.S.; Park, J.; Thapar, V.; Choi, J.; Bang, J.; Yi, G.R.; Hur, S.M.; et al. Molecular Weight Dependent Morphological Transitions of Bottlebrush Block Copolymer Particles: Experiments and Simulations. ACS Nano 2021, 15, 5513–5522. [Google Scholar] [CrossRef]
- Yang, J.X.; Long, Y.Y.; Pan, L.; Men, Y.F.; Li, Y.S. Spontaneously Healable Thermoplastic Elastomers Achieved through One-Pot Living Ring-Opening Metathesis Copolymerization of Well-Designed Bulky Monomers. ACS Appl. Mater. Interfaces 2016, 8, 12445–12455. [Google Scholar] [CrossRef]
- Sunday, D.F.; Chang, A.B.; Liman, C.D.; Gann, E.; Delongchamp, D.M.; Thomsen, L.; Matsen, M.W.; Grubbs, R.H.; Soles, C.L. Self-Assembly of ABC Bottlebrush Triblock Terpolymers with Evidence for Looped Backbone Conformations. Macromolecules 2018, 51, 7178–7185. [Google Scholar] [CrossRef]
- Nian, S.; Lian, H.; Gong, Z.; Zhernenkov, M.; Qin, J.; Cai, L.H. Molecular Architecture Directs Linear-Bottlebrush-Linear Triblock Copolymers to Self-Assemble to Soft Reprocessable Elastomers. ACS Macro Lett. 2019, 8, 1528–1534. [Google Scholar] [CrossRef]
- Español, P.; Warren, P.B. Statistical Mechanics of Dissipative Particle Dynamics. Europhys. Lett. 1995, 30, 191–196. [Google Scholar] [CrossRef] [Green Version]
- Groot, R.D.; Warren, P.B. Dissipative Particle Dynamics: Bridging the Gap between Atomistic and Mesoscopic Simulation. J. Chem. Phys. 1997, 107, 4423–4435. [Google Scholar] [CrossRef]
- Andersona, J.A.; Glaser, J.; Glotzer, S.C. HOOMD-blue: A Python Package for High-Performance Molecular Dynamics and Hard Particle Monte Carlo Simulations. Comput. Mater. Sci. 2020, 173, 109363. [Google Scholar] [CrossRef] [Green Version]
- Groot, R.D.; Madden, T.J. Dynamic Simulation of Diblock Copolymer Microphase Separation. J. Chem. Phys. 1998, 108, 8713–8724. [Google Scholar] [CrossRef]
- Spenley, N.A. Scaling Laws for Polymers in Dissipative Particle Dynamics. Europhys. Lett. 2000, 49, 534–540. [Google Scholar] [CrossRef]
- Phillips, C.L.; Anderson, J.A.; Glotzer, S.C. Pseudo-Random Number Generation for Brownian Dynamics and Dissipative Particle Dynamics Simulations on GPU Devices. J. Comput. Phys. 2011, 230, 7191–7201. [Google Scholar] [CrossRef]
- Allen, M.P.; Tildesley, D.J. Computer Simulation of Liquids, 2nd ed.; Clarendon Press: Oxford, UK, 2017. [Google Scholar]
- Karabin, M.; Stuartb, S.J. Simulated Annealing with Adaptive Cooling Rates. J. Chem. Phys. 2020, 153, 114103. [Google Scholar] [CrossRef]
- Bishop, M.; Frinks, S. Error Analysis in Computer Simulations. J. Chem. Phys. 2020, 87, 3675–3676. [Google Scholar] [CrossRef]
- Mikhailov, I.V.; Leermakers, F.A.; Darinskii, A.A.; Zhulina, E.B.; Borisov, O.V. Theory of microphase segregation in ABA triblock comb-shaped copolymers: Lamellar mesophase. Macromolecules 2021, 54, 4747–4759. [Google Scholar] [CrossRef]




| Parameter | Value | Unit 1 | Equations |
|---|---|---|---|
| 25.0 | (2) | ||
| 4.5 | (3) and (4) | ||
| K | 100.0 | (6) | |
| 0.7 | (6) |
| Architecure | M | N | L1 | |
|---|---|---|---|---|
| L-TBC | 48 | 1 | 1.08 | 8.26 ± 0.19 |
| C-TBC | 32 | 2 | 0.99 | 8.18 ± 0.26 |
| C-TBC | 24 | 4 | 0.77 | 8.17 ± 0.16 |
| C-TBC | 16 | 8 | 0.72 | 8.26 ± 0.18 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Jung, J.-Y.; Shin, H.-W.; Park, J.-W.; Bang, J.; Huh, J. Loop and Bridge Conformations of ABA Triblock Comb Copolymers: A Conformational Assessment for Molecular Composites. Polymers 2022, 14, 2301. https://doi.org/10.3390/polym14112301
Park J, Jung J-Y, Shin H-W, Park J-W, Bang J, Huh J. Loop and Bridge Conformations of ABA Triblock Comb Copolymers: A Conformational Assessment for Molecular Composites. Polymers. 2022; 14(11):2301. https://doi.org/10.3390/polym14112301
Chicago/Turabian StylePark, Jihoon, Je-Yeon Jung, Hyun-Woo Shin, Jong-Wan Park, Joona Bang, and June Huh. 2022. "Loop and Bridge Conformations of ABA Triblock Comb Copolymers: A Conformational Assessment for Molecular Composites" Polymers 14, no. 11: 2301. https://doi.org/10.3390/polym14112301
APA StylePark, J., Jung, J.-Y., Shin, H.-W., Park, J.-W., Bang, J., & Huh, J. (2022). Loop and Bridge Conformations of ABA Triblock Comb Copolymers: A Conformational Assessment for Molecular Composites. Polymers, 14(11), 2301. https://doi.org/10.3390/polym14112301