Equilibrium and Dynamic Surface Tension Behavior in Colloidal Unimolecular Polymers (CUP)
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Synthesis
2.2. Surface Tension Measurements
2.3. Thermogravimetric Analysis Measurements
3. Results and Discussion
3.1. Polymer Synthesis and Characterization
3.2. Particle Size Analysis and Charge Density
3.3. Equilibrium Surface Tension Behavior
3.4. Model for CUP Particles at Interface
3.5. Relationship between Surface Tension and Charge Groups, Based on Model A
3.6. Surface Tension at Higher Concentration
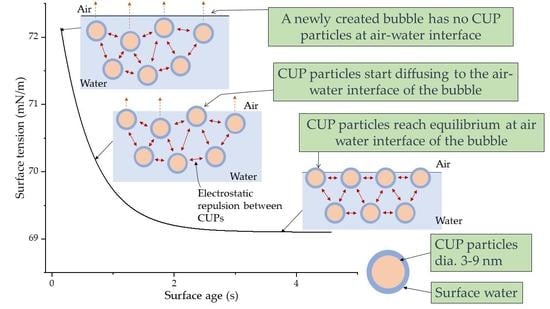
3.7. Dynamic Surface Tension Behavior
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Binks, B.P. Particles as surfactants—Similarities and differences. Curr. Opin. Colloid Interface Sci. 2002, 7, 21–41. [Google Scholar] [CrossRef]
- Hunter, T.N.; Pugh, R.J.; Franks, G.V.; Jameson, G.J. The role of particles in stabilising foams and emulsions. Adv. Colloid Interface Sci. 2008, 137, 57–81. [Google Scholar] [CrossRef]
- Menon, V.B.; Wasan, D.T. Particle—Fluid interactions with application to solid-stabilized emulsions part I. The effect of asphaltene adsorption. Colloids Surf. 1986, 19, 89–105. [Google Scholar] [CrossRef]
- Levine, S.; Bowen, B.D.; Partridge, S.J. Stabilization of emulsions by fine particles I. Partitioning of particles between continuous phase and oil/water interface. Colloids Surf. 1989, 38, 325–343. [Google Scholar] [CrossRef]
- Marquez, M.; Grady, B.P. The use of surface tension to predict the formation of 2D arrays of latex spheres formed via the langmuir–blodgett-like technique. Langmuir 2004, 20, 10998–11004. [Google Scholar] [CrossRef]
- Binks, B.P.; Lumsdon, S.O. Stability of oil-in-water emulsions stabilized by silica particles. Phys. Chem. Chem. Phys. 1999, 1, 3007–3016. [Google Scholar] [CrossRef]
- Rousseau, D. Fat crystals and emulsion stability—A review. Food Res. Int. 2000, 33, 3–14. [Google Scholar] [CrossRef]
- Binks, B.P.; Lumsdon, S.O. Influence of particle wettability on the type and stability of surfactant-free emulsions. Langmuir 2000, 16, 8622–8631. [Google Scholar] [CrossRef]
- Okubo, T. Surface tension of structured colloidal suspensions of polystyrene and silica spheres at the air-water interface. J. Colloid Interface Sci. 1995, 171, 55–62. [Google Scholar] [CrossRef]
- Riddles, C.; Zhao, W.; Hu, H.J.; Chen, M.; Van De Mark, M.R. Self-assembly of Water Insoluble Polymers into Colloidal Unimolecular Polymer (CUP) Particles of 3–9 nm. Polymer 2013, 55, 48–57. [Google Scholar] [CrossRef]
- Van De Mark, M.R.; Natu, A.; Gade, S.V.; Chen, M.; Hancock, C.; Riddles, C. Molecular Weight (Mn) and Functionality Effects on CUP Formation and Stability. J. Coat. Technol. Res. 2014, 11, 111–122. [Google Scholar] [CrossRef]
- Zore, A.; Geng, P.; Zhang, Y.; Van De Mark, M.R. Defining the Collapse Point in Colloidal Unimolecular Polymer (CUP) Formation. Polymers 2022, 14, 1909. [Google Scholar] [CrossRef]
- Geng, P.; Zore, A.; Van De Mark, M.R. Thermodynamic Characterization of Free and Surface Water of Colloidal Unimolecular Polymer (CUP) Particles Utilizing DSC. Polymers 2020, 12, 1417. [Google Scholar] [CrossRef] [PubMed]
- Dawib, Y.A. NMR T1 Studies of Colloidal Unimolecular Polymer (CUP) Surface Water. Ph.D. Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 2015. [Google Scholar]
- Chen, M.; Riddles, C.; Van De Mark, M. Gel point behavior of colloidal unimolecular polymer (CUP) particles. Colloid Polym. Sci. 2013, 291, 2893–2901. [Google Scholar] [CrossRef]
- Chen, M.; Riddles, C.J.; Van De Mark, M.R. Electroviscous contribution to the rheology of colloidal unimolecular polymer (CUP) particles in water. Langmuir 2013, 29, 14034–14043. [Google Scholar] [CrossRef]
- Mistry, J.K.; Van De Mark, M.R. Aziridine cure of acrylic colloidal unimolecular polymers (CUPs). J. Coat. Technol. Res. 2013, 10, 453–463. [Google Scholar] [CrossRef]
- Mistry, J.K.; Natu, A.M.; Van De Mark, M.R. Synthesis and application of acrylic colloidal unimolecular polymers as a melamine thermoset system. J. Appl. Polym. Sci. 2014, 131, 40916. [Google Scholar] [CrossRef]
- Natu, A.M. Synthesis, Characterization and Application of Acrylic Colloidal Unimolecular Polymer (CUP). Ph.D. Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 2015. [Google Scholar]
- Natu, A.; Van De Mark, M.R. Synthesis and characterization of an acid catalyst for acrylic-melamine resin systems based on colloidal unimolecular polymer (CUP) particles of MMA-AMPS. Prog. Org. Coat. 2015, 81, 35–46. [Google Scholar] [CrossRef]
- Natu, A.M.; Wiggins, M.; Van De Mark, M.R. Synthesis and characterization of cationic colloidal unimolecular polymer (CUP) particles. Colloid Polym. Sci. 2015, 293, 1191–1204. [Google Scholar] [CrossRef]
- Gade, S.V. Application of Colloidal Unimolecular Polymer (CUP) Particles in Coatings. Ph.D. Thesis, Missouri University of Science and Technology, Rolla, MO, USA, 2015. [Google Scholar]
- Okubo, T. Surface tension of synthetic polyelectrolyte solutions at the air-water interface. J. Colloid Interface Sci. 1988, 125, 386–398. [Google Scholar] [CrossRef]
- Millet, F.; Nedyalkov, M.; Renard, B.; Perrin, P.; Lafuma, F.; Benattar, J. Adsorption of Hydrophobically Modified Poly(acrylic acid) Sodium Salt at the Air/Water Interface by Combined Surface Tension and X-ray Reflectivity Measurements. Langmuir 1999, 15, 2112–2119. [Google Scholar] [CrossRef]
- Ishimuro, Y.; Ueberreiter, K. The surface tension of poly (acrylic acid) in sodium chloride solutions. Colloid Polym. Sci. 1980, 258, 1052–1054. [Google Scholar] [CrossRef]
- Dong, L.; Johnson, D.T. The study of the surface tension of charge-stabilized colloidal dispersions. J. Dispers. Sci. Technol. 2005, 25, 575–583. [Google Scholar] [CrossRef]
- Dong, L.; Johnson, D. Interfacial tension measurements of colloidal suspensions: An explanation of colloidal particle-driven interfacial flows. Adv. Space Res. 2003, 32, 149–153. [Google Scholar] [CrossRef]
- Dong, L.; Johnson, D. Surface tension of charge-stabilized colloidal suspensions at the water-air interface. Langmuir 2003, 19, 10205–10209. [Google Scholar] [CrossRef]
- Paunov, V.N.; Binks, B.P.; Ashby, N.P. Adsorption of charged colloid particles to charged liquid surfaces. Langmuir 2002, 18, 6946–6955. [Google Scholar] [CrossRef]
- Vafaei, S.; Purkayastha, A.; Jain, A.; Ramanath, G.; Borca-Tasciuc, T. The effect of nanoparticles on the liquid–gas surface tension of Bi2Te3 nanofluids. Nanotechnology 2009, 20, 185702. [Google Scholar] [CrossRef]
- Tanvir, S.; Qiao, L. Surface tension of nanofluid-type fuels containing suspended nanomaterials. Nanoscale Res. Lett. 2012, 7, 226. [Google Scholar] [CrossRef] [Green Version]
- Zore, A.; Van De Mark, M. Surface Tension Studies in Colloidal Unimolecular Polymers. CoatingsTech 2021, 18, 24–31. [Google Scholar]
- Geng, P.; Zore, A.; Van De Mark, M.R. Investigation of the Evaporation Rate of Water from Colloidal Unimolecular Polymer (CUP) Systems by Isothermal TGA. Polymers 2020, 12, 2752. [Google Scholar] [CrossRef] [PubMed]
- Fainerman, V.B.; Miller, R. Maximum bubble pressure tensiometry—An analysis of experimental constraints. Adv. Colloid Interface Sci. 2004, 108, 287–301. [Google Scholar] [CrossRef]
- Fainerman, V.B.; Miller, R.; Joos, P. The measurement of dynamic surface tension by the maximum bubble pressure method. Colloid Polym. Sci. 1994, 272, 731–739. [Google Scholar] [CrossRef]
- Mysels, K.J. Improvements in the maximum-bubble-pressure method of measuring surface tension. Langmuir 1986, 2, 428–432. [Google Scholar] [CrossRef]
- Fainerman, V.B.; Miller, R.; Aksenenko, E.V.; Makievski, A.V. Equilibrium adsorption properties of single and mixed surfactant solutions. In Surfactants: Chemistry, Interfacial Properties, Applications, 1st ed.; Fainerman, V.B., Mobius, D., Miller, R., Eds.; Elsevier: Amsterdam, The Netherlands, 2001; pp. 189–286. [Google Scholar]
- Le, T.T.Y.; Hussain, S.; Tsay, R.Y.; Noskov, B.A.; Akentiev, A.; Lin, S.Y. On the equilibrium surface tension of aqueous protein solutions–Bovine serum albumin. J. Mol. Liq. 2022, 347, 118305. [Google Scholar]
- Lundberg, R.D.; Makowski, H.S. A Comparison of Sulfonate and Carboxylate Ionomers. In Ions in Polymers; Eisenberg, A., Ed.; ACS: Washington, DC, USA, 1980; pp. 21–36. [Google Scholar]
- Minofar, B.; Jungwirth, P.; Das, M.R.; Kunz, W.; Mahiuddin, S. Propensity of formate, acetate, benzoate, and phenolate for the aqueous solution/vapor interface: Surface tension measurements and molecular dynamics simulations. J. Phys. Chem. C 2007, 111, 8242–8247. [Google Scholar] [CrossRef]
- Long, F.A.; Nutting, G.C.; Harkins, W.D. The surface tension of aqueous soap solutions as a function of hydrogen ion (pH) and salt concentration. I. Sodium laurate and sodium nonylate. J. Am. Chem. Soc. 1937, 59, 2197–2203. [Google Scholar] [CrossRef]
- Dobrynin, A.V.; Rubinstein, M. Theory of polyelectrolytes in solutions and at surfaces. Prog. Polym. Sci. 2005, 30, 1049–1118. [Google Scholar] [CrossRef]
- Dobrynin, A.V.; Rubinstein, M.; Obukhov, S.P. Cascade of transitions of polyelectrolytes in poor solvents. Macromolecules 1996, 29, 2974–2979. [Google Scholar] [CrossRef]
- Bai, C.; Herzfeld, J. Surface propensities of the self-ions of water. ACS Cent. Sci. 2016, 2, 225–231. [Google Scholar] [CrossRef]
- Kallay, N.; Preočanin, T.; Selmani, A.; Kovačević, D.; Lützenkirchen, J.; Nakahara, H.; Shibata, O. Thermodynamic model of charging the gas/water interface. J. Phys. Chem. 2015, 119, 997–1007. [Google Scholar] [CrossRef]
- Peng, M.; Duignan, T.T.; Nguyen, C.V.; Nguyen, A.V. From Surface Tension to Molecular Distribution: Modeling Surfactant Adsorption at the Air–Water Interface. Langmuir 2021, 37, 2237–2255. [Google Scholar] [CrossRef]
- Sasaki, T.; Hattori, M.; Sasaki, J.; Nukina, K. Studies of aqueous sodium dodecyl sulfate solutions by activity measurements. Bull. Chem. Soc. Jpn. 1975, 48, 1397–1403. [Google Scholar] [CrossRef] [Green Version]
- Kralchevsky, P.A.; Nagayama, K. Capillary interactions between particles bound to interfaces, liquid films and biomembranes. Adv. Colloid Interface Sci. 2000, 85, 145–192. [Google Scholar] [CrossRef]
- Casson, K.; Johnson, D. Surface-tension-driven flow due to the adsorption and desorption of colloidal particles. J. Colloid Interface Sci. 2001, 242, 279–283. [Google Scholar] [CrossRef]
- Christov, N.C.; Danov, K.D.; Kralchevsky, P.A.; Ananthapadmanabhan, K.P.; Lips, A. Maximum bubble pressure method: Universal surface age and transport mechanisms in surfactant solutions. Langmuir 2006, 22, 7528–7542. [Google Scholar] [CrossRef]
- Ritacco, H.; Langevin, D.; Diamant, H.; Andelman, D. Dynamic surface tension of aqueous solutions of ionic surfactants: Role of electrostatics. Langmuir 2011, 27, 1009–1014. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Gao, Y.; Yang, X. Equilibrium, and dynamic surface properties of sulfosuccinate surfactants. J. Surfactants Deterg. 2014, 17, 1117–1123. [Google Scholar] [CrossRef]














| Polymer | MMA (mol) | MAA (mol) | AIBN (mol) | 1-Dodecanethiol (mol) | THF (mol) |
|---|---|---|---|---|---|
| 1 a | 0.912 | 0.101 | 7.09 × 10−4 | 3.49 × 10−3 | 2.77 |
| 2 a | 0.912 | 0.101 | 7.09 × 10−4 | 1.45 × 10−3 | 2.77 |
| 3 a | 0.912 | 0.101 | 7.09 × 10−4 | 0.76 × 10−3 | 2.77 |
| 4 a | 0.887 | 0.130 | 7.12 × 10−4 | 3.44 × 10−3 | 2.77 |
| 5 a | 0.918 | 0.094 | 7.08 × 10−4 | 1.24 × 10−3 | 2.77 |
| 6 a | 0.941 | 0.067 | 7.06 × 10−4 | 1.6.× 10−3 | 2.77 |
| 7 | 0.953 | 0.053 | 7.04 × 10−4 | 1.6 × 10−3 | 2.77 |
| 8 | 0.852 | 0.170 | 7.16 × 10−4 | 1.6 × 10−3 | 2.77 |
| Sample ID | MW b (g/mol) | PDI c | Monomer Ratio (MMA: MAA) | AN (mg KOH/g) d | Density of Dry CUP, ρp (g/mL) |
|---|---|---|---|---|---|
| Polymer 1 a | 28.9 K | 1.8 | 9:1 | 56.8 | 1.2246 ± 0.0018 |
| Polymer 2 a | 59.8 K | 1.7 | 9:1 | 57.0 | 1.2311 ± 0.0014 |
| Polymer 3 a | 122.5 K | 1.7 | 9:1 | 56.9 | 1.2342 ± 0.0018 |
| Polymer 4 a | 25.4 K | 2.3 | 6.8:1 | 73.2 | 1.2243 ± 0.0018 |
| Polymer 5 a | 73.5 K | 1.7 | 9.8:1 | 52.6 | 1.2315 ± 0.0018 |
| Polymer 6 a | 49.7 K | 1.8 | 14:1 | 37.7 | 1.2307 ± 0.0016 |
| Polymer 7 | 45.4 K | 1.9 | 18:1 | 29.1 | 1.2290 ± 0.0019 |
| Polymer 8 | 50.1 K | 1.6 | 5:1 | 95.8 | 1.2300 ± 0.0012 |
| Sample ID | d(DLS) b (nm) | d(GPC) c (nm) | Charge Density, ρv, (Ions per nm2) |
|---|---|---|---|
| Polymer 1 a | 4.22 | 4.25 | 0.52 |
| Polymer 2 a | 5.38 | 5.40 | 0.66 |
| Polymer 3 a | 6.83 | 6.80 | 0.85 |
| Polymer 4 a | 4.04 | 4.05 | 0.66 |
| Polymer 5 a | 5.76 | 5.80 | 0.66 |
| Polymer 6 a | 5.06 | 5.08 | 0.42 |
| Polymer 7 | 4.90 | 4.92 | 0.32 |
| Polymer 8 | 5.94 | 5.08 d | 1.04 d, 0.83 e |
| Concentration c/c* b, mol/L | Surface Tension a, γ, mN/m | Δγ d | Δγ/Δc (Δγ/Δc*) mN·m2/mol (×103) | |
|---|---|---|---|---|
| Water | 0 | 72.2 | 0.0 | 0 |
| CUPs (Polymer 3) | 0.001/0.0155 b | 68.0 | 4.2 | −4200 (−271) |
| CUPs (Polymer 2) | 0.001/0.0114 b | 70.3 | 1.9 | −1900 (−166) |
| CUPs (Polymer 7) | 0.001/0.0067 b | 71.9 | 0.3 | −300 (−45) |
| QUAT CUPs c | 0.001 | 68.7 | 3.5 | −3500 |
| Sulfonate CUPs c | 0.001 | 65.6 | 6.6 | −6600 |
| SDS c | 0.001 | 65.0 | 7.2 | −7200 |
| Sodium Chloride | 0.35 | 73.9 | −1.7 | 4.86 |
| Sodium Formate c | 1 | 73.2 | −1.0 | 1 |
| Sodium Acetate c | 1 | 70.2 | 2.0 | −2 |
| Sodium Benzoate c | 0.26 | 68.2 | 4.0 | −15.38 |
| Sodium Laurate c | 0.001 | 63.6 | 8.6 | −8600 |
| Sodium Heptanoate | 0.005 | 70.5 | 1.7 | −340 |
| Sodium Octanoate | 0.005 | 65.5 | 6.7 | −1340 |
| Sample ID | Concentration, mol/m3 | γe, mN/m | τ, s | A | R2 |
|---|---|---|---|---|---|
| Polymer 1 | 1.04 | 71.59 | 0.311 | 1.77 | 0.983 |
| 2.10 | 70.77 | 0.401 | 2.57 | 0.993 | |
| 3.53 | 69.81 | 0.426 | 3.69 | 0.994 | |
| Polymer 2 | 0.50 | 71.31 | 0.315 | 1.84 | 0.984 |
| 1.01 | 70.31 | 0.363 | 3.27 | 0.981 | |
| 1.70 | 69.10 | 0.543 | 3.99 | 0.993 | |
| Polymer 3 | 0.24 | 71.25 | 0.264 | 2.64 | 0.995 |
| 0.49 | 69.83 | 0.360 | 4.22 | 0.994 | |
| 1.02 | 68.08 | 0.395 | 5.59 | 0.995 | |
| Polymer 4 | 1.05 | 70.55 | 0.331 | 2.63 | 0.994 |
| 2.39 | 68.05 | 0.374 | 4.22 | 0.997 | |
| 4.03 | 64.99 | 0.406 | 5.59 | 0.995 | |
| Polymer 5 | 0.41 | 71.50 | 0.330 | 2.01 | 0.985 |
| 1.02 | 70.66 | 0.361 | 3.28 | 0.998 | |
| 1.45 | 69.62 | 0.424 | 3.76 | 0.998 |
| Sample ID | Particle Size, nm | Charge Density, Ions/nm2 | Relaxation Time, τ | A | Diffusion Coefficient 10−13 m2/s |
|---|---|---|---|---|---|
| Polymer 1 | 4.22 | 0.52 | 0.311 | 1.77 | 2.49 |
| Polymer 2 | 5.38 | 0.66 | 0.363 | 3.27 | 1.35 |
| Polymer 3 | 6.28 | 0.84 | 0.395 | 5.59 | 0.46 |
| Polymer 4 | 4.04 | 0.66 | 0.331 | 2.63 | 2.30 |
| Polymer 5 | 5.50 | 0.66 | 0.361 | 3.28 | 1.32 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zore, A.; Geng, P.; Van De Mark, M.R. Equilibrium and Dynamic Surface Tension Behavior in Colloidal Unimolecular Polymers (CUP). Polymers 2022, 14, 2302. https://doi.org/10.3390/polym14112302
Zore A, Geng P, Van De Mark MR. Equilibrium and Dynamic Surface Tension Behavior in Colloidal Unimolecular Polymers (CUP). Polymers. 2022; 14(11):2302. https://doi.org/10.3390/polym14112302
Chicago/Turabian StyleZore, Ashish, Peng Geng, and Michael R. Van De Mark. 2022. "Equilibrium and Dynamic Surface Tension Behavior in Colloidal Unimolecular Polymers (CUP)" Polymers 14, no. 11: 2302. https://doi.org/10.3390/polym14112302
APA StyleZore, A., Geng, P., & Van De Mark, M. R. (2022). Equilibrium and Dynamic Surface Tension Behavior in Colloidal Unimolecular Polymers (CUP). Polymers, 14(11), 2302. https://doi.org/10.3390/polym14112302