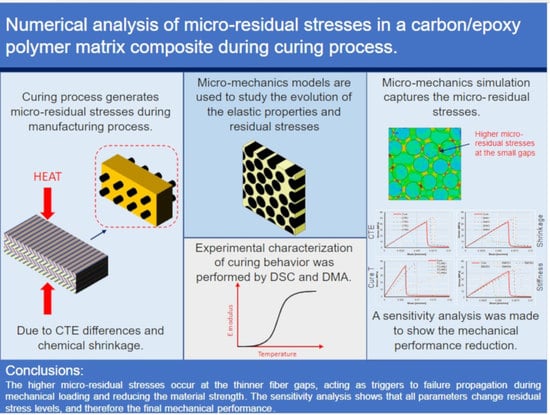
Numerical Analysis of Micro-Residual Stresses in a Carbon/Epoxy Polymer Matrix Composite during Curing Process
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials Selection
2.2. Constitutive Models
2.2.1. Carbon Fibers
2.2.2. Polymer Matrix
- ; : Reaction velocities [1/s].
- ; : Activation energies [J/mol]
- ; Fitting exponents
- : Universal gas constant [8.31432 J/mol.K]
- : Temperature
- Poisson’s ratio at un-cured state
- Poisson’s ratio at cured state
- Elastic modulus at un-cured state
- Elastic modulus at cured state
- Chemical shrinkage at un-cured state
- Chemical shrinkage at cured state.
2.2.3. Thermo-Curing Coupling Strategy
2.3. Finite Element Model
2.4. Micro-Residual Stress Analysis
2.5. Experimental Test Procedures
- Transverse tensile tests following ASTM D3039.
- Longitudinal shear tests following ASTM D3518.
- Transverse shear tests following ASTM D5379.
3. Results and Discussion
3.1. Experimental Results
3.2. Residual Stress Analysis
3.3. Effective Mechanical Properties
3.4. Sensitivity Analysis Results
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Barbero, J.E. Introduction to Composite Materials Design, 3rd ed.; CRC Press: Boca Raton, FL, USA, 2017; ISBN 9781315296494. [Google Scholar]
- Mouritz, A.P. Fibre–Polymer Composites for Aerospace Structures and Engines, 1st ed.; Woodhead Publishing Ltd.: Cambridge, UK, 2012; ISBN 978-1-85573-946-8. [Google Scholar]
- Li, C.; Yin, X.; Liu, Y.; Guo, R.; Xian, G. Long-term service evaluation of a pultruded carbon/glass hybrid rod exposed to elevated temperature, hydraulic pressure and fatigue load coupling. Int. J. Fatigue 2020, 134, 105480. [Google Scholar] [CrossRef]
- Bazli, M.; Abolfazli, M. Mechanical Properties of Fibre Reinforced Polymers under Elevated Temperatures: An Overview. Polymers 2020, 12, 2600. [Google Scholar] [CrossRef] [PubMed]
- Struzziero, G.; Teuwen, J.J.E.; Skordos, A.A. Numerical optimisation of thermoset composites manufacturing processes: A review. Compos. Part A Appl. Sci. Manuf. 2019, 124, 105499. [Google Scholar] [CrossRef]
- D’Mello, R.J.; Maiarù, M.; Waas, A.M. Virtual manufacturing of composite aerostructures. Aeronaut. J. 2016, 120, 61–81. [Google Scholar] [CrossRef] [Green Version]
- Baran, I.; Cinar, K.; Ersoy, N.; Akkerman, R.; Hattel, J.H. A Review on the Mechanical Modeling of Composite Manufacturing Processes. Arch. Comput. Methods Eng. 2017, 24, 365–395. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ersoy, N.; Garstka, T.; Potter, K.; Wisnom, M.R.; Porter, D.; Clegg, M.; Stringer, G. Development of the properties of a carbon fibre reinforced thermosetting composite through cure. Compos. Part A Appl. Sci. Manuf. 2010, 41, 401–409. [Google Scholar] [CrossRef]
- Lavoie, J.A.; Adolfsson, E. Stitch Cracks in Constraint Plies Adjacent to a Cracked Ply. J. Compos. Mater. 2001, 35, 2077–2097. [Google Scholar] [CrossRef]
- Danzi, F.; Fanteria, D.; Panettieri, E.; Mancino, M.C.C. A numerical micro-mechanical study on damage induced by the curing process in carbon/epoxy unidirectional material. Compos. Struct. 2019, 210, 755–766. [Google Scholar] [CrossRef]
- Danzi, F.; Fanteria, D.; Panettieri, E.; Palermo, M. A numerical micro-mechanical study of the influence of fiber–matrix interphase failure on carbon/epoxy material properties. Compos. Struct. 2017, 159, 625–635. [Google Scholar] [CrossRef] [Green Version]
- Kamal, M.R. Thermoset characterization for moldability analysis. Polym. Eng. Sci. 1974, 14, 231–239. [Google Scholar] [CrossRef]
- O’Brien, D.J.; Sottos, N.R.; White, S.R. Cure-dependent Viscoelastic Poisson’s Ratio of Epoxy. Exp. Mech. 2007, 47, 237–249. [Google Scholar] [CrossRef]
- Billotte, C.; Bernard, F.M.; Ruiz, E. Chemical shrinkage and thermomechanical characterization of an epoxy resin during cure by a novel in situ measurement method. Eur. Polym. J. 2013, 49, 3548–3560. [Google Scholar] [CrossRef]
- Nawab, Y.; Casari, P.; Boyard, N.; Jacquemin, F. Characterization of the cure shrinkage, reaction kinetics, bulk modulus and thermal conductivity of thermoset resin from a single experiment. J. Mater. Sci. 2013, 48, 2394–2403. [Google Scholar] [CrossRef] [Green Version]
- Garschke, C.; Parlevliet, P.P.; Weimer, C.; Fox, B.L. Cure kinetics and viscosity modelling of a high-performance epoxy resin film. Polym. Test. 2013, 32, 150–157. [Google Scholar] [CrossRef]
- Chen, D.-L.; Chiu, T.-C.; Chen, T.-C.; Chung, M.-H.; Yang, P.-F.; Lai, Y.-S. Using DMA to Simultaneously Acquire Young’s Relaxation Modulus and Time-dependent Poisson’s Ratio of a Viscoelastic Material. Procedia Eng. 2014, 79, 153–159. [Google Scholar] [CrossRef] [Green Version]
- Péron, M.; Sobotka, V.; Boyard, N.; Le Corre, S. Bulk modulus evolution of thermoset resins during crosslinking: Is a direct and accurate measurement possible? J. Compos. Mater. 2017, 51, 463–477. [Google Scholar] [CrossRef] [Green Version]
- Feng, J.; Guo, Z. Temperature-frequency-dependent mechanical properties model of epoxy resin and its composites. Compos. Part B Eng. 2016, 85, 161–169. [Google Scholar] [CrossRef]
- Shah, D.U.; Schubel, P.J. Evaluation of cure shrinkage measurement techniques for thermosetting resins. Polym. Test. 2010, 29, 629–639. [Google Scholar] [CrossRef] [Green Version]
- Minakuchi, S. In situ characterization of direction-dependent cure-induced shrinkage in thermoset composite laminates with fiber-optic sensors embedded in through-thickness and in-plane directions. J. Compos. Mater. 2015, 49, 1021–1034. [Google Scholar] [CrossRef]
- Seers, B.; Tomlinson, R.; Fairclough, P. Residual stress in fiber reinforced thermosetting composites: A review of measurement techniques. Polym. Compos. 2021, 42, 1631–1647. [Google Scholar] [CrossRef]
- Chevalier, J.; Brassart, L.; Lani, F.; Bailly, C.; Pardoen, T.; Morelle, X.P. Unveiling the nanoscale heterogeneity controlled deformation of thermosets. J. Mech. Phys. Solids 2018, 121, 432–446. [Google Scholar] [CrossRef]
- Yuan, Z.; Wang, Y.; Yang, G.; Tang, A.; Yang, Z.; Li, S.; Li, Y.; Song, D. Evolution of curing residual stresses in composite using multi-scale method. Compos. Part B Eng. 2018, 155, 49–61. [Google Scholar] [CrossRef]
- Yuan, Z.; Zhang, B.; Yang, G.; Yang, Z.; Tang, A.; Li, S.; Li, Y.; Zhao, P.; Wang, Y. Multi-Scale Modeling of Curing Residual Stresses in Composite with Random Fiber Distribution into Consideration. Appl. Compos. Mater. 2019, 26, 983–999. [Google Scholar] [CrossRef]
- Hui, X.; Xu, Y.; Zhang, W. An integrated modeling of the curing process and transverse tensile damage of unidirectional CFRP composites. Compos. Struct. 2021, 263, 113681. [Google Scholar] [CrossRef]
- Melro, A.R.; Camanho, P.P.; Andrade Pires, F.M.; Pinho, S.T. Micromechanical analysis of polymer composites reinforced by unidirectional fibres: Part I—Constitutive modelling. Int. J. Solids Struct. 2013, 50, 1897–1905. [Google Scholar] [CrossRef] [Green Version]
- Melro, A.R.; Camanho, P.P.; Andrade Pires, F.M.; Pinho, S.T. Micromechanical analysis of polymer composites reinforced by unidirectional fibres: Part II—Micromechanical analyses. Int. J. Solids Struct. 2013, 50, 1906–1915. [Google Scholar] [CrossRef] [Green Version]
- Catalanotti, G. On the generation of RVE-based models of composites reinforced with long fibres or spherical particles. Compos. Struct. 2016, 138, 84–95. [Google Scholar] [CrossRef] [Green Version]
- Barbero, E.J. Finite Element Analysis of Composite Materials Using AbaqusTM.; CRC Press: Boca Raton, FL, USA, 2013; ISBN 9781466516632. [Google Scholar]
- Yvonnet, J.; Auffray, N.; Monchiet, V. Computational second-order homogenization of materials with effective anisotropic strain-gradient behavior. Int. J. Solids Struct. 2020, 191–192, 434–448. [Google Scholar] [CrossRef]
- Coenen, E.W.C.; Kouznetsova, V.G.; Geers, M.G.D. Novel boundary conditions for strain localization analyses in microstructural volume elements. Int. J. Numer. Methods Eng. 2012, 90, 1–21. [Google Scholar] [CrossRef]
- Otero, F.; Oller, S.; Martinez, X. Multiscale Computational Homogenization: Review and Proposal of a New Enhanced-First-Order Method. Arch. Comput. Methods Eng. 2018, 25, 479–505. [Google Scholar] [CrossRef] [Green Version]
- Otero, F.; Oller, S.; Martinez, X.; Salomón, O. Numerical homogenization for composite materials analysis. Comparison with other micro mechanical formulations. Compos. Struct. 2015, 122, 405–416. [Google Scholar] [CrossRef] [Green Version]
- Toray Composite Materials America, Inc. T700 Technical Data Sheet. 2018. Available online: https://www.toraycma.com/resources/data-sheets/ (accessed on 2 June 2021).
- Soden, P. Lamina properties, lay-up configurations and loading conditions for a range of fibre-reinforced composite laminates. Compos. Sci. Technol. 1998, 58, 1011–1022. [Google Scholar] [CrossRef]
- Bai, X.; Bessa, M.A.; Melro, A.R.; Camanho, P.P.; Guo, L.; Liu, W.K. High-fidelity micro-scale modeling of the thermo-visco-plastic behavior of carbon fiber polymer matrix composites. Compos. Struct. 2015, 134, 132–141. [Google Scholar] [CrossRef] [Green Version]
- Murakami, S. Continuum Damage Mechanics; Solid Mechanics and Its Applications; Springer: Dordrecht, The Netherlands, 2012; Volume 185, ISBN 978-94-007-2665-9. [Google Scholar]
- de Souza Neto, E.A.; Peri, D.; Owen, D.R.J. Computational Methods for Plasticity; John Wiley & Sons, Ltd.: Chichester, UK, 2008; ISBN 9780470694626. [Google Scholar]
- Dai, J.; Xi, S.; Li, D. Numerical Analysis of Curing Residual Stress and Deformation in Thermosetting Composite Laminates with Comparison between Different Constitutive Models. Materials 2019, 12, 572. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Melro, A.R.; Camanho, P.P.; Pinho, S.T. Influence of geometrical parameters on the elastic response of unidirectional composite materials. Compos. Struct. 2012, 94, 3223–3231. [Google Scholar] [CrossRef]
- Tan, W.; Martínez-Pañeda, E. Phase field predictions of microscopic fracture and R-curve behaviour of fibre-reinforced composites. Compos. Sci. Technol. 2021, 202, 108539. [Google Scholar] [CrossRef]


















| Properties | Value |
|---|---|
| Fiber diameter (mm) | 7 × 10−3 |
| Density (kg/m3) | 1800 |
| Specific Heat (kJ/kg·K) | 0.752 |
| Thermal Conductivity (W/m·K) | 9.38 |
| (°C−1) | −0.38 × 10−6 |
| (°C−1) | 6.94 × 10−6 |
| (GPa) | 230 |
| (GPa) | 15 |
| (n.d) | 0.2 |
| (GPa) | 15 |
| (GPa) | 7 |
| Properties | Value |
|---|---|
| Density (kg/m3) | 1310 |
| Specific Heat (kJ/kg·K) | 0.679 |
| Thermal Cond. (W/m·K) | 0.15 1 |
| (10−6 °C−1) | 61.0 1 |
| Shrinkage (%) | 2.0 1 |
| (°C) | 135 2 |
| (MPa) | 2850 |
| (n.d) | 0.33 |
| (n.d) | 0.30 1 |
| (MPa) | 55 |
| (MPa) | 81 3 |
| (MPa) | 65 |
| (MPa) | 93 3 |
| (%) | 2.6 |
| (N/mm) | 0.12 3 |
| Test | Description | Elastic Tensor Parameters | Yield Surface Parameters | Failure Surface Parameters |
|---|---|---|---|---|
| Longitudinal uniaxial tension |  | ; | - | - |
| Transverse uniaxial tension 1 |  | |||
| Transverse shear |  | |||
| Longitudinal shear |  |
| Time (min) | 0 | 23.25 | 38.25 | 50 | 110 | 130 |
| Temperature (°C) | 25 | 85 | 85 | 120 | 120 | 20 |
| Parameter | Value | ||||
|---|---|---|---|---|---|
| Nominal | Case 1 | Case 2 | Case 3 | Case 4 | |
| Shrinkage (mm/mm) | −0.02 | −0.01 | −0.015 | −0.025 | −0.03 |
| CTE (10−6 °C−1) | 60 | 20 | 40 | 80 | 100 |
| Elastic mod. (MPa) | 2280 | 2565 | 2850 | 3135 | 3420 |
| T cure (°C) | 120 | 90 | 105 | 130 | - |
| 3.24 × 1015 | 134,627 | 0 | 0 | 1.00 | 0 |
| Test Standard | Property | Average | Standard Deviation |
|---|---|---|---|
| ASTM D3039 | (MPa) | 7313 | 192 |
| ASTM D3039 | (n/d) | 0.0109 | 0.0044 |
| ASTM D5379 | (MPa) | 2812.8 | 73.9 |
| ASTM D3518 | (MPa) | 3215 | 187 |
| ASTM D3039 | (MPa) | 42.91 | 4.15 |
| ASTM D5379 | (MPa) | 22.34 | 2.17 |
| ASTM D3518 | (MPa) | 21.41 | 1.577 |
| Experimental Results | Numerical Predictions | Experiments vs. Cure Predictions (%) | ||
|---|---|---|---|---|
| Cure | No-Cure | |||
| (MPa) | 7313 ± 192 | 7151 ± 114 | 7235 ± 55 | 2.3 |
| (n/d) | 0.0109 ± 0.0044 | 0.0115 ± 0.0002 | 0.0115 ± 0.0002 | −5.1 |
| (n/d) | 0.34 1 | 0.34 ± 0.01 | 0.34 ± 0.01 | −0.6 |
| (MPa) | 2729 ± 132 | 2674 ± 71 | 2733 ± 74 | 2.0 |
| (MPa) | 3215 ± 187 | 3353 ± 63 | 3460 ± 80 | −4.3 |
| (MPa) | 42.9 ± 4.2 | 46.0 ± 2.0 | 51.9 ± 1.8 | −7.3 |
| (MPa) | 22.3 ± 2.2 | 25.0 ± 2.6 | 32.3 ± 0.7 | −12.2 |
| (MPa) | 21.4 ± 1.6 | 23.5 ± 1.2 | 26.8 ± 0.8 | −9.6 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gonçalves, P.T.; Arteiro, A.; Rocha, N.; Pina, L. Numerical Analysis of Micro-Residual Stresses in a Carbon/Epoxy Polymer Matrix Composite during Curing Process. Polymers 2022, 14, 2653. https://doi.org/10.3390/polym14132653
Gonçalves PT, Arteiro A, Rocha N, Pina L. Numerical Analysis of Micro-Residual Stresses in a Carbon/Epoxy Polymer Matrix Composite during Curing Process. Polymers. 2022; 14(13):2653. https://doi.org/10.3390/polym14132653
Chicago/Turabian StyleGonçalves, Paulo Teixeira, Albertino Arteiro, Nuno Rocha, and Luis Pina. 2022. "Numerical Analysis of Micro-Residual Stresses in a Carbon/Epoxy Polymer Matrix Composite during Curing Process" Polymers 14, no. 13: 2653. https://doi.org/10.3390/polym14132653
APA StyleGonçalves, P. T., Arteiro, A., Rocha, N., & Pina, L. (2022). Numerical Analysis of Micro-Residual Stresses in a Carbon/Epoxy Polymer Matrix Composite during Curing Process. Polymers, 14(13), 2653. https://doi.org/10.3390/polym14132653