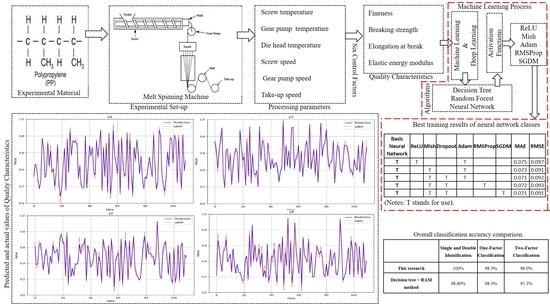
Quality Prediction and Abnormal Processing Parameter Identification in Polypropylene Fiber Melt Spinning Using Artificial Intelligence Machine Learning and Deep Learning Algorithms
Abstract
:1. Introduction
2. Methods and Materials
2.1. Random Forest
- (1)
- Define a random sample of size n, and randomly select n data from the data set.
- (2)
- From the selected n data, a decision tree is trained, d features are randomly extracted for each node in the decision tree, and then the features are used to divide the node.
- (3)
- Repeat steps 1~2 k times with improvements. The more commonly used improvement is Adaboost.
- (4)
- Summarize the predictions of all decision trees and decide the result of this classification by voting majority or weighted voting.
2.2. Neural Network
2.3. Activation Functions
2.4. Optimization Techniques
2.5. Materials
3. Experiment Plan
3.1. Materials Analysis
3.2. Multi-Quality Characteristic Prediction
3.2.1. Experimental Data
3.2.2. Data Processing
3.2.3. Neural Network Training
3.2.4. Evaluation Criteria and Training Results
3.3. Creating Historical Data and Abnormal Samples
3.4. Abnormal Processing Parameter Classifier Model Training
3.4.1. Single and Double Identification
3.4.2. One-Factor Classification
3.4.3. Two-Factor Classification
4. Conclusions
- (1)
- The deep learning neural network is used for experiments, 440 pieces of historical data are trained, and multiple quality optimization parameters are searched by using the characteristic grid of deep learning rapid calculation. The deep learning neural network was used to generate quality predictions, trained on a 440-item historical data set, and multiple quality optimization parameters were searched for using rapid deep-learning characteristic grid calculations. Compared with the traditional Taguchi analysis method, the neural network model conducts self-training and learning using past historical data, which means the research can proceed faster, analysis is more efficient, and conclusions are more robust, because a calculation error in one step will not affect the overall detection system.
- (2)
- This research compared several artificial intelligence machines learning and deep learning classifiers that have obtained outstanding results in the related literature, and finally selected the random forest as being the best, because its classifier belongs to ensemble learning, and the classifier is resistant to overfitting. Its ability to detect the cause of quality problems was better than that of other classifiers. As an indication the success rate of single and double identification was 100%, the success rate of single factor classification was 98.3%, and the success rate of double factor classification was 96.0%. It can be seen that the proposed method offers an effective way to identify the problematic machine settings, causing problems in quality control after the engineer has measurements of the abnormality so that the settings can be quickly modified to improve production yield.
- (3)
- This study applied the methods of artificial intelligence to the development of an abnormal processing PP fiber melt spinning parameter identification system which can quickly find abnormal settings and reduce unnecessary cost and waste. In the future, different online detection systems matching the capabilities of this system for various other kinds of material will be added to the resources available to production engineers seeking to apply the developed identification system for its functions of selection and evaluation.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Kuo, C.F.J.; Syu, S.S.; Lin, C.H.; Peng, K.C. The application of principal component analysis and gray relational method in the optimization of the melt spinning process using the cooling air system. Text Res. J. 2013, 83, 371–380. [Google Scholar] [CrossRef]
- Asmatulu, R.; Khan, W.S. Synthesis and Applications of Electrospun Nanofibers, Micro and Nano Technologies; Elsevier Publishing: Amsterdam, The Netherlands, 2019; pp. 1–15. [Google Scholar]
- Iba, H.; Nasimul, N. Deep Neural Evolution; Springer: Berlin/Heidelberg, Germany, 2020. [Google Scholar]
- Lam, Y.C.; Zhai, L.Y.; Tai, K.; Fok, S.C. An evolutionary approach for cooling system optimization in plastic injection moulding. Int. J. Prod. Res. 2004, 42, 2047–2061. [Google Scholar] [CrossRef]
- Chen, W.C.; Wang, M.W.; Fu, G.L.; Chen, C.T. Optimization of plastic injection molding process via Taguchi’s parameter design method, BPNN, and DFP. In Proceedings of the 2008 International Conference on Machine Learning and Cybernetics, IEEE, Kumming, China, 12–15 July 2008; Volume 6, pp. 3315–3321. [Google Scholar]
- Abiodun, O.I.; Jantan, A.; Omolara, A.E.; Dada, K.V.; Mohamed, N.A.; Arshad, H. State-of-the-art in artificial neural network applications: A survey. Heliyon 2018, 4, e00938. [Google Scholar] [CrossRef] [Green Version]
- Majumdar, P.K.; Majumdar, A. Predicting the breaking elongation of ring spun cotton yarns using mathematical, statistical, and artificial neural network models. Text. Res. J. 2004, 74, 652–655. [Google Scholar] [CrossRef]
- Dave, V.S.; Dutta, K. Neural network-based models for software effort estimation: A review. Artif. Intell. Rev. 2014, 42, 295–307. [Google Scholar] [CrossRef]
- Bai, Y.; Li, C.; Sun, Z.; Chen, H. Deep neural network for manufacturing quality prediction. In Proceedings of the 8th IEEE Prognostics and System Health Management Conference, Harbin, China, 9–12 July 2017. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef] [Green Version]
- Sugumaran, V.; Ramachandran, K.I. Automatic rule learning using decision tree for fuzzy classifier in fault diagnosis of roller bearing. Mech. Syst. Signal Processing 2007, 21, 2237–2247. [Google Scholar] [CrossRef]
- Wang, Q.; Ahmad, W.; Ahmad, A.; Aslam, F.; Mohamed, A.; Vatin, N.I. Application of Soft Computing Techniques to Predict the Strength of Geopolymer Composites. Polymers 2022, 14, 1074. [Google Scholar] [CrossRef]
- Nafees, A.; Amin, M.N.; Khan, K.; Nazir, K.; Ali, M.; Javed, M.F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Modeling of mechanical properties of silica fume-based green concrete using machine learning techniques. Polymers 2021, 14, 30. [Google Scholar] [CrossRef]
- Zimmerman, R.K.; Balasubramani, G.K.; Nowalk, M.P.; Eng, H.; Urbanski, L.; Jackson, M.L.; Jackson, L.A.; McLean, H.Q.; Belongia, E.A.; Monto, A.S.; et al. Classification and regression tree (CART) analysis to predict influenza in primary care patients. BMC Infect. Dis. 2016, 16, 503. [Google Scholar] [CrossRef] [Green Version]
- Nafees, A.; Javed, M.F.; Khan, S.; Nazir, K.; Farooq, F.; Aslam, F.; Musarat, M.A.; Vatin, N.I. Predictive Modeling of Mechanical Properties of Silica Fume-Based Green Concrete Using Artificial Intelligence Approaches: MLPNN, ANFIS, and GEP. Materials 2021, 14, 7531. [Google Scholar] [CrossRef] [PubMed]
- Cerrada, M.; Zurita, G.; Cabrera, D.; Sánchez, R.V.; Artés, M.; Li, C. Fault diagnosis in spur gears based on genetic algorithm and random forest. Mech. Syst. Signal Process. 2016, 70, 87–103. [Google Scholar] [CrossRef]
- Li, C.; Sanchez, R.; Zurita, G.; Cerrada, M.; Cabrera, D.; Vásquez, R.E. Gearbox fault diagnosis based on deep random forest fusion of acoustic and vibratory signals. Mech. Syst. Signal Process. 2016, 76, 283–293. [Google Scholar] [CrossRef]
- Esmaily, H.; Tayefi, M.; Doosti, H.; Ghayour-Mobarhan, M.; Nezami, H.; Amirabadizadeh, A. A comparison between decision tree and random forest in determining the risk factors associated with type 2 diabetes. J. Res. Health Sci. 2018, 18, 412. [Google Scholar]
- Yanjun, Q. Random forest for bioinformatics. In Ensemble Machine Learning; Springer: Boston, MA, USA, 2012; pp. 307–323. [Google Scholar]
- Ansoategui, F.J.; Campa, C.; Díez, M. Influence of the machine tool compliance on the dynamic performance of the servo drives. Int. J. Adv. Manuf. Technol. 2017, 90, 2849–2861. [Google Scholar] [CrossRef]
- Ali, J.B.; Fnaiech, N.L.; Chebel-Morello, S.B.; Fnaiech, F. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals. Appl. Acoust. 2015, 89, 16–27. [Google Scholar]
- Hastie, T.R.; Friedman, T.J. Random forests. In The Elements of Statistical Learning; Springer: New York, NY, USA, 2019; pp. 587–604. [Google Scholar]
- Dietterich, T.G. Ensemble learning. Handb. Brain Theory Neural Netw. 2002, 2, 110–125. [Google Scholar]
- Ying, C.; Qi-Guang, M.; Jia-Chen, L.; Lin, G. Advance and prospects of AdaBoost algorithm. Acta Autom. Sin. 2013, 39, 745–758. [Google Scholar]
- Nwankpa, C.; Ijomah, W.; Gachagan, A.; Marshall, S. Activation functions: Comparison of trends in practice and research for deep learning. arXiv 2018, arXiv:1811.03378. [Google Scholar]
- Ruder, S. An overview of gradient descent optimization algorithms. arXiv 2016, arXiv:1609.04747. [Google Scholar]
- Elmaaty, T.A.; Taweel, F.E.I.; Elsisi, H.; Okubayashi, S. Water free dyeing of polypropylene fabric under supercritical carbon dioxide and comparison with its aqueous analogue. J. Supercrit. Fluids 2018, 139, 114–121. [Google Scholar] [CrossRef]
- Elmaaty, T.A.; Sofan, M.; Elsisi, H.; Kosbar, T.; Negm, E.; Hirogaki, K.; Tabata, I.; Hori, T. Optimization of an eco-friendly dyeing process in both laboratory scale and pilot scale supercritical carbon dioxide unit for polypropylene fabrics with special new disperse dyes. J. CO2 Util. 2019, 33, 365–371. [Google Scholar] [CrossRef]
- Gonzalez, T.F. Handbook of Approximation Algorithms and Metaheuristics; Chapman and Hall/CRC: Boca Raton, FL, USA, 2007. [Google Scholar]
- Misra, D. Mish: A self-regularized non-monotonic activation function. arXiv 2019, arXiv:1908.08681. [Google Scholar]
- Barry, P. Sigmoid functions and exponential Riordan arrays. arXiv 2017, arXiv:1702.04778. [Google Scholar]
- Bergstra, J.; Bengio, Y. Random search for hyper-parameter optimization. J. Mach. Learn. Res. 2012, 13, 281–305. [Google Scholar]
- Schaul, T.; Antonoglou, I.; Silver, D. Unit tests for stochastic optimization. arXiv 2013, arXiv:1312.6055. [Google Scholar]
- Wang, Y.; Liu, J.; Mišić, J.; Mišić, V.B.; Lv, S.; Chang, X. Assessing optimizer impact on dnn model sensitivity to adversarial examples. IEEE Access 2019, 7, 152766–152776. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Saraswat, S.; Yadava, G.S. An overview on reliability, availability, maintainability and supportability (RAMS) engineering. Int. J. Qual. Reliab. Manag. 2008, 25, 330–344. [Google Scholar] [CrossRef]
- Kuo, C.F.J.; Huang, C.C.; Yang, C.H. Integration of multivariate control charts and decision tree classifier to determine the faults of the quality characteristic(s) of a melt spinning machine used in polypropylene as-spun fiber manufacturing Part I: The application of the Taguchi method and principal component analysis in the processing parameter optimization of the melt spinning process. Text. Res. J. 2021, 91, 1815–1829. [Google Scholar]



















| Range | Screw Temperature | Gear Pump Temperature | Die Head Temperature | Screw Speed | Gear Pump Speed | Take-Up Speed |
|---|---|---|---|---|---|---|
| Lowest | 160 °C | 200 °C | 210 °C | 5 rpm | 15 rpm | 300 rpm |
| Highest | 200 °C | 240 °C | 250 °C | 10 rpm | 25 rpm | 700 rpm |
| Neurons in Each Layer | 20 | 30 | 40 | 50 | |
|---|---|---|---|---|---|
| No. of Hidden Layers | |||||
| 2 | 0.084 | 0.079 | 0.088 | 0.085 | |
| 3 | 0.078 | 0.078 | 0.079 | 0.080 | |
| 4 | 0.076 | 0.074 | 0.073 | 0.074 | |
| 5 | 0.075 | 0.075 | 0.075 | 0.077 | |
| Neurons in Each Layer | 20 | 30 | 40 | 50 | |
|---|---|---|---|---|---|
| No. of Hidden Layers | |||||
| 2 | 0.104 | 0.102 | 0.105 | 0.104 | |
| 3 | 0.101 | 0.101 | 0.102 | 0.102 | |
| 4 | 0.098 | 0.095 | 0.093 | 0.096 | |
| 5 | 0.097 | 0.097 | 0.098 | 0.101 | |
| Basic Neural Network | ReLU | Mish | Dropout | Adam | RMSProp | SGDM | MAE | RMSE |
|---|---|---|---|---|---|---|---|---|
| T | T | T | 0.075 | 0.097 | ||||
| T | T | T | 0.073 | 0.091 | ||||
| T | T | T | T | 0.071 | 0.092 | |||
| T | T | T | T | 0.072 | 0.093 | |||
| T | T | T | T | 0.071 | 0.091 |
| Quality | Fineness | Breaking Strength | Elongation at Break | Modulus of Resilience | |
|---|---|---|---|---|---|
| No. | |||||
| 1 | 0.3756 | 0.4750 | 0.7792 | 0.3485 | |
| 2 | 0.4911 | 0.6983 | 0.1402 | 0.9094 | |
| 3 | 0.6038 | 0.1909 | 0.6664 | 0.8443 | |
| 4 | 0.7908 | 0.1200 | 1 | 0.7692 | |
| 5 | 0.1688 | 0.3887 | 0 | 0.5886 | |
| 6 | 0.7128 | 1 | 0.2288 | 0.1552 | |
| 7 | 0.6479 | 0.5397 | 0.0466 | 0.7645 | |
| 8 | 0.4227 | 0 | 0.7121 | 0.5876 | |
| 9 | 0.5020 | 0.6814 | 0.5338 | 0.6714 | |
| 10 | 0.1160 | 0.4072 | 0.6850 | 1 | |
| 11 | 0.4236 | 0.5923 | 0.7031 | 0 | |
| 12 | 0.9014 | 0.5112 | 0.4281 | 0.9307 | |
| 13 | 0.1014 | 0.8892 | 0.8902 | 0.9345 | |
| 14 | 0.7915 | 0.7402 | 0.6798 | 0.4314 | |
| 15 | 0 | 0.2648 | 0.1486 | 0.4834 | |
| 16 | 0.4965 | 0.3988 | 0.7897 | 0.6255 | |
| 17 | 1 | 0.6118 | 0.5782 | 0.6722 | |
| 18 | 0.1556 | 0.5548 | 0.5080 | 0.5609 | |
| 19 | 0.1875 | 0.9408 | 0.7626 | 0.8439 | |
| 20 | 0.0891 | 0.8904 | 0.8377 | 0.9105 | |
| Fineness (dB) | Breaking Strength (dB) | Elongation at Break (dB) | Modulus of Resilience (dB) | |
|---|---|---|---|---|
| Predication value | 0.183 | 0.872 | 0.947 | 0.935 |
| Denormalized value | 243 | 3.4 | 643 | 9.13 |
| Best Parameter Data | |||||
|---|---|---|---|---|---|
| Quality | Fineness (Diner) | Breaking Strength (N/mm2) | Elongation at Break (%) | Modulus of Resilience (N/mm2) | |
| Samples | |||||
| 1 | 236 | 3.1 | 641.972 | 9.03 | |
| 2 | 237 | 2.8 | 648.305 | 9.40 | |
| 3 | 237 | 3.4 | 648.357 | 9.39 | |
| 4 | 231 | 2.8 | 644.224 | 9.28 | |
| 5 | 241 | 3 | 648.265 | 9.45 | |
| 6 | 249 | 3.6 | 635.923 | 9.52 | |
| 7 | 227 | 2.9 | 642.845 | 8.74 | |
| 8 | 231 | 3.6 | 641.218 | 8.82 | |
| 9 | 232 | 3.6 | 646.801 | 9.30 | |
| 10 | 238 | 3.5 | 645.216 | 9.36 | |
| 11 | 241 | 3.5 | 643.506 | 9.03 | |
| 12 | 231 | 3.5 | 640.725 | 9.48 | |
| 13 | 236 | 3 | 641.378 | 9.03 | |
| 14 | 247 | 3.4 | 646.776 | 9.49 | |
| 15 | 251 | 2.8 | 643.393 | 9.79 | |
| 16 | 245 | 3.5 | 642.942 | 8.99 | |
| 17 | 240 | 2.7 | 641.155 | 9.54 | |
| 18 | 240 | 3.6 | 642.811 | 9.20 | |
| 19 | 234 | 3.6 | 640.911 | 9.04 | |
| 20 | 257 | 3.6 | 646.926 | 8.87 | |
| A | B | C | D | E | F | |
|---|---|---|---|---|---|---|
| Screw Temperature (°C) | Gear Pump Temperature (°C) | Die Head Temperature (°C) | Screw Speed (rpm) | Gear Pump Speed (rpm) | Take-Up Speed (rpm) | |
| Normal | 180 | 220 | 240 | 7.5 | 15 | 700 |
| Abnormal 1 | 190 | 200 | 220 | 5 | 20 | 300 |
| Abnormal 2 | 200 | 210 | 230 | 10 | 25 | 500 |
| Quality | Fineness (dB) | Breaking Strength (dB) | Elongation at Break (dB) | Modulus of Resilience (dB) | |
|---|---|---|---|---|---|
| Sets | |||||
| 1 | 224 | 2 | 643.791 | 8.97 | |
| 2 | 249 | 2.8 | 655.667 | 7.66 | |
| 3 | 562 | 1.8 | 591.197 | 9.14 | |
| 4 | 598 | 2.9 | 642.068 | 6.99 | |
| 5 | 316 | 2.2 | 520.831 | 8.92 | |
| 6 | 283 | 3.3 | 531.791 | 6.09 | |
| 7 | 551 | 2.8 | 645.044 | 8.73 | |
| 8 | 347 | 3.1 | 647.541 | 8.96 | |
| 9 | 254 | 3.2 | 606.269 | 9.60 | |
| 10 | 296 | 2.2 | 638.988 | 8.93 | |
| Processing Parameter | Screw Temperature | Gear Pump Temperature | Die Head Temperature | Screw Speed | Gear Pump Speed | Take-Up Speed | |
|---|---|---|---|---|---|---|---|
| Sets | |||||||
| 1 | 0 | 1 | 0 | 0 | 0 | 0 | |
| 2 | 1 | 0 | 0 | 1 | 0 | 0 | |
| 3 | 0 | 0 | 0 | 1 | 1 | 0 | |
| 4 | 0 | 0 | 0 | 0 | 0 | 1 | |
| 5 | 0 | 1 | 0 | 0 | 1 | 0 | |
| 6 | 1 | 0 | 0 | 0 | 0 | 1 | |
| 7 | 0 | 0 | 1 | 0 | 0 | 0 | |
| 8 | 0 | 0 | 0 | 1 | 0 | 0 | |
| 9 | 1 | 0 | 0 | 0 | 0 | 0 | |
| 10 | 0 | 1 | 1 | 0 | 0 | 0 | |
| Method | Single and Double Identification Detection Success Rate |
|---|---|
| Decision tree | 98.5% |
| Radom forest | 100% |
| Support vector machine | 98.1% |
| Neural network | 98.1% |
| Method | Single Factor Classification Detection Success Rate |
|---|---|
| Decision tree | 95.0 % |
| Radom forest | 98.3 % |
| Neural network | 96.8 % |
| Method | Two-Factor Classification Detection Success Rate |
|---|---|
| Decision tree | 91.8% |
| Radom forest | 96.0% |
| Neural network | 89.3% |
| Single and Double Identification | One-Factor Classification | Two-Factor Classification | ||
|---|---|---|---|---|
| This research | 100% | 98.3% | 96.0% | |
| Decision tree + RAM method | 98.60% | 98.3% | 95.3% | |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gope, A.K.; Liao, Y.-S.; Kuo, C.-F.J. Quality Prediction and Abnormal Processing Parameter Identification in Polypropylene Fiber Melt Spinning Using Artificial Intelligence Machine Learning and Deep Learning Algorithms. Polymers 2022, 14, 2739. https://doi.org/10.3390/polym14132739
Gope AK, Liao Y-S, Kuo C-FJ. Quality Prediction and Abnormal Processing Parameter Identification in Polypropylene Fiber Melt Spinning Using Artificial Intelligence Machine Learning and Deep Learning Algorithms. Polymers. 2022; 14(13):2739. https://doi.org/10.3390/polym14132739
Chicago/Turabian StyleGope, Amit Kumar, Yu-Shu Liao, and Chung-Feng Jeffrey Kuo. 2022. "Quality Prediction and Abnormal Processing Parameter Identification in Polypropylene Fiber Melt Spinning Using Artificial Intelligence Machine Learning and Deep Learning Algorithms" Polymers 14, no. 13: 2739. https://doi.org/10.3390/polym14132739
APA StyleGope, A. K., Liao, Y.-S., & Kuo, C.-F. J. (2022). Quality Prediction and Abnormal Processing Parameter Identification in Polypropylene Fiber Melt Spinning Using Artificial Intelligence Machine Learning and Deep Learning Algorithms. Polymers, 14(13), 2739. https://doi.org/10.3390/polym14132739