Squeezing Mechanical Analysis and Model Establishment of the Viscoelastic Rubber-Strip-Feeding Process of the Cold-Feed Rubber Extruder
Abstract
:1. Introduction
2. Physical Model and Squeezing Velocity
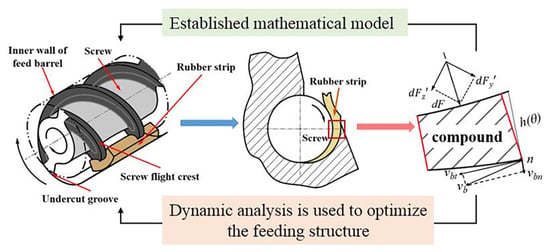
2.1. Physical Model
2.2. Squeezing Velocity
3. Mathematical Model
3.1. Kinematic Exchange
3.2. Velocity and Pressure Distributions
3.3. Total Squeezing Force
3.4. Power Consumption
4. Materials and Methods
4.1. Experiment and Materials
4.2. Measurements of Viscosity and the Sliding Friction Coefficient
- (1)
- Viscosity
- (2)
- Sliding friction coefficient
5. Results and Discussion
- (1)
- Pressure distribution
- (2)
- Power consumption
6. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Schöppner, V.; Schadomsky, M.; Hopmann, C.; Lemke, F. Investigations of the mixing behaviour of pin-type rubber extruders. AIP Conf. Proc. 2016, 1713, 130003-1–130003-5. [Google Scholar] [CrossRef]
- Lewandowski, A.; Wilczyński, K. Modeling of Twin Screw Extrusion of Polymeric Materials. Polymers 2022, 2, 274. [Google Scholar] [CrossRef] [PubMed]
- Francis, P.J.J.; Joseph, R.; George, K.E. Significance of Feeding Rate in the Extrusion of Filled and Gum IIR Vulcanizates. Int. J. Polym. Mater. Polym. Biomater. 1997, 38, 65–78. [Google Scholar] [CrossRef]
- Water, H. Schiesser and Zürich, Apparatus for Automatic Uniform Drawing-in of Elastomeric Material into Worm Extruders. U.S. Patent 4,286,882, 1 September 1981. [Google Scholar]
- Yanchang, L.; Fang, Y.; Chong, M.; Zhenglin, H.; Guangyi, L. Feeding Behaviour of Cold-Feed Rubber Extruders. Polym. Mater. Sci. Eng. 2020, 36, 103–108. [Google Scholar]
- Jianbin, L.; Liangwei, F.; Jinbo, Z.; Shejun, D. Study on the Conveying Capacity of Feed Section of Rubber Cold Feeding extruder. Rubber/Plast. Technol. Equip. 1984, 4, 13–21. [Google Scholar]
- Limper, A.; Schramm, D. Process Description for the Extrusion of Rubber Compounds-Development and Evaluation of a Screw Design Software. Macromol. Mater. Eng. 2002, 287, 824–835. [Google Scholar] [CrossRef]
- Alan, N. Gent, Engineering with Rubber, 3rd ed.; Hanser Publishers: Munich, Germany, 2012; p. 18. [Google Scholar] [CrossRef]
- Raymond, L.C. Extruder for Elastomeric Material. U.S. Patent 4,718,770, 12 January 1988. [Google Scholar]
- Gerd, C.L. Method of Maintaining the Force of a Stripper Blade on an Extruder Feed Roller Constant and an Apparatus therefor. U.S. Patent 5,068,069, 26 November 1991. [Google Scholar]
- Baiyuan, L.; Yanchang, L.; Penzhen, L.; Dianrui, Z. Study on the influence of feeding method on extrusion process of rubber cold feeding extruder. Rubber Technol. Equip. 1999, 25, 1–6. [Google Scholar]
- John, L.R. Leakage-free Feed Roll Assembly for an Extruder Machine. U.S. Patent 7, 160, 099B2, 7 February 2007. [Google Scholar]
- Thomas, J.O. Extruder Feed Section with Pivotable Feed Roll Assembly. U.S. Patent 8, 496, 463B2, 30 July 2013. [Google Scholar]
- Brand, W. Apparatus to Control Feed of Material to an Extruder. U.S. Patent 3,785,527, 15 January 1974. [Google Scholar]
- Ernest, S. Ulm, Feed Control Mechanism. U.S. Patent 3,858,857, 7 January 1975. [Google Scholar]
- Anders, D. Method of and Apparatus for the Controlled Feeding of Quantity of Material into the Intake Opeening of an Extruder for Processing Rubber or Plastics Material. U.S. Patent 4,247,272, 27 October 1981. [Google Scholar]
- Winther, G.; Almdal, K.; Kramer, O. Determination of polymer melt viscosity by squeezing flow with constant plate velocity. J. Non-Newtonian Fluid Mech. 1991, 39, 119–136. [Google Scholar] [CrossRef]
- Tashtoush, B.; Tahat, M.; Probert, D. Heat transfers and radial flows via a visous fluid squeezed between two parallel disks. Appl. Energy 2001, 68, 275–288. [Google Scholar] [CrossRef]
- Debbaut, B. Non-isothermal and viscoelastic effects in the squeeze flow between infinite plates. J. Non-Newton. Fluid Mech. 2001, 98, 15–31. [Google Scholar] [CrossRef]
- Phan-Thien, N.; Tanner, R. Lubrication squeeze-film theory for the oldroyd-b fluid. J. Non-Newton. Fluid Mech. 1984, 14, 327–335. [Google Scholar] [CrossRef]
- Phan-Thien, N.; Dudek, J.; Boger, D.; Tirtaatmadja, V. Squeeze film flow of ideal elastic liquids. J. Non-Newton. Fluid Mech. 1985, 18, 227–254. [Google Scholar] [CrossRef]
- Gartling, D.K.; Phan-Thien, N. A numerical simulation of a plastic fluid in a parallel-plate plastometer. J. Non-Newton. Fluid Mech. 1984, 14, 347–360. [Google Scholar] [CrossRef]
- Phan-Thien, N.; Sugeng, F.; Tanner, R. The squeeze-film flow of a viscoelastic fluid. J. Non-Newt. Fluid Mech. 1987, 24, 97–119. [Google Scholar] [CrossRef]
- Lee, S.; Denn, M.; Crochet, M.; Metzner, A.; Riggins, G. Compressive flow between parallel disks: II. oscillatory behavior of viscoelastic materials under a constant load. J. Non-Newton. Fluid Mech. 1984, 14, 301–325. [Google Scholar] [CrossRef]
- Lipscomb, G.; Denn, M. Flow of bingham fluids in complex geometries. J. Non-Newton. Fluid Mech. 1984, 14, 337–346. [Google Scholar] [CrossRef]
- Kompani, M.; Venerus, D.C. Equibiaxial extensional flow of polymer melts via lubricated squeezing flow. I. Experimental analysis. Rheol. Acta 2000, 39, 444–451. [Google Scholar] [CrossRef]
- Venerus, D.C.; Kompani, M.; Bernstein, B. Equibiaxial extensional flow of polymer melts via lubricated squeezing flow. II. Flow modeling. Rheol. Acta 2000, 39, 574–582. [Google Scholar] [CrossRef]
- Jackson, J.D. A study of squeezing flow. Flow Turbul. Combust. 1963, 11, 148–152. [Google Scholar] [CrossRef]
- Smyrnaios, D.; Tsamopoulos, J. Squeeze flow of Bingham plastics. J. Non-Newton. Fluid Mech. 2001, 100, 165–189. [Google Scholar] [CrossRef]
- Alexandrou, A.N.; Florides, G.C.; Georgiou, G.C. Squeeze Flow of Semi-Solid Slurries. Solid State Phenom. 2012, 193, 103–115. [Google Scholar] [CrossRef]
- Muravleva, L. Squeeze plane flow of viscoplastic Bingham material. J. Non-Newton. Fluid Mech. 2015, 220, 148–161. [Google Scholar] [CrossRef]
- Muravleva, L. Axisymmetric squeeze flow of a viscoplastic Bingham medium. J. Non-Newton. Fluid Mech. 2017, 249, 97–120. [Google Scholar] [CrossRef]
- Muravleva, L. Squeeze flow of Bingham, Casson and Herschel-Bulkley fluids with yield slip at the wall by accelerated augmented Lagrangian method. J. Non-Newton. Fluid Mech. 2020, 282, 104320. [Google Scholar] [CrossRef]
- Fusi, L.; Farina, A.; Rosso, F. Planar squeeze flow of a bingham fluid. J. Non-Newton. Fluid Mech. 2015, 225, 1–9. [Google Scholar] [CrossRef]
- Fusi, L.; Farina, A.; Rosso, F. Squeeze flow of a Bingham-type fluid with elastic core. Int. J. Non-Newton. Fluid Mech. 2016, 78, 59–65. [Google Scholar] [CrossRef]
- Sherwood, J.; Durban, D. Squeeze flow of a power-law viscoplastic solid. J. Non-Newton. Fluid Mech. 1996, 62, 35–54. [Google Scholar] [CrossRef]
- Sherwood, J.; Durban, D. Squeeze-flow of a Herschel–Bulkley fluid. J. Non-Newton. Fluid Mech. 1998, 77, 115–121. [Google Scholar] [CrossRef]
- Adams, M.; Aydin, I.; Briscoe, B.; Sinha, S. A finite element analysis of the squeeze flow of an elasto-viscoplastic paste material. J. Non-Newton. Fluid Mech. 1997, 71, 41–57. [Google Scholar] [CrossRef]
- Lawal, A.; Kalyon, D.M. Squeezing flow of viscoplastic fluids subject to wall slip. Polym. Eng. Sci. 1998, 38, 1793–1804. [Google Scholar] [CrossRef]
- Muravleva, L. Axisymmetric squeeze flow of a Casson medium. J. Non-Newton. Fluid Mech. 2019, 267, 35–50. [Google Scholar] [CrossRef]
- Kaushik, P.; Mondal, P.K.; Chakraborty, S. Flow dynamics of a viscoelastic fluid squeezed and extruded between two parallel plates. J. Non-Newton. Fluid Mech. 2016, 227, 56–64. [Google Scholar] [CrossRef]
- Phan-Thien, N. Sliding and squeezing flow of a viscoelastic fluid in a wedge. Math. Und. Phys. 1990, 41, 431–440. [Google Scholar] [CrossRef]
- Oliver, D.R. The influence of fluid inertia, viscosity and extra stress on the load bearing capacity of a squeeze film of oil. Appl. Sci. Res. 1979, 35, 217–235. [Google Scholar] [CrossRef]
- Engmann, J.; Servais, C.; Burbidge, A.S. Squeeze flow theory and applications to rheometry: A review. J. Non-Newton. Fluid Mech. 2005, 132, 1–27. [Google Scholar] [CrossRef]
- McClelland, M.A.; Finlayson, B.A. Squeezing flow of elastic liquids. J. Non-Newton. Fluid Mech. 1983, 13, 181–201. [Google Scholar] [CrossRef]
- Dienes, G.J.; Klemm, H.F. Theory and Application of the Parallel Plate Plastometer. J. Appl. Phys. 1946, 17, 458–471. [Google Scholar] [CrossRef]
- Gent, A.N. Theory of the parallel plate viscometer. Br. J. Appl. Phys. 1960, 11, 85–87. [Google Scholar] [CrossRef]
- Grimm, R.J. Squeezing flows of polymeric liquids. AIChE J. 1978, 24, 427–439. [Google Scholar] [CrossRef]














| 65 | 10 | 32.5 | 32.5 | 2 | 5 | 5.4 | 85 |
| Rubber Compound | TTI | TTS | TTT |
|---|---|---|---|
| Viscosity (MPa·s) | 0.24 | 0.22 | 0.21 |
| Rubber Compound | TTI | TTS | TTT |
|---|---|---|---|
| Sliding friction coefficient * | 1.0 ± 0.015 | 0.9 ± 0.01 | 1.0 ± 0.021 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, Y.; Pan, Y.; Hu, X.; Yu, F. Squeezing Mechanical Analysis and Model Establishment of the Viscoelastic Rubber-Strip-Feeding Process of the Cold-Feed Rubber Extruder. Polymers 2022, 14, 3602. https://doi.org/10.3390/polym14173602
Liu Y, Pan Y, Hu X, Yu F. Squeezing Mechanical Analysis and Model Establishment of the Viscoelastic Rubber-Strip-Feeding Process of the Cold-Feed Rubber Extruder. Polymers. 2022; 14(17):3602. https://doi.org/10.3390/polym14173602
Chicago/Turabian StyleLiu, Yanchang, Yiren Pan, Xuehua Hu, and Fang Yu. 2022. "Squeezing Mechanical Analysis and Model Establishment of the Viscoelastic Rubber-Strip-Feeding Process of the Cold-Feed Rubber Extruder" Polymers 14, no. 17: 3602. https://doi.org/10.3390/polym14173602
APA StyleLiu, Y., Pan, Y., Hu, X., & Yu, F. (2022). Squeezing Mechanical Analysis and Model Establishment of the Viscoelastic Rubber-Strip-Feeding Process of the Cold-Feed Rubber Extruder. Polymers, 14(17), 3602. https://doi.org/10.3390/polym14173602