Quality Definition in Micro Injection Molding Process by Means of Surface Characterization Parameters
Abstract
:1. Introduction
2. Materials and Methods
2.1. Mold Design and Manufacturing
2.2. Material and Micro-IM Machine
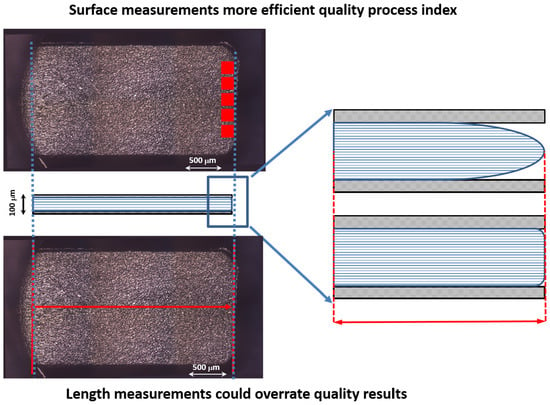
2.3. Optical Measurements for Length and Surface Parts Characterization
2.4. Mold Characterization
3. Experimental Plan and Methodology
4. Results and Discussion
4.1. Case A: Evaluating Steady State Condition of the Process
4.2. Case A: Evaluating Effective Surface Parameters
4.3. Case B: Products and Process Quality Evaluation by Means of Dimensional and Surface Parameters
4.3.1. Dimensional Quality Index: Part Length
4.3.2. Surface Quality Index
4.4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Usman Jan, Q.M.; Habib, T.; Noor, S.; Abas, M.; Azim, S.; Yaseen, Q.M. Multi Response Optimization of Injection Moulding Process Parameters of Polystyrene and Polypropylene to Minimize Surface Roughness and Shrinkage’s Using Integrated Approach of S/N Ratio and Composite Desirability Function. Cogent Eng. 2020, 7, 1781424. [Google Scholar] [CrossRef]
- Chen, C.P.; Chuang, M.T.; Hsiao, Y.H.; Yang, Y.K.; Tsai, C.H. Simulation and Experimental Study in Determining Injection Molding Process Parameters for Thin-Shell Plastic Parts via Design of Experiments Analysis. Expert Syst. Appl. 2009, 36, 10752–10759. [Google Scholar] [CrossRef]
- Huang, M.S.; Li, C.J.; Yu, J.C.; Huang, Y.M.; Hsieh, L.C. Robust Parameter Design of Micro-Injection Molded Gears Using a LIGA-like Fabricated Mold Insert. J. Mater. Process. Technol. 2009, 209, 5690–5701. [Google Scholar] [CrossRef]
- Bensingh, R.J.; Machavaram, R.; Boopathy, S.R.; Jebaraj, C. Injection Molding Process Optimization of a Bi-Aspheric Lens Using Hybrid Artificial Neural Networks (ANNs) and Particle Swarm Optimization (PSO). Meas. J. Int. Meas. Confed. 2019, 134, 359–374. [Google Scholar] [CrossRef]
- Attia, U.M.; Alcock, J.R. Evaluating and Controlling Process Variability in Micro-Injection Moulding. Int. J. Adv. Manuf. Technol. 2011, 52, 183–194. [Google Scholar] [CrossRef]
- Bellantone, V.; Surace, R.; Trotta, G.; Fassi, I. Replication Capability of Micro Injection Moulding Process for Polymeric Parts Manufacturing. Int. J. Adv. Manuf. Technol. 2013, 67, 1407–1421. [Google Scholar] [CrossRef]
- Tosello, G.; Hansen, H.N.; Dormann, B.; Decker, C.; Guerrier, P. Process Control and Product Evaluation in Micro Molding Using a Screwless/Two-Plunger Injection Unit. In Proceedings of the ANTEC, Orlando, FL, USA, 17–19 May 2010; Volume 3, pp. 1947–1952. [Google Scholar]
- Quadrini, F.; Bellisario, D.; Santo, L.; Bottini, L.; Boschetto, A. Mold Replication in Injection Molding of High Density Polyethylene. Polym. Eng. Sci. 2020, 60, 2459–2469. [Google Scholar] [CrossRef]
- Bellantone, V.; Surace, R.; Modica, F.; Fassi, I. Evaluation of Mold Roughness Influence on Injected Thin Micro-Cavities. Int. J. Adv. Manuf. Technol. 2018, 94, 4565–4575. [Google Scholar] [CrossRef]
- Surace, R.; Sorgato, M.; Bellantone, V.; Modica, F.; Lucchetta, G.; Fassi, I. Effect of Cavity Surface Roughness and Wettability on the Filling Flow in Micro Injection Molding. J. Manuf. Process. 2019, 43, 105–111. [Google Scholar] [CrossRef]
- Zhao, J.; Mayes, R.H.; Chen, G.; Xie, H.; Chan, P.S. Effects of Process Parameters on the Micro Molding Process. Polym. Eng. Sci. 2003, 43, 1542–1554. [Google Scholar] [CrossRef]
- Sha, B.; Dimov, S.; Griffiths, C.; Packianather, M.S. Investigation of Micro-Injection Moulding: Factors Affecting the Replication Quality. J. Mater. Process. Technol. 2007, 183, 284–296. [Google Scholar] [CrossRef]
- Whiteside, B.R.; Martyn, M.T.; Coates, P.D.; Allan, P.S.; Hornsby, P.R.; Greenway, G.; Greenaway, G. Micromoulding: Process Characteristics and Product Properties. Plast. Rubber Compos. 2003, 32, 231–239. [Google Scholar] [CrossRef]
- Yao, D.; Kim, B. Scaling Issues in Miniaturization of Injection Molded Parts. J. Manuf. Sci. Eng. 2004, 126, 733. [Google Scholar] [CrossRef]
- Whitehouse, D.J. Surface Metrology. Meas. Sci. Technol. 1997, 8, 955–972. [Google Scholar] [CrossRef]
- Tosello, G.; Haitjema, H.; Leach, R.K.; Quagliotti, D.; Gasparin, S.; Hansen, H.N. An International Comparison of Surface Texture Parameters Quantification on Polymer Artefacts Using Optical Instruments. CIRP Ann.-Manuf. Technol. 2016, 65, 529–532. [Google Scholar] [CrossRef]
- Flugge, J.; Wendt, K.; Danzebrink, H.; Abou-zeid, A. Optical Methods for Dimensional Metrology in Production Engineering. CIRP Ann.-Manuf. Technol. 2002, 51, 685–699. [Google Scholar]
- Zhang, H.; Zhang, N.; Han, W.; Gilchrist, M.D.; Fang, F. Precision Replication of Microlens Arrays Using Variotherm-Assisted Microinjection Moulding. Precis. Eng. 2021, 67, 248–261. [Google Scholar] [CrossRef]
- Zolfaghari, A.; Zhang, L.; Zhou, W.; Yi, A.Y. Replication of Plastic Microlens Arrays Using Electroforming and Precision Compression Molding. Microelectron. Eng. 2021, 239–240, 111529. [Google Scholar] [CrossRef]
- Loaldi, D.; Regi, F.; Li, D.; Giannekas, N.; Calaon, M.; Zhang, Y.; Tosello, G. Product Fingerprints for the Evaluation of Tool/Polymer Replication Quality in Injection Molding at the Micro/Nano Scale. Nanomanuf. Metrol. 2021, 4, 278–288. [Google Scholar] [CrossRef]
- Guo, G. Investigation on Surface Roughness of Injection Molded Polypropylene Parts with 3D Optical Metrology. Int. J. Interact. Des. Manuf. 2022, 16, 17–23. [Google Scholar] [CrossRef]
- Das, J.; Linke, B. Evaluation and Systematic Selection of Significant Multi-Scale Surface Roughness Parameters (SRPs) as Process Monitoring Index. J. Mater. Process. Technol. 2017, 244, 157–165. [Google Scholar] [CrossRef] [Green Version]
- Yao, D.; Kim, B. Injection Molding High Aspect Ratio Microfeatures. J. Inject. Molding Technol. 2002, 6, 11–17. [Google Scholar]
- Gao, W.; Haitjema, H.; Fang, F.Z.; Leach, R.K.; Cheung, C.F.; Savio, E.; Linares, J.M. On-Machine and in-Process Surface Metrology for Precision Manufacturing. CIRP Ann. 2019, 68, 843–866. [Google Scholar] [CrossRef] [Green Version]
- Whitehouse, D.J. Handbook of Surface and Nanometrology; CRC Press: Boca Raton, FL, USA, 2010; ISBN 9780429140693. [Google Scholar]
- ISO 25178-2:2021; Geometrical Product Specifications (GPS)—Surface Texture: Areal—Part 2: Terms, Definitions and Surface Texture Parameters. ISO: Geneva, Switzerland, 2021.
- Taylor, J.R. An Introduction to Error Analysis: The Study of Uncertainties in Physical Measurements; ASMSU/Spartans.4.Spartans Textbook; University Science Books: Melville, NY, USA, 1997; ISBN 9780935702422. [Google Scholar]
- Montgomery, D.C. Design and Analysis of Experiments, 8th ed.; Wiley: Hoboken, NJ, USA, 2012; ISBN 978-1118-14692-7. [Google Scholar]
- Montgomery, D.C. Statistical Quality Control: A Modern Introduction; J. Wiley: Hoboken, NJ, USA, 2019. [Google Scholar]













| Name | Trade Name | Grade | Manufacturer | MVR (cm3/10 min) | Density (kg/m3) |
|---|---|---|---|---|---|
| polyoxymethylene | Ultraform | N2320 003 | Basf | 7.5 | 1400 |
| L (µm) | Sa (µm) | Sq (µm) | Sz (µm) | Ssk | Sku | Sp | Sv | |
|---|---|---|---|---|---|---|---|---|
| Mold | 2579.4 | 2.1 | 3.2 | 25.8 | −1.9 | 6.1 | 14.7 | −11.1 |
| Tm (°C) | Tmo (°C) | Vinj (mm/s) | Piston Run (mm) | Ph (Mpa) | th (s) | tc (s) |
|---|---|---|---|---|---|---|
| 230 | 90 | 150–330 | 18.2 | 100 | 3 | 5 |
| Parameter | Description | Low Level −1 | Central Point 0 | High Level +1 |
|---|---|---|---|---|
| Tmo (°C) | Mold temperature | 90 | 95 | 100 |
| Tm (°C) | Melt temperature | 230 | 235 | 240 |
| Vinj (mm/s) | Injection velocity | 140–260 | 150–260 | 160–260 |
| StdOrder | RunOrder | CenterPt | Blocks | Tmold | Tmelt | Vinj |
|---|---|---|---|---|---|---|
| 15 | 1 | 1 | 1 | −1 | 1 | 1 |
| 9 | 2 | 1 | 1 | −1 | −1 | −1 |
| 14 | 3 | 1 | 1 | 1 | −1 | 1 |
| 5 | 4 | 1 | 1 | −1 | −1 | 1 |
| 6 | 5 | 1 | 1 | 1 | −1 | 1 |
| 16 | 6 | 1 | 1 | 1 | 1 | 1 |
| 13 | 7 | 1 | 1 | −1 | −1 | 1 |
| 8 | 8 | 1 | 1 | 1 | 1 | 1 |
| 2 | 9 | 1 | 1 | 1 | −1 | −1 |
| 3 | 10 | 1 | 1 | −1 | 1 | −1 |
| 11 | 11 | 1 | 1 | −1 | 1 | −1 |
| 10 | 12 | 1 | 1 | 1 | −1 | −1 |
| 17 | 13 | 0 | 1 | 0 | 0 | 0 |
| 12 | 14 | 1 | 1 | 1 | 1 | −1 |
| 4 | 15 | 1 | 1 | 1 | 1 | −1 |
| 7 | 16 | 1 | 1 | −1 | 1 | 1 |
| 1 | 17 | 1 | 1 | −1 | −1 | −1 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bellantone, V.; Surace, R.; Fassi, I. Quality Definition in Micro Injection Molding Process by Means of Surface Characterization Parameters. Polymers 2022, 14, 3775. https://doi.org/10.3390/polym14183775
Bellantone V, Surace R, Fassi I. Quality Definition in Micro Injection Molding Process by Means of Surface Characterization Parameters. Polymers. 2022; 14(18):3775. https://doi.org/10.3390/polym14183775
Chicago/Turabian StyleBellantone, Vincenzo, Rossella Surace, and Irene Fassi. 2022. "Quality Definition in Micro Injection Molding Process by Means of Surface Characterization Parameters" Polymers 14, no. 18: 3775. https://doi.org/10.3390/polym14183775
APA StyleBellantone, V., Surace, R., & Fassi, I. (2022). Quality Definition in Micro Injection Molding Process by Means of Surface Characterization Parameters. Polymers, 14(18), 3775. https://doi.org/10.3390/polym14183775