Hedgehog, Chamomile and Multipetal Polymeric Structures on the Nanoparticle Surface: Theoretical Insights
Abstract
:1. Introduction
2. Model
3. Free Energy
3.1. Hedgehog
3.2. Chamomile
3.3. Multipetal Structure
4. Equilibrium Parameters of the Structures and Free Energies Comparison
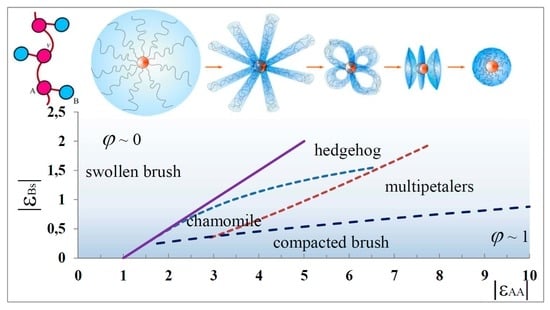
5. State Diagrams
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Doane, T.L.; Burda, C. The unique role of nanoparticles in nanomedicine: Imaging, drug delivery and therapy. Chem. Soc. Rev. 2012, 41, 2885–2911. [Google Scholar] [CrossRef]
- Elsabahy, M.; Wooley, K.L. Design of polymeric nanoparticles for biomedical delivery applications. Chem. Soc. Rev. 2012, 41, 2545–2561. [Google Scholar] [CrossRef] [Green Version]
- Gromadzki, D.; Rychter, P.; Uchman, M.; Momekova, D.; Marcinkowski, A.; Koseva, N.S.; El Fray, M.; Marić, M. Multifunctional amphiphilic nanoparticles featuring (bio)degradable core and dual-responsive shell as biomedical platforms for controlled release. Macromol. Chem. Phys. 2015, 216, 2287–2301. [Google Scholar] [CrossRef]
- Chauhan, P.S. Review of nanoparticle applications in petroleum engineering: Recent advancements and challenges. In Proceedings of the SPE-199778-STU, SPE Annual Technical Conference and Exhibition, Calgary, AB, Canada, 30 September–2 October 2019. [Google Scholar]
- Fakoya, M.F.; Shah, S.N. Enhancement of filtration properties in surfactant-based and polymeric fluids by nanoparticles. In Proceedings of the SPE- 171029-MS, SPE Eastern Regional Meeting, Charleston, WV, USA, 21–23 October 2014. [Google Scholar]
- Zoppe, J.O.; Ataman, N.C.; Mocny, P.; Wang, J.; Moraes, J.; Klok, H.-A. Surface-initiated controlled radical polymerization: State-of-the-art, opportunities, and challenges in surface and interface engineering with polymer brushes. Chem. Rev. 2017, 117, 1105–1318. [Google Scholar] [CrossRef] [Green Version]
- Lin, J.; Zhang, H.; Morovati, V.; Dargazany, R. PEGylation on mixed monolayer gold nanoparticles: Effect of grafting density, chain length, and surface curvature. J. Colloid Interface Sci. 2017, 504, 325–333. [Google Scholar] [CrossRef]
- Wu, L.; Glebe, U.; Boker, A. Surface-initiated controlled radical polymerizations from silica nanoparticles, gold nanocrystals, and bionanoparticles. Polym. Chem. 2015, 6, 5143–5184. [Google Scholar] [CrossRef] [Green Version]
- Hore, M.J.A. Polymers on nanoparticles: Structure & Dynamics. Soft Matter 2019, 15, 1120–1134. [Google Scholar]
- Chancellor, A.J.; Seymour, B.T.; Zhao, B. Characterizing polymer-grafted nanoparticles: From basic defining parameters to behavior in solvents and self-assembled structures. Anal. Chem. 2019, 91, 6391–6402. [Google Scholar] [CrossRef] [Green Version]
- Fujii, S.; Suzaki, M.; Nakamura, Y.; Sakai, K.; Ishida, N.; Biggs, S. Surface characterization of nanoparticles carrying ph-responsive polymer hair. Polymer 2010, 51, 6240–6247. [Google Scholar] [CrossRef]
- Zhang, Q.; Liao, Y.; He, L.; Bu, W. Spherical Polymer brushes in solvents of variable quality: An experimental insight by TEM imaging. Langmuir 2013, 29, 4181–4186. [Google Scholar] [CrossRef]
- Yana, J.; Bockstaller, M.R.; Matyjaszewski, K. Brush-modified materials: Control of molecular architecture, assembly behavior, properties and applications. Prog. Polym. Sci. 2020, 100, 101180. [Google Scholar] [CrossRef]
- Eriksson, M.; Hamers, J.; Peijs, T.; Goossens, H. The influence of graft length and density on dispersion, crystallisation and rheology of poly(ε-caprolactone)/silica nanocomposites. Molecules 2019, 24, 2106. [Google Scholar] [CrossRef] [Green Version]
- Chastek, T.T.; Hudson, S.D.; Hackley, V.A. Preparation and characterization of patchy particles. Langmuir 2008, 24, 13897–13903. [Google Scholar] [CrossRef]
- Varadharajan, D.; Turgut, H.; Lahann, J.; Yabu, H.; Delaittre, G. Surface-reactive patchy nanoparticles and nanodiscs prepared by tandem nanoprecipitation and internal phase separation. Adv. Funct. Mater. 2018, 28, 1800846. [Google Scholar] [CrossRef]
- Asai, M.; Cacciuto, A.; Kumar, S.K. Quantitative analogy between polymer-grafted nanoparticles and patchy particles. Soft Matter 2015, 11, 793–797. [Google Scholar] [CrossRef]
- Modica, K.J.; Martin, T.B.; Jayaraman, A. Effect of polymer architecture on the structure and interactions of polymer grafted particles: Theory and simulations. Macromolecules 2017, 50, 4854–4866. [Google Scholar] [CrossRef]
- Coleman, B.R.; Moffitt, M.G. Amphiphilic inorganic nanoparticles with mixed polymer brush layers of variable composition: Bridging the paradigms of block copolymer and nanoparticle self-assembly. Chem. Mater. 2018, 30, 2474–2482. [Google Scholar] [CrossRef]
- Tan, K.Y.; Ramstedt, M.; Colak, B.; Huck, W.T.S.; Gautrot, J.E. Study of thiol-ene chemistry on polymer brushes and application to surface patterning and protein adsorption. Polym. Chem. 2016, 7, 979–990. [Google Scholar] [CrossRef]
- Liu, X.; Yang, Y.; Urban, M.W. Stimuli-responsive polymeric nanoparticle. Macromol. Rapid Commun. 2017, 38, 1700030. [Google Scholar] [CrossRef] [Green Version]
- Chen, K.; Cao, L.; Zhang, Y.; Li, K.; Qin, X.; Guo, X. Conformation study of dual stimuli-responsive core-shell diblock polymer brushes. Polymers 2018, 10, 1084. [Google Scholar] [CrossRef] [Green Version]
- Appel, E.A.; Tibbitt, M.W.; Webber, M.J.; Mattix, B.A.; Veiseh, O.; Lange, R. Self-assembled hydrogels utilizing polymer–nanoparticle interactions. Nat. Commun. 2015, 6, 6295. [Google Scholar] [CrossRef]
- Narupai, B.; Poelma, J.E.; Pester, C.W.; McGrath, A.J.; Toumayan, E.P.; Luo, Y.; Kramer, J.W.; Clark, P.G.; Ray, P.C.; Hawker, C.J. Hierarchical comb brush architectures via sequential light-mediated controlled radical polymerizations. J. Polym Sci. A Polym. Chem. 2016, 54, 2276–2284. [Google Scholar] [CrossRef]
- Zou, H.; Wu, S.; She, J. Polymer/Silica nanocomposites: Preparation, characterization, properties, and applications. Chem. Rev. 2008, 108, 3893–3957. [Google Scholar] [CrossRef] [PubMed]
- Lin, Y.; Hu, S.; Wu, G. Structure, dynamics, and mechanical properties of polyimide-grafted silica nanocomposites. J. Phys. Chem. C 2019, 123, 6616–6626. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, Z.; He, Y.; Yoon, Y.J.; Jung, J.; Zhang, G.; Lin, Z. Light-enabled reversible self-assembly and tunable optical properties of stable hairy nanoparticles. Proc. Natl. Acad. Sci. USA 2018, 115, E1391–E1400. [Google Scholar] [CrossRef] [Green Version]
- Verso, F.L.; Yelash, L.; Egorov, S.A.; Binder, K. Effect of the solvent quality on the structural rearrangement of spherical brushes: Coarse-grained models. Soft Matter 2012, 8, 4185. [Google Scholar] [CrossRef]
- Gong, M.; Yu, Q.; Wang, C.; Wang, R. Simulating surface patterning of nanoparticles by polymers via dissipative particle dynamics method. Langmuir 2019, 35, 5534–5540. [Google Scholar] [CrossRef]
- Yi, C.; Yang, Y.; Liu, B.; He, J.; Nie, Z. Polymer-guided assembly of inorganic nanoparticles. Chem. Soc. Rev. 2020, 49, 465. [Google Scholar] [CrossRef]
- Chen, C.; Tang, P.; Qiu, F. Binary hairy nanoparticles: Recent progress in theory and simulations. J. Polym. Sci. B Polym. Phys. 2014, 52, 1583–1599. [Google Scholar] [CrossRef]
- Malho, J.; Morits, M.; Löbling, T.I.; Majoinen, N.J.; Schacher, F.H.; Ikkala, O.; Gröschel, A.H. Rod-like nanoparticles with striped and helical topography. ACS Macro Lett. 2016, 5, 1185–1190. [Google Scholar] [CrossRef]
- Löbling, T.I.; Haataja, J.S.; Synatschke, C.V.; Schacher, F.H.; Müller, M.; Hanisch, A.; Gröschel, A.H.; Müller, H.E. Hidden structural features of multicompartment micelles revealed by cryogenic transmission electron tomography. ACS Nano 2014, 8, 11330–11340. [Google Scholar] [CrossRef] [PubMed]
- Synatschke, C.V.; Nomoto, T.; Cabral, H.; Fortsch, M.; Toh, K.; Matsumoto, Y.; Miyazaki, K.; Hanisch, A.; Schacher, F.H.; Kishimura, A.; et al. Multicompartment micelles with adjustable poly(ethylene glycol) shell for efficient in vivo photodynamic therapy. ACS Nano 2014, 8, 1161–1172. [Google Scholar] [CrossRef] [PubMed]
- Pu, W.-F.; Ushakova, A.; Liu, R.; Lazutin, A.A.; Vasilevskaya, V.V. Self-assembly in amphiphilic spherical brushes. J. Chem. Phys. 2020, 152, 234903. [Google Scholar] [CrossRef]
- Ushakova, A.S.; Lazutin, A.A.; Vasilevskaya, V.V. Flowerlike multipetal structures of nanoparticles decorated by amphiphilic homopolymers. Macromolecules 2021, 54, 6285–6295. [Google Scholar] [CrossRef]
- Lazutin, A.A.; Vasilevskaya, V.V. Matrix free polymer nanocomposites from amphiphilic hairy nanoparticles: Solvent selectivity and mechanical properties. Polymer 2022, 255, 125172. [Google Scholar] [CrossRef]
- Qiao, L.; Kaifeng, D. Magnetic field-induced self-assembly of urchin-like polymeric particles: Mechanism, dispersity, and application in wastewater treatment. Sep. Purif. Technol. 2022, 299, 121742. [Google Scholar] [CrossRef]
- Montjoy, D.G.; Hou, H.; Bahng, J.H.; Eskafi, A.; Kotov, N.A. Photocatalytic omnidispersible microscale colloids with nanoscale polymeric spikes. Chem. Mater. 2020, 32, 9897–9905. [Google Scholar] [CrossRef]
- Montjoy, D.G.; Hou, H.; Bahng, J.H.; Eskafi, A.; Jiang, R.; Kotov, N.A. Photocatalytic hedgehog particles for high ionic strength environments. ACS Nano 2021, 15, 4226–4234. [Google Scholar] [CrossRef]
- Vasilevskaya, V.V.; Khalatur, P.G.; Khokhlov, A.R. Conformational polymorphism of amphiphilic polymers in a poor solvent. Macromolecules 2003, 36, 10103–10111. [Google Scholar] [CrossRef]
- Savariar, E.N.; Aathimanikandan, S.V.; Thayumanavan, S. Supramolecular assemblies from amphiphilic homopolymers: Testing the scope. J. Am.Chem. Soc. 2006, 128, 16224–16230. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Vasilevskaya, V.V.; Govorun, E.N. Hollow and vesicle particles from macromolecules with amphiphilic monomer units. Polym. Rev. 2019, 59, 625–650. [Google Scholar] [CrossRef]
- Zhang, J.; Liu, K.; Mullen, K.; Yin, M. Self-assemblies of amphiphilic homopolymers: Synthesis, morphology studies and biomedical applications. Chem. Commun. 2015, 51, 11541–11555. [Google Scholar] [CrossRef]
- Gartner, T.E.; Jayaraman, A. Modeling and simulations of polymers: A roadmap. Macromolecules 2019, 52, 755–786. [Google Scholar] [CrossRef] [Green Version]
- Larin, D.E.; Lazutin, A.A.; Govorun, E.N.; Vasilevskaya, V.V. Self-assembly into strands in amphiphilic polymer brushes. Langmuir 2016, 32, 7000–7008. [Google Scholar] [CrossRef] [PubMed]
- Lazutin, A.A.; Kosmachev, A.N.; Vasilevskaya, V.V. Lamellae and parking garage structures in amphiphilic homopolymer brushes with different grafting densities. J. Chem. Phys. 2019, 151, 154903. [Google Scholar] [CrossRef]
- Buglakov, A.I.; Larin, D.E.; Vasilevskaya, V.V. Orientation- and cosolvent-induced self-assembly of amphiphilic homopolymers in selective solvents. Polymer 2021, 232, 0032–3861. [Google Scholar] [CrossRef]
- Lifshits, I.M.; Grosberg, A.Y.; Khokhlov, A.R. Some problems of the statistical physics of polymer chains with volume interaction. Rev. Mod. Phys. 1978, 50, 683. [Google Scholar] [CrossRef]
- Helfrich, W. Elastic properties of lipid bilayers: Theory and possible experiments. Z. Fur Nat. C 1973, 28, 693–703. [Google Scholar] [CrossRef] [PubMed]
- Helfrich, W. Steric interaction of fluid membranes in multilayer systems. Z. Für Nat. A 1978, 33, 305–315. [Google Scholar] [CrossRef]
- Helfrich, W.; Servuss, R.-M. Undulations, steric interaction and cohesion of fluid membranes. Il Nuovo Cimento D 1984, 3, 137–151. [Google Scholar] [CrossRef]
- Maresov, E.A.; Semenov, A.N. Mesoglobule morphologies of amphiphilic polymers. Macromolecules 2008, 41, 9439–9457. [Google Scholar] [CrossRef]
- Ushakova, A.S.; Govorun, E.N.; Khokhlov, A.R. Globules of amphiphilic macromolecules. J. Phys. Cond. Matter 2006, 18, 915–929. [Google Scholar] [CrossRef]
- Mikhailov, I.V.; Darinskii, A.A.; Birshtein, T.M. Bending rigidity of branched polymer brushes with finite membrane thickness. Polym. Sci. Ser. C 2022. [Google Scholar] [CrossRef]








Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ushakova, A.S.; Vasilevskaya, V.V. Hedgehog, Chamomile and Multipetal Polymeric Structures on the Nanoparticle Surface: Theoretical Insights. Polymers 2022, 14, 4358. https://doi.org/10.3390/polym14204358
Ushakova AS, Vasilevskaya VV. Hedgehog, Chamomile and Multipetal Polymeric Structures on the Nanoparticle Surface: Theoretical Insights. Polymers. 2022; 14(20):4358. https://doi.org/10.3390/polym14204358
Chicago/Turabian StyleUshakova, Aleksandra S., and Valentina V. Vasilevskaya. 2022. "Hedgehog, Chamomile and Multipetal Polymeric Structures on the Nanoparticle Surface: Theoretical Insights" Polymers 14, no. 20: 4358. https://doi.org/10.3390/polym14204358
APA StyleUshakova, A. S., & Vasilevskaya, V. V. (2022). Hedgehog, Chamomile and Multipetal Polymeric Structures on the Nanoparticle Surface: Theoretical Insights. Polymers, 14(20), 4358. https://doi.org/10.3390/polym14204358