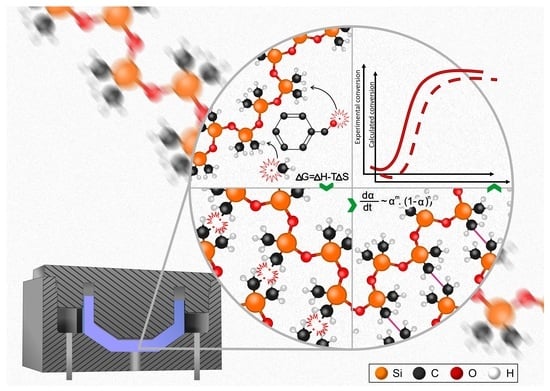
Peroxide-Based Crosslinking of Solid Silicone Rubber, Part I: Insights into the Influence of Dicumylperoxide Concentration on the Curing Kinetics and Thermodynamics Determined by a Rheological Approach
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials
2.2. Rotational Rheometry
3. Theoretical Background
3.1. Crosslinking Kinetic Modelling
3.2. Peroxide-Based Crosslinking Mechanism of PDMS
- i
- ii
- iii
- –O––O–
- iv
- –O––O–
- v
- –O––O–––O–
- vi
- vii
- –O–=–O––
- viii
- –O–=–O––
- viiii
- –O––⟶–
4. Results
4.1. Curing Characteristics
4.2. Crosslinking Kinetics
4.3. Thermodynamic Reasoning behind the Dicumylperoxide-Based Crosslinking Reaction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Preexponential factor | |
| DCP | Dicumylperoxide |
| DSC | Differential scanning calorimetry |
| h | Planck constant |
| Enthalpy change | |
| Activation energy | |
| NMR | Proton-1 nuclear magnetic resonance |
| Arrhenius rate constant | |
| Boltzmann constant | |
| m | Autocatalytic reaction order |
| MH | Maximum detected torque |
| ML | Minimum detected torque |
| Molecular weight of a chain | |
| Number average molecular weight | |
| Weight average molecular weight | |
| Z-average molecular weight | |
| Z+1-average molecular weight | |
| n | -order reaction order |
| Number of chains of a specific molecular weight | |
| PDMS | Poly(dimethylsixolane) |
| phr | Parts per hundred rubber |
| ppm | Parts per million |
| R | Molar gas constant |
| RPA | Rubber process analyser |
| RSE | Radical stabilization energy |
| Entropy change | |
| T | Temperature |
| t | Time |
| Scorch time | |
| Optimum cure time | |
| TGA | Thermogravimetric analysis |
| Conversion | |
| Chemical shift |
Appendix A
Appendix A.1. Determination of the Molecular Weight
| Sample | ||||||
|---|---|---|---|---|---|---|
| A | 373,887 | 677,037 | 1,043,506 | 1,397,882 | 1.81081 | 1.54128 |
| B | 365,736 | 650,012 | 1,007,852 | 1,356,495 | 1.77727 | 1.55051 |
| C | 358,198 | 647,947 | 1,015,985 | 1,377,667 | 1.80891 | 1.56801 |
| Mean | 365,940 | 658,330 | 1,022,450 | 1,377,350 | 1.799 | 1.553 |
| ± std. dev | ±6406 | ±13,253 | ±15,256 | ±16,896 | ±0.015 | ±0.011 |

Appendix A.2. Determination of the Filler Content

Appendix A.3. Determination of the Vinyl Content


References
- Shit, S.; Shah, P. A Review on Silicone Rubber. Natl. Acad. Sci. Lett. 2013, 36, 355–365. [Google Scholar] [CrossRef]
- Calderón, J.; López, D.; Pérez, E.; Montesinos, J. Polysiloxanes as polymer matrices in biomedical engineering: Their interesting properties as the reason for the use in medical sciences. Polym. Bull. 2020, 77, 2749–2817. [Google Scholar] [CrossRef]
- Fink, J. Liquid Silicone Rubber: Chemistry, Materials, and Processing; John Wiley & Sons: Hoboken, NJ, USA, 2019. [Google Scholar]
- Kim, D.; Park, J.; Lee, D.; Seo, K. Correlation between the Crosslink Characteristics and Mechanical Properties of Natural Rubber Compound via Accelerators and Reinforcement. Polymers 2020, 12, 2020. [Google Scholar] [CrossRef]
- Nardelli, F.; Calucci, L.; Carignani, E.; Borsacchi, S.; Cettolin, M.; Arimondi, M.; Giannini, L.; Geppi, M.; Martini, F. Influence of Sulfur-Curing Conditions on the Dynamics and Crosslinking of Rubber NEtworks: A Time-Domain NMR Study. Polymers 2022, 14, 767. [Google Scholar] [CrossRef] [PubMed]
- Kruželák, J.; Hložeková, K.; Kvasnicáková, A.; Tomanová, K.; Hudec, I. Application of Sulfur and Peroxide Curing Systems for Cross-Linking of Rubber Composites Filled with Calcium Lignosulfonate. Polymers 2022, 14, 1921. [Google Scholar] [CrossRef]
- Heideman, G.; Datta, R.; Noodermeer, J.; van Baarle, B. Activators in Accelerated Sulfur Vulcanization. Rubber Chem. Technol. 2004, 77, 512–541. [Google Scholar] [CrossRef]
- Traintinger, M.; Kerschbaumer, R.; Lechner, B.; Friesenbichler, W.; Lucyshyn, T. Temperature Profile in Rubber Injection Molding: Application of a Recently Developed Testing Method to Improve the Process Simulation and Calculation of Curing Kinetics. Polymers 2021, 13, 380. [Google Scholar] [CrossRef]
- Stieger, S.; Mitsoulis, E.; Walluch, M.; Ebner, C.; Kerschbaumer, R.; Haselmann, M.; Mostafaiyan, M.; Kämpfe, M.; Kühnert, I.; Wießner, S.; et al. On the Influence of Viscoelastic Modeling in Fluid Flow Simulations of Gum Acrylonitrile Butadiene Rubber. Polymers 2021, 13, 2323. [Google Scholar] [CrossRef]
- Bont, M.; Barry, C.; Johnston, S. A review of liquid silicone rubber injection molding: Process variables and process modeling. Polym. Eng. Sci. 2021, 61, 331–347. [Google Scholar] [CrossRef]
- Ou, H.; Sahli, M.; Barrière, T.; Gelin, J.C. Multiphysics modelling and experimenal investigations of the filling and curing phases of bi-injection moulding of thermoplastics polymer/liquid silicone rubbers. Polym. Eng. Sci. 2017, 92, 3871–3882. [Google Scholar]
- Lucyshyn, T.; D’Avernas, L.V.; Holzer, C. Influence of the Mold Property on the Injection Molding Cycle Time and Warpage Depending on the Polymer Processed. Polymers 2021, 13, 3196. [Google Scholar] [CrossRef]
- Bardelli, T.; Marano, C.; Vangosa, F. Polydimethylsiloxane crosslinking kinetics: A systematic study on Sylgard184 comparing rheological and thermal approaches. J. Appl. Polym. Sci. 2021, 138, 51013. [Google Scholar] [CrossRef]
- Hong, I.K.; Lee, S. Cure kinetics and modeling the reaction of silicone rubber. J. Ind. Eng. Chem. 2013, 19, 42–47. [Google Scholar] [CrossRef]
- Jalkanen, T. Isoconversional kinetic analysis for determining the rate of cross-linking for Pt and peroxide cure silicone rubbers. Thermochim. Acta 2021, 703, 178982. [Google Scholar] [CrossRef]
- Karami, Z.; Jazani, O.; Navarchian, A.; Saeb, M. Cure Kinetics of Silicone/Halloysite Nanotube Composites. J. Vinyl Addit. Technol. 2020, 26, 548–565. [Google Scholar] [CrossRef]
- Ke, Q.; Wu, C.; Chen, X. Model-free cure kinetics of additional liquid silicone rubber. Thermochim. Acta 2020, 688, 178584. [Google Scholar] [CrossRef]
- Hernández-Ortiz, J.; Osswald, T. Modeling processing of silicone rubber: Liquid versus hard silicone rubbers. J. Appl. Polym. Sci. 2011, 119, 1864–1871. [Google Scholar] [CrossRef]
- ASTM D5289-19a; Standard Test Method for Rubber Property—Vulcanization Using Rotorless Cure Meters. American Society for Testing and Materials: West Conshohocke, PA, USA, 2019.
- ASTM D6204-19a; Standard Test Method for Rubber—Measurement of Unvulcanized Rheological Properties Using Rotorless Shear Rheometers. American Society for Testing and Materials: West Conshohocke, PA, USA, 2019.
- ASTM D6601-19; Standard Test Method for Rubber Properties—Measurement of Cure and After—Cure Dynamic Properties Using a Rotorless Shear Rheometer. American Society for Testing and Materials: West Conshohocke, PA, USA, 2019.
- ASTM D8059-19; Standard Test Method for Rubber Compounds—Measurement of Unvulcanized Dynamic Strain Softening (Payne Effect) Using Sealed Cavity Rotorless Shear Rheometers. American Society for Testing and Materials: West Conshohocke, PA, USA, 2019.
- Marquardt, D. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. J. Soc. Indust. App. Math. 1963, 11, 431–441. [Google Scholar] [CrossRef]
- ASTM E2041-13(2018); Standard Test Method for Estimating Kinetic Parameters by Differential Scanning Calorimeter Using the Borchardt and Daniels Method. American Society for Testing and Materials: West Conshohocke, PA, USA, 2018.
- ASTM E698-18; Standard Test Method for Kinetic Parameters for Thermally Unstable Materials Using Differential Scanning Calorimetry and the Flynn/Wall/Ozawa Method. American Society for Testing and Materials: West Conshohocke, PA, USA, 2018.
- ASTM E2781-11; Standard Practice for Evaluation of Methods for Determination of Kinetic Parameters by Thermal Analysis. American Society for Testing and Materials: West Conshohocke, PA, USA, 2016.
- Vyazovkin, S.; Burnham, A.; Criado, J.; Pérez-Maqueda, L.; Popescu, C.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for performing kinetic computations on thermal analysis data. Thermochim. Acta 2011, 520, 1–19. [Google Scholar] [CrossRef]
- Vyazovkin, S. A time to search: Finding the meaning of variable activation energy. Phys. Chem. Chem. Phys. 2016, 18, 18643–18656. [Google Scholar] [CrossRef]
- Vyazovkin, S. Kissinger Method in Kinetics of Materials: Things to Beware and Be Aware of. Molecules 2020, 25, 2813. [Google Scholar] [CrossRef] [PubMed]
- Vyazovkin, S.; Burnham, A.; Favergeon, L.; Koga, N.; Moukhina, E.; Pérez-Maqueda, L.; Sbirrazzuoli, N. ICTAC Kinetics Committee recommendations for analysis of multi-step kinetics. Thermochim. Acta 2020, 689, 178597. [Google Scholar] [CrossRef]
- Vyazovkin, S. Determining Preexponential Factor in Model-Free Kinetic Methods: How and Why? Molecules 2021, 26, 3077. [Google Scholar] [CrossRef] [PubMed]
- Lang, M.; Hirner, S.; Wiesbrock, F.; Fuchs, P. A Review on Modeling Cure Kinetics and Mechanisms of Photopolymerization. Polymers 2022, 14, 2074. [Google Scholar] [CrossRef]
- Zhang, X. Application of Kinetic Methods in Thermal Analysis: A Review. Eng. Sci. 2021, 14, 1–13. [Google Scholar] [CrossRef]
- Friedman, H. Kinetics of thermal degradation of char-forming plastics from thermogravimetry. Application to a phenolic plastic. J. Polym. Sci. C Polym. Symp. 1964, 6, 183–195. [Google Scholar] [CrossRef]
- Šesták, J. Šesták–Berggren equation: Now questioned but formerly celebrated—what is right. J. Therm. Anal. Calorim. 2017, 127, 1117–1121. [Google Scholar] [CrossRef]
- Kamal, M. Thermoset characterization for moldability analysis. Polym. Eng. Sci. 1974, 14, 231–239. [Google Scholar] [CrossRef]
- Dluzneski, P. Peroxide vulcanization of elastomers. Rubber Chem. Technol. 2000, 74, 451–492. [Google Scholar] [CrossRef]
- Baquey, G.; Moine, L.; Babot, O.; Degueil, M.; Maillard, B. Model study of the crosslinking of polydimethylsiloxanes by peroxides. Polymer 2005, 46, 6283–6292. [Google Scholar]
- Wiśniewska, P.; Zedler, Ł.; Formela, K. Processing, Performance Properties, and Storage Stability of Ground Tire Rubber Modified by Dicumyl Peroxide and Ethylene-Vinyl Acetate Copolymers. Polymer 2021, 13, 4014. [Google Scholar] [CrossRef] [PubMed]
- Likozar, B.; Krajnc, M. Simulation of chemical kinetics of elastomer crosslinking by organic peroxides. Polym. Eng. Sci. 2009, 49, 60–72. [Google Scholar] [CrossRef]
- Kruželák, J.; Hakošová, S.; Kvasničáková, A.; Hudec, I. Dicumyl Peroxide used as curing Agent for different Typer of Rubber Matrices Part I: Effect of Temperature. KGK Kautsch. Gummi Kunststoffe 2020, 73, 36–42. [Google Scholar]
- Kruželák, J.; Hakošová, S.; Kvasničáková, A.; Hudec, I. Dicumyl Peroxide used as curing Agent for different Typer of Rubber Matrices Part II: Effect of peroxide Content. KGK Kautsch. Gummi Kunststoffe 2020, 73, 36–40. [Google Scholar]
- Duh, Y.S.; Kao, C.S.; Lee, W.L.W. Chemical kinetics on thermal decompositions of dicumyl peroxide studies by calorimetry. J. Therm. Anal. Calorim. 2017, 127, 1089–1098. [Google Scholar] [CrossRef]
- Lv, J.; Chen, L.; Chen, W.; Gao, H.; Peng, M. Kinetic analysis and self-accelerating decomposition temperature (SADT) of dicumyl peroxide. Thermochim. Acta 2013, 571, 60–63. [Google Scholar] [CrossRef]
- Hou, Q.; Yin, L.; Xu, L.; Tan, J. Effects of composite reinforcing filler, vulcanizing temperature, and pressure on mechanical properties of gasket material for proton exchange membrane fuel cells. J. Appl. Polym. Sci. 2022, 139, 52298. [Google Scholar] [CrossRef]
- Bianchi, O.; Martins, J.; Fiorio, R.; Oliveira, R.; Canto, L. Changes in activation energy and kinetic mechanism during EVA crosslinking. Polym. Test. 2011, 30, 616–624. [Google Scholar] [CrossRef]
- Granado, L.; Tavernier, R.; Foyer, G.; David, G.; Caillol, S. Comparative curing kinetics study of high char yield formaldehyde- and terephthalaldehyde-phenolic thermosets. Thermochim. Acta 2018, 667, 42–49. [Google Scholar] [CrossRef]
- Cheheb, Z.; Mousseau, P.; Sarda, A.; Deterre, R. Thermal Conductivity of Rubber Compounds Versus the State of Cure. Macromol. Mater. Eng. 2012, 297, 228–236. [Google Scholar] [CrossRef]
- Glasstone, S.; Laidler, K.; Eyring, H. The Theory of the Rate Processes; McGraw-Hill Book Co.: New York, NY, USA, 1941. [Google Scholar]
- Parks, C.; Lorenz, O. Crosslinking efficiency in the reaction of dicumyl peroxide with dimmethyloctadiene. J. Polym. Sci. 1961, 50, 287–298. [Google Scholar] [CrossRef]
- Hioe, J.; Zipse, H. Radical stability and its role in synthesis and catalysis. Org. Biomol. Chem. 2010, 8, 3609–3617. [Google Scholar] [CrossRef]
- Bordwell, F.; Zhang, X.M.; Alnakkar, S. Effects of Adjacent Acceptors and Donors on the Stabilities of Carbon-Centerd Radicals. J. Am. Chem. Soc. 1992, 447, 7623–7629. [Google Scholar] [CrossRef]
- Verheyen, F.; Giesen, R.U.; Heim, H.P. Mechanical Properties of Polydimethylsiloxane as a Function of the Amount and Type of Crosslinking Agent. Int. Polym. Process. 2017, 32, 337–342. [Google Scholar] [CrossRef]
- Soroceanu, A.; Stiubianu, G. Siloxane Matrix Molecular Weight Influences the Properties of Nanocomposites Based on Metal Complexes and Dielectric Elastomer. Materials 2021, 14, 3352. [Google Scholar] [CrossRef] [PubMed]
- Yokoyaza, T.; Yokoyama, A. Chain-Growth Polycondensation: Living Polymerization Nature in Polycondensation and Approach to Condensation Polymer Architecture. Polym. J. 2004, 36, 65–83. [Google Scholar] [CrossRef] [Green Version]
- Gao, X.; Hiu, H.; Wei, H.; Zheng, J.; Huang, G. Effect of incompletely condensed tri-silanol-phenyl-POSS on the thermal stability of silicone rubber. Polym. Bull. 2019, 76, 2835–2850. [Google Scholar] [CrossRef]
- Shi, S.; Lei, B.; Li, M.; Cui, X.; Wang, X.; Fan, X.; Tang, S.; Shen, J. Thermal decomposition behaviour of a thermal protection coating composite with silicone rubber: Experiment and modelling. Prog. Org. Coat. 2020, 143, 105609. [Google Scholar] [CrossRef]
- Saalwächter, K.; Reichert, D. Polymer Applications of NMR in Encyclopedia of Spectroscopy and Spectrometry, 3rd ed.; Elsevier Ltd.: Amsterdam, The Netherlands, 2017. [Google Scholar]






| Temperature | 140 C | 150 C | 160 C | 170 C | 180 C | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| (dN m) | (min) | (dN m) | (min) | (dN m) | (min) | (dN m) | (min) | (dN m) | (min) | |
| 0 phr | 0.58 | n/a | 0.57 | n/a | 0.56 | n/a | 0.54 | n/a | 0.41 | n/a |
| 0.21 phr | 0.61 | 19.98 | 0.60 | 6.16 | 0.58 | 2.12 | 0.56 | 0.96 | 0.53 | 0.53 |
| 0.35 phr | 0.62 | 11.13 | 0.62 | 3.63 | 0.58 | 1.29 | 0.55 | 0.64 | 0.55 | 0.39 |
| 0.49 phr | 0.60 | 9.40 | 0.59 | 3.02 | 0.57 | 1.16 | 0.55 | 0.58 | 0.54 | 0.36 |
| 0.70 phr | 0.61 | 8.06 | 0.60 | 2.63 | 0.58 | 1.01 | 0.56 | 0.53 | 0.54 | 0.35 |
| 1.00 phr | 0.61 | 3.76 | 0.58 | 1.31 | 0.56 | 0.63 | 0.55 | 0.57 | 0.56 | 0.28 |
| 1.50 phr | 0.58 | 2.62 | 0.56 | 1.05 | 0.53 | 0.57 | 0.57 | 0.37 | 0.53 | 0.28 |
| Temperature | 140 C | 150 C | 160 C | 170 C | 180 C | |||||
|---|---|---|---|---|---|---|---|---|---|---|
| (dN m) | (min) | (dN m) | (min) | (dN m) | (min) | (dN m) | (min) | (dN m) | (min) | |
| 0 phr | 0.72 | n/a | 0.77 | n/a | 0.91 | n/a | 1.07 | n/a | 1.28 | n/a |
| 0.21 phr | 7.76 | 45.45 | 9.89 | 20.92 | 10.48 | 8.91 | 11.25 | 4.54 | 11.54 | 2.92 |
| 0.35 phr | 8.72 | 31.15 | 10.26 | 12.94 | 10.86 | 5.43 | 11.57 | 2.99 | 11.76 | 1.64 |
| 0.49 phr | 8.93 | 27.07 | 9.97 | 10.18 | 10.87 | 4.72 | 11.57 | 2.44 | 11.64 | 1.25 |
| 0.70 phr | 9.4 | 24.37 | 9.95 | 8.93 | 10.98 | 4.21 | 11.57 | 2.13 | 11.82 | 1.19 |
| 1.00 phr | 11.40 | 16.74 | 11.92 | 8.75 | 12.39 | 4.5 | 12.56 | 2.93 | 12.63 | 1.22 |
| 1.50 phr | 11.05 | 12.58 | 11.55 | 6.97 | 11.78 | 4.14 | 12.07 | 4.53 | 12.06 | 1.04 |
| m | n | |||||||
|---|---|---|---|---|---|---|---|---|
| Sample | (min) | (min) | (kJ mol) | (kJ mol) | − | − | (min) | (min) |
| 0.21 phr | 131.35 | 131.35 | 1.167 | 1.617 | 0.1591 | 0.9261 | ||
| 0.25 phr | 127.47 | 127.47 | 1.298 | 1.621 | 0.2720 | 1.6150 | ||
| 0.49 phr | 125.75 | 125.75 | 1.210 | 1.552 | 0.3015 | 1.6444 | ||
| 0.70 phr | 123.92 | 123.92 | 1.350 | 1.667 | 0.3872 | 2.1638 | ||
| 1.00 phr | 87.67 | 87.60 | 2.048 | 2.760 | 0.8715 | 11.438 | ||
| 1.50 phr | 83.61 | 83.61 | 1.820 | 2.610 | 0.8269 | 9.0960 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Azevedo, M.; Monks, A.-M.; Kerschbaumer, R.C.; Schlögl, S.; Holzer, C. Peroxide-Based Crosslinking of Solid Silicone Rubber, Part I: Insights into the Influence of Dicumylperoxide Concentration on the Curing Kinetics and Thermodynamics Determined by a Rheological Approach. Polymers 2022, 14, 4404. https://doi.org/10.3390/polym14204404
Azevedo M, Monks A-M, Kerschbaumer RC, Schlögl S, Holzer C. Peroxide-Based Crosslinking of Solid Silicone Rubber, Part I: Insights into the Influence of Dicumylperoxide Concentration on the Curing Kinetics and Thermodynamics Determined by a Rheological Approach. Polymers. 2022; 14(20):4404. https://doi.org/10.3390/polym14204404
Chicago/Turabian StyleAzevedo, Maurício, Anna-Maria Monks, Roman C. Kerschbaumer, Sandra Schlögl, and Clemens Holzer. 2022. "Peroxide-Based Crosslinking of Solid Silicone Rubber, Part I: Insights into the Influence of Dicumylperoxide Concentration on the Curing Kinetics and Thermodynamics Determined by a Rheological Approach" Polymers 14, no. 20: 4404. https://doi.org/10.3390/polym14204404
APA StyleAzevedo, M., Monks, A. -M., Kerschbaumer, R. C., Schlögl, S., & Holzer, C. (2022). Peroxide-Based Crosslinking of Solid Silicone Rubber, Part I: Insights into the Influence of Dicumylperoxide Concentration on the Curing Kinetics and Thermodynamics Determined by a Rheological Approach. Polymers, 14(20), 4404. https://doi.org/10.3390/polym14204404