Melt Temperature Estimation by Machine Learning Model Based on Energy Flow in Injection Molding
Abstract
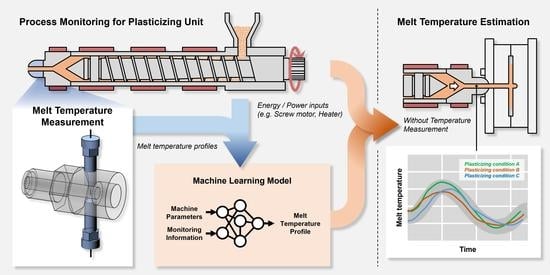
:1. Introduction
2. Method
3. Experiments
3.1. Materials and Instruments
3.2. Temperature Sensor
3.3. Energy Monitoring
- : internal energy change after the material is fed to the hopper before the melt is injected through the nozzle
- : energy transferred to the material by screw rotation
- : energy loss without being transmitted to the material, such as that from friction
- : energy supplied to the heaters in a cycle
- : heat energy loss by convection to the atmosphere and conduction to the machine
3.4. Experimental Conditions
3.5. Machine Learning Model
3.6. Transfer Learning Model
4. Results and Discussion
4.1. Melt Temperature Prediction
4.2. Improving Prediction Efficiency through Transfer Learning
4.3. Contributions of Features to Temperature Prediction
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Menges, G.; Michaeli, W.; Mohren, P. How to Make Injection Molds, 3rd ed.; Hanser Gardner Publications, Inc.: Cincinnati, OH, USA, 2000; pp. 543–551. [Google Scholar]
- Moldflow Insight; Autodesk, Inc.: San Rafael, CA, USA, 2021.
- Modex3D Studio; CoreTech System Co., Ltd.: Hsinchu, Taiwan, 2021.
- Amano, O.; Utsugi, S. Temperature measurements of polymer melts in the heating barrel during injection molding. Part I. Temperature distribution along the screw axis in the reservoir. Polym. Eng. Sci. 1988, 28, 1565–1571. [Google Scholar] [CrossRef]
- Amano, O.; Utsugi, S. Temperature measurements of polymer melts in the heating barrel during injection molding. Part 2: Three-dimensional temperature distribution in the reservoir. Polym. Eng. Sci. 1989, 29, 171–177. [Google Scholar] [CrossRef]
- Isayev, A.; Hosaki, T. Temperature in Rubber Moldings during Injection Molding Cycle: Simulation and Experimentation. J. Elastomers Plast. 1991, 23, 176–191. [Google Scholar] [CrossRef]
- Jeon, J.H.; Gim, J.S.; Rhee, B.O. The Melt Temperature Variation in the Barrel of Injection Molding Machine. In Proceedings of the Society of Plastics Engineers Annual Technical Conference (SPE ANTEC), Indianapolis, IN, USA, 23–25 May 2016. [Google Scholar]
- Straka, K.; Praher, B.; Steinbichler, G. Analyzing melt homogeneity in a single screw plasticizing unit of an injection molding machine. In Proceedings of the 12th International Conference of Numerical Analysis and Applied Mathematics, Rhodes, Greece, 21–27 September 2013. [Google Scholar]
- Gim, J.; Turng, L.-S. A review of current advancements in high surface quality injection molding: Measurement, influencing factors, prediction, and control. Polym. Test. 2022, 115, 107718. [Google Scholar] [CrossRef]
- Zhou, Y.; Mallick, P. Effects of melt temperature and hold pressure on the tensile and fatigue properties of an injection molded talc-filled polypropylene. Polym. Eng. Sci. 2005, 45, 755–763. [Google Scholar] [CrossRef]
- Wu, C.-H.; Liang, W.-J. Effects of geometry and injection-molding parameters on weld-line strength. Polym. Eng. Sci. 2005, 45, 1021–1030. [Google Scholar] [CrossRef]
- Kamal, M.R.; Varela, A.E.; Patterson, W.I. Control of part weight in injection molding of amorphous thermoplastics. Polym. Eng. Sci. 1999, 39, 940–952. [Google Scholar] [CrossRef]
- Dubay, R.; Bell, A.C.; Gupta, Y.P. Control of plastic melt temperature: A multiple input multiple output model predictive approach. Polym. Eng. Sci. 1997, 37, 1559–1563. [Google Scholar] [CrossRef]
- Nunn, R.E.; Fenner, R.T. Flow and heat transfer in the nozzle of an injection molding machine. Polym. Eng. Sci. 1977, 17, 811–818. [Google Scholar] [CrossRef]
- Sombatsompop, N.; Chaiwattanpipat, W. Temperature profiles of glass fibre-filled polypropylene melts in injection moulding. Polym. Test. 2000, 19, 713–724. [Google Scholar] [CrossRef]
- Debey, D.; Bluhm, R.; Habets, N.; Kurz, H. Fabrication of planar thermocouples for real-time measurements of temperature profiles in polymer melts. Sens. Actuators A Phys. 1997, 58, 179–184. [Google Scholar] [CrossRef]
- Dontula, N.; Sukanek, P.C.; Devanathan, H.; Campbell, G.A. An experimental and theoretical investigation of transient melt temperature during injection molding. Polym. Eng. Sci. 1991, 31, 1674–1683. [Google Scholar] [CrossRef]
- Praher, B.; Straka, K.; Steinbichler, G. An ultrasound-based system for temperature distribution measurements in injection moulding: System design, simulations and off-line test measurements in water. Meas. Sci. Technol. 2013, 24, 084004. [Google Scholar] [CrossRef]
- Kim, J.G.; Kim, H.; Kim, H.S.; Lee, J.W. Investigation of pressure-volume-temperature relationship by ultrasonic technique and its application for the quality prediction of injection molded parts. Korea Aust. Polym. Eng. Sci. Rheol. J. 2004, 16, 163–168. [Google Scholar]
- Kamal, M.R.; Kenig, S. The injection molding of thermoplastics part I: Theoretical model. Polym. Eng. Sci. 1972, 12, 294–301. [Google Scholar] [CrossRef]
- Zhao, C.; Gao, F. Melt temperature profile prediction for thermoplastic injection molding. Polym. Eng. Sci. 1999, 39, 1787–1801. [Google Scholar] [CrossRef]
- Lee, C.; Na, J.; Park, K.; Yu, H.; Kim, J.; Choi, K.; Park, D.; Park, S.; Rho, J.; Lee, S. Development of artificial neural network system to recommend process conditions of injection molding for various geometries. Adv. Intell. Syst. 2020, 2, 2000037. [Google Scholar] [CrossRef]
- Tercan, H.; Guajardo, A.; Heinisch, J.; Thiele, T.; Hopmann, C.; Meisen, T. Transfer-Learning: Bridging the Gap between Real and Simulation Data for Machine Learning in Injection Molding. In Proceedings of the 51st CIRP Conference on Manufacturing Systems (CIRP CMS 2018), Stockholm, Sweden, 16–18 May 2018. [Google Scholar]
- Gim, J.; Rhee, B. Novel Analysis Methodology of Cavity Pressure Profiles in Injection-Molding Processes Using Interpretation of Machine Learning Model. Polymers 2021, 13, 3297. [Google Scholar] [CrossRef]
- Gedeon, T.D. Data mining of inputs: Analysing magnitude and functional measures. Int. J. Neural Syst. 1997, 8, 209–218. [Google Scholar] [CrossRef]
- Bradley, D.; Matthews, K.J. Measurement of high gas temperatures with fine wire thermocouples. J. Mech. Eng. Sci. 1968, 10, 299–305. [Google Scholar] [CrossRef]
- Akiba, T.; Sano, S.; Yanase, T.; Ohta, T.; Koyama, M. Optuna: A Next-generation Hyperparameter Optimization Framework. In Proceedings of the 25th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, New York, NY, USA, 4–8 August 2019. [Google Scholar]
- Pan, S.J.; Yang, Q. A Survey on Transfer Learning. IEEE Trans. Knowl. Data Eng. 2010, 22, 1345–1359. [Google Scholar] [CrossRef]
- Torrey, L.; Shavlik, J. Transfer Learning. In Handbook of Research on Machine Learning Applications and Trends: Algorithms, Methods, and Techniques; IGI Global: Hershey, PA, USA, 2010; pp. 242–264. [Google Scholar]
- Yosinski, J.; Clune, J.; Bengio, Y.; Lipson, H. How transferable are features in deep neural networks? Adv. Neural Inf. Process. Syst. 2014, 27, 3320–3328. [Google Scholar]
- Lockner, Y.; Hopmann, C.; Zhao, W. Transfer learning with artificial neural networks between injection molding processes and different polymer materials. J. Manuf. Process. 2022, 73, 395–408. [Google Scholar] [CrossRef]
- Lundberg, S.M.; Erion, G.; Chen, H.; DeGrave, A.; Prutkin, J.M.; Nair, B.; Katz, R.; Himmelfarb, J.; Bansal, N.; Lee, S.I.; et al. From local explanations to global understanding with explainable AI for trees. Nat. Mach. Intell. 2020, 2, 56–67. [Google Scholar] [CrossRef]














| Factor | Level | ||
|---|---|---|---|
| 1 | 2 | 3 | |
| Screw rotation speed (RPM) | 50 | 175 | 300 |
| Backpressure (bar) | 20 | 100 | 400 |
| Heater temperature (°C) | 200 | 240 | - |
| Heater profile | Flat | Decrease | - |
| Forced cooling | 0 | 1 | - |
| Dwell time (s) | 0 | 20 | 60 |
| Factor | Level | |
|---|---|---|
| 1 | 2 | |
| Screw rotation speed (RPM) | 50 | 300 |
| Backpressure (bar) | 20 | 400 |
| Heater temperature (°C) | 200 | 240 |
| Heater profile | Flat | Decrease |
| Forced cooling | 0 | 1 |
| Dwell time (s) | 0 | 60 |
| Parameter | Value |
|---|---|
| Number of hidden layers | 4 |
| Number of input layer neurons | 16 |
| Number of hidden layer neurons | 150 |
| Number of output layer neurons | 100 |
| Hidden layer activation function | ReLU |
| Optimizer | Adamax |
| Loss function | RMSE |
| Training iterations (epochs) | 1000 |
| Model | Input Features |
|---|---|
| Model 1 (conventional; process setting parameters only) | Screw rotation speed, back pressure, feed stroke, barrel heater temperatures, dwell time |
| Model 2 (model 1 + monitoring data) | Energy consumption of each heater, energy consumption of plasticizing motor (screw rotation), cycle time, ambient temperature |
| Model 3 (model 2 + material data) | Specific heat of material, product weights |
| Parameter | Value |
|---|---|
| Number of non-trainable (frozen) layers | 3 (input layer side) |
| Number of trainable layers | 2 (1 existing layer, 1 additional layer) |
| Amount of data used for training (%) | 10, 20, 30, 40, 50, 60, 70, 80, 90 |
| Model | RMSE | R2 |
|---|---|---|
| Model 1 (conventional; process setting parameters only) | 0.2468 | 0.926 |
| Model 2 (model 1 + monitoring data) | 0.1704 | 0.950 |
| Model 3 (full data; model 2 + material data) | 0.0647 | 0.971 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jeon, J.; Rhee, B.; Gim, J. Melt Temperature Estimation by Machine Learning Model Based on Energy Flow in Injection Molding. Polymers 2022, 14, 5548. https://doi.org/10.3390/polym14245548
Jeon J, Rhee B, Gim J. Melt Temperature Estimation by Machine Learning Model Based on Energy Flow in Injection Molding. Polymers. 2022; 14(24):5548. https://doi.org/10.3390/polym14245548
Chicago/Turabian StyleJeon, Joohyeong, Byungohk Rhee, and Jinsu Gim. 2022. "Melt Temperature Estimation by Machine Learning Model Based on Energy Flow in Injection Molding" Polymers 14, no. 24: 5548. https://doi.org/10.3390/polym14245548
APA StyleJeon, J., Rhee, B., & Gim, J. (2022). Melt Temperature Estimation by Machine Learning Model Based on Energy Flow in Injection Molding. Polymers, 14(24), 5548. https://doi.org/10.3390/polym14245548