Consideration of Yarn Anisotropy in the Investigation of the Puncture Resistance of Fibrous Materials
Abstract
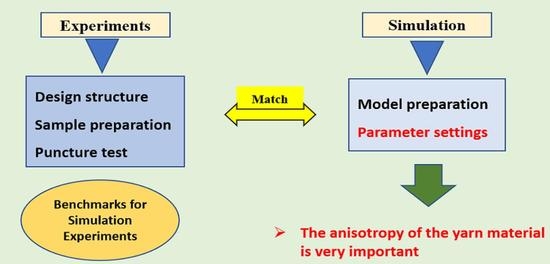
:1. Introduction
2. Puncture Experiment
2.1. Experiment Preparation
2.2. Determination of Material Parameters
2.2.1. Measurement of Axial Modulus
2.2.2. Measurement of Radial Modulus
- U: the change in fiber diameter;
- F: the compressive force;
- ET: the transverse modulus of the fiber;
- LT: the longitudinal Poisson’s ratio of the fiber;
- R: the radius of the fiber; and
- b: the contact width of the fiber during compression.
- ET: the transverse modulus of the fiber;
- F: the compressive force;
- R: the radius of the fiber;
- L: the length of the fiber during compression; and
- : the strain of the fiber.
2.3. Puncture Experiments
2.4. Dynamic Analysis of the Puncture Results
3. Simulation Experiment
3.1. Model Establishment
- (1)
- the yarns were continuous filaments with uniform bars, and the cross section was a runway type; and
- (2)
- the composite material had no defects and the resin distribution was uniform [28].
3.2. Model Parameters
3.3. Puncture Simulation
3.3.1. Comparison of Simulation Results
3.3.2. Microscopic Analysis of the Simulated Puncture Results
- (1)
- Stress analysis of the whole fabric
- (2)
- Stress analysis of central yarns
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Nayak, R.; Crouch, I.; Kanesalingam, S.; Ding, J.; Tan, P.; Lee, B.; Miao, M.; Ganga, D.; Wang, L. Body armor for stab and spike protection, Part 1: Scientific literature review. Text. Res. J. 2018, 88, 812–832. [Google Scholar] [CrossRef]
- Horsfall, I. Stab Resistant Body Armour. Ph.D. Thesis, Engineering Systems Department, College of Defense Technology, Cranfield University, Cranfield, UK, 2000. [Google Scholar]
- Zheng, L.; Zhang, K.; Liu, L.; Xu, F. Biomimetic architectured Kevlar/polyimide composites with ultra-light, superior anti-compressive and flame-retardant properties. Compos. Part B Eng. 2022, 230, 109485. [Google Scholar] [CrossRef]
- Zhou, J.; Zhang, J.; Sang, M.; Liu, S.; Yuan, F.; Wang, S.; Sun, S.; Gong, X. Advanced functional Kevlar composite with excellent mechanical properties for thermal management and intelligent safeguarding. Chem. Eng. J. 2022, 428, 131878. [Google Scholar] [CrossRef]
- Usman Javaid, M.; Militký, J.; Wiener, J.; Jabbar, A.; Salačová, J.; Umair, M. Effect of surface modification and knife penetration angle on the quasi-static knife penetration resistance of para-aramid fabrics. J. Text. Inst. 2019, 110, 590–599. [Google Scholar] [CrossRef]
- Zhang, J.; Wang, Y.; Zhou, J.; Zhao, C.; Wu, Y.; Liu, S.; Gong, X. Intralayer interfacial sliding effect on the anti-impact performance of STF/Kevlar composite fabric. Compos. Part A Appl. Sci. Manuf. 2021, 145, 106401. [Google Scholar] [CrossRef]
- Sy, B.L.; Oguamanam, D.; Bougherara, H. Impact response of a new kevlar/flax/epoxy hybrid composite using infrared thermography and high-speed imaging. Compos. Struct. 2022, 280, 114885. [Google Scholar]
- Eltaher, M.A.; Basha, M.; Wagih, A.; Melaibari, A.; Lubineau, G. On the impact damage resistance and tolerance improvement of hybrid CFRP/Kevlar sandwich composites. Microporous Mesoporous Mater. 2022, 333, 111732. [Google Scholar]
- White, Z.; Vernerey, F. Armours for soft bodies: How far can bioinspiration take us? Bioinspir. Biomim. 2018, 13, 041004. [Google Scholar] [CrossRef] [Green Version]
- Guleria, T.; Verma, N.; Zafar, S.; Jain, V. Fabrication of Kevlar-reinforced ultra-high molecular weight polyethylene composite through microwave-assisted compression molding for body armor applications. J. Reinf. Plast. Compos. 2021, 40, 307–320. [Google Scholar] [CrossRef]
- Karamooz, M.R.; Rahmani, H.; Khosravi, H. Numerical and experimental investigations on the low-velocity impact properties of hybrid Kevlar fiber/basalt fiber reinforced epoxy composites: Effects of impactor nose shape and fiber stacking sequences. Polym. Compos. 2021, 42, 6442–6454. [Google Scholar] [CrossRef]
- Hetrick, D.R.; Sanei, S.H.R.; Ashour, O.; Bakis, C.E. Charpy impact energy absorption of 3D printed continuous Kevlar reinforced composites. J. Compos. Mater. 2021, 55, 1705–1713. [Google Scholar] [CrossRef]
- Hou, X.; Acar, M.; Silberschmidt, V.V. 2D finite element analysis of thermally bonded nonwoven materials: Continuous and discontinuous models. Comput. Mater. Sci. 2009, 46, 700–707. [Google Scholar] [CrossRef] [Green Version]
- Ridruejo, A.; González, C.; LLorcaab, J. Damage micromechanisms and notch sensitivity of glass-fiber non-woven felts: An experimental and numerical study. J. Mech. Phys. Solids 2010, 58, 1628–1645. [Google Scholar] [CrossRef]
- Zeng, J.; Cao, H.; Hu, H. Finite element simulation of an auxetic plied yarn structure. Text. Res. J. 2018, 89, 3394–3400. [Google Scholar] [CrossRef]
- Zhou, H.; Xiao, X.; Qian, K.; Ma, Q. Numerical simulation and experimental study of the bursting performance of triaxial woven fabric and its reinforced rubber composites. Text. Res. J. 2019, 90, 561–571. [Google Scholar] [CrossRef]
- Sun, B.; Wang, Y.; Wang, P.; Hu, H.; Gu, B. Investigations of puncture behaviors of woven fabrics from finite element analyses and experimental tests. Text. Res. J. 2011, 81, 992–1007. [Google Scholar] [CrossRef]
- Zhu, D.; Szewciw, L.; Vernerey, F.; Barthelat, F. Puncture resistance of the scaled skin from striped bass: Collective mechanisms and inspiration for new flexible armor designs. J. Mech. Behav. Biomed. Mater. 2013, 24, 30–40. [Google Scholar] [CrossRef]
- Lian, J.; Bohong, G.U. Numerical simulation of dynamic performance of three-dimensional braided composites. J. Text. Res. 2011, 32, 41–45. [Google Scholar]
- Termonia, Y. Puncture resistance of fibrous structures. Int. J. Impact Eng. 2006, 32, 1512–1520. [Google Scholar] [CrossRef]
- Bao, L.; Wang, Y.; Baba, T.; Fukuda, Y.; Wakatsuki, K.; Morikawa, H. Development of a high-density nonwoven structure to improve the stab resistance of protective clothing material. Ind. Health 2017, 55, 513–520. [Google Scholar] [CrossRef] [Green Version]
- Bao, L.; Sato, S.; Wang, Y.; Wakatsuki, K.; Morikawa, H. Development of flexible stab-proof textiles impregnated with microscopic particles. J. Text. Eng. 2017, 63, 43–48. [Google Scholar] [CrossRef]
- Chuang, Y.-C.; Bao, L.; Lin, M.C.; Lou, C.W.; Lin, T. Mechanical and static stab resistant properties of hybrid-fabric fibrous planks: Manufacturing process of nonwoven fabrics made of recycled fibers. Polymers 2019, 11, 1140. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Carrillo, J.G.; Castellanos, R.G.; Flores-Johnson, E.A.; Gonzalez-Chi, P.I. Ballistic performance of thermoplastic composite laminates made from aramid woven fabric and polypropylene matrix. Polym. Test. 2012, 31, 512–519. [Google Scholar] [CrossRef] [Green Version]
- Kawabata, S. Measurement of the transverse mechanical properties of high-performance fibres. J. Text. Inst. 1990, 81, 432–447. [Google Scholar] [CrossRef]
- Ruan, F.; Bao, L. Mechanical enhancement of UHMWPE fibers by coating with carbon nanoparticles. Fibers Polym. 2014, 15, 723–728. [Google Scholar] [CrossRef] [Green Version]
- Bao, L.; Sato, S.; Morioka, H.; Soma, S. Improving stab-resistant textile materials with a non-woven fabric structure. J. Text. Eng. 2016, 62, 37–42. [Google Scholar] [CrossRef] [Green Version]
- Ju, W.; Dai, W.W. Application of ANSYS Workbench in structural transient dynamic analysis. Inner Mong. Coal Econ. 2014, 8, 110–113. [Google Scholar]
- Stolarski, T.; Nakasone, Y.; Yoshimoto, S. Engineering Analysis with ANSYS Software; Butterworth-Heinemann: Oxford, UK, 2018. [Google Scholar]
- Zhu, L.; Liu, W.; Fang, H.; Qian, Z.; ZHUANG, Y. Experiment and finite element analysis of lattice reinforced composite sandwich panels subjected to low-velocity impact. J. Nanjing Univ. Technol. Nat. Sci. Ed. 2017, 39, 126–132. [Google Scholar]
- Gzaiel, M.; Triki, E.; Barkaoui, A. Finite element modeling of the puncture-cutting response of soft material by a pointed blade. Mech. Mater. 2019, 136, 103082. [Google Scholar] [CrossRef]
- Luo, C.; Cao, H.; Huang, X. Numerical simulation on low velocity impact response of three-dimensional sandwich composites with different core height. Text. Res. J. 2019, 40, 48–54. [Google Scholar]

















| Young’s Modulus (GPa) | Tensile/Compression Strength (GPa) | Failure Strain | |
|---|---|---|---|
| Axial direction of yarn | 78.62 ± 2.54 | 2.58 ± 0.32 | 0.032 ± 0.0024 |
| Radial direction of yarn | 0.32 ± 0.04 | 0.23 ± 0.02 | 0.263 ± 0.031 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Luo, C.; Sun, Y.; Wakatsuki, K.; Morikawa, H.; Bao, L. Consideration of Yarn Anisotropy in the Investigation of the Puncture Resistance of Fibrous Materials. Polymers 2022, 14, 883. https://doi.org/10.3390/polym14050883
Luo C, Sun Y, Wakatsuki K, Morikawa H, Bao L. Consideration of Yarn Anisotropy in the Investigation of the Puncture Resistance of Fibrous Materials. Polymers. 2022; 14(5):883. https://doi.org/10.3390/polym14050883
Chicago/Turabian StyleLuo, Chao, Ye Sun, Kaoru Wakatsuki, Hideaki Morikawa, and Limin Bao. 2022. "Consideration of Yarn Anisotropy in the Investigation of the Puncture Resistance of Fibrous Materials" Polymers 14, no. 5: 883. https://doi.org/10.3390/polym14050883
APA StyleLuo, C., Sun, Y., Wakatsuki, K., Morikawa, H., & Bao, L. (2022). Consideration of Yarn Anisotropy in the Investigation of the Puncture Resistance of Fibrous Materials. Polymers, 14(5), 883. https://doi.org/10.3390/polym14050883