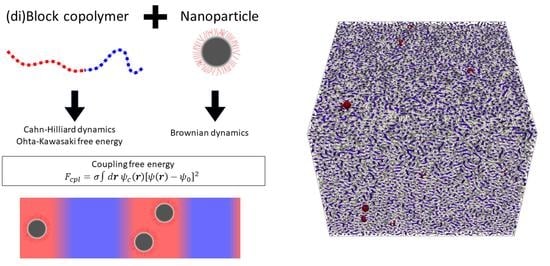
Hybrid Time-Dependent Ginzburg–Landau Simulations of Block Copolymer Nanocomposites: Nanoparticle Anisotropy
Abstract
:1. Introduction
Complex Anisotropic NPs within BCP
2. Time-Dependent Ginzburg–Landau Coupled with Brownian Dynamics
2.1. Block Copolymer Dynamics: Time-Dependent Ginzburg–Landau
2.2. Numerical Scheme: Cell Dynamic Simulations
2.3. Coupling BCP Field and NPs
2.4. Colloidal Dynamics: Brownian Motion
2.5. Anisotropic Colloids: Nonspherical Particles
2.6. Anisotropic Potentials
2.7. Anisotropic Colloids: Chemically Inhomogeneous Coatings
2.8. Extension for Dynamics of Orientational Degrees of Freedom
2.9. Parallelisation
3. Applications of Hybrid TDGL/BD Models
3.1. Mixtures of BCP and Isotropic NPs
3.2. Three-Dimensional Systems
3.3. Shape-Anisotropic NPs
3.4. Chemically Inhomogeneous NPs
4. Concluding Remarks
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Kumar, S.K.; Krishnamoorti, R. Nanocomposites: Structure, Phase Behavior, and Properties. Annu. Rev. Chem. Biomol. Eng. 2010, 1, 37–58. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Caseri, W. Nanocomposites of polymers and metals or semiconductors: Historical background and optical properties. Macromol. Rapid Commun. 2000, 21, 705–722. [Google Scholar] [CrossRef]
- Vaia, R.A.; Giannelis, E.P. Polymer Nanocomposites: Status and Opportunities. MRS Bull. 2001, 26, 394–401. [Google Scholar] [CrossRef]
- Vaia, R.A.; Maguire, J.F. Polymer nanocomposites with prescribed morphology: Going beyond nanoparticle-filled polymers. Chem. Mater. 2007, 19, 2736–2751. [Google Scholar] [CrossRef]
- Hore, M.J.A.; Composto, R.J. Functional Polymer Nanocomposites Enhanced by Nanorods. Macromolecules 2014, 47, 875–887. [Google Scholar] [CrossRef]
- Sarkar, B.; Alexandridis, P. Block copolymer–nanoparticle composites: Structure, functional properties, and processing. Prog. Polym. Sci. 2015, 40, 33–62. [Google Scholar] [CrossRef]
- Xie, X.L.; Mai, Y.W.; Zhou, X.P. Dispersion and alignment of carbon nanotubes in polymer matrix: A review. Mater. Sci. Eng. R Rep. 2005, 49, 89–112. [Google Scholar] [CrossRef]
- Förster, S.; Plantenberg, T. From Self-Organizing Polymers to Nanohybrid and Biomaterials. Angew. Chem. Int. Ed. 2002, 41, 688–714. [Google Scholar] [CrossRef]
- Smart, T.; Lomas, H.; Massignani, M.; Flores-Merino, M.V.; Perez, L.R.; Battaglia, G. Block copolymer nanostructures. Nano Today 2008, 3, 38–46. [Google Scholar] [CrossRef]
- Bockstaller, M.R.; Mickiewicz, R.A.; Thomas, E.L. Block Copolymer Nanocomposites: Perspectives for Tailored Functional Materials. Adv. Mater. 2005, 17, 1331–1349. [Google Scholar] [CrossRef]
- Zhao, Y.; Thorkelsson, K.; Mastroianni, A.J.; Schilling, T.; Luther, J.M.; Rancatore, B.J.; Matsunaga, K.; Jinnai, H.; Wu, Y.; Poulsen, D.; et al. Small-molecule-directed nanoparticle assembly towards stimuli-responsive nanocomposites. Nat. Mater. 2009, 8, 979–985. [Google Scholar] [CrossRef]
- Botti, A.; Pyckhout-Hintzen, W.; Richter, D.; Urban, V.; Straube, E. A microscopic look at the reinforcement of silica-filled rubbers. J. Chem. Phys. 2006, 124, 174908. [Google Scholar] [CrossRef] [Green Version]
- Chodák, I.; Omastová, M.; Pionteck, J. Relation between electrical and mechanical properties of conducting polymer composites. J. Appl. Polym. Sci. 2001, 82, 1903–1906. [Google Scholar] [CrossRef]
- Liedel, C.; Schindler, K.A.; Pavan, M.J.; Lewin, C.; Pester, C.W.; Ruppel, M.; Urban, V.S.; Shenhar, R.; Böker, A. Electric-Field-Induced Alignment of Block Copolymer/Nanoparticle Blends. Small 2013, 9, 3276–3281. [Google Scholar] [CrossRef] [PubMed]
- Morgan, A.B.; Wilkie, C.A. Flame Retardant Polymer Nanocomposites; John Wiley & Sons: Hoboken, NJ, USA, 2007. [Google Scholar]
- Templin, M.; Franck, A.; Du Chesne, A.; Leist, H.; Zhang, Y.; Ulrich, R.; Schädler, V.; Wiesner, U. Organically Modified Aluminosilicate Mesostructures from Block Copolymer Phases. Science 1997, 278, 1795–1798. [Google Scholar] [CrossRef] [PubMed]
- Zhao, D. Triblock Copolymer Syntheses of Mesoporous Silica with Periodic 50 to 300 Angstrom Pores. Science 1998, 279, 548–552. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Chan, V.Z. Ordered Bicontinuous Nanoporous and Nanorelief Ceramic Films from Self Assembling Polymer Precursors. Science 1999, 286, 1716–1719. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Yoon, J.; Lee, W.; Thomas, E.L. Self-Assembly of Block Copolymers for Photonic-Bandgap Materials. MRS Bull. 2005, 30, 721–726. [Google Scholar] [CrossRef] [Green Version]
- Ganesan, V.; Jayaraman, A. Theory and simulation studies of effective interactions, phase behavior and morphology in polymer nanocomposites. Soft Matter 2014, 10, 13–38. [Google Scholar] [CrossRef]
- Bates, F.S.; Fredrickson, G.H. Block Copolymer Thermodynamics: Theory and Experiment. Annu. Rev. Phys. Chem. 1990, 41, 525–557. [Google Scholar] [CrossRef]
- Zvelindovsky, A.V. (Ed.) Nanostructured Soft Matter: Experiments, Theory, Numerical Simulations and Perspectives; NanoScience and Technology, Springer: Dordrecht, The Netherlands, 2007. [Google Scholar]
- Segalman, R.A. Patterning with block copolymer thin films. Mater. Sci. Eng. R Rep. 2005, 48, 191–226. [Google Scholar] [CrossRef] [Green Version]
- Stoykovich, M.P.; Müller, M.; Kim, S.O.; Solak, H.H.; Edwards, E.W.; de Pablo, J.J.; Nealey, P.F. Directed Assembly of Block Copolymer Blends into Nonregular Device-Oriented Structures. Science 2005, 308, 1442–1446. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Freer, E.M.; Krupp, L.E.; Hinsberg, W.D.; Rice, P.M.; Hedrick, J.L.; Cha, J.N.; Miller, R.D.; Kim, H.C. Oriented Mesoporous Organosilicate Thin Films. Nano Lett. 2005, 5, 2014–2018. [Google Scholar] [CrossRef] [PubMed]
- Vavasour, J.D.; Whitmore, M.D. Self-consistent mean field theory of the microphases of diblock copolymers. Macromolecules 1992, 25, 5477–5486. [Google Scholar] [CrossRef]
- Matsen, M.W.; Schick, M. Stable and unstable phases of a diblock copolymer melt. Phys. Rev. Lett. 1994, 72, 2660–2663. [Google Scholar] [CrossRef]
- Matsen, M.W.; Bates, F.S. Unifying Weak- and Strong-Segregation Block Copolymer Theories. Macromolecules 1996, 29, 1091–1098. [Google Scholar] [CrossRef]
- Nonomura, M.; Yamada, K.; Ohta, T. Formation and stability of double gyroid in microphase-separated diblock copolymers. J. Phys. Condens. Matter 2003, 15, L423–L430. [Google Scholar] [CrossRef]
- Hamley, I.W. The Physics of Block Copolymers; Oxford University Press: Oxford, NY, USA, 1998. [Google Scholar]
- Park, C.; Yoon, J.; Thomas, E.L. Enabling nanotechnology with self assembled block copolymer patterns. Polymer 2003, 44, 6725–6760. [Google Scholar] [CrossRef] [Green Version]
- Cohen, R.E. Block copolymers as templates for functional materials. Curr. Opin. Solid State Mater. Sci. 1999, 4, 587–590. [Google Scholar] [CrossRef]
- Haryono, A.; Binder, W. Controlled Arrangement of Nanoparticle Arrays in Block-Copolymer Domains. Small 2006, 2, 600–611. [Google Scholar] [CrossRef]
- Li, Q.; He, J.; Glogowski, E.; Li, X.; Wang, J.; Emrick, T.; Russell, T.P. Responsive Assemblies: Gold Nanoparticles with Mixed Ligands in Microphase Separated Block Copolymers. Adv. Mater. 2008, 20, 1462–1466. [Google Scholar] [CrossRef]
- Kim, B.J.; Bang, J.; Hawker, C.J.; Chiu, J.J.; Pine, D.J.; Jang, S.G.; Yang, S.M.; Kramer, E.J. Creating Surfactant Nanoparticles for Block Copolymer Composites through Surface Chemistry. Langmuir 2007, 23, 12693–12703. [Google Scholar] [CrossRef] [PubMed]
- Kim, B.J.; Bang, J.; Hawker, C.J.; Kramer, E.J. Effect of Areal Chain Density on the Location of Polymer-Modified Gold Nanoparticles in a Block Copolymer Template. Macromolecules 2006, 39, 4108–4114. [Google Scholar] [CrossRef]
- Kim, B.J.; Fredrickson, G.H.; Kramer, E.J. Effect of Polymer Ligand Molecular Weight on Polymer-Coated Nanoparticle Location in Block Copolymers. Macromolecules 2008, 41, 436–447. [Google Scholar] [CrossRef]
- Spontak, R.J.; Shankar, R.; Bowman, M.K.; Krishnan, A.S.; Hamersky, M.W.; Samseth, J.; Bockstaller, M.R.; Rasmussen, K.ø. Selectivity- and Size-Induced Segregation of Molecular and Nanoscale Species in Microphase-Ordered Triblock Copolymers. Nano Lett. 2006, 6, 2115–2120. [Google Scholar] [CrossRef]
- Michman, E.; Shenhar, R. Directed self-assembly of block copolymer-based nanocomposites in thin films: Directed Self-Assembly of Block Copolymer-Based Nanocomposites. Polym. Adv. Technol. 2017, 28, 613–622. [Google Scholar] [CrossRef]
- Chiu, J.J.; Kim, B.J.; Kramer, E.J.; Pine, D.J. Control of Nanoparticle Location in Block Copolymers. J. Am. Chem. Soc. 2005, 127, 5036–5037. [Google Scholar] [CrossRef] [Green Version]
- Chiu, J.J.; Kim, B.J.; Yi, G.R.; Bang, J.; Kramer, E.J.; Pine, D.J. Distribution of Nanoparticles in Lamellar Domains of Block Copolymers. Macromolecules 2007, 40, 3361–3365. [Google Scholar] [CrossRef]
- Horechyy, A.; Nandan, B.; Zafeiropoulos, N.E.; Jehnichen, D.; Göbel, M.; Stamm, M.; Pospiech, D. Nanoparticle directed domain orientation in thin films of asymmetric block copolymers. Colloid Polym. Sci. 2014, 292, 2249–2260. [Google Scholar] [CrossRef]
- Ploshnik, E.; Langner, K.M.; Halevi, A.; Ben-Lulu, M.; Müller, A.H.E.; Fraaije, J.G.E.M.; Agur Sevink, G.J.; Shenhar, R. Hierarchical Structuring in Block Copolymer Nanocomposites through Two Phase-Separation Processes Operating on Different Time Scales. Adv. Funct. Mater. 2013, 23, 4215–4226. [Google Scholar] [CrossRef]
- Leffler, V.B.; Ehlert, S.; Förster, B.; Dulle, M.; Förster, S. 3D-Positioning of Nanoparticles in High-Curvature Block Copolymer Domains. Angew. Chem. Int. Ed. 2021, 60, 17539–17546. [Google Scholar] [CrossRef] [PubMed]
- Horechyy, A.; Paturej, J.; Nandan, B.; Jehnichen, D.; Göbel, M.; Reuter, U.; Sommer, J.U.; Stamm, M. Nanoparticle assembly under block copolymer confinement: The effect of nanoparticle size and confinement strength. J. Colloid Interface Sci. 2020, 578, 441–451. [Google Scholar] [CrossRef] [PubMed]
- Nam, T.W.; Jeong, J.W.; Choi, M.J.; Baek, K.M.; Kim, J.M.; Hur, Y.H.; Kim, Y.; Jung, Y.S. Single Nanoparticle Localization in the Perforated Lamellar Phase of Self-Assembled Block Copolymer Driven by Entropy Minimization. Macromolecules 2015, 48, 7938–7944. [Google Scholar] [CrossRef]
- Leffler, V.B.; Mayr, L.; Paciok, P.; Du, H.; Dunin-Borkowski, R.E.; Dulle, M.; Förster, S. Controlled Assembly of Block Copolymer Coated Nanoparticles in 2D Arrays. Angew. Chem. Int. Ed. 2019, 58, 8541–8545. [Google Scholar] [CrossRef] [PubMed]
- Yoo, M.; Kim, S.; Jang, S.G.; Choi, S.H.; Yang, H.; Kramer, E.J.; Lee, W.B.; Kim, B.J.; Bang, J. Controlling the orientation of block copolymer thin films using thermally-stable gold nanoparticles with tuned surface chemistry. Macromolecules 2011, 44, 9356–9365. [Google Scholar] [CrossRef]
- Chervanyov, A. Conductivity of diblock copolymer system filled with conducting nano-particles: Effect of copolymer morphology. J. Polym. Sci. 2022, 60, 221–232. [Google Scholar] [CrossRef]
- Huh, J.; Ginzburg, V.V.; Balazs, A.C. Thermodynamic Behavior of Particle/Diblock Copolymer Mixtures: Simulation and Theory. Macromolecules 2000, 33, 8085–8096. [Google Scholar] [CrossRef]
- Kim, B.J.; Chiu, J.J.; Yi, G.R.; Pine, D.J.; Kramer, E.J. Nanoparticle-Induced Phase Transitions in Diblock-Copolymer Films. Adv. Mater. 2005, 17, 2618–2622. [Google Scholar] [CrossRef]
- Lo, C.T.; Lee, B.; Pol, V.G.; Dietz Rago, N.L.; Seifert, S.; Winans, R.E.; Thiyagarajan, P. Effect of Molecular Properties of Block Copolymers and Nanoparticles on the Morphology of Self-Assembled Bulk Nanocomposites. Macromolecules 2007, 40, 8302–8310. [Google Scholar] [CrossRef]
- Tang, Q.Y.; Ma, Y.Q. Self-Assembly of Rod-Shaped Particles in Diblock-Copolymer Templates. J. Phys. Chem. B 2009, 113, 10117–10120. [Google Scholar] [CrossRef]
- Kim, S.; Yoo, M.; Kang, N.; Moon, B.; Kim, B.J.; Choi, S.H.; Kim, J.U.; Bang, J. Nanoporous Bicontinuous Structures via Addition of Thermally-Stable Amphiphilic Nanoparticles within Block Copolymer Templates. ACS Appl. Mater. Interfaces 2013, 5, 5659–5666. [Google Scholar] [CrossRef] [PubMed]
- Yao, L.; Lin, Y.; Watkins, J.J. Ultrahigh Loading of Nanoparticles into Ordered Block Copolymer Composites. Macromolecules 2014, 47, 1844–1849. [Google Scholar] [CrossRef]
- Halevi, A.; Halivni, S.; Oded, M.; Müller, A.H.E.; Banin, U.; Shenhar, R. Co-Assembly of A-B Diblock Copolymers with B′-type Nanoparticles in Thin Films: Effect of Copolymer Composition and Nanoparticle Shape. Macromolecules 2014, 47, 3022–3032. [Google Scholar] [CrossRef]
- Diaz, J.; Pinna, M.; Zvelindovsky, A.V.; Pagonabarraga, I. Phase Behavior of Block Copolymer Nanocomposite Systems. Adv. Theory Simul. 2018, 1, 1800066. [Google Scholar] [CrossRef]
- Singh, S.; Horechyy, A.; Yadav, S.; Formanek, P.; Hübner, R.; Srivastava, R.K.; Sapra, S.; Fery, A.; Nandan, B. Nanoparticle-Stabilized Perforated Lamellar Morphology in Block Copolymer/Quantum Dot Hybrids. Macromolecules 2021, 54, 1216–1223. [Google Scholar] [CrossRef]
- Bockstaller, M.R.; Lapetnikov, Y.; Margel, S.; Thomas, E.L. Size-Selective Organization of Enthalpic Compatibilized Nanocrystals in Ternary Block Copolymer/Particle Mixtures. J. Am. Chem. Soc. 2003, 125, 5276–5277. [Google Scholar] [CrossRef]
- Lo, C.T.; Chang, Y.C.; Wu, S.C.; Lee, C.L. Effect of particle size on the phase behavior of block copolymer/nanoparticle composites. Colloids Surf. A Physicochem. Eng. Asp. 2010, 368, 6–12. [Google Scholar] [CrossRef]
- Thompson, R.B. Predicting the Mesophases of Copolymer-Nanoparticle Composites. Science 2001, 292, 2469–2472. [Google Scholar] [CrossRef]
- Kim, J.U.; O’Shaughnessy, B. Nanoinclusions in Dry Polymer Brushes. Macromolecules 2006, 39, 413–425. [Google Scholar] [CrossRef]
- Krishnamoorti, R.; Vaia, R.A. Polymer nanocomposites. J. Polym. Sci. Part B Polym. Phys. 2007, 45, 3252–3256. [Google Scholar] [CrossRef]
- Schultz, A.J.; Hall, C.K.; Genzer, J. Computer Simulation of Block Copolymer/Nanoparticle Composites. Macromolecules 2005, 38, 3007–3016. [Google Scholar] [CrossRef]
- Detcheverry, F.A.; Kang, H.; Daoulas, K.C.; Müller, M.; Nealey, P.F.; de Pablo, J.J. Monte Carlo Simulations of a Coarse Grain Model for Block Copolymers and Nanocomposites. Macromolecules 2008, 41, 4989–5001. [Google Scholar] [CrossRef]
- Kang, H.; Detcheverry, F.A.; Mangham, A.N.; Stoykovich, M.P.; Daoulas, K.C.; Hamers, R.J.; Müller, M.; de Pablo, J.J.; Nealey, P.F. Hierarchical Assembly of Nanoparticle Superstructures from Block Copolymer-Nanoparticle Composites. Phys. Rev. Lett. 2008, 100, 148303. [Google Scholar] [CrossRef] [PubMed]
- Pryamitsyn, V.; Ganesan, V. Origins of Linear Viscoelastic Behavior of Polymer- Nanoparticle Composites. Macromolecules 2006, 39, 844–856. [Google Scholar] [CrossRef]
- Pryamitsyn, V.; Ganesan, V. Strong segregation theory of block copolymer- nanoparticle composites. Macromolecules 2006, 39, 8499–8510. [Google Scholar] [CrossRef]
- Thompson, R.B.; Ginzburg, V.V.; Matsen, M.W.; Balazs, A.C. Block Copolymer-Directed Assembly of Nanoparticles: Forming Mesoscopically Ordered Hybrid Materials. Macromolecules 2002, 35, 1060–1071. [Google Scholar] [CrossRef]
- Matsen, M.W.; Thompson, R.B. Particle Distributions in a Block Copolymer Nanocomposite. Macromolecules 2008, 41, 1853–1860. [Google Scholar] [CrossRef] [Green Version]
- Lee, J.Y.; Thompson, R.B.; Jasnow, D.; Balazs, A.C. Effect of Nanoscopic Particles on the Mesophase Structure of Diblock Copolymers. Macromolecules 2002, 35, 4855–4858. [Google Scholar] [CrossRef]
- Ohta, T.; Kawasaki, K. Equilibrium morphology of block copolymer melts. Macromolecules 1986, 19, 2621–2632. [Google Scholar] [CrossRef]
- Ohta, T.; Nozaki, H.; Doi, M. Computer simulations of domain growth under steady shear flow. J. Chem. Phys. 1990, 93, 2664–2675. [Google Scholar] [CrossRef]
- Leibler, L. Theory of Microphase Separation in Block Copolymers. Macromolecules 1980, 13, 1602–1617. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. I. Interfacial free energy. J. Chem. Phys. 1958, 28, 258–267. [Google Scholar] [CrossRef]
- Cahn, J.W. Free energy of a nonuniform system. II. Thermodynamic basis. J. Chem. Phys. 1959, 30, 1121–1124. [Google Scholar] [CrossRef]
- Cahn, J.W.; Hilliard, J.E. Free energy of a nonuniform system. III. Nucleation in a two-component incompressible fluid. J. Chem. Phys. 1959, 31, 688–699. [Google Scholar] [CrossRef]
- Cook, H.E. Brownian motion in spinodal decomposition. Acta Metall. 1970, 18, 297–306. [Google Scholar] [CrossRef]
- Bray, A.J. Theory of phase-ordering kinetics. Adv. Phys. 2002, 51, 481–587. [Google Scholar] [CrossRef] [Green Version]
- Sevink, G.J.A. Rigorous embedding of cell dynamics simulations in the Cahn-Hilliard-Cook framework: Imposing stability and isotropy. Phys. Rev. E 2015, 91, 053309. [Google Scholar] [CrossRef]
- Ren, S.R.; Hamley, I.W. Cell Dynamics Simulations of Microphase Separation in Block Copolymers. Macromolecules 2001, 34, 116–126. [Google Scholar] [CrossRef]
- Li, W.; Qiu, F.; Yang, Y.; Shi, A.C. Ordering dynamics of directed self-assembly of block copolymers in periodic two-dimensional fields. Macromolecules 2010, 43, 1644–1650. [Google Scholar] [CrossRef]
- Xie, N.; Li, W.; Qiu, F.; Shi, A.C. New strategy of nanolithography via controlled block copolymer self-assembly. Soft Matter 2013, 9, 536–542. [Google Scholar] [CrossRef]
- Hill, J.D.; Millett, P.C. Numerical simulations of directed self-assembly in diblock copolymer films using zone annealing and pattern templating. Sci. Rep. 2017, 7, 5250. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Xu, T.; Zvelindovsky, A.V.; Sevink, G.J.A.; Lyakhova, K.S.; Jinnai, H.; Russell, T.P. Electric Field Alignment of Asymmetric Diblock Copolymer Thin Films. Macromolecules 2005, 38, 10788–10798. [Google Scholar] [CrossRef]
- Pinna, M.; Zvelindovsky, A.V. Kinetic pathways of gyroid-to-cylinder transitions in diblock copolymers under external fields: Cell dynamics simulation. Soft Matter 2008, 4, 316–327. [Google Scholar] [CrossRef] [PubMed]
- Dessí, R.; Pinna, M.; Zvelindovsky, A.V. Cell Dynamics Simulations of Cylinder-Forming Diblock Copolymers in Thin Films on Topographical and Chemically Patterned Substrates. Macromolecules 2013, 46, 1923–1931. [Google Scholar] [CrossRef]
- Serral, M.; Pinna, M.; Zvelindovsky, A.V.; Avalos, J.B. Cell dynamics simulations of sphere-forming diblock copolymers in thin films on chemically patterned substrates. Macromolecules 2016, 49, 1079–1092. [Google Scholar] [CrossRef] [Green Version]
- Ginzburg, V.V.; Qiu, F.; Paniconi, M.; Peng, G.; Jasnow, D.; Balazs, A.C. Simulation of Hard Particles in a Phase-Separating Binary Mixture. Phys. Rev. Lett. 1999, 82, 4026–4029. [Google Scholar] [CrossRef] [Green Version]
- Ginzburg, V.V.; Gibbons, C.; Qiu, F.; Peng, G.; Balazs, A.C. Modeling the Dynamic Behavior of Diblock Copolymer/Particle Composites. Macromolecules 2000, 33, 6140–6147. [Google Scholar] [CrossRef]
- Ginzburg, V.V.; Peng, G.; Qiu, F.; Jasnow, D.; Balazs, A.C. Kinetic model of phase separation in binary mixtures with hard mobile impurities. Phys. Rev. E 1999, 60, 4352–4359. [Google Scholar] [CrossRef]
- Yan, L.T.; Schoberth, H.G.; Böker, A. Lamellar microstructure and dynamic behavior of diblock copolymer/nanoparticle composites under electric fields. Soft Matter 2010, 6, 5956–5964. [Google Scholar] [CrossRef]
- Yan, L.T.; Schoberth, H.G.; Böker, A. Large-Scale Oriented Assembly of Nanoparticles in Diblock Copolymer Templates under Electric Fields. Macromol. Chem. Phys. 2009, 210, 1003–1010. [Google Scholar] [CrossRef]
- Warren, P.B. Vapor-liquid coexistence in many-body dissipative particle dynamics. Phys. Rev. E 2003, 68, 066702. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Liu, D.; Zhong, C. Cooperative Self-Assembly of Nanoparticle Mixtures in Lamellar Diblock Copolymers: A Dissipative Particle Dynamics Study. Macromol. Rapid Commun. 2006, 27, 458–462. [Google Scholar] [CrossRef]
- Chen, H.; Ruckenstein, E. Structure and particle aggregation in block copolymer-binary nanoparticle composites. Polymer 2010, 51, 5869–5882. [Google Scholar] [CrossRef]
- Posocco, P.; Posel, Z.; Fermeglia, M.; Lísal, M.; Pricl, S. A molecular simulation approach to the prediction of the morphology of self-assembled nanoparticles in diblock copolymers. J. Mater. Chem. 2010, 20, 10511. [Google Scholar] [CrossRef]
- Maly, M.; Posocco, P.; Pricl, S.; Fermeglia, M. Self-Assembly of Nanoparticle Mixtures in Diblock Copolymers: Multiscale Molecular Modeling. Ind. Eng. Chem. Res. 2008, 47, 5023–5038. [Google Scholar] [CrossRef]
- Glotzer, S.C.; Solomon, M.J. Anisotropy of building blocks and their assembly into complex structures. Nat. Mater. 2007, 6, 557–562. [Google Scholar] [CrossRef]
- Damasceno, P.F.; Engel, M.; Glotzer, S.C. Predictive Self-Assembly of Polyhedra into Complex Structures. Science 2012, 337, 453–457. [Google Scholar] [CrossRef]
- Jiang, G.; Hore, M.J.A.; Gam, S.; Composto, R.J. Gold Nanorods Dispersed in Homopolymer Films: Optical Properties Controlled by Self-Assembly and Percolation of Nanorods. ACS Nano 2012, 6, 1578–1588. [Google Scholar] [CrossRef]
- Huynh, W.U.; Dittmer, J.J.; Alivisatos, A.P. Hybrid Nanorod-Polymer Solar Cells. Science 2002, 295, 2425–2427. [Google Scholar] [CrossRef] [Green Version]
- Murphy, C.J.; Orendorff, C.J. Alignment of Gold Nanorods in Polymer Composites and on Polymer Surfaces. Adv. Mater. 2005, 17, 2173–2177. [Google Scholar] [CrossRef]
- Gupta, S.; Zhang, Q.; Emrick, T.; Russell, T.P. “Self-corralling” nanorods under an applied electric field. Nano Lett. 2006, 6, 2066–2069. [Google Scholar] [CrossRef] [PubMed]
- Ryan, K.M.; Mastroianni, A.; Stancil, K.A.; Liu, H.; Alivisatos, A.P. Electric-Field-Assisted Assembly of Perpendicularly Oriented Nanorod Superlattices. Nano Lett. 2006, 6, 1479–1482. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Thorkelsson, K.; Mastroianni, A.J.; Ercius, P.; Xu, T. Direct Nanorod Assembly Using Block Copolymer-Based Supramolecules. Nano Lett. 2012, 12, 498–504. [Google Scholar] [CrossRef] [PubMed]
- Thorkelsson, K.; Bronstein, N.; Xu, T. Nanorod-Based Supramolecular Nanocomposites: Effects of Nanorod Length. Macromolecules 2016, 49, 6669–6677. [Google Scholar] [CrossRef]
- Deshmukh, R.D.; Liu, Y.; Composto, R.J. Two-Dimensional Confinement of Nanorods in Block Copolymer Domains. Nano Lett. 2007, 7, 3662–3668. [Google Scholar] [CrossRef] [PubMed]
- Tang, Z.; Zhang, Z.; Wang, Y.; Glotzer, S.C.; Kotov, N.A. Self-Assembly of CdTe Nanocrystals into Free-Floating Sheets. Science 2006, 314, 274–278. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lai, F.; Borca-Tasciuc, T.; Plawsky, J. Controlling directed self-assembly of gold nanorods in patterned PS-b-PMMA thin films. Nanotechnology 2015, 26, 055301. [Google Scholar] [CrossRef] [PubMed]
- Laicer, C.S.T.; Chastek, T.Q.; Lodge, T.P.; Taton, T.A. Gold Nanorods Seed Coaxial, Cylinder-Phase Domains from Block Copolymer Solutions. Macromolecules 2005, 38, 9749–9756. [Google Scholar] [CrossRef]
- Laicer, C.S.; Mrozek, R.A.; Taton, T.A. Domain nucleation dictates overall nanostructure in composites of block copolymers and model nanorods. Polymer 2007, 48, 1316–1328. [Google Scholar] [CrossRef]
- Ploshnik, E.; Salant, A.; Banin, U.; Shenhar, R. Co-assembly of block copolymers and nanorods in ultrathin films: Effects of copolymer size and nanorod filling fraction. Phys. Chem. Chem. Phys. 2010, 12, 11885. [Google Scholar] [CrossRef]
- Ploshnik, E.; Salant, A.; Banin, U.; Shenhar, R. Hierarchical Surface Patterns of Nanorods Obtained by Co-Assembly with Block Copolymers in Ultrathin Films. Adv. Mater. 2010, 22, 2774–2779. [Google Scholar] [CrossRef] [PubMed]
- Diaz, J.; Pinna, M.; Zvelindovsky, A.V.; Pagonabarraga, I.; Shenhar, R. Block Copolymer–Nanorod Co-assembly in Thin Films: Effects of Rod–Rod Interaction and Confinement. Macromolecules 2020, 53, 3234–3249. [Google Scholar] [CrossRef] [Green Version]
- Krook, N.M.; Ford, J.; Maréchal, M.; Rannou, P.; Meth, J.S.; Murray, C.B.; Composto, R.J. Alignment of Nanoplates in Lamellar Diblock Copolymer Domains and the Effect of Particle Volume Fraction on Phase Behavior. ACS Macro Lett. 2018, 7, 1400–1407. [Google Scholar] [CrossRef]
- He, L.; Zhang, L.; Chen, H.; Liang, H. The phase behaviors of cylindrical diblock copolymers and rigid nanorods’ mixtures. Polymer 2009, 50, 3403–3410. [Google Scholar] [CrossRef]
- He, L.; Zhang, L.; Xia, A.; Liang, H. Effect of nanorods on the mesophase structure of diblock copolymers. J. Chem. Phys. 2009, 130, 144907. [Google Scholar] [CrossRef] [PubMed]
- He, L.; Zhang, L.; Liang, H. Mono- or bidisperse nanorods mixtures in diblock copolymers. Polymer 2010, 51, 3303–3314. [Google Scholar] [CrossRef]
- Pan, Z.; He, L.; Zhang, L.; Liang, H. The dynamic behaviors of diblock copolymer/nanorod mixtures under equilibrium and nonequilibrium conditions. Polymer 2011, 52, 2711–2721. [Google Scholar] [CrossRef]
- Osipov, M.A.; Gorkunov, M.V. Spatial distribution and nematic ordering of anisotropic nanoparticles in lamellae and hexagonal phases of block copolymers. Eur. Phys. J. E 2016, 39, 126. [Google Scholar] [CrossRef]
- Osipov, M.A.; Gorkunov, M.V.; Kudryavtsev, Y.V. Induced orientational order of anisotropic nanoparticles in the lamellae phase of diblock copolymers. Mol. Cryst. Liq. Cryst. 2017, 647, 405–414. [Google Scholar] [CrossRef]
- Osipov, M.A.; Gorkunov, M.V.; Berezkin, A.V.; Kudryavtsev, Y.V. Phase behavior and orientational ordering in block copolymers doped with anisotropic nanoparticles. Phys. Rev. E 2018, 97, 042706. [Google Scholar] [CrossRef] [Green Version]
- Walther, A.; Müller, A.H. Janus particles. Soft Matter 2008, 4, 663–668. [Google Scholar] [CrossRef] [PubMed]
- Walther, A.; Matussek, K.; Müller, A.H.E. Engineering Nanostructured Polymer Blends with Controlled Nanoparticle Location using Janus Particles. ACS Nano 2008, 2, 1167–1178. [Google Scholar] [CrossRef] [PubMed]
- Pawar, A.B.; Kretzschmar, I. Fabrication, Assembly, and Application of Patchy Particles. Macromol. Rapid Commun. 2010, 31, 150–168. [Google Scholar] [CrossRef]
- Du, J.; O’Reilly, R.K. Anisotropic particles with patchy, multicompartment and Janus architectures: Preparation and application. Chem. Soc. Rev. 2011, 40, 2402–2416. [Google Scholar] [CrossRef]
- Walther, A.; Müller, A.H.E. Janus Particles: Synthesis, Self-Assembly, Physical Properties, and Applications. Chem. Rev. 2013, 113, 5194–5261. [Google Scholar] [CrossRef] [PubMed]
- Huang, Z.; Zhu, G.; Chen, P.; Hou, C.; Yan, L.T. Plastic Crystal-to-Crystal Transition of Janus Particles under Shear. Phys. Rev. Lett. 2019, 122, 198002. [Google Scholar] [CrossRef]
- Xu, K.; Guo, R.; Dong, B.; Yan, L.T. Directed self-assembly of Janus nanorods in binary polymer mixture: Towards precise control of nanorod orientation relative to interface. Soft Matter 2012, 8, 9581–9588. [Google Scholar] [CrossRef]
- Miller, W.L.; Cacciuto, A. Hierarchical self-assembly of asymmetric amphiphatic spherical colloidal particles. Phys. Rev. E 2009, 80, 021404. [Google Scholar] [CrossRef] [Green Version]
- Ren, B.; Kretzschmar, I. Viscosity-Dependent Janus Particle Chain Dynamics. Langmuir 2013, 29, 14779–14786. [Google Scholar] [CrossRef]
- Iwashita, Y.; Kimura, Y. Density dependence of orientational order in one-patch particles. Soft Matter 2017, 13, 4997–5007. [Google Scholar] [CrossRef]
- Beltran-Villegas, D.J.; Schultz, B.A.; Nguyen, N.H.; Glotzer, S.C.; Larson, R.G. Phase behavior of Janus colloids determined by sedimentation equilibrium. Soft Matter 2014, 10, 4593–4602. [Google Scholar] [CrossRef] [PubMed]
- DeLaCruz-Araujo, R.A.; Beltran-Villegas, D.J.; Larson, R.G.; Córdova-Figueroa, U.M. Shear-Induced Alignment of Janus Particle Lamellar Structures. Langmuir 2018, 34, 1051–1060. [Google Scholar] [CrossRef] [PubMed]
- Dong, B.; Huang, Z.; Chen, H.; Yan, L.T. Chain-Stiffness-Induced Entropy Effects Mediate Interfacial Assembly of Janus Nanoparticles in Block Copolymers: From Interfacial Nanostructures to Optical Responses. Macromolecules 2015, 48, 5385–5393. [Google Scholar] [CrossRef]
- Chen, P.; Yang, Y.; Dong, B.; Huang, Z.; Zhu, G.; Cao, Y.; Yan, L.T. Polymerization-Induced Interfacial Self-Assembly of Janus Nanoparticles in Block Copolymers: Reaction-Mediated Entropy Effects, Diffusion Dynamics, and Tailorable Micromechanical Behaviors. Macromolecules 2017, 50, 2078–2091. [Google Scholar] [CrossRef]
- Huang, M.; Li, Z.; Guo, H. The effect of Janus nanospheres on the phase separation of immiscible polymer blends via dissipative particle dynamics simulations. Soft Matter 2012, 8, 6834–6845. [Google Scholar] [CrossRef]
- Zhou, Y.; Huang, M.; Lu, T.; Guo, H. Nanorods with Different Surface Properties in Directing the Compatibilization Behavior and the Morphological Transition of Immiscible Polymer Blends in Both Shear and Shear-Free Conditions. Macromolecules 2018, 51, 3135–3148. [Google Scholar] [CrossRef]
- Zhou, C.; Luo, S.k.; Sun, Y.; Zhou, Y.; Qian, W. Dissipative particle dynamics studies on the interfacial tension of A/B homopolymer blends and the effect of Janus nanorods. J. Appl. Polym. Sci. 2016, 133, 44098. [Google Scholar] [CrossRef]
- Yang, Q.; Loos, K. Design and Fabrication of Janus Nanoparticles for Interfacial Distribution in Block Copolymers. Macromol. Chem. Phys. 2017, 218, 1600451. [Google Scholar] [CrossRef]
- Yang, Q.; Loos, K. Janus nanoparticles inside polymeric materials: Interfacial arrangement toward functional hybrid materials. Polym. Chem. 2017, 8, 641–654. [Google Scholar] [CrossRef] [Green Version]
- Pinna, M.; Pagonabarraga, I.; Zvelindovsky, A.V. Modeling of Block Copolymer/Colloid Hybrid Composite Materials: Modeling of Block Copolymer/Colloid Hybrid Composite Materials. Macromol. Theory Simul. 2011, 20, 769–779. [Google Scholar] [CrossRef]
- Diaz, J.; Pinna, M.; Zvelindovsky, A.V.; Asta, A.; Pagonabarraga, I. Cell Dynamic Simulations of Diblock Copolymer/Colloid Systems. Macromol. Theory Simul. 2017, 26, 1600050. [Google Scholar] [CrossRef] [Green Version]
- Ball, R.C.; Essery, R.L.H. Spinodal decomposition and pattern formation near surfaces. J. Phys. Condens. Matter 1990, 2, 10303–10320. [Google Scholar] [CrossRef]
- Hamley, I.W. Cell dynamics simulations of block copolymers. Macromol. Theory Simul. 2000, 9, 363–380. [Google Scholar] [CrossRef]
- Ren, S.R.; Hamley, I.W.; Sevink, G.J.A.; Zvelindovsky, A.V.; Fraaije, J.G.E.M. Mesoscopic Simulations of Lamellar Orientation in Block Copolymers. Macromol. Theory Simul. 2002, 11, 123–127. [Google Scholar] [CrossRef]
- Sevink, G.J.A.; Pinna, M.; Langner, K.M.; Zvelindovsky, A.V. Selective disordering of lamella-forming diblock copolymers under an electric field. Soft Matter 2011, 7, 5161. [Google Scholar] [CrossRef]
- Pinna, M.; Schreier, L.; Zvelindovsky, A.V. Mechanisms of electric-field-induced alignment of block copolymer lamellae. Soft Matter 2009, 5, 970. [Google Scholar] [CrossRef] [Green Version]
- Oono, Y.; Puri, S. Computationally efficient modeling of ordering of quenched phases. Phys. Rev. Lett. 1987, 58, 836–839. [Google Scholar] [CrossRef]
- Puri, S.; Oono, Y. Study of phase-separation dynamics by use of cell dynamical systems. II. Two-dimensional demonstrations. Phys. Rev. A 1988, 38, 1542–1565. [Google Scholar] [CrossRef]
- Bahiana, M.; Oono, Y. Cell dynamical system approach to block copolymers. Phys. Rev. A 1990, 41, 6763–6771. [Google Scholar] [CrossRef]
- Oono, Y.; Puri, S. Study of phase-separation dynamics by use of cell dynamical systems. I. Modeling. Phys. Rev. A 1988, 38, 434–453. [Google Scholar] [CrossRef]
- Pinna, M.; Zvelindovsky, A.V. Large scale simulation of block copolymers with cell dynamics. Eur. Phys. J. B 2012, 85, 210. [Google Scholar] [CrossRef]
- Tanaka, H.; Araki, T. Simulation method of colloidal suspensions with hydrodynamic interactions: Fluid particle dynamics. Phys. Rev. Lett. 2000, 85, 1338. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Pinna, M.; Guo, X.; Zvelindovsky, A.V. Block copolymer nanoshells. Polymer 2008, 49, 2797–2800. [Google Scholar] [CrossRef]
- Pinna, M.; Hiltl, S.; Guo, X.; Böker, A.; Zvelindovsky, A.V. Block Copolymer Nanocontainers. ACS Nano 2010, 4, 2845–2855. [Google Scholar] [CrossRef]
- Donev, A.; Burton, J.; Stillinger, F.H.; Torquato, S. Tetratic order in the phase behavior of a hard-rectangle system. Phys. Rev. B 2006, 73, 054109. [Google Scholar] [CrossRef] [Green Version]
- Han, Y.; Alsayed, A.M.; Nobili, M.; Zhang, J.; Lubensky, T.C.; Yodh, A.G. Brownian Motion of an Ellipsoid. Science 2006, 314, 626–630. [Google Scholar] [CrossRef] [Green Version]
- Diaz, J.; Pinna, M.; Zvelindovsky, A.V.; Pagonabarraga, I. Nonspherical Nanoparticles in Block Copolymer Composites: Nanosquares, Nanorods, and Diamonds. Macromolecules 2019, 52, 8285–8294. [Google Scholar] [CrossRef] [Green Version]
- Peng, G.; Qiu, F.; Ginzburg, V.V.; Jasnow, D.; Balazs, A.C. Forming Supramolecular Networks from Nanoscale Rods in Binary, Phase-Separating Mixtures. Science 2000, 288, 1802–1804. [Google Scholar] [CrossRef]
- Krekhov, A.; Weith, V.; Zimmermann, W. Periodic structures in binary mixtures enforced by Janus particles. Phys. Rev. E 2013, 88, 040302. [Google Scholar] [CrossRef] [Green Version]
- Guo, Y.Q.; Pan, J.X.; Sun, M.N.; Zhang, J.J. Phase transition of a symmetric diblock copolymer induced by nanorods with different surface chemistry. J. Chem. Phys. 2017, 146, 024902. [Google Scholar] [CrossRef]
- Guo, Y.Q. Phase transition of asymmetric diblock copolymer induced by nanorods of different properties. Chin. Phys. B 2021, 30, 048301. [Google Scholar] [CrossRef]
- Gay, J.G.; Berne, B.J. Modification of the overlap potential to mimic a linear site-site potential. J. Chem. Phys. 1981, 74, 3316–3319. [Google Scholar] [CrossRef]
- Berne, B.J.; Pechukas, P. Gaussian Model Potentials for Molecular Interactions. J. Chem. Phys. 1972, 56, 4213–4216. [Google Scholar] [CrossRef]
- De Miguel, E.; Rull, L.F.; Chalam, M.K.; Gubbins, K.E. Liquid crystal phase diagram of the Gay-Berne fluid. Mol. Phys. 1991, 74, 405–424. [Google Scholar] [CrossRef]
- Berardi, R.; Emerson, A.P.J.; Zannoni, C. Monte Carlo investigations of a Gay—Berne liquid crystal. J. Chem. Soc. Faraday Trans. 1993, 89, 4069–4078. [Google Scholar] [CrossRef]
- Gottschalk, S.; Lin, M.C.; Manocha, D. OBBTree: A Hierarchical Structure for Rapid Interference Detection. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, SIGGRAPH ’96, Virtual Event, 9–13 August 2021; ACM: New York, NY, USA, 1996; pp. 171–180. [Google Scholar] [CrossRef]
- Diaz, J.; Pinna, M.; Zvelindovsky, A.V.; Pagonabarraga, I. Nematic Ordering of Anisotropic Nanoparticles in Block Copolymers. Adv. Theory Simul. 2022, 5, 2100433. [Google Scholar] [CrossRef]
- Diaz, J.; Pinna, M.; Zvelindovsky, A.; Pagonabarraga, I. Co-assembly of Janus nanoparticles in block copolymer systems. Soft Matter 2019, 15, 6400–6410. [Google Scholar] [CrossRef]
- Guo, X.; Pinna, M.; Zvelindovsky, A.V. Parallel Algorithm for Cell Dynamics Simulation of Block Copolymers. Macromol. Theory Simul. 2007, 16, 779–784. [Google Scholar] [CrossRef]
- Fanfarillo, A.; Burnus, T.; Cardellini, V.; Filippone, S.; Nagle, D.; Rouson, D. OpenCoarrays: Open-source transport layers supporting coarray Fortran compilers. In Proceedings of the 8th International Conference on Partitioned Global Address Space Programming Models, Eugene, OR, USA, 6–10 October 2014; pp. 1–11. [Google Scholar]
- Fanfarillo, A.; Garain, S.K.; Balsara, D.; Nagle, D. Resilient computational applications using Coarray Fortran. Parallel Comput. 2019, 81, 58–67. [Google Scholar] [CrossRef]
- Diaz, J.; Pinna, M.; Zvelindovsky, A.V.; Pagonabarraga, I. Parallel Hybrid Simulations of Block Copolymer Nanocomposites using Coarray Fortran. Macromol. Theory Simul. 2021, 30, 2100007. [Google Scholar] [CrossRef]
- Seaton, M.A.; Anderson, R.L.; Metz, S.; Smith, W. DL_MESO: Highly scalable mesoscale simulations. Mol. Simul. 2013, 39, 796–821. [Google Scholar] [CrossRef]
- Matsen, M.W. Phase Behavior of Block Copolymer/Homopolymer Blends. Macromolecules 1995, 28, 5765–5773. [Google Scholar] [CrossRef]
- Janert, P.K.; Schick, M. Phase Behavior of Binary Homopolymer/Diblock Blends: Temperature and Chain Length Dependence. Macromolecules 1998, 31, 1109–1113. [Google Scholar] [CrossRef]
- Kim, J.U.; O’Shaughnessy, B. Morphology Selection of Nanoparticle Dispersions by Polymer Media. Phys. Rev. Lett. 2002, 89, 238301. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kim, B.J.; Fredrickson, G.H.; Bang, J.; Hawker, C.J.; Kramer, E.J. Tailoring Core- Shell Polymer-Coated Nanoparticles as Block Copolymer Surfactants. Macromolecules 2009, 42, 6193–6201. [Google Scholar] [CrossRef]
- Xu, M.; Ku, K.H.; Lee, Y.J.; Shin, J.J.; Kim, E.J.; Jang, S.G.; Yun, H.; Kim, B.J. Entropy-Driven Assembly of Nanoparticles within Emulsion-Evaporative Block Copolymer Particles: Crusted, Seeded, and Alternate-Layered Onions. Chem. Mater. 2020, 32, 7036–7043. [Google Scholar] [CrossRef]
- Diaz, J.; Pinna, M.; Zvelindovsky, A.V.; Pagonabarraga, I. Large scale three dimensional simulations of hybrid block copolymer/nanoparticle systems. Soft Matter 2019, 15, 9325–9335. [Google Scholar] [CrossRef] [Green Version]
- Ohta, T.; Ito, A. Dynamics of phase separation in copolymer-homopolymer mixtures. Phys. Rev. E 1995, 52, 5250–5260. [Google Scholar] [CrossRef]
- Avalos, E.; Teramoto, T.; Komiyama, H.; Yabu, H.; Nishiura, Y. Transformation of block copolymer nanoparticles from ellipsoids with striped lamellae into onionlike spheres and dynamical control via coupled Cahn–Hilliard equations. ACS Omega 2018, 3, 1304–1314. [Google Scholar] [CrossRef]
- Thorkelsson, K.; Nelson, J.H.; Alivisatos, A.P.; Xu, T. End-to-End Alignment of Nanorods in Thin Films. Nano Lett. 2013, 13, 4908–4913. [Google Scholar] [CrossRef] [Green Version]
- Całus, S.; Rau, D.; Huber, P.; Kityk, A.V. Influence of nanoconfinement on the nematic behavior of liquid crystals. Phys. Rev. E 2012, 86, 021701. [Google Scholar] [CrossRef] [Green Version]
- Diaz, J.; Pinna, M.; Zvelindovsky, A.V.; Pagonabarraga, I. Nanoparticle anisotropy induces sphere-to-cylinder phase transition in block copolymer melts. Soft Matter 2022. [Google Scholar] [CrossRef]
- Gorkunov, M.V.; Osipov, M.A. Mean-field theory of a nematic liquid crystal doped with anisotropic nanoparticles. Soft Matter 2011, 7, 4348–4356. [Google Scholar] [CrossRef]
- Burgos-Mármol, J.J.; Patti, A. Molecular Dynamics of Janus Nanodimers Dispersed in Lamellar Phases of a Block Copolymer. Polymers 2021, 13, 1524. [Google Scholar] [CrossRef] [PubMed]
- Rasin, B.; Lindsay, B.J.; Ye, X.; Meth, J.S.; Murray, C.B.; Riggleman, R.A.; Composto, R.J. Nanorod position and orientation in vertical cylinder block copolymer films. Soft Matter 2020, 16, 3005–3014. [Google Scholar] [CrossRef] [PubMed]
- Lu, F.; Yager, K.G.; Zhang, Y.; Xin, H.; Gang, O. Superlattices assembled through shape-induced directional binding. Nat. Commun. 2015, 6, 6912. [Google Scholar] [CrossRef] [Green Version]





















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Diaz, J.; Pinna, M.; Zvelindovsky, A.V.; Pagonabarraga, I. Hybrid Time-Dependent Ginzburg–Landau Simulations of Block Copolymer Nanocomposites: Nanoparticle Anisotropy. Polymers 2022, 14, 1910. https://doi.org/10.3390/polym14091910
Diaz J, Pinna M, Zvelindovsky AV, Pagonabarraga I. Hybrid Time-Dependent Ginzburg–Landau Simulations of Block Copolymer Nanocomposites: Nanoparticle Anisotropy. Polymers. 2022; 14(9):1910. https://doi.org/10.3390/polym14091910
Chicago/Turabian StyleDiaz, Javier, Marco Pinna, Andrei V. Zvelindovsky, and Ignacio Pagonabarraga. 2022. "Hybrid Time-Dependent Ginzburg–Landau Simulations of Block Copolymer Nanocomposites: Nanoparticle Anisotropy" Polymers 14, no. 9: 1910. https://doi.org/10.3390/polym14091910
APA StyleDiaz, J., Pinna, M., Zvelindovsky, A. V., & Pagonabarraga, I. (2022). Hybrid Time-Dependent Ginzburg–Landau Simulations of Block Copolymer Nanocomposites: Nanoparticle Anisotropy. Polymers, 14(9), 1910. https://doi.org/10.3390/polym14091910