1. Introduction
The paper focuses on cyclic experiments of polymer composites with textile reinforcements (called as cords), which are used for automobile transport in the interior and especially in tire manufacturing. The authors have been devoted to tire casings and tires for a long time. Therefore, tire casing materials are used for this research. Tires are one point of contact between the vehicle and the road surface [
1], ensuring the transmission of forces and moments [
2] and also contributing to the suspension of the vehicle. The tire consists of a tire casing and a rim. An automobile radial tire casing with classical construction [
3] consists of rubber with textile and steel cords [
4] in a tire crown and carcass,
Figure 1. The construction parts applied to the radial tire casings of the passenger car are a steel cord belt, a textile carcass, and a textile overlap belt [
5,
6]. These construction parts are themselves composites, consisting of one or several plies. The description of the tire casing with details of the microstructures of the reinforcing ply is given in the publication [
6]. Information about the cord materials used and the number of plies in the sidewall and under the tread of the tire casing can be found on the tire sidewall. There is one polyester layer in the sidewall of a passenger car tire and four construction layers in the crown of the tire casing, namely [
6]: one polyester layer, two steel layers, and one polyamide layer. The different materials applied for the textile reinforcements in the textile carcass and a textile overlap belt are listed in
Table 1 and are also determined by the purpose of the shell, e.g., for sports purposes, aramid as a cord material is preferable.
For the overlap belt, polyamide PA66 140 × 1 × 2 is used as a typical construction of textile reinforcement [
6]. The density of the textile ply is the number of ends per one meter of width. Density is referred to as EPM. The typical density value is in the range of 1000 m
−1 to 1200 m
−1. As a sample, the EPM of the textile overlap belt of the Dunlop 215/40 R17 87V Extra load SS SPORT MAXX tire casing is approximately 1400 m
−1. The diameter of the cords is 0.44 mm, and the thickness of the overlap belt is 1.1 mm. The main geometric parameters of the construction parts of Dunlop 215/40 R17 tire casings as diameters of cords are shown in
Table 2. The parameters of the reinforcements of the Continental 245/40 R18 97Y Extra load ContiSportContact 3 tire casing are in
Table 3; the parameters are different. The textile carcass data in
Table 2 and
Table 3 are important for the preparation of one-layer composite specimens.
Statical tensile tests of composite specimens are important for obtaining knowledge about stiffness characteristics and material parameters. Cyclic loading tests of composite parts of tire casings and textile cords are requested for the verification analysis between experiments and computational simulation of tires and as input data (about cords) to simulations under dynamic loading. Tests of specific polymer composites with an elastomer matrix are not standardized. The paper [
7] describes the geometric parameters of single-layer tire casing specimens with different cord-angles (0°, 25°, 45°, 60°, and 90°) for uniaxial tensile tests. Some standards describe the test procedure and testing conditions, the shape, and the geometric parameters of the test specimens for static tensile tests of composites [
8,
9]. The ASTM D-3039-76 standard [
10] describes the width of fiber-resin composite test specimens in the form of strips 25 mm wide and 2–4 mm thick with a working length of 150 mm. Therefore, for cyclic loading tests, the shape of specimens of a single layer with textile cords and elastomer must be designed. For textile materials and fibers, the DIN 53835-13 standard [
11] defines conditions for cycle loading for the first five cycles. This standard can be used for PA66 cords. Next, it is possible to rely on knowledge of the literature focused on the specific loading of polymers, e.g., [
12].
The aim of the authors’ research is to propose experimental methods for composites and textile cords that simulate the real cycle states of operational loading during tire running. The cyclic loading tests of composites are requested for verification analyses between tests and the computational simulation of tires too. On the basis of the literature search, it can be concluded that there is no similar publicly available publication that deals with the design of methods for low-cycle loading of polymer composites and tire cords with the aim of mathematical interpretation of the results and the application of a video-extensometer.
3. Results and Discussion
3.1. Cyclic Tests of Composites
The dependences of true stress on strain on the video-extensometer (and for comparison, true stress on strain between jaws) are in
Figure 4, and for fifth cycles, they are in
Figure 5, which are result dependences for practical use. These dependencies (
Figure 5) can be used as input material data, which describes a textile cap ply for computational simulation of a textile carcass of a sports bike tire with PA66, where it was necessary to solve the material parameters for the simulation of dynamic loading conditions. True stress is defined as the stress obtained by the ratio of the current tensile force to the current cross section of the test specimen obtained based on the change in width measured by the video-extensometer.
The true stress values for the maximum strain of the fifth cycle of the loops are in
Table 5. Based on the results (
Figure 6), there is a relationship between stress and the number of cycle loops as shown by the second-degree polynomial curve with an R-squared of 1:
where
NoL—number of cycle loop.
The relationship can be used to predict the true stress for the next cycle loop under the same testing conditions. For example, if it is necessary to know the stress value for the end of the fifth cycle for the sixth loop of the composite for computational modeling, then the stress value could be 6.8 MPa according to the relationship (1).
Furthermore, it was also necessary to verify the scientific hypothesis and determine whether it is already possible to consider the fourth cycle as stable. The fourth cycle can be considered a stable cycle if the percentage change in the maximum true stress between the fourth and fifth cycles is less than 2%. The percentage changes of maximum true stress between the second and third cycles, between the third and fourth cycles, and between the fourth and fifth cycles are in
Table 6.
Based on the results, the fourth cycle can be considered a stable cycle because the percentage change in the maximum true stress between the fourth and fifth cycles is 1.6%.
3.2. Cyclic Tests of Textile Cords—Relaxation Stress and Creep
The evaluation will be in terms of the dependence of the force on the strain between the jaws. For textile materials, stress in MPa is not considered, but in e.g., cN·tex
−1. Therefore, knowledge of force is important from cycle loading tests.
Figure 7 shows the dependence on the test without relaxation and the use of the video-extensometer. The method with 15% (preload 2.35 N and 10 mm·min
−1, the specimen with an initial length of 250 mm between jaws, loading to 15% strain, unloading to 5 N) was used with a loading speed 250 mm·min
−1. The force is 44.22 N at a strain of 14.94% for the fifth cycle.
Figure 8 shows the results of tests with the same conditions, only with relaxation, stress, and creep for 120 s. The right curve with creep is shifted on the
x-axis by 4% to the right for better comparison. Relaxation stress (specimen No. 1): force change after a time of 120 s is 3.89 N (force after the fifth cycle is 41.21 N, force after relaxation time is 37.32 N). It changes about 9.4% of force after the fifth cycle. Creep (specimen No. 2): strain change after a time of 120 s is 0.69% (strain after the fifth cycle is 14.9%, strain after relaxation time is 15.59%). It is a change of about 4.6% of strain after the fifth cycle 14.9%.
Force values after individual cycles are in
Table 7.
Figure 9 is a relationship between force (for the second to the fifth cycles) and number of cycles as a linear dependence with R-squared of 0.994:
where
NoC—number of cycle loop,
F1st—force of the 1st cycle.
Furthermore, the method with 20% strain was changed to compare the results with the method with 15%. A comparison of the dependences between force and strain between jaws is shown in
Figure 10. The method is with creep. Force values after individual cycles are in
Table 8.
After the fifth cycle: 56.79 N (19.96%) and 43.79 N (14.9%). After a force hold for 120 s: the strain is changed to 20.73% and 15.59%, and the force is 57.16 N for the strain of 20.73%. The strain changes are 0.77% (method with 20%) and 0.69% (method with 15%).
Based on the results, there is a relationship between force and number of cycles:
Thus, the number 0.51 in the formula for the 20% method is different from that for 15% (the value in the formula was 0.38). Here, it is interesting that if for the 15% method 15 is divided by the coefficient 0.38 = the result is 39.47. A similar result is obtained for the 20% method, i.e., 20% divided by 0.51 = the result is 39.22. So, based on this, it can be deduced that if the experiment was carried out for another method, e.g., 25% method, then the formula would be the same, only the coefficient of the NoC multiplier would be approx. 0.63 (it is 25/39.47).
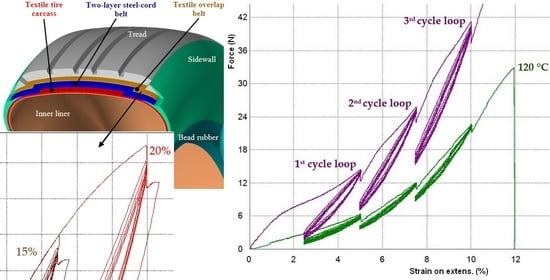
3.3. Cyclic Tests of Textile Cords—Temperature Influences
The test results as force-strain on video-extensometer dependences by method with three cycle loops for two temperatures (the temperature chamber was used) are in
Figure 11. The relaxation time was in each cycle loop. The dependencies can be used as input material data for textile cords in the computational simulations of tire casings using a custom material model definition. Software tools used for computational simulation will typically allow for the definition of custom material models.
The force values after relaxation time for each cycle loop are in
Table 9. The transformation of force values to stress values is given in
Table 9. The fineness (linear density) of the textile-conditioned cord is 944 dtex; therefore, stress can be obtained as force divided fitness. The unit of stress is deliberately adjusted so that the calculated stress values are in the range from 0 to 100 for better comparison of the values with each other. Therefore, the stress for textile materials is given in multiples of the force unit, e.g., in cN (100 cN is 1 N), divided by fineness, e.g., in tex instead of dtext (10 tex is 1 dtex). In our case, we chose the unit of stress as cN·tex
−1.
The force-time dependences are shown in
Figure 12. Tenacities (the tensile stress expressed as force per unit fineness) for nine specimens are 75.99 ± 1.84 cN·tex
−1 for a temperature of 20 °C and 37.22 ± 2.85 cN·tex
−1 for a temperature of 120 °C, and the ductility (strains at break) are 17.79 ± 0.5% for a temperature of 20 °C and 12.11 ± 0.52% for a temperature of 120 °C. The values for a temperature of 20 °C are different from cord producer values [
10], but they are closer to the data from the patent [
20], which deals with the cord construction PA66 470 × 2 (it means fineness is 940 dtex). The tenacity for a temperature of 20 °C reported in literature [
13] is 86.2 cN·tex
−1, and the ductility (referred to in this literature as elongation at break) is 18.6%. The difference in measured tenacity from the manufacturer’s published [
13] is 11.8%, and the difference in ductility is 4.4%. Based on patent [
20], tenacity obtained from a breaking force of 73 N is 77.66 cN·tex
−1, and ductility is 18%.
4. Conclusions
New methods are presented as possible test references for studying composites and textile cords. On the basis of the results, the fourth cycle in every cycle loop can be considered a stable cycle for polymer composites with PA66 cords because the change in the maximum true stress between the fourth and fifth cycles is 1.6%. The method for textile cords considers stress relaxation.
A simple and fast relationship is found that describes the value of the force at each end of the cycles for a textile cord. It can be used to predict forces for specific strains and can be used for practical use. These preliminary results point to the possibility of further research into textile material properties. The results of the polymer composite and textile cord tests provide a better understanding of the mechanical properties under cyclic loading.
The paper evaluated the effect of temperatures on the material properties of textile cord and the relaxation effect, which is important for the assessment of practical applications. Knowledge of this effect is important to assess the change in material parameters that occurs during the vulcanization process of tire casings.
The obtained equations can be used to determine input data for computational simulation. It would be appropriate for further research to apply a video-extensometer for online monitoring and recording of deformations on the surfaces of test specimens during cyclic loading tests. For composite specimens, the authors recommend also performing biaxial cyclic load tests that would be even closer to real load conditions.