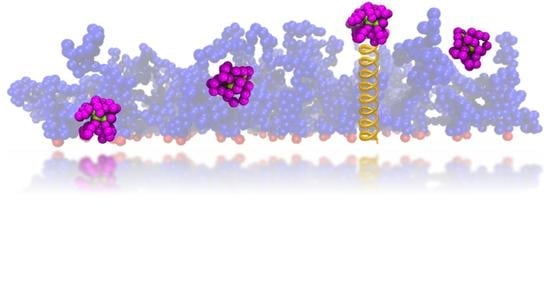
Globular Proteins and Where to Find Them within a Polymer Brush—A Case Study
Abstract
:1. Introduction
2. Model and Methods
2.1. Coarse-Grained Model and Simulation Setup
2.1.1. Brush Setup
2.1.2. Protein Setup
2.1.3. Coating Setup with Backbone Attractive Beads
2.1.4. Coating Setup with Terminal Attractive Beads
2.1.5. Coating Setup with Ligands
3. Results and Discussion
3.1. Rate and Percentage of Protein Adsorption
3.1.1. Effect of the Grafting Density
3.1.2. Effect of the Hydrophobicity Ratio
3.1.3. Effect of the Position of Attractive A-Beads at the Backbone
3.1.4. Effect of the Presence of Terminal Attractive A-Beads
3.1.5. Effect of the Presence of the Ligands and Their Surface Density
3.2. Protein Density Profiles
3.2.1. Effect of the Grafting Densities
3.2.2. Effect of the Hydrophobicity Ratio
3.2.3. Effect of the Position of the Attractive A-Beads at the Backbone
3.2.4. Effect of the Presence of Terminal Attractive A-Beads
3.2.5. Effect of the Presence of the Ligands and Their Surface Density
3.3. Shape of the Proteins
3.4. Potential of Mean Force (PMF)
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Supplementary Data for the Effect of A-Bead Position at the Backbone


Appendix B. Mobile versus Immobile A-Beads

Appendix C. Hydrophobic versus Hydrophilic A-Beads


References
- Hsieh, S.R.; Reddy, P.M.; Chang, C.J.; Kumar, A.; Wu, W.C.; Lin, H.Y. Exploring the Behavior of Bovine Serum Albumin in Response to Changes in the Chemical Composition of Responsive Polymers: Experimental and Simulation Studies. Polymers 2016, 8, 238. [Google Scholar] [CrossRef] [PubMed]
- Gago, D.; Corvo, M.C.; Chagas, R.; Ferreira, F.M.; Coelhoso, I. Protein adsorption performance of a novel functionalized cellulose-based polymer. Polymers 2022, 14, 5122. [Google Scholar] [CrossRef] [PubMed]
- Solveyra, E.G.; Thompson, D.H.; Szleifer, I. Proteins adsorbing onto surface-modified nanoparticles: Effect of surface curvature, pH, and the interplay of pPolymers and proteins acid-base equilibrium. Polymers 2022, 14, 739. [Google Scholar] [CrossRef] [PubMed]
- March, D.; Bianco, V.; Franzese, G. Protein unfolding and aggregation near a hydrophobic interface. Polymers 2021, 13, 156. [Google Scholar] [CrossRef] [PubMed]
- Szleifer, I.; Carignano, M.A. Tethered polymer layers: Phase transitions and reduction of protein adsorption. Macromol. Rapid Commun. 2000, 21, 423–448. [Google Scholar] [CrossRef]
- Levinthal, C. Are there pathways for protein folding? J. Chem. Phys. 1968, 65, 44–45. [Google Scholar] [CrossRef]
- Levinthal, C. How to fold graciously. In Mossbauer Spectroscopy in Biological Systems, Proceedings of the Meeting held at Allerton House, Monticello, IL, USA, 17–18 March 1969; University of Illinois Press: Urbana, IL, USA, 1969; pp. 22–24. [Google Scholar]
- Banerjee, J.; Radvar, E.; Azevedo, H.S. 10—Self-assembling peptides and their application in tissue engineering and regenerative medicine. In Peptides and Proteins as Biomaterials for Tissue Regeneration and Repair; Woodhead Publishing: Sawston, UK, 2018; pp. 245–281. [Google Scholar]
- Skipper, L. Proteins | Overview. In Encyclopedia of Analytical Science, 2nd ed.; Worsfold, P., Townshend, A., Poole, C., Eds.; Elsevier: Amsterdam, The Netherlands, 2005; pp. 344–352. [Google Scholar]
- Sun, P.D.; Foster, C.E.; Boyington, J.C. Overview of protein structural and functional folds. Curr. Protoc. Protein Sci. 2004, 35, 17.1.1–17.1.189. [Google Scholar] [CrossRef]
- Shen, C.H. (Ed.) Gene Expression: Translation of the Genetic Code. In Diagnostic Molecular Biology; Academic Press: Cambridge, MA, USA, 2019; Chapter 4; pp. 87–116. [Google Scholar]
- Wills, E.D. (Ed.) Muscle. In Biochemical Basis of Medicine; Butterworth-Heinemann: Oxford, UK, 1985; Chapter 31; pp. 382–394. [Google Scholar]
- Blossom, S.J. Autoimmune disease and epigenetics. In Medical Epigenetics, 2nd ed.; Tollefsbol, T.O., Ed.; Translational Epigenetics; Academic Press: Cambridge, MA, USA, 2021; Chapter 9; Volume 29, pp. 171–183. [Google Scholar]
- Paul, F.; Wehmeyer, C.; Abualrous, E.T.; Wu, H.; Crabtree, M.; Schöneberg, J.; Clarke, J.; Freund, C.; Weikl, T.R.; Noé, F. Protein-peptide association kinetics beyond the seconds timescale from atomistic simulations. Nat. Commun. 2017, 8, 1095. [Google Scholar] [CrossRef]
- Best, R.B.; Hummer, G.; Eaton, W. Native contacts determine protein folding mechanisms in atomistic simulations. Proc. Natl. Acad. Sci. USA 2013, 110, 17874–17879. [Google Scholar] [CrossRef]
- Best, R. Atomistic molecular simulations of protein folding. Curr. Opin. Struct. Biol. 2012, 22, 52–61. [Google Scholar] [CrossRef]
- Shaw, D.E.; Maragakis, P.; Lindorff-Larsen, K.; Piana, S.; Dror, R.O.; Eastwood, M.P.; Bank, J.; Jumper, J.; Salmon, J.; Shan, Y.; et al. Atomic-Level Characterization of the Structural Dynamics of Proteins. Science 2010, 330, 341–346. [Google Scholar] [CrossRef] [PubMed]
- Lindorff-Larsen, K.; Piana, S.; Dror, R.; Shaw, D. How fast-folding proteins fold. Science 2011, 334, 517–520. [Google Scholar] [CrossRef] [PubMed]
- García, A.; Onuchic, J. Folding a protein in a computer: An atomic description of the folding/unfolding of protein A. Proc. Natl. Acad. Sci. USA 2003, 100, 13898–13903. [Google Scholar] [CrossRef] [PubMed]
- Best, R.B.; Mittal, J. Microscopic events in β-hairpin folding from alternative unfolded ensembles. Proc. Natl. Acad. Sci. USA 2011, 108, 11087–11092. [Google Scholar] [CrossRef]
- Pande, V.S.; Baker, I.; Chapman, J.; Elmer, S.P.; Khaliq, S.; Larson, S.M.; Rhee, Y.M.; Shirts, M.R.; Snow, C.D.; Sorin, E.J.; et al. Atomistic protein folding simulations on the submillisecond time scale using worldwide distributed computing. Biopolymers 2003, 68, 91–109. [Google Scholar] [CrossRef]
- Elcock, A.H. Atomic-level observation of macromolecular crowding effects: Escape of a protein from the GroEL cage. Proc. Natl. Acad. Sci. USA 2003, 100, 2340–2344. [Google Scholar] [CrossRef]
- Ravichandran, S.; Madura, J.D.; Talbot, J. A Brownian dynamics study of the initial stages of hen egg-white lysozyme adsorption at a solid interface. J. Phys. Chem. B 2001, 105, 3610–3613. [Google Scholar] [CrossRef]
- Raffaini, G.; Ganazzoli, F. Molecular dynamics simulation of the adsorption of a fibronectin module on a graphite surface. Langmuir 2004, 20, 3371–3378. [Google Scholar] [CrossRef]
- Boughton, A.P.; Andricioaei, I.; Chen, Z. Surface orientation of magainin 2: Molecular dynamics simulation and sum frequency generation vibrational spectroscopic studies. Langmuir 2010, 26, 16031–16036. [Google Scholar] [CrossRef]
- Chu, J.W.; Voth, G.A. Coarse-Grained Modeling of the Actin Filament Derived from Atomistic-Scale Simulations. Biophys. J. 2006, 90, 1572–1582. [Google Scholar] [CrossRef]
- Levitt, M. A simplified representation of protein conformations for rapid simulation of protein folding. J. Mol. Biol. 1976, 104, 59–107. [Google Scholar] [CrossRef] [PubMed]
- Levitt, M.; Warshel, A. Computer simulation of protein folding. Nature 1975, 253, 694–698. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, S.; Scheraga, H. Medium- and Long-Range Interaction Parameters between Amino Acids for Predicting Three-Dimensional Structures of Proteins. Macromolecules 1976, 9, 945–950. [Google Scholar] [CrossRef] [PubMed]
- Miyazawa, S.; Jernigan, R.L. Estimation of effective interresidue contact energies from protein crystal structures: Quasi-chemical approximation. Macromolecules 1985, 18, 534–552. [Google Scholar] [CrossRef]
- Buchete, N.V.; Straub, J.E.; Thirumalai, D. Anisotropic coarse-grained statistical potentials improve the ability to identify nativelike protein structures. J. Chem. Phys. 2003, 118, 7658–7671. [Google Scholar] [CrossRef]
- Nanias, M.; Chinchio, M.; Ołdziej, S.; Czaplewski, C.; Scheraga, H. Protein structure prediction with the UNRES force-field using Replica-Exchange Monte Carlo-with-Minimization; Comparison with MCM, CSA, and CFMC. J. Comput. Chem. 2005, 26, 1472–1486. [Google Scholar] [CrossRef]
- Chu, J.W.; Voth, G. Allostery of actin filaments: Molecular dynamics simulations and coarse-grained analysis. Proc. Natl. Acad. Sci. USA 2005, 102, 13111–13116. [Google Scholar] [CrossRef]
- Neri, M.; Anselmi, C.; Cascella, M.; Maritan, A.; Carloni, P. Coarse-grained model of proteins incorporating atomistic detail of the active site. Phys. Rev. Lett. 2005, 95, 218102. [Google Scholar] [CrossRef]
- Brown, S.; Fawzi, N.J.; Head-Gordon, T. Coarse-grained sequences for protein folding and design. Proc. Natl. Acad. Sci. USA 2003, 100, 10712–10717. [Google Scholar] [CrossRef]
- Gohlke, H.; Thorpe, M. A Natural Coarse Graining for Simulating Large Biomolecular Motion. Biophys. J. 2006, 91, 2115–2120. [Google Scholar] [CrossRef]
- Haliloglu, T.; Bahar, I.; Erman, B. Gaussian Dynamics of Folded Proteins. Phys. Rev. Lett. 1997, 79, 3090–3093. [Google Scholar] [CrossRef]
- Tirion, M.M. Large amplitude elastic motions in proteins from a single-parameter, atomic analysis. Phys. Rev. Lett. 1996, 77, 1905–1908. [Google Scholar] [CrossRef] [PubMed]
- Ding, F.; Guo, W.; Dokholyan, N.V.; Shakhnovich, E.; Shea, J.E. Reconstruction of the src-SH3 protein domain transition state ensemble using multiscale molecular dynamics simulations. J. Mol. Biol. 2005, 350, 1035–1050. [Google Scholar] [CrossRef] [PubMed]
- Go, N. Theoretical studies of protein folding. Annu. Rev. Biophys. 1983, 12, 183–210. [Google Scholar]
- Ueda, Y.; Taketomi, H.; Go, N. Studies on protein folding, unfolding, and fluctuations by computer simulation. II. A. Three-dimensional lattice model of lysozyme. Biopolymers 1978, 17, 1531–1548. [Google Scholar] [CrossRef]
- Go¯, N.; Taketomi, H. Respective roles of short- and long-range interactions in protein folding. Proc. Natl. Acad. Sci. USA 1978, 75, 559–563. [Google Scholar] [CrossRef] [PubMed]
- Sikorski, A.; Skolnick, J. Monte Carlo simulation of equilibrium globular protein folding: α-helical bundles with long loops. Proc. Natl. Acad. Sci. USA 1989, 86, 2668–2672. [Google Scholar] [CrossRef]
- Skolnick, J.; Kolinski, A.; Yaris, R. Dynamic Monte Carlo Study of the Folding of a Six-Stranded Greek Key Globular Protein. Proc. Natl. Acad. Sci. USA 1989, 86, 1229–1233. [Google Scholar] [CrossRef]
- Honeycutt, J.D.; Thirumalai, D. Metastability of the folded states of globular proteins. Proc. Natl. Acad. Sci. USA 1990, 87, 3526–3529. [Google Scholar] [CrossRef]
- Jernigan, R.L.; Bahar, I. Structure-derived potentials and protein simulations. Curr. Opin. Struct. Biol. 1996, 6, 195–209. [Google Scholar] [CrossRef]
- Yue, K.; Dill, K.A. Forces of tertiary structural organization in globular proteins. Proc. Natl. Acad. Sci. USA 1995, 92, 146–150. [Google Scholar] [CrossRef] [PubMed]
- Ayton, G.S.; Noid, W.G.; Voth, G.A. Multiscale modeling of biomolecular systems: In serial and in parallel. Curr. Opin. Struct. Biol. 2007, 17, 192–198. [Google Scholar] [CrossRef] [PubMed]
- Nanias, M.; Czaplewski, C.; Scheraga, H.A. Replica exchange and multicanonical algorithms with the coarse-grained united-residue (UNRES) force field. J. Chem. Theory Comput. 2006, 2, 513–528. [Google Scholar] [CrossRef] [PubMed]
- Lau, K.F.; Dill, K.A. A lattice statistical mechanics model of the conformational and sequence spaces of proteins. Macromolecules 1989, 22, 3986–3997. [Google Scholar] [CrossRef]
- Tozzini, V. Coarse-grained models for proteins. Curr. Opin. Struct. Biol. 2005, 15, 144–150. [Google Scholar] [CrossRef]
- Berger, B.; Leighton, T. Protein Folding in the Hydrophobic-Hydrophilic (HP) Model is NP-Complete. J. Comput. Biol. 1998, 5, 27–40. [Google Scholar] [CrossRef]
- Halperin, A. Polymer Brushes that Resist Adsorption of Model Proteins: Design Parameters. Langmuir 1999, 15, 2525–2533. [Google Scholar] [CrossRef]
- Yang, C.H.; Wu, K.C.; Lin, Y.S.; Chuang, L.Y.; Chang, H.W. Protein folding prediction in the HP model using ions motion optimization with a greedy algorithm. BioData Min. 2018, 11, 17. [Google Scholar] [CrossRef]
- Bradley, R.; Radhakrishnan, R. Coarse-grained models for protein-cell membrane interactions. Polymers 2013, 5, 890–936. [Google Scholar] [CrossRef]
- Zhdanov, V.; Kasemo, B. Monte Carlo simulation of denaturation of adsorbed proteins. Proteins Struct. Funct. Genet. 1998, 30, 168–176. [Google Scholar] [CrossRef]
- Han, Y.; Cui, J.; Jin, J.; Jiang, W. Hydrogen bonding induced protein adsorption on polymer brushes: A Monte Carlo study. J. Mater. Chem. B 2017, 5, 8479–8486. [Google Scholar] [CrossRef] [PubMed]
- Dill, K.; Chan, H. From Levinthal to pathways to funnels. Nat. Struct. Mol. Biol. 1997, 4, 10–19. [Google Scholar] [CrossRef] [PubMed]
- Yue, K.; Fiebig, K.; Thomas, P.; Chan, H.; Shakhnovich, E.; Dill, K. A test of lattice protein folding algorithms. Proc. Natl. Acad. Sci. USA 1995, 92, 325–329. [Google Scholar] [CrossRef] [PubMed]
- Nie, Z.; Kumacheva, E. Patterning surfaces with functional polymers. Nat. Mater. 2008, 7, 277–290. [Google Scholar] [CrossRef]
- Anker, J.; Hall, W.; Lyandres, O.; Shah, N.; Zhao, J.; Duyne, R.V. Biosensing with plasmonic nanosensors. Nat. Mater. 2008, 7, 442–453. [Google Scholar] [CrossRef]
- Senaratne, W.; Andruzzi, L.; Ober, C.K. Self-Assembled Monolayers and Polymer Brushes in Biotechnology: Current Applications and Future Perspectives. Biomacromolecules 2005, 6, 2427–2448. [Google Scholar] [CrossRef]
- Stuart, M.A.C.; Huck, W.T.S.; Genzer, J.; Müller, M.; Ober, C.; Stamm, M.; Sukhorukov, G.B.; Szleifer, I.; Tsukruk, V.; Urban, M.; et al. Emerging applications of stimuli-responsive polymer materials. Nat. Mater. 2010, 9, 101–113. [Google Scholar] [CrossRef]
- Barbey, R.; Lavanant, L.; Paripovic, D.; Schüwer, N.; Sugnaux, C.; Tugulu, S.; Klok, H. Polymer brushes via surface-initiated controlled radical polymerization: Synthesis, characterization, properties, and applications. Chem. Rev. 2009, 109, 5437–5527. [Google Scholar] [CrossRef]
- Otsuka, H.; Nagasaki, Y.; Kataoka, K. PEGylated nanoparticles for biological and pharmaceutical applications. Adv. Drug Deliv. Rev. 2003, 55, 403–419. [Google Scholar] [CrossRef]
- Singh, M.K.; Ilg, P.; Espinosa-Marzal, R.M.; Kröger, M.; Spencer, N.D. Polymer Brushes under Shear: Molecular Dynamics Simulations Compared to Experiments. Langmuir 2015, 31, 4798–4805. [Google Scholar] [CrossRef]
- Yan, W.; Divandari, M.; Rosenboom, J.G.; Ramakrishna, S.N.; Trachsel, L.; Spencer, D.N.; Morgese, G.; Benetti, E.M. Design and characterization of ultrastablebiopassive and lubricious cyclic poly(2-alkyl-2-oxazoline) brushes. Polym. Chem. 2018, 9, 2580–2589. [Google Scholar] [CrossRef]
- Morgese, G.; Trachsel, L.; Romio, M.; Divandari, M.; Ramakrishna, S.N.; Benetti, E.M. Topological polymer chemistry enters surface science: Linear versus cyclic polymer brushes. Angew. Chem. Int. Ed. 2016, 55, 15583–15588. [Google Scholar] [CrossRef] [PubMed]
- Benetti, E.M. Quasi-3D-Structured Interfaces by Polymer Brushes. Macromol. Rapid Commun. 2018, 39, 1800189. [Google Scholar] [CrossRef] [PubMed]
- Binder, K.; Milchev, A. Polymer brushes on flat and curved surfaces: How computer simulations can help us to test theories and to interpret experiments. J. Polym. Sci. B 2012, 50, 1515–1555. [Google Scholar] [CrossRef]
- Kreer, T.; Metzger, S.; Müller, M.; Binder, K.; Baschnagel, J. Static properties of end-tethered polymers in good solution: A comparison between different models. J. Chem. Phys. 2004, 120, 4012–4023. [Google Scholar] [CrossRef]
- Zhao, B.; Brittain, W. Polymer brushes: Surface-immobilized macromolecules. Progr. Polym. Sci. 2000, 25, 677–710. [Google Scholar] [CrossRef]
- Jeyachandran, Y.L.; Mielczarski, E.; Rai, B.; Mielczarski, J.A. Quantitative and Qualitative Evaluation of Adsorption/Desorption of Bovine Serum Albumin on Hydrophilic and Hydrophobic Surfaces. Langmuir 2009, 25, 11614–11620. [Google Scholar] [CrossRef]
- O’Brien, C.; Stuart, S.; Bruce, D.; Latour, R. Modeling of peptide adsorption interactions with a poly(lactic acid) surface. Langmuir 2008, 24, 14115–14124. [Google Scholar] [CrossRef]
- Raffaini, G.; Ganazzoli, F. Understanding the Performance of Biomaterials through Molecular Modeling: Crossing the Bridge between their Intrinsic Properties and the Surface Adsorption of Proteins. Macromol. Biosci. 2007, 7, 552–566. [Google Scholar] [CrossRef]
- Wei, T.; Carignano, M.; Szleifer, I. Lysozyme adsorption on polyethylene surfaces: Why are long simulations needed? Langmuir 2011, 27, 12074–12081. [Google Scholar] [CrossRef]
- Qiu, R.; Xiao, J.; Chen, X.D. Multi-Peptide Adsorption on Uncharged Solid Surfaces: A Coarse-Grained Simulation Study. Engineering 2020, 6, 186–195. [Google Scholar] [CrossRef]
- Weeks, J.D.; Chandler, D.; Andersen, H. Role of repulsive forces in determining the equilibrium structure of simple liquids. J. Chem. Phys. 1971, 54, 5237. [Google Scholar] [CrossRef]
- Kröger, M. Simple models for complex nonequilibrium fluids. Phys. Rep. 2004, 390, 453–551. [Google Scholar] [CrossRef]
- van den Brule, B. Browian dynamics simulation of finitely extensible bead—Spring chains. J. Non-Newtonian Fluid Mech. 1993, 47, 357–378. [Google Scholar] [CrossRef]
- Kremer, K.; Grest, G.S. Dynamics of entangled linear polymer melts: A molecular-dynamics simulation. J. Chem. Phys. 1990, 92, 5057. [Google Scholar] [CrossRef]
- Kröger, M. Models for Polymeric and Anisotropic Liquids; Springer: Berlin/Heidelberg, Germany, 2005. [Google Scholar]
- Kröger, M. Simple, admissible, and accurate approximants of the inverse Langevin and Brillouin functions, relevant for strong polymer deformations and flows. J. Non-Newtonian Fluid Mech. 2015, 223, 77–87. [Google Scholar] [CrossRef]
- Kröger, M.; Loose, W.; Hess, S. Rheology and structural changes of polymer melts via nonequilibrium molecular dynamics. J. Rheol. 1993, 37, 1057–1079. [Google Scholar] [CrossRef]
- Cifre, J.G.H.; Hess, S.; Kröger, M. Linear viscoelastic behavior of unentangled polymer melts via nonequilibrium molecular dynamics. Macromol. Theory Simul. 2004, 13, 748–753. [Google Scholar] [CrossRef]
- Plimpton, S. Fast Parallel Algorithms for Short-Range Molecular Dynamics. J. Comp. Phys. 1995, 117, 1–19. [Google Scholar] [CrossRef]
- Berman, H.; Henrick, K.; Nakamura, H. Announcing the worldwide Protein Data Bank. Nat. Struct. Mol. Biol 2003, 980, 1545–9985. [Google Scholar] [CrossRef]
- Vojtechovsky, J.; Chu, K.; Berendzen, J.; Sweet, R.M.; Schlichting, I. Worldwide Protein Data Bank PDB Entry—1A6N. 1999. Available online: https://www.rcsb.org/structure/1a6n (accessed on 3 May 2023).
- Berg, J.M.; Tymoczko, J.L.; Stryer, L. Biochemistry; W.H. Freeman: Basingstoke, UK, 2012. [Google Scholar]
- Zhou, R.; Huang, X.; Margulis, C.J.; Berne, B.J. Hydrophobic Collapse in Multidomain Protein Folding. Science 2004, 305, 1605–1609. [Google Scholar] [CrossRef] [PubMed]
- Frömmel, C. The apolar surface area of amino acids and its empirical correlation with hydrophobic free energy. J. Theor. Biol. 1984, 111, 247–260. [Google Scholar] [CrossRef] [PubMed]
- The PyMOL Molecular Graphics System, Version 1.8; Schrödinger, LLC: New York, NY, USA, 2022.
- Pommié, C.; Levadoux, S.; Sabatier, R.; Lefranc, G.; Lefranc, M.P. IMGT standardized criteria for statistical analysis of immunoglobulin V-REGION aminoacid properties. J. Mol. Recognit. 2004, 17, 17–32. [Google Scholar] [CrossRef] [PubMed]
- Frauenfelder, H.; McMahon, B.H.; Fenimore, P.W. Myoglobin: The hydrogen atom of biology and a paradigm of complexity. Proc. Natl. Acad. Sci. USA 2003, 100, 8615–8617. [Google Scholar] [CrossRef]
- Lineback, J.E.; Jansma, A.L. PyMOL as an Instructional Tool To Represent and Manipulate the Myoglobin/Hemoglobin Protein System. J. Chem. Educ. 2019, 96, 2540–2544. [Google Scholar] [CrossRef]
- Miller, S.; Janin, J.; Lesk, A.M.; Chothia, C. Interior and surface of monomeric proteins. J. Mol. Biol. 1987, 196, 641–656. [Google Scholar] [CrossRef]
- Merlino, A.; Pontillo, N.; Graziano, G. A driving force for polypeptide and protein collapse. Phys. Chem. Chem. Phys. 2017, 19, 751–756. [Google Scholar] [CrossRef]
- Anfinsen, C. Principles that Govern the Folding of Protein Chains. Science 1973, 181, 223–230. [Google Scholar] [CrossRef]
- Halperin, A.; Kröger, M. Collapse of Thermoresponsive Brushes and the Tuning of Protein Adsorption. Macromolecules 2011, 44, 6986–7005. [Google Scholar] [CrossRef]
- Halperin, A.; Kröger, M. Theoretical considerations on mechanisms of harvesting cells cultured on thermoresponsive polymer brushes. Biomaterials 2012, 33, 4975–4987. [Google Scholar] [CrossRef]
- Yoshikawa, C.; Goto, A.; Tsujii, Y.; Fukuda, T.; Kimura, T.; Yamamoto, K.; Kishida, A. Protein Repellency of Well-Defined, Concentrated Poly(2-hydroxyethyl methacrylate) Brushes by the Size-Exclusion Effect. Macromolecules 2006, 39, 2284–2290. [Google Scholar] [CrossRef]
- Arkın, H.; Janke, W. Gyration tensor based analysis of the shapes of polymer chains in an attractive spherical cage. Chem. Phys. 2013, 138, 054904. [Google Scholar] [CrossRef] [PubMed]
- Alim, K.; Frey, E. Shapes of semiflexible polymer rings. Phys. Rev. Lett. 2007, 99, 198102. [Google Scholar] [CrossRef]
- Zifferer, G.; Olaj, O.F. Shape asymmetry of random walks and nonreversal random walks. Chem. Phys. 1994, 100, 636–639. [Google Scholar] [CrossRef]
- Rudnick, J.; Gaspari, G. The aspherity of random walks. J. Phys. A. Math. Gen. 1986, 19, L191. [Google Scholar] [CrossRef]
- Anfinsen, C.; Scheraga, H. Experimental and Theoretical Aspects of Protein Folding. Adv. Protein Chem. 1975, 29, 205–300. [Google Scholar]
- Privalov, P. Stability of Proteins Small Globular Proteins. Adv. Protein Chem. 1979, 33, 167–241. [Google Scholar] [PubMed]
- Izrailev, S.; Stepaniants, S.; Isralewitz, B.; Kosztin, D.; Lu, H.; Molnar, F.; Wriggers, W.; Schulten, K. Steered Molecular Dynamics. In Computational Molecular Dynamics: Challenges, Methods, Ideas, Proceedings of the 2nd International Symposium on Algorithms for Macromolecular Modelling, Berlin, Germany, 21–24 May 1997; Deuflhard, P., Hermans, J., Leimkuhler, B., Mark, A.E., Reich, S., Skeel, R.D., Eds.; Springer: Berlin/Heidelberg, Germany, 1999; pp. 39–65. [Google Scholar]
- Kumar, S.; Rosenberg, J.M.; Bouzida, D.; Swendsen, R.H.; Kollman, P.A. The weighted histogram analysis method for free-energy calculations on biomolecules. I. The method. J. Comput. Chem. 1992, 13, 1011–1021. [Google Scholar] [CrossRef]
- Sgouros, A.P.; Knippenberg, S.; Guillaume, M.; Theodorou, D.N. Multiscale simulations of polyzwitterions in aqueous bulk solutions and brush array configurations. Soft Matter 2021, 17, 10873–10890. [Google Scholar] [CrossRef]
- Korolev, N.; Luo, D.; Lyubartsev, A.P.; Nordenskioeld, L. A Coarse-Grained DNA Model Parameterized from Atomistic Simulations by Inverse Monte Carlo. Polymers 2014, 6, 1655–1675. [Google Scholar] [CrossRef]
- Tavanti, F.; Pedone, A.; Menziani, M. Multiscale Molecular Dynamics Simulation of Multiple Protein Adsorption on Gold Nanoparticles. Int. J. Mol. Sci. 2019, 20, 3539. [Google Scholar] [CrossRef] [PubMed]
- Vilaseca, P.; Dawson, K.A.; Franzese, G. Understanding and modulating the competitive surface-adsorption of proteins through coarse-grained molecular dynamics simulations. Soft Matter 2013, 9, 6978–6985. [Google Scholar] [CrossRef]
- Penna, M.J.; Mijajlovic, M.; Biggs, M.J. Molecular-Level Understanding of Protein Adsorption at the Interface between Water and a Strongly Interacting Uncharged Solid Surface. J. Am. Chem. Soc. 2014, 136, 5323–5331. [Google Scholar] [CrossRef] [PubMed]






















| R-Bead | w-Bead | H-Bead | P-Bead | A-Bead | Wall | Color | |
|---|---|---|---|---|---|---|---|
| R-bead | WCA | WCA | WCA | WCA | WCA | RW |  , , |
| w-bead | WCA | WCA | WCA | WCA | WCA | RW | — |
| H-bead | WCA | WCA | LJ | WCA | WCA | W |  |
| P-bead | WCA | WCA | WCA | WCA | LJ | LJ |  |
| A-bead | WCA | WCA | WCA | LJ | WCA | RW |  , , |
| Wall | W | W | W | W | W | W | W | W |
|---|---|---|---|---|---|---|---|---|
| color | purple | blue | light blue | green | light green | yellow | orange | red |
 |  |  |  |  |  |  |  | |
| I | 0.307 | 0.349 | 1.184 | 1.937 | 2.572 | 3.088 | 5.734 | 7.422 |
| Polymer Coating | N | G | R | |||||
|---|---|---|---|---|---|---|---|---|
| mushroom | 0.023 | 50 | 81 | 1.78 | 10.8 | 4.5 | 9.0 | 0.5 |
| intermediate | 0.056 | 50 | 196 | 4.31 | 12.1 | 4.7 | 10.5 | 1.3 |
| brush | 0.087 | 50 | 306 | 6.73 | 13.4 | 5.0 | 11.9 | 2.2 |
| Protein | hp | ||||
|---|---|---|---|---|---|
| S-protein | 25% | 40 | 24 | 1.9 | 2.9 |
| L-protein | 25% | 60 | 24 | 2.1 | 2.7 |
| S-protein | 35% | 40 | 24 | 1.9 | 3.1 |
| L-protein | 35% | 60 | 24 | 2.1 | 2.5 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Galata, A.A.; Kröger, M. Globular Proteins and Where to Find Them within a Polymer Brush—A Case Study. Polymers 2023, 15, 2407. https://doi.org/10.3390/polym15102407
Galata AA, Kröger M. Globular Proteins and Where to Find Them within a Polymer Brush—A Case Study. Polymers. 2023; 15(10):2407. https://doi.org/10.3390/polym15102407
Chicago/Turabian StyleGalata, Aikaterini A., and Martin Kröger. 2023. "Globular Proteins and Where to Find Them within a Polymer Brush—A Case Study" Polymers 15, no. 10: 2407. https://doi.org/10.3390/polym15102407
APA StyleGalata, A. A., & Kröger, M. (2023). Globular Proteins and Where to Find Them within a Polymer Brush—A Case Study. Polymers, 15(10), 2407. https://doi.org/10.3390/polym15102407