Research on Low-Velocity Impact Response of Novel Short-Fiber-Reinforced Composite Laminates
Abstract
:1. Introduction
2. Materials and Experimental Setup
2.1. Materials
2.2. Experimental Procedure
3. Finite Element Modeling
3.1. Johnson–Cook Elastic–Plastic Model
3.2. Damage Initiation Criterion
3.3. Damage Evolution Law
3.4. Interlaminar Damage
4. Results and Discussion
4.1. Impact Response
4.2. Post Impact C-Scan Inspection
4.3. Failure Modes Analysis
4.3.1. Fiber Tensile Damage
4.3.2. Matrix Tensile Damage and Compression Damage
4.3.3. Delamination of UACS Composite
5. Conclusions
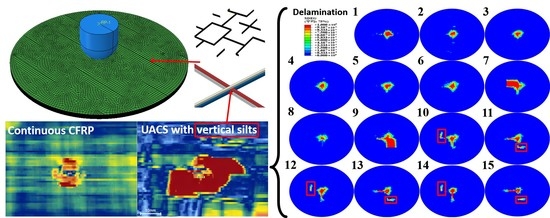
- At the same impact energy level, the UACS laminates with vertical slits show lower peak force than the continuous CFRP laminates. The continuous CFRP laminate shows a limited damage area, whereas the delamination of the UACS laminate offers the shape of a “vertical bar” in the vicinity of the slits, resulting in a larger damage area. With the increase in impact energy, the maximum displacement of UACS laminates is larger than that of continuous CFRP laminates and shows superior energy absorption capability.
- The finite element model is developed by the Johnson–Cook elastic–plastic model and PDM, and good accordance is determined between the numerical simulation and experimental measurements on the peak force of the laminates, as well as the maximum displacement and the energy absorbed during the impact event. Moreover, the effect of the dimension of slits, the stacking sequence and the thickness of laminates on the low-velocity impact performance of UACS laminates could be investigated further in future work.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Nomenclature | Fracture toughness for tensile damage of matrix | ||
| Fracture toughness for compressive damage of fiber | |||
| Symbol | definition | Fracture toughness for tensile damage of fiber | |
| Component stress acting at fiber direction | Hashin criteria for fiber failure in tension | ||
| Component stress acting at normal to the fiber | Hashin criteria for fiber failure in compression | ||
| Component stress acting at normal to the ply plane | Hashin criteria for matrix failure in tension | ||
| Shear stress acting at the ply plane | Hashin criteria for matrix failure in compression | ||
| Shear stress acting transverse to ply plane | Element characteristic length | ||
| Shear stress acting transverse to ply plane | Damage variable for fiber failure in tension | ||
| Static yield stress | Damage variable for fiber failure in compression | ||
| Young modulus at fiber direction | Damage variable for matrix failure in tension | ||
| Young modulus at normal to fiber | Damage variable for matrix failure in compression | ||
| Young modulus at normal to the ply plane | Material parameter of the BK fracture criterion | ||
| Shear modulus acting at the ply plane | Coefficients to manage the shear stiffness | ||
| Shear modulus acting at the ply plane | Coefficients to manage the shear stiffness | ||
| Shear modulus acting transverse to ply plane | Damage corresponding displacement of failure at initial failure | ||
| Poisson’s ratio acting at the ply plane | Damage corresponding displacement of failure at final failure | ||
| Poisson’s ratio acting at the ply plane | Elastic modulus of normal direction | ||
| Poisson’s ratio acting transverse to ply plane | Elastic modulus of shear direction | ||
| Fiber direction tensile strength | Elastic modulus of shear direction | ||
| Fiber direction compressive strength | Interface normal strength | ||
| Tensile strength in the cross sectional direction | Interface shear strength | ||
| Compressive strength in the cross sectional direction | Interface shear strength | ||
| Shear strength acting at the ply plane | Critical fracture energy of the normal direction | ||
| Shear strength acting at the ply plane | Critical fracture energy of the shear direction | ||
| Shear strength acting transverse to ply plane | Critical fracture energy of the total direction | ||
| Fracture toughness for compressive damage of matrix | Equivalent plastic strain | ||
References
- Zhang, X. Impact on Composite Structures. In The Aeronautical Journal; Abrate, S., Ed.; Cambridge University Press: Cambridge, UK, 1998; Volume 103, p. 536. ISBN 0521473896. [Google Scholar] [CrossRef]
- Zhang, H.; Liu, M. Development and Applications of Carbon Fiber Reinforced Polymer. Eng. Plast. Appl. 2015, 43, 132–135. [Google Scholar]
- Friedrich, K.; Almajid, A.A. Manufacturing aspects of advanced polymer composites for automotive applications. Appl. Compos. Mater. 2013, 20, 107–128. [Google Scholar] [CrossRef]
- Palmer, J.S.L.; Ghita, O.R.; Evans, K.E. Sheet moulding compound (SMC) from carbon fibre recyclate. Compos. Part A Appl. Sci. Manuf. 2010, 41, 1232–1237. [Google Scholar] [CrossRef]
- Thomason, J.L. The influence of fibre length and concentration on the properties of glass fibre reinforced polypropylene: 7. Interface strength and fibre strain in injection moulded long fibre PP at high fibre content. Compos. Part A Appl. Sci. Manuf. 2007, 38, 210–216. [Google Scholar] [CrossRef]
- Taketa, I.; Okabe, T.; Kitano, A. A new compression-molding approach using unidirectionally arrayed chopped strands. Compos. Part A Appl. Sci. Manuf. 2008, 39, 1884–1890. [Google Scholar] [CrossRef]
- Li, H.; Wang, W.-X.; Takao, Y.; Matsubara, T. New designs of unidirectionally arrayed chopped strands by introducing discontinuous angled slits into prepreg. Compos. Part A Appl. Sci. Manuf. 2013, 45, 127–133. [Google Scholar] [CrossRef]
- Richardson, M.O.W.; Wisheart, M.J. Review of low-velocity impact properties of composite materials. Compos. Part A Appl. Sci. Manuf. 1996, 27, 1123–1131. [Google Scholar] [CrossRef]
- Shah, S.Z.H.; Karuppanan, S.; Megat-Yusoff, P.S.M.; Sajid, Z. Impact resistance and damage tolerance of fiber reinforced composites: A review. Compos. Struct. 2019, 217, 100–121. [Google Scholar] [CrossRef]
- Kim, E.-H.; Rim, M.-S.; Lee, I.; Hwang, T.-K. Composite damage model based on continuum damage mechanics and low velocity impact analysis of composite plates. Compos. Struct. 2013, 95, 123–134. [Google Scholar] [CrossRef]
- Shivakumar, K.; Elber, W.; Illg, W. Prediction of low-velocity impact damage in thin circular laminates. AIAA J. 1985, 23, 442–449. [Google Scholar] [CrossRef]
- Mathivanan, N.R.; Jerald, J.J. Experimental investigation of low-velocity impact characteristics of woven glass fiber epoxy matrix composite laminates of EP3 grade. Mater. Des. 2010, 31, 4553–4560. [Google Scholar] [CrossRef]
- Ibrahim, G.R.; Albarbar, A.; Brethee, K.F. Damage degradation modelling for transverse cracking in composite laminates under low-velocity impact. Eng. Fract. Mech. 2022, 263, 108286. [Google Scholar] [CrossRef]
- Mishra, A.; Naik, N.K. Failure initiation in composite structures under low-velocity impact: Analytical studies. Compos. Struct. 2010, 92, 436–444. [Google Scholar] [CrossRef]
- Xiao, S.; Chen, P.; Ye, Q. Prediction of damage area in laminated composite plates subjected to low velocity impact. Compos. Sci. Technol. 2014, 98, 51–56. [Google Scholar] [CrossRef]
- Olsson, R. Analytical prediction of damage due to large mass impact on thin ply composites. Compos. Part A Appl. Sci. Manuf. 2015, 72, 184–191. [Google Scholar] [CrossRef]
- Bui, T.Q.; Hirose, S.; Zhang, C.; Rabczuk, T.; Wu, C.-T.; Saitoh, T.; Lei, J. Extended isogeometric analysis for dynamic fracture in multiphase piezoelectric/piezomagnetic composites. Mech. Mater. 2016, 97, 135–163. [Google Scholar] [CrossRef]
- Singh, H.; Mahajan, P. Analytical modeling of low velocity large mass impact on composite plate including damage evolution. Compos. Struct. 2016, 149, 79–92. [Google Scholar] [CrossRef]
- Yu, Z.; Gao, S. Increase of contact radius due to deflection in low velocity impact of composite laminates and prediction of delamination threshold load. Compos. Struct. 2016, 147, 286–293. [Google Scholar] [CrossRef]
- Demiral, M.; Abbassi, F.; Saracyakupoglu, T.; Habibi, M. Damage analysis of a CFRP cross-ply laminate subjected to abrasive water jet cutting. Alex. Eng. J. 2022, 61, 7669–7684. [Google Scholar] [CrossRef]
- Demiral, M.; Kadioglu, F.; Silberschmidt, V.V. Size effect in flexural behaviour of unidirectional GFRP composites. J. Mech. Sci. Technol. 2020, 34, 5053–5061. [Google Scholar] [CrossRef]
- Zhou, J.; Wen, P.; Wang, S. Finite element analysis of a modified progressive damage model for composite laminates under low-velocity impact. Compos. Struct. 2019, 225, 111113. [Google Scholar] [CrossRef]
- Feng, D.; Aymerich, F. Finite element modelling of damage induced by low-velocity impact on composite laminates. Compos. Struct. 2014, 108, 161–171. [Google Scholar] [CrossRef]
- Krueger, R. Virtual crack closure technique: History, approach, and applications. Appl. Mech. Rev. 2004, 57, 109–143. [Google Scholar] [CrossRef]
- Camanho, P.P.; Davila, C.G.; de Moura, M.F. Numerical simulation of mixed-mode progressive delamination in composite materials. J. Compos. Mater. 2003, 37, 1415–1438. [Google Scholar]
- Hou, J.P.; Petrinic, N.; Ruiz, C.; Hallett, S.R. Prediction of impact damage in composite plates. Compos. Sci. Technol. 2000, 60, 273–281. [Google Scholar] [CrossRef]
- Li, X.; Hallett, S.R.; Wisnom, M.R. Predicting the effect of through-thickness compressive stress on delamination using interface elements. Compos. Part A Appl. Sci. Manuf. 2008, 39, 218–230. [Google Scholar] [CrossRef]
- Zhang, X.; Bianchi, F.; Liu, H. Predicting low-velocity impact damage in composites by a quasi-static load model with cohesive interface elements. Aeronaut. J. 2012, 116, 1367–1381. [Google Scholar] [CrossRef]
- Zhang, J.; Zhang, X. Simulating low-velocity impact induced delamination in composites by a quasi-static load model with surface-based cohesive contact. Compos. Struct. 2015, 125, 51–57. [Google Scholar] [CrossRef]
- Shi, Y.; Pinna, C.; Soutis, C. Modelling impact damage in composite laminates: A simulation of intra- and inter-laminar cracking. Compos. Struct. 2014, 114, 10–19. [Google Scholar] [CrossRef]
- Falcó, O.; Lopes, C.S.; Sommer, D.E.; Thomson, D.; Ávila, R.; Tijs, B. Experimental analysis and simulation of low-velocity impact damage of composite laminates. Compos. Struct. 2022, 287, 115278. [Google Scholar] [CrossRef]
- Hu, J.; Zhang, X.; Chen, Z.; Guo, W.; Li, H.; Deng, X. Experimental and Numerical Research on Open-Hole Strength and Damage Mechanism of Regularly Arrayed Short Fiber Reinforced Polymer Composite. Polymers 2020, 12, 1622. [Google Scholar] [CrossRef]
- Liu, P.F.; Liao, B.B.; Jia, L.Y.; Peng, X.Q. Finite element analysis of dynamic progressive failure of carbon fiber composite laminates under low velocity impact. Compos. Struct. 2016, 149, 408–422. [Google Scholar] [CrossRef]
- Li, X.; Ma, D.; Liu, H.; Tan, W.; Gong, X.; Zhang, C.; Li, Y. Assessment of failure criteria and damage evolution methods for composite laminates under low-velocity impact. Compos. Struct. 2019, 207, 727–739. [Google Scholar] [CrossRef]
- Xin, S.H.; Wen, H.M. A progressive damage model for fiber reinforced plastic composites subjected to impact loading. Int. J. Impact Eng. 2015, 75, 40–52. [Google Scholar] [CrossRef]
- Fuller, J.D.; Wisnom, M.R. Pseudo-ductility and damage suppression in thin ply CFRP angle-ply laminates. Compos. Part A Appl. Sci. Manuf. 2015, 69, 64–71. [Google Scholar] [CrossRef]
- Hashin, Z.; Rotem, A. A Fatigue Failure Criterion for Fiber Reinforced Materials. J. Compos. Mater. 1973, 7, 448–464. [Google Scholar] [CrossRef]
- Zhang, C.; Li, N.; Wang, W.; Binienda, W.K.; Fang, H. Progressive damage simulation of triaxially braided composite using a 3D meso-scale finite element model. Compos. Struct. 2015, 125, 104–116. [Google Scholar] [CrossRef]
- Benzeggagh, M.L.; Kenane, M. Measurement of mixed-mode delamination fracture toughness of unidirectional glass/epoxy composites with mixed-mode bending apparatus. Compos. Sci. Technol. 1996, 56, 439–449. [Google Scholar] [CrossRef]

















| Parameters | Value |
|---|---|
| Density | 1600 kg/m3 |
| Stiffness properties | = 145 Gpa, = = 9 Gpa, = = 4.4 Gpa, = 3.7 Gpa, = = 0.3, = 0.4 |
| Strength properties | = 2600 Mpa, = 1050 Mpa, = 62 Mpa, = 192 Mpa, = = 90 Mpa, = 52 MPa |
| Fracture Energy | = 82 N/mm, = 70 N/mm, = 0.22 N/mm, = 1.1 N/mm |
| Parameters | Value |
|---|---|
| Elastic modulus | = = = 5 GPa/mm |
| Strength properties | N = S = T = 30 MPa |
| Fracture energy | = 0.32 N/mm; = 1 N/mm |
| Relevant coefficient |
| Specimen | Impact Energy (J) | Peak Force (kN) | Maximum Displacement (mm) | Absorbed Energy (J) | Damage Area (mm2) |
|---|---|---|---|---|---|
| CFRP | 4 | 2.33 ± 0.08 | 3.51 ± 0.18 | 1.89 ± 0.03 | 153 ± 14.50 |
| 7 | 3.35 ± 0.11 | 4.49 ± 0.23 | 3.19 ± 0.13 | 250.5 ± 25.25 | |
| 11 | 4.56 ± 0.21 | 5.53 ± 0.46 | 5.24 ± 0.08 | 311 ± 22.05 | |
| UACS | 4 | 1.97 ± 0.09 | 4.18 ± 0.30 | 2.31 ± 0.08 | 485.75 ± 41.75 |
| 7 | 2.13 ± 0.15 | 6.86 ± 0.58 | 6.05 ± 0.38 | 889.75 ± 56.05 | |
| 11 | 1.46 ± 0.11 | 10.79 ± 0.71 | 10.38 ± 0.24 | 1230 ± 87.85 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, Y.; EShun, F.T.; Hu, J.; Zhang, X.; Zhao, J.; Zhang, S.; Qian, R.; Chen, Z.; Chen, D. Research on Low-Velocity Impact Response of Novel Short-Fiber-Reinforced Composite Laminates. Polymers 2023, 15, 840. https://doi.org/10.3390/polym15040840
Huang Y, EShun FT, Hu J, Zhang X, Zhao J, Zhang S, Qian R, Chen Z, Chen D. Research on Low-Velocity Impact Response of Novel Short-Fiber-Reinforced Composite Laminates. Polymers. 2023; 15(4):840. https://doi.org/10.3390/polym15040840
Chicago/Turabian StyleHuang, Yinyuan, Felix Thompson EShun, Junfeng Hu, Xutong Zhang, Jianping Zhao, Siqi Zhang, Rui Qian, Zhou Chen, and Dingding Chen. 2023. "Research on Low-Velocity Impact Response of Novel Short-Fiber-Reinforced Composite Laminates" Polymers 15, no. 4: 840. https://doi.org/10.3390/polym15040840
APA StyleHuang, Y., EShun, F. T., Hu, J., Zhang, X., Zhao, J., Zhang, S., Qian, R., Chen, Z., & Chen, D. (2023). Research on Low-Velocity Impact Response of Novel Short-Fiber-Reinforced Composite Laminates. Polymers, 15(4), 840. https://doi.org/10.3390/polym15040840