Optimization for the Contrary-Rotating Double-Screw Extrusion of Plastics
Abstract
:1. Introduction
- -
- Optimization variables are coded;
- -
- Searching for a solution starts from some population, which means the probability of getting stuck at a local extreme is low;
- -
- The rules of selection are probabilistic;
- -
- Objective functions are used, and derivatives are not necessary.
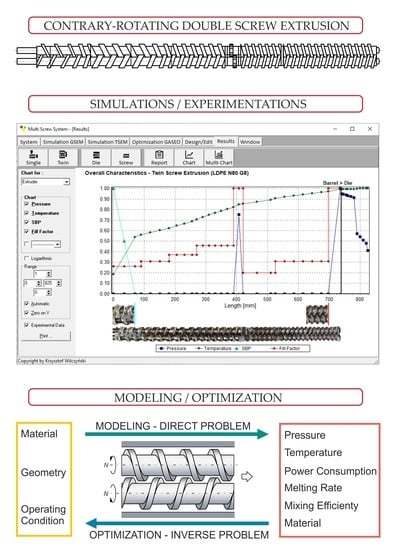
2. Contrary-Rotating Double-Screw Extrusion
3. Modeling of Contrary-Rotating Double-Screw Extrusion
4. Optimization Procedure
5. Optimization
5.1. Research Program
5.2. Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Underwood, W.M. Experimental Method for Designing Extrusion Screws. Chem. Eng. Prog. 1962, 58, 59. [Google Scholar]
- Verbraak, C.P.J.M.; Meijer, H.E.H. Screw Design in Injection Molding. Polym. Eng. Sci. 1989, 29, 479–487. [Google Scholar] [CrossRef]
- Tadmor, Z.; Klein, I. Engineering Principles of Plasticating Extrusion; Van Nostrand Reinhold Co.: New York, NY, USA, 1970; ISBN 978-044-215-635-0. [Google Scholar]
- Maddock, B.H.; Smith, D.J. Extruder Design by Computer Printout. SPE J. 1972, 28, 12–17. [Google Scholar]
- Helmy, H.A.A.; Parnaby, J. Computer—Aided Optimal Melt Screw Design. Polym. Eng. Sci. 1976, 16, 437–449. [Google Scholar] [CrossRef]
- Potente, H.; Krell, B. Screw optimization by means of DOE and multiple regression. In Proceedings of the 55th Annual Technical Conferences of the Society of Plastics Engineers (ANTEC 1997), Toronto, ON, Canada, 27 April–2 May 1997; pp. 135–139. [Google Scholar]
- Potente, H.; Hanhart, W.; Schöppner, V. Potential Applications for Computer-aided Extruder Design. Int. Polym. Process. 1993, 8, 335–344. [Google Scholar] [CrossRef]
- Potente, H.; Hanhart, W.; Reski, T. Design and Processing Optimization of Extruder Screws. Polym. Eng. Sci. 1994, 34, 937–945. [Google Scholar] [CrossRef]
- Potente, H.; Schöppner, V.; Ujma, A. Successful Simulation of Wall—Slipping Plastics. J. Polym. Eng. 1997, 17, 153–170. [Google Scholar] [CrossRef]
- Thibodeau, C.A.; Lafleur, P.G. Computer Design and Screw Optimization. In Proceedings of the 58th Annual Technical Conference of the Society of Plastics Engineers (ANTEC 2000), Orlando, FL, USA, 7–11 May 2000; pp. 276–282. [Google Scholar]
- Thibodeau, C.A.; Lafleur, P.G. Computer Design and Screw Optimization. In Proceedings of the Polymer Processing Society 16th Annual Meeting (PPS-16), Shanghai, China, 18–23 June 2000; p. 15. [Google Scholar]
- Amellal, K.; Lafleur, P.G. Computer Simulation of Conventional and Barrier Screw Extruders. Plast. Rub. Compos. Pro. 1993, 19, 227–239. [Google Scholar]
- Vincelette, A.R.; Guerrero, C.S.; Carreau, P.J.; Lafleur, P.G. A Model for Single-Screw Plasticating Extruders. Int. Polym. Process. 1989, 4, 232–241. [Google Scholar] [CrossRef]
- Covas, J.A.; Cunha, A.G.; Oliveira, P. An Optimization Approach to Practical Problems in Plasticating Single Screw Extrusion. Polym. Eng. Sci. 1999, 39, 443–456. [Google Scholar] [CrossRef]
- Covas, J.A.; Gaspar-Cunha, A. The Use of an Optimization Approach to the Design of Extrusion Screw. In Proceedings of the Polymer Processing Society 16th Annual Meeting (PPS-16), Shanghai, China, 18–23 June 2000. [Google Scholar]
- Gaspar-Cunha, A.; Covas, J.A. The Design of Extrusion Screw: An Optimization Approach. Int. Polym. Process. 2001, 16, 229–240. [Google Scholar] [CrossRef] [Green Version]
- Gaspar-Cunha, A.; Covas, J.A.; Vergnes, B. An Optimization Methodology for Setting the Operating Conditions in Twin-Screw Extrusion. In Proceedings of the Polymer Processing Society 18th Annual Meeting (PPS-18), Guimaraes, Portugal, 18–21 June 2002. [Google Scholar]
- Gaspar-Cunha, A.; Poulesquen, A.; Vergnes, B.; Covas, J.A. Optimization of Processing Conditions for Polymer Twin-Screw Extrusion. Int. Polym. Process. 2002, 17, 201–213. [Google Scholar] [CrossRef]
- Gaspar-Cunha, A.; Covas, J.; Vergnes, B. Defining the Configuration of Co-Rotating Twin-Screw Extruders with Multiobjective Evolutionary Algorithms. Polym. Eng. Sci. 2005, 45, 1159–1173. [Google Scholar] [CrossRef]
- Nastaj, A.; Wilczyński, K. Process Optimization for Single Screw Extrusion of Polymeric Materials—Simulation Studies. Polimery 2018, 4, 297–304. [Google Scholar] [CrossRef]
- Covas, J.A.; Gaspar-Cunha, A. Extrusion Scale-up: An Optimization-based Methodology. Int. Polym. Process. 2009, 24, 67–82. [Google Scholar] [CrossRef]
- Covas, J.A.; Gaspar-Cunha, A. A Scaling-up Methodology for Co-rotating Twin-Extruders. In Proceedings of the 27th Annual Meeting of the Polymer Processing Society (PPS-27), Marrakesh, Morocco, 10–14 May 2011; pp. 1–6. [Google Scholar]
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Gaspar-Cunha, A. Using Multiobjective Evolutionary Algorithms in the Optimization of Operating Conditions of Polymer Injection Molding. Polym. Eng. Sci. 2010, 50, 1667–1678. [Google Scholar] [CrossRef]
- Fernandes, C.; Pontes, A.J.; Viana, J.C.; Gaspar-Cunha, A. Using Multi-objective Evolutionary Algorithms for Optimization of the Cooling System in Polymer Injection Molding. Int. Polym. Process. 2012, 27, 213–223. [Google Scholar] [CrossRef] [Green Version]
- Nastaj, A.; Wilczyński, K. Optimization for Starve Fed/Flood Fed Single Screw Extrusion of Polymeric Materials. Polymers 2020, 12, 149. [Google Scholar] [CrossRef] [Green Version]
- Nastaj, A.; Wilczyński, K. Optimization and Scale-Up for Polymer Extrusion. Polymers 2021, 13, 1547. [Google Scholar] [CrossRef] [PubMed]
- Wilczyński, K.J.; Nastaj, A.; Lewandowski, A.; Wilczyński, K. A Composite Model for Starve Fed Single Screw Extrusion of Thermoplastics. Polym. Eng. Sci. 2014, 54, 2362–2374. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Lewandowski, A.; Nastaj, A.; Wilczyński, K. Modeling for Starve Fed/Flood Fed Mixing Single-Screw Extruders. Int. Polym. Process. 2016, 31, 82–91. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Lewandowski, A.; Nastaj, A.; Wilczyński, K. A Global Model for Starve-Fed Nonconventional Single-Screw Extrusion of Thermoplastics. Adv. Polym. Technol. 2017, 36, 23–35. [Google Scholar] [CrossRef]
- Wilczyński, K.J.; Nastaj, A.; Wilczyński, K. A Computer Model for Starve-Fed Single-Screw Extrusion of Polymer Blends. Adv. Polym. Technol. 2018, 37, 2142–2151. [Google Scholar] [CrossRef]
- Wilczyński, K.; Jiang, Q.; White, J.L. A Composite Model for Melting, Pressure and Fill Factor Profiles in a Metered Fed Closely Intermeshing Counter-Rotating Twin Screw Extruder. Int. Polym. Process. 2007, 22, 198–203. [Google Scholar] [CrossRef]
- Wilczyński, K.; Lewandowski, A. Study on the Polymer Melt Flow in a Closely Intermeshing Counter-Rotating Twin Screw Extruder. Int. Polym. Process. 2014, 29, 649–659. [Google Scholar] [CrossRef]
- Lewandowski, A.; Wilczyński, K.J.; Nastaj, A.; Wilczyński, K. A Composite Model for an Intermeshing Counter-Rotating Twin-Screw Extruder and its Experimental Verification. Polym. Eng. Sci. 2015, 55, 2838–2848. [Google Scholar] [CrossRef]
- Wilczyński, K. Rheology in Polymer Processing. Modeling and Simulation; Carl Hanser Verlag: Munich, Germany, 2021; ISBN 978-1-56990-660-6. [Google Scholar]
- Rauwendaal, C. Polymer Extrusion, 5th ed.; Carl Hanser Verlag: Munich, Germany, 2014; ISBN 978-1-56990-516-6. [Google Scholar]
- White, J.L.; Potente, H. Screw Extrusion. Science and Technology; Hanser Publishers: Munich, Germany, 2003; ISBN 978-3-446-19624-7. [Google Scholar]
- Tadmor, Z.; Gogos, C.G. Principles of Polymer Processing, 2nd ed.; John Wiley & Sons Inc.: New York, NY, USA, 2006; ISBN 978-0-471-38770-1. [Google Scholar]
- Osswald, T.; Hernandez-Ortiz, J.P. Polymer Processing. Modeling and Simulation; Carl Hanser Verlag: Munich, Germany, 2006; ISBN 978-3-446-40381-9. [Google Scholar]
- Agassant, J.F.; Avenas, P.; Carreau, P.J.; Vergnes, B.; Vincent, M. Polymer Processing. Principles and Modelling, 2nd ed.; Carl Hanser Verlag: Munich, Germany, 2017; ISBN 978-1-56990-605-7. [Google Scholar]
- Altinkaynak, A.; Gupta, M.; Spalding, M.A.; Crabtree, S.L. Melting in a Single Screw Extruder: Experiments and 3D Finite Element Simulations. Int. Polym. Process. 2011, 26, 182–196. [Google Scholar] [CrossRef]
- Ariffin, A.; Ahmad, M.S.B. Review: Single Screw Extruder in Particulate Filler Composite. Polym.-Plast. Technol. 2011, 50, 395–403. [Google Scholar] [CrossRef]
- Teixeira, C.; Gaspar-Cunha, A.; Covas, J.A. Flow and Heat Transfer Along the Length of a Co-rotating Twin Screw Extruder. Polym.-Plast. Technol. 2012, 51, 1567–1577. [Google Scholar] [CrossRef]
- Malik, M.; Kalyon, D.M.; Golba, J.C., Jr. Simulation of Co-Rotating Twin Screw Extrusion Process Subject to Pressure-Dependent Wall Slip at Barrel and Screw Surfaces: 3D FEM Analysis for Combinations of Forward- and Reverse-Conveying Screw Elements. Int. Polym. Process. 2014, 29, 51–62. [Google Scholar] [CrossRef]
- Wilczyński, K.; Nastaj, A.; Lewandowski, A.; Wilczyński, K.J.; Buziak, K. Fundamentals of Global Modeling for Polymer Extrusion. Polymers 2019, 11, 2106. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Leistritz, P.; Burghauser, F. German Patent. 1927, 453, 727.
- Kiesskalt, S. Untersuchungen an einer Kapsel Pumpe. VDI Z. 1927, 71, 453. [Google Scholar]
- Montelius, C.O.J. U.S. Patent. 1929, 1, 802.
- Montelius, C.O.J. Der Kogelige Danske Videnscabernes Selscabs Skrifter. Tek. Tidskr. 1933, 6, 61–63. [Google Scholar]
- Schenkel, G. Kunststoffe Extrudertechnik; Hanser: Munich, Germany, 1963. [Google Scholar]
- White, J.L. Twin Screw Extrusion. Technology and Principles; Hanser: Munich, Germany, 1990. [Google Scholar]
- Doboczky, Z. Theoretische and wirkliche Ausstoßleistung der Doppelschnecken Extruder. Plastverarbeiter 1965, 19, 395–400. [Google Scholar]
- Janssen, L.P.B.M. Twin Screw Extrusion; Elsevier: Amsterdam, The Netherlands, 1978. [Google Scholar]
- White, J.L.; Adewale, A. A Unified View of Modeling Flow in Counter-rotating Twin Screw Extruders. Int. Polym. Process. 1993, 8, 210–217. [Google Scholar] [CrossRef]
- Li, T.; Manas Zloczower, I. Flow Field Analysis of an Intermeshing Counter-Rotating Twin Screw Extruder. Polym. Eng. Sci. 1994, 34, 551–558. [Google Scholar] [CrossRef]
- Kajiwara, T.; Nagashima, Y.; Naakano, Y.; Funatsu, K. Numerical Study of Twin Screw Extruders by ThreeDimensional Flow Analysis—Development of Analysis Technique and Evaluation of Mixing Performance for Full Flight Screws. Polym. Eng. Sci. 1996, 36, 2142–2152. [Google Scholar] [CrossRef]
- Hong, M.H.; White, J.L. Fluid Mechanics of Intermeshing Counter-Rotating Twin Screw Extruders. Int. Polym. Process. 1998, 13, 342–346. [Google Scholar] [CrossRef]
- Hong, M.H.; White, J.L. Simulation of Flow in an Intermeshing Modular Counter-Rotating Twin Screw Extruder: Non-Newtonian and Non-Isothermal Behavior. Int. Polym. Process. 1999, 14, 136–143. [Google Scholar] [CrossRef]
- Wilczyński, K.; White, J.L. Experimental Study of Melting in an Intermeshing Counter-Rotating Twin Screw Extruder. Int. Polym. Process. 2001, 16, 257–262. [Google Scholar] [CrossRef]
- Wilczyński, K.; White, J.L. Melting Model for Intermeshing Counter-Rotating Twin-Screw Extruders. Polym. Eng. Sci. 2003, 43, 1715–1726. [Google Scholar] [CrossRef]
- Wang, D.; Min, K. In-Line Monitoring and Analysis of Polymer Melting Behavior in an Intermeshing Counter-Rotating Twin-Screw Extruder by Ultrasound Waves. Polym. Eng. Sci. 2005, 45, 998–1010. [Google Scholar] [CrossRef]
- Wang, D.; Min, K. Experiments and Analysis of Effect of Calender Gaps on Melting of PVC Powders in an Intermeshing Counter-Rotating Twin-Screw Extruder. Int. Polym. Process. 2006, 21, 17–23. [Google Scholar] [CrossRef]
- Wilczyński, K.; Lewandowski, A.; Wilczyński, K.J. Experimental Study of Melting of LDPE/PS Polyblend in an Intermeshing Counter-Rotating Twin Screw Extruder. Polym. Eng. Sci. 2012, 52, 449–458. [Google Scholar] [CrossRef]
- Jiang, Q.; White, J.L.; Yang, J. A Global Model for Closely Intermeshing Counter-Rotating Twin Screw Extruders with Flood Feeding. Int. Polym. Process. 2010, 25, 223–235. [Google Scholar] [CrossRef]



















| Screw Rotation N, rpm | Cylinder Temperature TI, °C | Cylinder Temperature TII, °C | Cylinder Temperature TIII, °C | Cylinder Temperature TIV, °C | Extrusion Output Q, kg/h |
|---|---|---|---|---|---|
| 40 ÷ 240 | 180 | 180 ÷ 240 | 180 ÷ 240 | 180 ÷ 240 | 1 ÷ 100 |
| Criterion Weights | ||||||
|---|---|---|---|---|---|---|
| wQ = 0.8 wTout = 0.1 wLpl = 0.1 | wQ = 0.1 wTout = 0.8 wLpl = 0.1 | wQ = 0.1 wTout = 0.1 wLpl = 0.8 | wQ = 0.4 wTout = 0.4 wLpl = 0.2 | wQ = 0.4 wTout = 0.2 wLpl = 0.4 | wQ = 0.2 wTout = 0.4 wLpl = 0.4 | |
| No | 1 | 2 | 3 | 4 | 5 | 6 |
| Screw rotation N, rpm | 227.5 | 227.5 | 152.5 | 227.5 | 240 | 96.3 |
| Cylinder temperature TII, °C | 180 | 180 | 219.4 | 180 | 180 | 196.9 |
| Cylinder temperature TIII, °C | 180 | 180 | 219.4 | 180 | 180 | 180 |
| Cylinder temperature TIV, °C | 187.5 | 180 | 230.6 | 180 | 187.5 | 187.5 |
| Extrusion throughput Q, kg/h | 65.63 | 62.50 | 9.38 | 65.63 | 65.63 | 12.50 |
| Temperature of plastic at die outlet Tout, °C | 176.25 | 181.49 | 206.42 | 175.75 | 181.58 | 197.24 |
| Length of plastic melting Lpl, mm | 960 | 920 | 160 | 960 | 920 | 240 |
| Objective function Fi | 0.6243 | 0.8563 | 0.8373 | 0.6673 | 0.4934 | 0.5819 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nastaj, A.; Wilczyński, K. Optimization for the Contrary-Rotating Double-Screw Extrusion of Plastics. Polymers 2023, 15, 1489. https://doi.org/10.3390/polym15061489
Nastaj A, Wilczyński K. Optimization for the Contrary-Rotating Double-Screw Extrusion of Plastics. Polymers. 2023; 15(6):1489. https://doi.org/10.3390/polym15061489
Chicago/Turabian StyleNastaj, Andrzej, and Krzysztof Wilczyński. 2023. "Optimization for the Contrary-Rotating Double-Screw Extrusion of Plastics" Polymers 15, no. 6: 1489. https://doi.org/10.3390/polym15061489
APA StyleNastaj, A., & Wilczyński, K. (2023). Optimization for the Contrary-Rotating Double-Screw Extrusion of Plastics. Polymers, 15(6), 1489. https://doi.org/10.3390/polym15061489