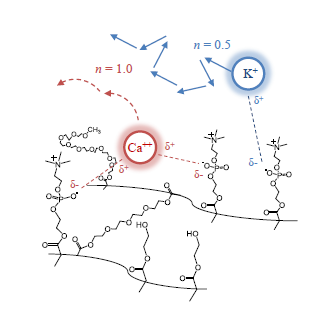
Polyplex Formation Influences Release Mechanism of Mono- and Di-Valent Ions from Phosphorylcholine Group Bearing Hydrogels
Abstract
:1. Introduction
| Slab | Cylinder * | Sphere | Release Mechanism |
|---|---|---|---|
| 0.5 | 0.43 | 0.43 | Fickian |
| 0.5 < n < 1.0 | 0.43 < n < 0.89 | 0.43 < n < 0.85 | Anomalous |
| 1.0 | 0.89 | 0.85 | Case II |
2. Experimental Section
2.1. Reagents
2.2. Preparation of Monomer Cocktail and Synthesis of Hydrogel Discs
| Hydrogel Constituent | Mol Percent of Hydrogel (%) |
|---|---|
| HEMA | 90.0 |
| TEGDA | 3.0 |
| PEG(400)MA | 5.0 * |
| MPC | 1.0 |
| DMPA | 1.0 |

2.3. Experimental Setup for Release of Charged Species [27]
2.4. Calibration and Performance of ISEs
2.5. Hydrogel Characterization
2.6. Analysis of Release Profiles
3. Results and Discussion
3.1. Release Profiles

3.2. Cation Effects on Release and Polymer Structure

| Nested ANOVA for Diffusional Exponent (n) | ||||||
|---|---|---|---|---|---|---|
| Source | SS | d.f. | MS | F | p | |
| Loading | 0.2371 | 1 | 0.2371 | 3.12 | 0.0970 | |
| Ion | 3.1399 | 1 | 3.1399 | 41.28 | 0.0000 | |
| Temp (Loading, Ion) | 1.0551 | 13 | 0.0812 | 1.74 | 0.0634 | |
| Error | 4.5592 | 98 | 0.0465 | |||
| Total | 8.7794 | 113 | ||||
| Nested ANOVA for Rate Constat (kkp) | ||||||
| Source | SS | d.f. | MS | F | p | |
| Loading | 0.0012 | 1 | 0.0012 | 0.18 | 0.6739 | |
| Ion | 0.1763 | 1 | 0.1763 | 28.23 | 0.0001 | |
| Temp (Loading, Ion) | 0.0892 | 13 | 0.0069 | 2.6 | 0.0038 | |
| Error | 0.2583 | 98 | 0.0026 | |||
| Total | 0.5187 | 113 | ||||

3.3. Temperature Dependence of Release

3.4. Hydrogel Swelling and Its Effects

4. Conclusions
Appendix


| kkp Rate Constant | Factor B | |||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Preloaded | Postloaded | |||||||||||||
| Factor A | K+ | Temp = 25 | 0.163 | 0.308 | 0.151 | 0.163 | 0.130 | 0.079 | 0.169 | 0.231 | 0.294 | 0.167 | 0.287 | 0.114 |
| Temp = 31 | 0.385 | 0.077 | 0.134 | 0.148 | 0.084 | 0.084 | 0.182 | 0.096 | 0.144 | |||||
| Temp = 37 | 0.037 | 0.100 | 0.133 | 0.100 | 0.077 | 0.048 | 0.180 | 0.158 | 0.093 | 0.123 | 0.193 | 0.170 | ||
| Temp = 45 | 0.190 | 0.115 | 0.094 | 0.104 | 0.084 | 0.168 | 0.183 | 0.096 | 0.067 | |||||
| Ca2+ | Temp = 25 | 0.020 | 0.028 | 0.024 | 0.095 | 0.151 | 0.147 | 0.087 | 0.145 | 0.065 | 0.020 | 0.020 | 0.082 | |
| 0.082 | 0.088 | 0.076 | 0.098 | 0.025 | 0.096 | |||||||||
| Temp = 31 | 0.058 | 0.094 | 0.016 | 0.019 | 0.086 | 0.037 | 0.035 | 0.055 | 0.011 | 0.029 | 0.024 | 0.052 | ||
| 0.020 | 0.167 | 0.021 | 0.063 | 0.145 | 0.040 | |||||||||
| Temp = 37 | 0.105 | 0.065 | 0.065 | 0.050 | 0.032 | 0.087 | 0.135 | 0.076 | 0.173 | 0.020 | 0.022 | 0.035 | ||
| 0.040 | 0.087 | 0.160 | 0.118 | 0.113 | 0.069 | |||||||||
| Temp = 45 | 0.086 | 0.055 | 0.076 | 0.073 | 0.065 | 0.007 | 0.061 | 0.036 | 0.025 | 0.003 | 0.033 | 0.011 | ||
| 0.040 | 0.077 | 0.020 | 0.075 | 0.054 | 0.012 | |||||||||
| n Exponent | Factor B | |||||||||||||
| Preloaded | Postloaded | |||||||||||||
| Factor A | K+ | Temp = 25 | 0.33 | 0.19 | 0.35 | 0.33 | 0.38 | 0.49 | 0.29 | 0.25 | 0.19 | 0.44 | 0.19 | 0.44 |
| Temp = 31 | 0.11 | 0.55 | 0.39 | 0.28 | 0.42 | 0.43 | 0.27 | 0.41 | 0.30 | |||||
| Temp = 37 | 0.68 | 0.40 | 0.40 | 0.42 | 0.45 | 0.54 | 0.30 | 0.27 | 0.42 | 0.35 | 0.36 | 0.32 | ||
| Temp = 45 | 0.30 | 0.41 | 0.45 | 0.35 | 0.38 | 0.26 | 0.24 | 0.38 | 0.42 | |||||
| Ca2+ | Temp = 25 | 1.00 | 0.90 | 1.27 | 0.59 | 0.46 | 0.42 | 0.51 | 0.60 | 0.42 | 1.45 | 0.86 | 0.55 | |
| 0.53 | 0.48 | 0.67 | 0.46 | 0.81 | 0.61 | |||||||||
| Temp = 31 | 0.80 | 0.49 | 1.19 | 0.72 | 0.41 | 0.53 | 0.74 | 1.06 | 1.03 | 1.02 | 0.68 | 0.93 | ||
| 0.85 | 0.31 | 0.69 | 0.59 | 0.33 | 0.60 | |||||||||
| Temp = 37 | 0.44 | 0.62 | 0.58 | 0.63 | 0.93 | 0.63 | 0.66 | 0.59 | 0.38 | 1.02 | 1.12 | 1.64 | ||
| 0.65 | 0.50 | 0.33 | 0.39 | 0.43 | 0.46 | |||||||||
| Temp = 45 | 0.43 | 0.60 | 0.50 | 0.36 | 0.45 | 0.84 | 0.82 | 0.64 | 0.64 | 1.09 | 0.71 | 1.32 | ||
| 0.52 | 0.38 | 0.60 | 0.39 | 0.46 | 0.69 | |||||||||
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ottenbrite, R.M.; Park, K.; Okano, T. Biomedical Applications of Hydrogels Handbook, 1st ed.; Springer: New York, NY, USA, 2010; p. 700. [Google Scholar]
- Brahim, S.; Narinesingh, D.; Guiseppi-Elie, A. Synthesis and hydration properties of pH-sensitive, p(HEMA)-based hydrogels containing 3-(trimethoxysilyl)propyl methacrylate. Biomacromolecules 2003, 4, 497–503. [Google Scholar] [CrossRef] [PubMed]
- Porter, T.; Stewart, R.; Reed, J.; Morton, K. Models of hydrogel swelling with applications to hydration sensing. Sensors 2007, 7, 1980–1991. [Google Scholar] [CrossRef]
- Phelps, E.A.; Enemchukwu, N.O.; Fiore, V.F.; Sy, J.C.; Murthy, N.; Sulchek, T.A.; Barker, T.H.; García, A.J. Maleimide cross-linked bioactive PEG hydrogel exhibits improved reaction kinetics and cross-linking for cell encapsulation and in situ delivery. Adv. Mater. 2012, 24, 64–70. [Google Scholar] [CrossRef] [PubMed]
- Abraham, S.; Brahim, S.; Ishihara, K.; Guiseppi-Elie, A. Molecularly engineered p(HEMA)-based hydrogels for implant biochip biocompatibility. Biomaterials 2005, 26, 4767–4778. [Google Scholar] [CrossRef] [PubMed]
- Wichterie, O. Process for Producing Shaped Articles from Three-Dimensional. U.S. Patent 2976576 A, 28 May 1961. [Google Scholar]
- Yoon, H.Y.; Koo, H.; Choi, K.Y.; Lee, S.J.; Kim, K.; Kwon, I.C.; Leary, J.F.; Park, K.; Yuk, S.H.; Park, J.H. Tumor-targeting hyaluronic acid nanoparticles for photodynamic imaging and therapy. Biomaterials 2012, 33, 3980–3989. [Google Scholar] [CrossRef] [PubMed]
- Choi, N.W.; Kim, J.; Chapin, S.C.; Duong, T.; Donohue, E.; Pandey, P.; Broom, W.; Hill, W.A.; Doyle, P.S. Multiplexed detection of mRNA using porosity-tuned hydrogel microparticles. Anal. Chem. 2012, 84, 9370–9378. [Google Scholar] [PubMed]
- Bromberg, A.; Jensen, E.C.; Kim, J.; Jung, Y.K.; Mathies, R.A. Microfabricated linear hydrogel microarray for single-nucleotide polymorphism detection. Anal. Chem. 2011, 84, 963–970. [Google Scholar] [CrossRef] [PubMed]
- Wu, K.; Liu, J.; Johnson, R.N.; Yang, J.; Kopeček, J. Drug-Free macromolecular therapeutics: Induction of apoptosis by coiled-coil-mediated cross-linking of antigens on the cell surface. Angew. Chem. 2010, 122, 1493–1497. [Google Scholar] [CrossRef]
- Rustad, K.C.; Wong, V.W.; Sorkin, M.; Glotzbach, J.P.; Major, M.R.; Rajadas, J.; Longaker, M.T.; Gurtner, G.C. Enhancement of mesenchymal stem cell angiogenic capacity and stemness by a biomimetic hydrogel scaffold. Biomaterials 2012, 33, 80–90. [Google Scholar] [CrossRef] [PubMed]
- Guiseppi-Elie, A.; Brahim, S.; Narinesingh, D. A chemically synthesized artificial pancreas: Release of insulin from glucose-responsive hydrogels. Adv. Mater. 2002, 14, 743–746. [Google Scholar] [CrossRef]
- Kirschner, C.M.; Anseth, K.S. Hydrogels in healthcare: From static to dynamic material microenvironments. Acta Mater. 2013, 61, 931–944. [Google Scholar] [CrossRef] [PubMed]
- Hoffman, A.S. Stimuli-responsive polymers: Biomedical applications and challenges for clinical translation. Adv. Drug Deliv. Rev. 2013, 65, 10–16. [Google Scholar] [CrossRef] [PubMed]
- Wilson, A.N.; Guiseppi-Elie, A. Bioresponsive hydrogels. Adv. Healthc. Mater. 2013, 2, 520–532. [Google Scholar] [CrossRef] [PubMed]
- Wilson, A.N.; Guiseppi-Elie, A. Targeting homeostasis in drug delivery using bioresponsive hydrogel microforms. Int. J. Pharm. 2014, 461, 214–222. [Google Scholar] [CrossRef] [PubMed]
- Gordijo, C.R.; Koulajian, K.; Shuhendler, A.J.; Bonifacio, L.D.; Huang, H.Y.; Chiang, S.; Ozin, G.A.; Giacca, A.; Wu, X.Y. Nanotechnology-enabled closed loop insulin delivery device: In vitro and in vivo evaluation of glucose-regulated insulin release for diabetes control. Adv. Funct. Mater. 2011, 21, 73–82. [Google Scholar] [CrossRef]
- Kost, J.; Langer, R. Responsive polymeric delivery systems. Adv. Drug Deliv. Rev. 2012, 64, 327–341. [Google Scholar] [CrossRef]
- Qiu, Y.; Park, K. Environment-sensitive hydrogels for drug delivery. Adv. Drug Deliv. Rev. 2001, 53, 321–339. [Google Scholar] [CrossRef] [PubMed]
- Brandl, F.; Kastner, F.; Gschwind, R.M.; Blunk, T.; Teßmar, J.; Göpferich, A. Hydrogel-based drug delivery systems: Comparison of drug diffusivity and release kinetics. J. Control. Release 2010, 142, 221–228. [Google Scholar] [CrossRef] [PubMed]
- Wang, L.; Liu, M.; Gao, C.; Ma, L.; Cui, D. A pH-, thermo-, and glucose-, triple-responsive hydrogels: Synthesis and controlled drug delivery. React. Funct. Polym. 2010, 70, 159–167. [Google Scholar] [CrossRef]
- Korsmeyer, R.W.; Peppas, N.A. Effect of the morphology of hydrophilic polymeric matrices on the diffusion and release of water soluble drugs. J. Membr. Sci. 1981, 9, 211–227. [Google Scholar] [CrossRef]
- Ritger, P.L.; Peppas, N.A. A simple equation for description of solute release I. Fickian and non-Fickian release from non-swellable devices in the form of slabs, spheres, cylinders or discs. J. Control. Release 1987, 5, 23–36. [Google Scholar]
- Peppas, N.A.; Sahlin, J.J. A simple equation for the description of solute release. III. Coupling of diffusion and relaxation. Int. J. Pharm. 1989, 57, 169–172. [Google Scholar]
- Alfrey, T.; Gurnee, E.; Lloyd, W. Diffusion in glassy polymers. J. Polym. Sci. C Polym. Symp. 1966, 12, 249–261. [Google Scholar] [CrossRef]
- Hopfenberg, H.B.; Frisch, H.L. Transport of organic micromolecules in amorphous polymers. J. Polym. Sci. B 1969, 7, 405–409. [Google Scholar] [CrossRef]
- Aucoin, H.R.; Wilson, A.N.; Wilson, A.M.; Ishihara, K.; Guiseppi-Elie, A. Release of potassium ion and calcium ion from phosphorylcholine group bearing hydrogels. Polymers 2013, 5, 1241–1257. [Google Scholar] [CrossRef]
- Kotanen, C.N.; Wilson, A.N.; Wilson, A.M.; Ishihara, K.; Guiseppi-Elie, A. Biomimetic hydrogels gate transport of calcium ions across cell culture inserts. Biomed. Microdevices 2012, 14, 549–558. [Google Scholar] [CrossRef] [PubMed]
- Geise, G.M.; Freeman, B.D.; Paul, D.R. Sodium chloride diffusion in sulfonated polymers for membrane applications. J. Membr. Sci. 2013, 427, 186–196. [Google Scholar] [CrossRef]
- Watanabe, J.; Ishihara, K. Establishing ultimate biointerfaces covered with phosphorylcholine groups. Colloids Surf. B 2008, 65, 155–165. [Google Scholar] [CrossRef]
- Wallmersperger, T.; Ballhause, D.; Kröplin, B.; Günther, M.; Gerlach, G. Coupled multi-field formulation in space and time for the simulation of intelligent hydrogels. J. Intell. Mater. Syst. Struct. 2009, 20, 1483–1492. [Google Scholar] [CrossRef]
- Kang, B.; Dai, Y.-D.; Shen, X.-H.; Chen, D. Dynamical modeling and experimental evidence on the swelling/deswelling behaviors of pH sensitive hydrogels. Mater. Lett. 2008, 62, 3444–3446. [Google Scholar] [CrossRef]
- Guiseppi-Elie, A.; Dong, C.; Dinu, C.Z. Crosslink density of a biomimetic poly(HEMA)-based hydrogel influences growth and proliferation of attachment dependent RMS 13 cells. J. Mater. Chem. 2012, 22, 19529–19539. [Google Scholar] [CrossRef]
- Kotanen, C.N.; Wilson, A.N.; Dong, C.; Dinu, C.Z.; Justin, G.A.; Guiseppi-Elie, A. The effect of the physicochemical properties of bioactive electroconductive hydrogels on the growth and proliferation of attachment dependent cells. Biomaterials 2013, 34, 6318–6327. [Google Scholar] [CrossRef] [PubMed]
- Ishihara, K.; Ueda, T.; Nakabayashi, N. Preparation of phospholipid polymers and their properties as polymer hydrogel membranes. Polym. J. 1990, 22, 355–360. [Google Scholar] [CrossRef]
- Lang, W.; Zander, R. Physiological HEPES buffer proposed as a calibrator for pH measurement in human blood. Clin. Chem. Lab. Med. 1999, 37, 563–571. [Google Scholar] [CrossRef] [PubMed]
- Brannon-Peppas, L.; Peppas, N.A. Dynamic and equilibrium swelling behaviour of pH-sensitive hydrogels containing 2-hydroxyethyl methacrylate. Biomaterials 1990, 11, 635–644. [Google Scholar] [CrossRef] [PubMed]
- Flory, P.J.; Rehner, J., Jr. Statistical mechanics of cross-linked polymer networks I. Rubberlike elasticity. J. Chem. Phys. 1943, 11, 512–520. [Google Scholar]
- Huggins, M.L. Some properties of solutions of long-chain compounds. J. Phys. Chem. 1942, 46, 151–158. [Google Scholar] [CrossRef]
- Flory, P.J.; Rehner, J., Jr. Statistical mechanics of cross-linked polymer networks II. Swelling. J. Chem. Phys. 1943, 11, 521–526. [Google Scholar] [CrossRef]
- Brannon-Peppas, L.; Peppas, N.A. Equilibrium swelling behavior of pH-sensitive hydrogels. Chem. Eng. Sci. 1991, 46, 715–722. [Google Scholar] [CrossRef]
- Hooper, H.H.; Baker, J.P.; Blanch, H.W.; Prausnitz, J.M. Swelling equilibria for positively ionized polyacrylamide hydrogels. Macromolecules 1990, 23, 1096–1104. [Google Scholar] [CrossRef]
- Horkay, F.; Tasaki, I.; Basser, P.J. Effect of monovalent-divalent cation exchange on the swelling of polyacrylate hydrogels in physiological salt solutions. Biomacromolecules 2000, 2, 195–199. [Google Scholar] [CrossRef]
- Horkay, F.; Tasaki, I.; Basser, P.J. Osmotic swelling of polyacrylate hydrogels in physiological salt solutions. Biomacromolecules 2000, 1, 84–90. [Google Scholar] [CrossRef] [PubMed]
- Lee, W.F.; Lee, C.H. Poly(sulfobetaine)s and corresponding cationic polymers: 3. Synthesis and dilute aqueous solution properties of poly(sulfobetaine)s derived from styrene-maleic anhydride. Polymer 1997, 38, 971–979. [Google Scholar]
- Berlinova, I.V.; Dimitrov, I.V.; Kalinova, R.G.; Vladimirov, N.G. Synthesis and aqueous solution behaviour of copolymers containing sulfobetaine moieties in side chains. Polymer 2000, 41, 831–837. [Google Scholar] [CrossRef]
- Wang, T.; Wang, X.; Long, Y.; Liu, G.; Zhang, G. Ion-Specific conformational behavior of polyzwitterionic brushes: Exploiting it for protein adsorption/desorption control. Langmuir 2013, 29, 6588–6596. [Google Scholar] [CrossRef] [PubMed]
- Yoshihiro, K. Making phospholipid-type hydrogel for biomedical application with attention to crosslinking point. Ph.D. Thesis, Department of Materials Engineering, the University of Tokyo, Tokyo, Japan, 2004. [Google Scholar]
- Alencar de Queiroz, A.A.; Gallardo, A.; San Román, J. Vinylpyrrolidone-N,N'-dimethylacrylamide water-soluble copolymers: Synthesis, physical–chemical properties and proteic interactions. Biomaterials 2000, 21, 1631–1643. [Google Scholar] [CrossRef] [PubMed]
- Novikov, S. Charge-carrier transport in disordered polymers. J. Polym. Sci. B 2003, 41, 2584–2594. [Google Scholar] [CrossRef]
- Trongsatitkul, T.; Budhlall, B.M. Microgels or microcapsules? Role of morphology on the release kinetics of thermoresponsive PNIPAm-co-PEGMa hydrogels. Polym. Chem. 2013, 4, 1502–1516. [Google Scholar] [CrossRef]
© 2014 by the authors; licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution license (http://creativecommons.org/licenses/by/3.0/).
Share and Cite
Wilson, A.N.; Blenner, M.; Guiseppi-Elie, A. Polyplex Formation Influences Release Mechanism of Mono- and Di-Valent Ions from Phosphorylcholine Group Bearing Hydrogels. Polymers 2014, 6, 2451-2472. https://doi.org/10.3390/polym6092451
Wilson AN, Blenner M, Guiseppi-Elie A. Polyplex Formation Influences Release Mechanism of Mono- and Di-Valent Ions from Phosphorylcholine Group Bearing Hydrogels. Polymers. 2014; 6(9):2451-2472. https://doi.org/10.3390/polym6092451
Chicago/Turabian StyleWilson, A. Nolan, Mark Blenner, and Anthony Guiseppi-Elie. 2014. "Polyplex Formation Influences Release Mechanism of Mono- and Di-Valent Ions from Phosphorylcholine Group Bearing Hydrogels" Polymers 6, no. 9: 2451-2472. https://doi.org/10.3390/polym6092451
APA StyleWilson, A. N., Blenner, M., & Guiseppi-Elie, A. (2014). Polyplex Formation Influences Release Mechanism of Mono- and Di-Valent Ions from Phosphorylcholine Group Bearing Hydrogels. Polymers, 6(9), 2451-2472. https://doi.org/10.3390/polym6092451