One major goal of this study is to find out which measurements need to be conducted in order to achieve good prediction accuracy. In particular, the benefit of incorporating data from cyclic DSC measurements, which are necessary anyhow for characterization of the relationship between the glass transition temperature and the cure degree α, is demonstrated by firstly discussing results fitted without this data. Afterwards, the same is done under consideration of cyclic data in order to compare both cases.
For reasons of clarity and comprehensibility, the layout of the presentation of fitting results, consisting of three graphs placed side by side, is kept constant throughout the discussion. On the left graph, the predicted isothermal curing is plotted against time. The plot in the middle shows the model-prediction for non-isothermal temperature profiles and on the right, the consistence with cyclic DSC measurements is evaluated. The latter plot contains additional black lines which show the discrepancy between the prediction and the experimental data point.
5.2.1. Prediction Accuracy without Using Cyclic DSC Measurements
Figure 6 and
Figure 7 show the goodness of fit for both kinetic models in case only non-isothermal DSC data is used. As can be seen from the non-isothermal plots, the Grindling model is able to reproduce the experimental data very closely whereas the Kamal-Malkin model shows a significant deviation. From the plot on the right (
Figure 7c) it can be seen that the Grindling model shows good accuracy also for the isothermal conditions during cyclic DSC. However, the slope at the end of the curves on the isothermal plot (
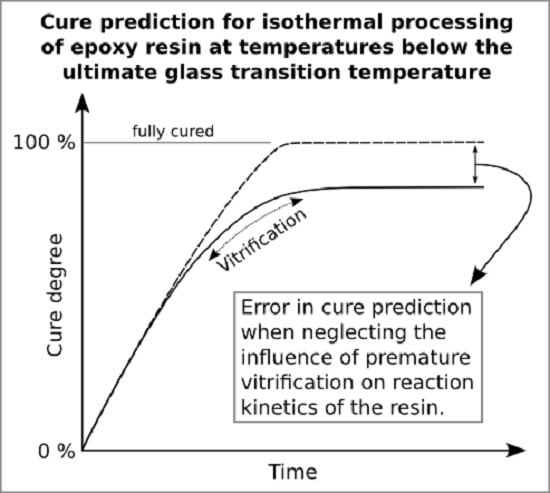
Figure 7a) is overestimated and does not exhibit slowing down of cross-linking due to vitrification (cf.
Figure 2).
In
Section 4 it was concluded that fitting to only isothermal data is not advisable.
Figure 8 and
Figure 9 show the result of the fitting algorithm for this situation for Kamal-Malkin and Grindling kinetic model, respectively. Obviously, prediction accuracy of both models is poor which is especially evident from the comparison with cyclic DSC data. The algorithm overpredicts the initial cure degree such that all isothermal curves eventually end up at full cure
. As a consequence, the reaction never has to take place under diffusion-controlled conditions. This leads to very similar cure predictions since the Grindling model is an extension of the Kamal-Malkin model and behaves similar in the absence of vitrification (cf.
Section 3.2). Therefore, as has been mentioned before, using only isothermal data for kinetic model fitting is not sufficient.
By using non-isothermal as well as isothermal data as the fitting target, it is possible to iteratively calculate the initial cure degree for the experimental isothermal curves. When comparing the corresponding plots in
Figure 10 and
Figure 11, the advantage of diffusion-controlled kinetics in case of the Grindling kinetic model becomes obvious. The Kamal-Malkin model is not able to reproduce both isothermal and non-isothermal data in a sufficient way. From
Figure 10a it is visible that the fitting algorithm chooses the initial cure degrees such that all curves reach a cure level of 100%. This was to be expected since the model is not capable of modeling vitrification effects. This model actually delivered much better prediction accuracy for non-isothermal and isothermal processing when only non-isothermal data was used for fitting (cf.
Figure 6). The Grindling model shows very good prediction accuracy for both temperature programs due to its ability to adjust the cure rate not only to cure temperature but also to the current glass transition temperature.
5.2.2. Prediction Accuracy Using Cyclic DSC Measurements
Up to this point, kinetic model fitting was carried out without using data from cyclic DSC measurements. However, when using diffusion-controlled kinetic models, these measurements need to be performed anyway in order to characterize the dependency of on cross-linking. It may therefore be beneficial to also use them for fitting of kinetic models.
By comparing
Figure 6 and
Figure 12, it becomes evident that by adding cyclic data to the fitting target, the prediction accuracy of the Kamal-Malkin kinetic model for isothermal processing is improved considerably. This is especially evident when comparing the match with cyclic DSC measurements (cf.
Figure 6c and
Figure 12c). However, the slope at the end of isothermal curves still remains too steep. The reason for that is the type of data which is gathered from cyclic DSC runs. In contrast to pure isothermal measurements, cyclic DSC measurements as they are evaluated in the present paper, only provide data at distinct points. More specifically, there is no information about how a specific cure degree was reached or for how long a possible vitrification might have been present. As can be seen in
Figure 7 and
Figure 13, the Grindling model shows slightly better accuracy after adding cyclic data to the fitting target. Moreover, a sudden transition from chemically-controlled to diffusion-controlled reaction is indicated by a kink in the curve for isothermal cure at 60
C in
Figure 13a.
In general, it is observed that isothermal cure prediction gains in accuracy by adding cyclic data to the fitting target, which apart from that only consists of non-isothermal data. At the same time, prediction quality for non-isothermal conditions decreases when applying the Grindling model (cf.
Figure 7b and
Figure 13b). This was to be expected since the model now has to not only reproduce non-isothermal curing, but also, at least to some extent, isothermal processing in the form of cyclic DSC. The opposite is observed in case of the Kamal-Malkin model, which shows a slight improvement in non-isothermal cure predictions, particularly for low heat rates (cf.
Figure 6b and
Figure 12b).
When fitting to solely isothermal data, the match between experimental and numerical curves improves significantly by additionally incorporating cyclic data into the fitting target. This is visible in
Figure 8 and
Figure 14 for the Kamal-Malkin kinetic model and in
Figure 9 and
Figure 15 for the Grindling kinetic model. However, the gain is more pronounced in case of the latter model.
The Kamal-Malkin model compensates for premature vitrification under isothermal conditions by significantly slowing down the reaction after reaching medium high cure levels (cf.
Figure 14a). The match with cyclic DSC data is therefore good but even though the reaction is slowed down, it will reach full cure for longer periods of time. Moreover, vitrification occurs for distinct isothermal temperatures at different cure levels which the Kamal-Malkin kinetic model is not able to account for. This results in a too early slow down of the reaction in case of the lowest as well as a too late slow down for the highest isothermal temperature. Hence, the glass transition temperature which is directly related to the cure degree is underestimated, or in the latter case, overrated. This can have a significant impact when using such predictions for process simulation since many material properties depend on the glass transition temperature and whether the material is in glassy or rubbery state.
Although none of the non-isothermal experimental data is used for fitting both models give good predictions for non-isothermal curing. The accuracy is best for the lowest heating rate which is due to the fact that the isothermal measurements provide many data points for widespread values of cure degree within a temperature range of 60 to 120
C. Most of the reaction of specimens which are cured at a heating rate of 1
C/min, happens within this temperature range (cf.
Figure 14c and
Figure 15c) and therefore the model is able to accurately predict the curing process. The agreement between model prediction and experiment declines as the heating rate is increased because the reaction is shifted towards higher temperatures which require the kinetic models to extrapolate the temperature dependency of the cure rate into this region. This introduces deviations which are most evident in case of the highest heating rate of 15
C/min (cf.
Figure 14b and
Figure 15b).
Figure 10 and
Figure 16 show the difference between fitting to non-isothermal as well as isothermal and doing so with additionally using cyclic data in case of the Kamal-Malkin kinetic model. An improvement is visible for each measurement type. However, isothermal cure predictions still end up at too high values of cure degree, which again arises from the fact, that the model is not able to render vitrification effects. The slow down in cure rate, which was observed when fitting against isothermal and cyclic data (cf.
Figure 14a), is less pronounced in this case. This is due to a change in weighting of each of the measurement types. If fitting is carried out under consideration of only isothermal and cyclic data, vitrification is present in all of the experimental data. However, this is not the case for non-isothermal data and by adding this type of measurement to the fitting process, data with vitrification loses in weight.
On the contrary, by comparing the results of the Grindling model in
Figure 11 and
Figure 17, a very good match between experiment and model is observed regardless of whether cyclic data is used for fitting or not. The slight deviations may also arise from the fitting algorithm itself. However, by comparing
Figure 15b and
Figure 17b, it is observed that by adding non-isothermal data to the fitting target, the prediction accuracy for this type of processing is improved whereas at the same time, the match with cyclic data loses in quality. This is again because of the fact that the model now has to satisfy a more comprehensive situation.
In order to simplify the comparison of the different fitting results, the goodness of fit is quantified by standard errors, as summarized in
Table 2. In this table, non-isothermal and isothermal DSC measurements are abbreviated as dyn and iso, respectively. Lower values of standard error denote a better accordance between measurement and model prediction. However, it is important to mention that the prediction quality for isothermal conditions is overrated when the initially lost amount of cross-linking is overestimated by the fitting algorithm. This is observed for both models when fitted against solely isothermal data, and in case of the Kamal-Malkin model when fitted to isothermal and non-isothermal data. On the contrary, the prediction accuracy for isothermal curing is underrated when isothermal measurements are not used for model fitting, since the initial cure degrees cannot be estimated under this circumstances. In this case, the standard error is calculated with the assumption of zero initial cure (cf.
Figure 2a). Corresponding values of standard error are marked accordingly in
Table 2. Due to the mentioned restrictions, the validity and comparability of the shown standard errors is limited. Interpretation of the data in
Table 2 should therefore always be accompanied by visual comparison of corresponding cure predictions.
Since it is favorable to reduce the needed amount of measurements,
Figure 18 shows the fitting quality of the Grindling kinetic model in case cyclic data and only a reduced set of isothermal and non-isothermal measurements are used for model parametrization. The isothermal data is limited to the temperatures 60, 80 and 100
C. In case of non-isothermal DSC, only results for heating rates of 1, 5 and 15
C/min are used.
By comparing
Figure 17a and
Figure 18a only minor differences can be identified. This suggests that isothermal measurements at high temperatures close to the ultimate glass transition temperature
can be omitted. This may be due to the fact that at this elevated temperatures, the influence of vitrification is much smaller compared to lower temperatures. Since DSC data of isothermal curing at 120
C was not used for fitting, a corresponding initial degree of cure was not predicted. Therefore, the experimental curve in
Figure 18a shows far too low cure degrees.
Prediction quality for non-isothermal processing (cf.
Figure 17b and
Figure 18b) loses in accuracy. However, this is acceptable since for the majority of composite manufacturing processes, i.e., RTM, good and accurate results for isothermal temperature programs is much more important. Furthermore, the match with cyclic data is improved (cf.
Figure 17c and
Figure 18c) which again is advantageous for modeling of isothermal processes.
It should be clear from the above that the often applied approach of only using non-isothermal DSC measurements for kinetic model parametrization is not suitable for prediction of isothermal curing at temperatures below the ultimate glass transition temperature. Instead, the results of the present study indicate that the non-isothermal measurements are actually not as important as the isothermal ones. This is due to the fact that isothermal measurements contain information of both, cross-linking with and without influence of vitrification. Non-isothermal DSC shows this effect only for very low heating rates, for which the glass transition temperature is able to catch up with the reaction temperature. This results in a temporarily decrease in reaction rate. However, since the temperature is continuously increased, non-isothermal DSC data does not contain information about a complete stop in reaction as is observed under isothermal conditions. Using isothermal measurements for model parametrization, however, requires the fitting strategy to account for the initially lost amount of cure which cannot be avoided when conducting DSC measurements of fast resins at elevated isothermal temperatures. By iteratively approximating the initial cure degrees during fitting, as presented in this study, this major drawback of isothermal DSC runs was successfully eliminated.