Correlation-Based Multiplexing of Complex Amplitude Data Pages in a Holographic Storage System Using Digital Holographic Techniques
Abstract
:1. Introduction
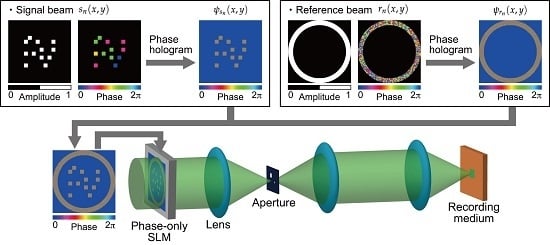
2. Correlation-Based Multiplexing in a Holographic Storage System with Digital Holographic Techniques
3. Experimental Demonstration
3.1. Single Recording
3.2. Correlation-Based Multiplexing
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Hesselink, L.; Orlov, S.S.; Bashaw, M.C. Holographic data storage systems. Proc. IEEE 2004, 92, 1231–1280. [Google Scholar] [CrossRef]
- Dhar, L.; Curtis, K.; Fäcke, T. Holographic data storage: Coming of age. Nat. Photon. 2008, 2, 403–405. [Google Scholar] [CrossRef]
- Curtis, K.; Dhar, L.; Hill, A.; Wilson, W.; Ayres, M. Holographic Data Storage: From Theory to Practical Systems; John Wiley & Sons: Chichester, UK, 2010. [Google Scholar]
- Mitsube, K.; Nishimura, Y.; Nagaya, K.; Takayama, S.; Tomita, Y. Holographic nanoparticle-polymer composites based on radical-mediated thiol-yne photopolymerizations: Characterization and shift-multiplexed holographic digital data page storage. Opt. Mater. Express 2014, 4, 982–996. [Google Scholar] [CrossRef]
- Li, C.; Cao, L.; Wang, Z.; Jin, G. Hybrid polarization-angle multiplexing for volume holography in gold nanoparticle-doped photopolymer. Opt. Lett. 2014, 39, 6891–6894. [Google Scholar] [CrossRef] [PubMed]
- Navarro-Fuster, V.; Ortuño, M.; Fernández, R.; Gallego, S.; Márquez, A.; Beléndez, A.; Pascual, I. Peristrophic multiplexed holograms recorded in a low toxicity photopolymer. Opt. Mater. Express 2017, 7, 133–147. [Google Scholar] [CrossRef]
- Isogai, R.; Nakamura, Y.; Takagi, H.; Goto, T.; Lim, P.B.; Inoue, M. Thermomagnetic writing into magnetophotonic microcavities controlling thermal diffusion for volumetric magnetic holography. Opt. Express 2016, 24, 522–527. [Google Scholar] [CrossRef] [PubMed]
- Horimai, H.; Tan, X.; Liu, J. Collinear holography. Appl. Opt. 2005, 44, 2575–2579. [Google Scholar] [CrossRef] [PubMed]
- Hoskins, A.; Ihas, B.; Anderson, K.; Curtis, K. Monocular architecture. Jpn. J. Appl. Phys. 2008, 47, 5912–5914. [Google Scholar] [CrossRef]
- Hoskins, A.; Ihas, B.; Anderson, K.; Curtis, K. New optical architecture for holographic data storage system compatible with Blu-ray DiscTM system. Opt. Eng. 2014, 53, 025102. [Google Scholar]
- Takabayashi, M.; Okamoto, A. Self-referential holography and its applications to data storage and phase-to-intensity conversion. Opt. Express 2013, 21, 3669–3681. [Google Scholar] [CrossRef] [PubMed]
- Betin, A.Y.; Bobrinev, V.I.; Odinokov, S.B.; Evtikhiev, N.N.; Starikov, R.S.; Starikov, S.N.; Zlolazov, E.Y. Holographic memory optical system based on computer-generated Fourier holograms. Appl. Opt. 2013, 52, 8142–8145. [Google Scholar] [CrossRef] [PubMed]
- Yosida, S.; Kurata, H.; Ozawa, S.; Okubo, K.; Horiuchi, S.; Ushiyama, Z.; Yamamoto, M.; Koga, S.; Tanaka, A. High-density holographic data storage using three-dimensional shift multiplexing with spherical reference wave. Jpn. J. Appl. Phys. 2013, 52, 09LD07. [Google Scholar] [CrossRef]
- Nobukawa, T.; Nomura, T. Multilayer recording holographic data storage using a varifocal lens generated with a kinoform. Opt. Lett. 2015, 40, 5419–5422. [Google Scholar] [CrossRef] [PubMed]
- Nobukawa, T.; Nomura, T. Digital super-resolution holographic data storage based on Hermitian symmetry for achieving high areal density. Opt. Express 2017, 25, 1326–1338. [Google Scholar] [CrossRef] [PubMed]
- Zang, J.; Kang, G.; Li, P.; Liu, Y.; Fan, F.; Hong, Y.; Huang, Y.; Tan, X.; Wu, A.; Shimura, T.; et al. Dual-channel recording based on the null reconstruction effect of orthogonal linear polarization holography. Opt. Lett. 2017, 42, 1377–1380. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.W.; Xiao, S.; Cheng, C.Y.; Sun, C.C. One-shot and aberration-tolerable homodyne detection for holographic storage readout through double-frequency grating-based lateral shearing interferometry. Opt. Express 2016, 24, 10412–10423. [Google Scholar] [CrossRef] [PubMed]
- Miller, B.E.; Takashima, Y. Cavity techniques for holographic data storage recording. Opt. Express 2016, 24, 6300–6317. [Google Scholar] [CrossRef] [PubMed]
- Muroi, T.; Katano, Y.; Kinoshita, N.; Ishii, N. Dual-page reproduction to increase the data transfer rate in holographic memory. Opt. Lett. 2013, 42, 2287–2290. [Google Scholar] [CrossRef] [PubMed]
- Hosaka, M.; Ishii, T.; Tanaka, A.; Koga, S.; Hoshizawa, T. 1 Tbit/inch2 recording in angular-multiplexing holographic memory with constant signal-to-scatter ratio schedule. Jpn. J. Appl. Phys. 2013, 52, 09LD01. [Google Scholar] [CrossRef]
- Ayres, M.; Anderson, K.; Askham, F.; Sissom, B.; Urness, A.C. Multi-terabit/in2 holographic data storage demonstration. Proc. SPIE 2015, 9587, 958702. [Google Scholar]
- Berger, G.; Dietz, M.; Denz, C. Hybrid multinary modulation codes for page-oriented holographic data storage. J. Opt. A Pure Appl. Opt. 2008, 10, 115305. [Google Scholar] [CrossRef]
- Das, B.; Joseph, J.; Singh, K. Phase-image-based sparse-gray-level data pages for holographic data storage. Appl. Opt. 2009, 48, 5240–5250. [Google Scholar] [CrossRef] [PubMed]
- Bunsen, M.; Umetsu, S.; Takabayashi, M.; Okamoto, A. Method of phase and amplitude modulation/demodulation using datapages with embedded phase-shift for holographic data storage. Jpn. J. Appl. Phys. 2013, 52, 09LD04. [Google Scholar] [CrossRef]
- Nobukawa, T.; Nomura, T. Multilevel recording of complex amplitude data pages in a holographic data storage system using digital holography. Opt. Express 2016, 18, 21001–21011. [Google Scholar] [CrossRef] [PubMed]
- Yu, Y.W.; Teng, T.C.; Hsieh, S.C.; Cheng, C.Y.; Sun, C.C. Shifting selectivity of collinear volume holographic storage. Opt. Commun. 2010, 283, 3895–3900. [Google Scholar] [CrossRef]
- Sun, C.C.; Su, W.C. Three-dimensional shifting selectivity of random phase encoding in volume holograms. Appt. Opt. 2001, 40, 1253–1260. [Google Scholar] [CrossRef]
- Shibukawa, A.; Okamoto, A.; Tomita, A.; Takabayashi, M.; Sato, K. Multilayer collinear holographic memory with movable random phase mask. Jpn. J. Appl. Phys. 2011, 50, 09ME10. [Google Scholar] [CrossRef]
- Cao, L.; Liu, J.; He, Q.; Jin, G. Orthogonal reference pattern multiplexing for collinear holographic data storage. Appl. Opt. 2014, 53, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Nobukawa, T.; Nomura, T. Design of high-resolution and multilevel reference pattern for improvement of both light utilization efficiency and signal-to-noise ratio in coaxial holographic data storage. Appl. Opt. 2014, 53, 3773–3781. [Google Scholar] [CrossRef] [PubMed]
- Nobukawa, T.; Wani, Y.; Nomura, T. Multiplexed recording with uncorrelated computer-generated reference patterns in coaxial holographic data storage. Opt. Lett. 2015, 40, 2161–2164. [Google Scholar] [CrossRef] [PubMed]
- Shimura, T.; Ichimura, S.; Fujimura, R.; Kuroda, K.; Tan, X.; Horimai, H. Analysis of a collinear holographic storage system: Introduction of pixel spread function. Opt. Lett. 2006, 31, 1208–1210. [Google Scholar] [CrossRef] [PubMed]
- Tanaka, K.; Hara, M.; Tokuyama, K.; Hirooka, K.; Ishioka, K.; Fukumoto, A.; Watanabe, K. Improved performance in coaxial holographic data recording. Opt. Express 2007, 15, 16196–16209. [Google Scholar] [CrossRef] [PubMed]
- Ni, K.; Ren, W.; Qu, Z.; Cao, L.; He, Q.; Jin, G. Phase-modulated multigroup volume holographic correlator. Opt. Lett. 2008, 33, 1144–1146. [Google Scholar] [CrossRef] [PubMed]
- Ikeda, K.; Suzuki, H.; Watanabe, E. Optical correlation-based cross-domain image retrieval system. Opt. Lett. 2017, 42, 2603–2606. [Google Scholar] [CrossRef]
- Davis, J.A.; Cottrell, D.M.; Campos, J.; Yzuel, M.J.; Moreno, I. Encoding amplitude information onto phase-only filters. Appl. Opt. 1999, 38, 5004–5013. [Google Scholar] [CrossRef] [PubMed]
- Arrizón, V.; Ruiz, U.; Carrada, R.; González, L.A. Pixelated phase computer holograms for the accurate encoding of scalar complex fields. J. Opt. Soc. Am. A 2007, 38, 3500–3507. [Google Scholar] [CrossRef]
- Arrizón, V.; Ruiz, U.; Carrada, R.; González, L.A. Exact solution to simultaneous intensity and phase encryption with a single phase-only hologram. Opt. Lett. 2013, 38, 3546–3549. [Google Scholar]
- Nobukawa, T.; Nomura, T. Linear phase encoding for holographic data storage with a single phase-only spatial light modulator. Appl. Opt. 2016, 55, 2565–2573. [Google Scholar] [CrossRef] [PubMed]
- Burr, G.W.; Barking, G.; Coufal, H.; Hoffnagle, J.A.; Jefferson, C.M.; Neifeld, M.A. Gray-scale data pages for digital holographic data storage. Opt. Lett. 1998, 23, 1218–1220. [Google Scholar] [CrossRef] [PubMed]
- Takeda, M.; Ina, H.; Kobayashi, S. Fourier-transform method of fringe-pattern analysis for computer-based topography and interferometry. J. Opt. Soc. Am. 1982, 72, 156–160. [Google Scholar] [CrossRef]
- King, B.M.; Neifeld, M.A. Sparse modulation coding for increased capacity in volume holographic storage. Appl. Opt. 2000, 39, 6681–6688. [Google Scholar] [CrossRef] [PubMed]
- Hong, J.; McMichael, I.; Ma, J. Influence of phase masks on cross talk in holographic memory. Opt. Lett. 1996, 21, 1694–1696. [Google Scholar] [CrossRef] [PubMed]
- Bernal, M.-P.; Burr, G.W.; Coufal, H.; Quintanilla, M. Balancing interpixel cross talk and detector noise to optimize areal density in holographic storage systems. Appl. Opt. 1998, 37, 5377–5385. [Google Scholar] [CrossRef] [PubMed]












© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nobukawa, T.; Nomura, T. Correlation-Based Multiplexing of Complex Amplitude Data Pages in a Holographic Storage System Using Digital Holographic Techniques. Polymers 2017, 9, 375. https://doi.org/10.3390/polym9080375
Nobukawa T, Nomura T. Correlation-Based Multiplexing of Complex Amplitude Data Pages in a Holographic Storage System Using Digital Holographic Techniques. Polymers. 2017; 9(8):375. https://doi.org/10.3390/polym9080375
Chicago/Turabian StyleNobukawa, Teruyoshi, and Takanori Nomura. 2017. "Correlation-Based Multiplexing of Complex Amplitude Data Pages in a Holographic Storage System Using Digital Holographic Techniques" Polymers 9, no. 8: 375. https://doi.org/10.3390/polym9080375
APA StyleNobukawa, T., & Nomura, T. (2017). Correlation-Based Multiplexing of Complex Amplitude Data Pages in a Holographic Storage System Using Digital Holographic Techniques. Polymers, 9(8), 375. https://doi.org/10.3390/polym9080375