Light-Driven Liquid Crystal Circular Dammann Grating Fabricated by a Micro-Patterned Liquid Crystal Polymer Phase Mask
Abstract
:1. Introduction
2. Materials and Methods
2.1. Fundamentals of Circular Dammann Grating
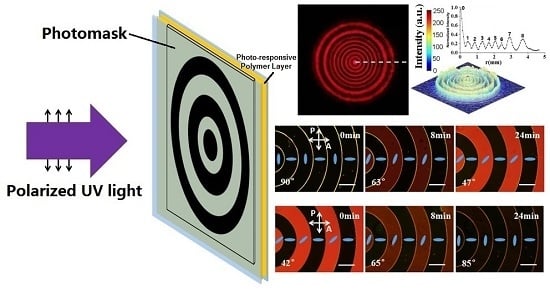
2.2. Method of Fabricating Liquid Crystal Circular Dammann Gratings
2.3. Characterization
2.4. Method of Optically Tuning a Liquid Crystal Circular Dammann Grating
3. Results and Discussion
3.1. Efficiencies and Uniformities of Liquid Crystal Circular Dammann Gratings
3.2. Microstructures and Far-Field Light Intensity Distributions
3.3. Optical Tunability of a Liquid Crystal Circular Dammann Grating
3.4. Electrical Tunability of a Liquid Crystal Circular Dammann Grating
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Zhu, G.; Li, J.N.; Lin, X.W.; Wang, H.F.; Hu, W.; Zheng, Z.G.; Cui, H.Q.; Shen, D.; Lu, Y.Q. Polarization-independent blue-phase liquid-crystal gratings driven by vertical electric field. J. Soc. Inf. Disp. 2012, 20, 341–346. [Google Scholar] [CrossRef]
- Wang, X.Q.; Yang, W.Q.; Liu, Z.; Duan, W.; Hu, W.; Zheng, Z.G.; Shen, D.; Chigrinov, V.G.; Kwok, H.S. Switchable Fresnel lens based on hybrid photo-aligned dual frequency nematic liquid crystal. Opt. Mater. Express 2017, 7, 8–15. [Google Scholar] [CrossRef]
- Tam, A.M.W.; Fan, F.; Du, T.; Hu, W.; Zhang, W.L.; Zhao, C.X.; Wang, X.Q.; Ching, K.L.; Li, G.J.; Luo, H.L.; et al. Bifocal optical-vortex lens with sorting of the generated nonseparable spin-orbital angular-momentum states. Phys. Rev. Appl. 2017, 7, 034010. [Google Scholar] [CrossRef]
- Wei, B.Y.; Chen, P.; Hu, W.; Ji, W.; Zheng, L.Y.; Ge, S.J.; Ming, Y.; Chigrinov, V.; Lu, Y.Q. Polarization-controllable Airy beams generated via a photoaligned director-variant liquid crystal mask. Sci. Rep. 2015, 5, 17484. [Google Scholar] [CrossRef] [PubMed]
- Fan, F.; Yao, L.S.; Wang, X.Q.; Shi, L.Y.; Srivastava, A.K.; Chigrinov, V.G.; Kwok, H.S.; Wen, S.C. Ferroelectric Liquid Crystal Dammann Grating by Patterned Photoalignment. Crystals 2017, 7, 79. [Google Scholar] [CrossRef]
- Lee, C.R.; Lo, K.C.; Mo, T.S. Electrically switchable fresnel lens based on a liquid crystal film with a polymer relief pattern. Jpn. J. Appl. Phys. 2007, 46, 4144–4147. [Google Scholar] [CrossRef]
- Lou, Y.M.; Liu, Q.K.; Wang, H.; Shi, Y.C.; He, S.L. Rapid fabrication of an electrically switchable liquid crystal Fresnel zone lens. Appl. Opt. 2010, 49, 4995–5000. [Google Scholar] [CrossRef] [PubMed]
- Lu, J.G.; Sun, X.F.; Song, Y.; Shieh, H.P.D. 2-D/3-D Switchable Display by Fresnel-Type LC Lens. J. Disp. Technol. 2011, 7, 215–219. [Google Scholar] [CrossRef]
- Lin, C.H.; Huang, H.Y.; Wang, J.Y. Polarization-independent liquid-crystal Fresnel lenses based on surface-mode switching of 90° twisted-nematic liquid crystals. IEEE Photonics Technol. Lett. 2010, 22, 137–139. [Google Scholar] [CrossRef]
- Wang, F.; Shao, L.S.; Bai, Q.Y.; Che, X.Y.; Liu, B.; Wang, Y.H. Photo-induced vertical alignment of liquid crystals via In situ polymerization initiated by polyimide containing benzophenone. Polymers 2017, 9, 9060233. [Google Scholar] [CrossRef]
- Wang, X.Q.; Fan, F.; Du, T.; Tam, A.M.W.; Ma, Y.; Srivastava, A.K.; Chigrinov, V.G.; Kwok, H.S. Liquid crystal Fresnel zone lens based on single-side-patterned photoalignment layer. Appl. Opt. 2014, 53, 2026–2029. [Google Scholar] [CrossRef] [PubMed]
- Wang, X.Q.; Srivastava, A.K.; Chigrinov, V.G.; Kwok, H.S. Switchable Fresnel lens based on micropatterned alignment. Opt. Lett. 2013, 38, 1775–1777. [Google Scholar] [CrossRef] [PubMed]
- Srivastava, A.K.; Wang, X.Q.; Gong, S.Q.; Shen, D.; Lu, Y.Q.; Chigrinov, V.G.; Kwok, H.S. Micro-patterned photo-aligned ferroelectric liquid crystal Fresnel zone lens. Opt. Lett. 2015, 40, 1643–1646. [Google Scholar] [CrossRef] [PubMed]
- Chigrinov, V.G.; Srivastava, A. Ferroelectric liquid crystal cells for advanced applications in displays and photonics. Mol. Cryst. Liq. Cryst. 2014, 595, 39–49. [Google Scholar] [CrossRef]
- Ge, S.J.; Chen, P.; Ma, L.L.; Liu, Z. Optical array generator based on blue phase liquid crystal Dammann grating. Opt. Mater. Express 2016, 6, 1087–1092. [Google Scholar] [CrossRef]
- Wang, X.Q.; Srivastava, A.K.; Fan, F.; Zheng, Z.G.; Shen, D.; Chigrinov, V.G.; Kwok, H.S. Electrically/optically tunable photo-aligned hybrid nematic liquid crystal Dammann grating. Opt. Lett. 2016, 41, 5668–5671. [Google Scholar] [CrossRef] [PubMed]
- Luo, D.; Sun, X.W.; Dai, H.T.; Demir, V.H. Polarization-dependent circular Dammann grating made of azo-dye-doped liquid crystals. Appl. Opt. 2011, 50, 2316–2321. [Google Scholar] [CrossRef] [PubMed]
- Song, Q.; Xianyu, H.Q.; Gauza, S.; Wu, S.T. High Birefringence and Low Crossover Frequency Dual-Frequency Liquid Crystals. Mol. Cryst. Liq. Cryst. 2008, 488, 179–189. [Google Scholar] [CrossRef]
- Xianyu, H.Q.; Wu, S.T.; Lin, C.L. Dual frequency liquid crystals: A review. Liq. Cryst. 2009, 36, 717–726. [Google Scholar] [CrossRef]
- Yukitaka, S.; Liu, J.P.; Chung, P.S.; Dobson, K.; Zhou, X.; Poon, T.C. Three-dimensional complex image coding using a circular Dammann grating. Appl. Opt. 2011, 50, 38–45. [Google Scholar] [CrossRef]
- Zhao, S.; Chung, P.S. Collimation testing using a circular Dammann grating. Opt. Commun. 2007, 279, 1–6. [Google Scholar] [CrossRef]
- Wen, F.J.; Chung, P.S. Use of the circular Dammann grating in angle measurement. Appl. Opt. 2008, 47, 5197–5200. [Google Scholar] [CrossRef] [PubMed]
- Wen, F.J.; Chen, Z.Y.; Chung, P.S. Area measurement at long-distance using a circular Dammann grating. Appl. Opt. 2010, 49, 648–652. [Google Scholar] [CrossRef] [PubMed]
- Zhou, C.H.; Jia, J.; Liu, L.R. Circular Dammann grating. Opt. Lett. 2003, 28, 2174–2176. [Google Scholar] [CrossRef] [PubMed]
- Zhao, S.; Chung, P.S. Design of a circular Dammann grating. Opt. Lett. 2006, 31, 2387–2389. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.C.; Gao, N.; Xie, C.Q. Using circular Dammann gratings to produce impulse optic vortex rings. Appl. Phys. Lett. 2012, 100, 041107–041110. [Google Scholar] [CrossRef]
- Lei, T.; Zhang, M.; Li, Y.R.; Jia, P.; Liu, G.N.; Xu, X.G.; Li, Z.H.; Min, C.J.; Lin, J.; Yu, C.Y.; Niu, H.B.; Yuan, X.C. Massive individual orbital angular momentum channels for multiplexing enabled by Dammann gratings. Light Sci. Appl. 2015, 4, e257. [Google Scholar] [CrossRef]
- Hu, W.; Srivastava, A.K.; Lin, X.W.; Liang, X.; Wu, Z.J. Polarization independent liquid crystal gratings based on orthogonal photoalignments. Appl. Phys. Lett. 2012, 100, 111116. [Google Scholar] [CrossRef]
- Akiyama, H.; Kawara, T.; Takada, H.; Takatsu, H.; Chigrinov, V.; Prudnikova, E.; Kozenkov, V.; Kwok, H. Synthesis and properties of azo dye aligning layers for liquid crystal cells. Liq. Cryst. 2002, 29, 1321–1327. [Google Scholar] [CrossRef]
- Chigrinov, V.; Pikin, S.; Verevochnikov, A.; Kozenkov, V.; Khazimullin, M.; Ho, J.; Huang, D.D.; Kwok, H.S. Diffusion model of photoaligning in azo-dye layers. Phys. Rev. E 2004, 69, 061713. [Google Scholar] [CrossRef] [PubMed]
- Muravsky, A.; Murauski, A.; Li, X.H.; Chigrinov, V.; Kwok, H.S. Optical rewritable liquid-crystal-alignment technology. J. Soc. Inf. Disp. 2007, 15, 267–273. [Google Scholar] [CrossRef]
- Sun, J.; Srivastava, A.K.; Wang, L.; Chigrinov, V.G.; Kwok, H.S. Optically tunable and rewritable diffraction grating with photoaligned liquid crystals. Opt. Lett. 2013, 38, 2342–2344. [Google Scholar] [CrossRef] [PubMed]



| Order Number | Normalized Radius ai | Efficiency | Uniformity |
|---|---|---|---|
| 3 | 0.2178, 0.3922, 0.7194 | 78.6% | 0.0765 |
| 8 | 0.0962, 0.1936, 0.2894, 0.3904, 0.4854, 0.5966, 0.6844, 0.8856 | 76.4% | 0.0420 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Wu, S.; Yang, W.; Yuan, C.; Li, X.; Liu, Z.; Tseng, M.; Chigrinov, V.G.; Kwok, H.; Shen, D.; et al. Light-Driven Liquid Crystal Circular Dammann Grating Fabricated by a Micro-Patterned Liquid Crystal Polymer Phase Mask. Polymers 2017, 9, 380. https://doi.org/10.3390/polym9080380
Wang X, Wu S, Yang W, Yuan C, Li X, Liu Z, Tseng M, Chigrinov VG, Kwok H, Shen D, et al. Light-Driven Liquid Crystal Circular Dammann Grating Fabricated by a Micro-Patterned Liquid Crystal Polymer Phase Mask. Polymers. 2017; 9(8):380. https://doi.org/10.3390/polym9080380
Chicago/Turabian StyleWang, Xiaoqian, Saibo Wu, Weiqiang Yang, Conglong Yuan, Xiao Li, Zhen Liu, Manchun Tseng, Vladimir G. Chigrinov, Hoising Kwok, Dong Shen, and et al. 2017. "Light-Driven Liquid Crystal Circular Dammann Grating Fabricated by a Micro-Patterned Liquid Crystal Polymer Phase Mask" Polymers 9, no. 8: 380. https://doi.org/10.3390/polym9080380
APA StyleWang, X., Wu, S., Yang, W., Yuan, C., Li, X., Liu, Z., Tseng, M., Chigrinov, V. G., Kwok, H., Shen, D., & Zheng, Z. (2017). Light-Driven Liquid Crystal Circular Dammann Grating Fabricated by a Micro-Patterned Liquid Crystal Polymer Phase Mask. Polymers, 9(8), 380. https://doi.org/10.3390/polym9080380