Groundwater Quality Assessment: An Improved Approach to K-Means Clustering, Principal Component Analysis and Spatial Analysis: A Case Study

Abstract

K-means clustering and principal component analysis (PCA) are widely used in water quality analysis and management. Nevertheless, numerous studies have pointed out that K-means with the squared Euclidean distance is not suitable for high-dimensional datasets. We evaluate a methodology (K-means based on PCA) for water quality evaluation. It is based on the PCA method to reduce the dataset from high dimensional to low for the improvement of K-means clustering. For this, a large dataset of 28 hydrogeochemical variables and 582 wells in the coastal aquifer are classified with K-means clustering for high dimensional and K-means clustering based on PCA. The proposed method achieved increased quality cluster cohesion according to the average Silhouette index. It ranged from 0.13 for high dimensional k-means clustering to 5.94 for K-means based on PCA and the practical spatial geographic information systems (GIS) evaluation of clustering indicates more quality results for K-means clustering based on PCA. K-means based on PCA identified three hydrogeochemical classes and their sources. High salinity was attributed to seawater intrusion and the mineralization process, high levels of heavy metals related to domestic-industrial wastewater discharge and low heavy metals concentrations were associated with industrial wastewater punctual discharges. This approach allowed the demarcation of natural and anthropogenic variation sources in the aquifer and provided greater certainty and accuracy to the data classification.

1. Introduction

Researchers use multivariate analysis to study the temporal and spatial characteristics of water quality [1,2,3,4,5,6,7,8]. Because current water quality assessment standards are not uniform and there are multiple and complex sources of water contamination, K-means clustering and principal component analysis (PCA) are widely used in water quality analysis and management [3,5,9,10]. Traditional clustering and PCA methodology for the evaluation of water quality is performed on the entire high dimensional hydrochemical dataset [3,9]. Clustering high dimensional data is the cluster analysis of data with anywhere from a few dozen to many thousands of dimensions. This approach allows identification of the significant characteristics or parameters that define the data structure by PCA and K-means allows the grouping of monitoring stations by similarities between the samples. Nevertheless, numerous studies have pointed out that K-means with the squared Euclidean distance is not suitable for high-dimensional data clustering because of dimensionality [11,12]. One alternative to solving this problem is to use alternative distance functions [13]. Another option to tackle this problem is to employ dimension reduction for high dimensional data. It is achieved apart from the traditional methods such as the Principal Component Analysis (PCA), with Multidimensional Scaling and Singular Value Decomposition [11,12].

The frequent problem in the application of cluster analysis is to decide an optimal number of clusters which suitably fit a data set. A significant advantage of the K-means algorithm is that it can evaluate the clustering results with the application of cluster validity indexes quantitatively and objectively, perceiving how many clusters are hidden in the dataset [11,14,15]. Cluster validity or clustering evaluation is formally defined as giving objective evaluations to clustering results in a quantitative way [16]. They are a necessary but challenging task in cluster analysis. It has even been stated that clustering validation be regarded as decisive as the clustering itself [11]. Every clustering algorithm will discover clusters even in a dataset that has no natural cluster structure. Indeed, cluster validity has become the core task of cluster analysis, for which a significant number of validation measures have been proposed and, with precision, analyzed in the literature [15]. Geographic information systems (GIS) can provide helpful tools for the manipulation and analysis of spatial information but is not complete for multivariate statistical and spatial studies [17]. The use of GIS as a visual tool allows the researcher to explore statistical outputs that would otherwise be difficult to interpret [18].

For the reasons previously mentioned, we present a methodology for water quality evaluation—called the K-means based on PCA method—to reduce the dataset from high dimensional to low for the improvement of K-means clustering in addition to spatial analysis (GIS). No systematic study into its benefits over traditional clustering methods has been performed. It allows the identification of the dominant hydrogeochemical processes controlling groundwater chemical composition and to achieve more comprehension of natural and anthropogenic sources influencing the spatial distribution of groundwater quality in the coastal aquifer Santo Domingo, Mexico.

2. Materials and Methods

2.1. Study Case: Santo Domingo Aquifer

The Valley of Santo Domingo (SD) is located in the state of Baja California Peninsula in Mexico and it lies between 24.9°36.1′30.3″ of latitude north and 111°23.8′26.8″ of longitude west (Figure 1). The SD Valley climate is arid, the mean annual temperature shows a broad span, between 1.9 °C and 43.3 °C. The average annual precipitation reaches only 150 mm, with minimum and maximum values of 50 and 300 mm/year, respectively [19]. The rainfall period occurs between July and September and the dry one from April to June. The annual evapotranspiration is 2270 mm/year, with maximum values of 370 mm/month [20]. The SD basin is the most extensive agricultural region in the Baja California Peninsula in Mexico. The agricultural extension covers an area of 72,409 ha, 49.4% of them are irrigated. During the agricultural period from 2013 to 2014 water withdrawals were 158,579 m³ [21].

2.2. Geology Setting

The geology of the Valley of Santo Domingo encloses two regional geological provinces: Purísima Sub-basin and The Giganta Volcanic Belt. The Purísima Sub-basin comprises Triassic sedimentary rocks and partially serpentized ultramafic rocks [22]. There are three main lithological formations included in the Purísima Sub-basin: Paleocene lutites from Santo Domingo Formation and Paleocene Eocene sandstone and lutite sequences of Tepetate Formation. The geological structure of the Purísima Sub-basin consists of a syncline around 600 km long, occupied by Upper Cretaceous to Lower Tertiary sediments [23].

The Giganta Volcanic Belt, located in the eastern region, is 500 km long by 30–50 km wide and comprises volcanic material as well as pyroclasts, lava flows and breccias, in addition to continental sand from the Comondú Formation [24]. The Salt Formation is widespread mainly in the central area. It is constituted by sand particles of quartz, feldspar and igneous rocks. The maximum thickness (185 m) is found in the northern region and it depends on the subsoil structure since the Quaternary sediments are assorted (fluvial, eolian and alluvial). Previous researchers reported high levels of carbonates in some aquifer zones, such as calcrete layers and a cementing material [24,25].

2.3. Hydrogeology Setting

The study area comprises part of three hydrographic basins: in the North by the Santo Domingo basin, in the middle part of the Las Bramonas watershed and to the South by the Santa Cruz basin [20,26]. It is defined as an unconfined granular aquifer composed principally of the Salts Formation and Quaternary sediments [27].

The distribution of hydraulic conductivity in the SD Basin is unequal. The amount of silt and clay in the Salt Formation increases towards the west, so a low hydraulic conductivity can be deduced.

In the SD Basin groundwater system, water flows from recharge areas in the western edge of the Sierra La Giganta Mountains towards the west in the Pacific Ocean [25].

In 1957, the elevation of the static water level in wells was above sea level (a.s.l.) in the entire SD Valley, whereas in 1996 the water level was 20 m a.s.l. in the direction of the east, but, in the center of the SD basin, the water level in wells was below mean sea level. Two local drawdown cones between 20 and 25 m below sea level (b.s.l.) are demarcated in the central area [25]. Previous studies in the 1980s reported high extractions reaching withdrawals of up to 450 Mm³/year (million m³ per year) and around 2.4 times the annual average recharge [25]. In the following years, the average annual recharge (188 Mm³) nearly equaled the extraction rate (168 Mm³) [26].

2.4. Water Sampling

Groundwater samples from 600 agricultural use wells (Figure 1) were collected at depths between approximately 16 m and 83 m between March and July 2010 in the aquifer area. Duplicate 250 mL polyethylene bottles were utilized; one contained HNO₃ added to 2 mL of 0.02 N for metals determination. The other sample was kept unacidified for anions and cations analysis [28,29].

2.5. Analytical Techniques

A total of 28 hydrogeochemical parameters were determined. The electrical conductivity (EC) was measured using a conductivity meter in units of deciSiemens (dS) (Model 162A, Thermo-Orion, Thermo Fisher Scientific, Waltham, MA, USA), and pH was measured with a pH meter (Metrohm E-632, Metrohm, Herisau, Switzerland) and the total dissolved solids (TDS) with a multi-parameter WTW (Wissenschaftlich-Technische-Werkstätten) (P3 MultiLine pH/LF-SET, Xylem Inc., Rye Brook, NY, USA).

Also, significant cations such as Ca²⁺, Mg²⁺, Na⁺ and K⁺ were determined by atomic absorption (AAS) and a flame photometer (Model: Systronics Flame Photometer 128, SYSTRONICS, Ahmedabad, India). A titration procedure determined the HCO₃⁻ concentration with H₂SO₄ and the Cl⁻ with AgNO₃, SO₄²⁻ and NO₃⁻ were measured by turbidimetry. Br⁻, B, F⁻ and PO₄³⁻ were determined with an automated flow injection analyzer (FIA) (Model: Quik Chem 8000, Lachat Instruments, Loveland, CO, USA). Trace metals concentrations (Al³⁺, Cd³⁺, Co²⁺, Cr³⁺, Cu²⁺, Fe³⁺, Li⁺, Mn²⁺, Ni²⁺, Pb²⁺, Sr²⁺ and Zn²⁺) were obtained by inductively coupled plasma optical emission spectroscopy (ICP-OES) (Mod-04 Lec-28, Shelton, CT, USA) [28]. The accuracy of the chemical analysis was validated by calculating charge balance errors (%CBE) with Equation (1):

$$\%CBE=\frac{{{\displaystyle \sum }}^{\text{}}cations-{{\displaystyle \sum }}^{\text{}}anions}{{{\displaystyle \sum }}^{\text{}}cations+{{\displaystyle \sum }}^{\text{}}anions}\times 100\%$$

(1)

where all cations and anions are specified as milliequivalents per liter. The ion balance errors for all groundwater samples ranged from −1.7 to 9%.

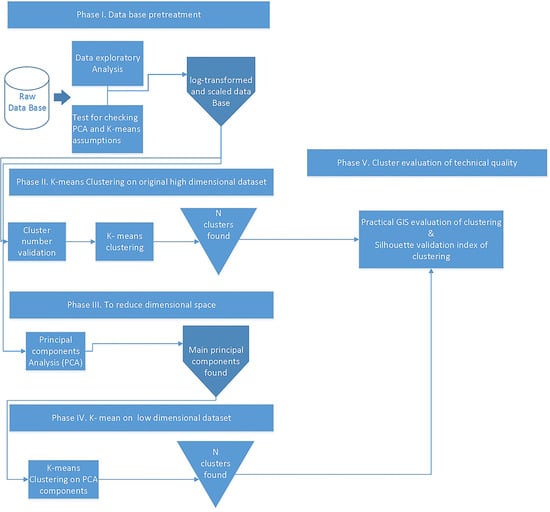
2.6. Multivariate Statistical Analysis

2.6.1. Research Approach

The approach used for this research involved five main components: Phase I Database pretreatment; Phase II K-means clustering on the original high dimension dataset; Phase III, to reduce dimensional space; Phase IV, K-means clustering on the low dimensional dataset; Phase V, cluster evaluation. The RStudio v. 1.0.153 (Copyright RStudio Inc., Boston, MA, USA) was utilized to perform descriptive statistics, study the distribution of the measured variables, the correlations matrix, perform the principal components analysis (PCA) and the cluster analysis (CA) (Figure 2).

2.6.2. Phase I Database Pretreatment

Eighteen wells exhibited incomplete data or were found to be outliers and they were removed from the original dataset (600 registers). Data that included values frequently lower than the detection limit of the method were excluded. When no recognition of ions was recorded, they were completed by the mean values of the neighboring data [30].

Most multivariate statistical methods require a log-normal data distribution. Therefore, the Kolmogorov-Smirnov (K-S) statistics were applied to test the goodness-of-fit of the data to a log-normal distribution. A 95% confidence log-normal distribution was obtained with a high significance level for all the parameters (p < 0.05) according to the K-S test [31].

Spearman’s rank was used to analyze the correlation between variables to account for the non-normal distribution of water quality parameters [32]. Kaiser Meyer Olkin (KMO) and Bartlett’s Sphericity statistics were performed to test the data accuracy and suitability for PCA, on the parameter correlation matrix. KMO is used to measure the sampling adequacy, which indicates the proportion of shared variance, that is, what might be caused by unknown factors. A high value (close to 1) commonly indicates that PCA may be useful as confirmative in this study (KMO 0.79). Bartlett’s test of Sphericity is employed to check the null hypothesis corresponding to uncorrelated variables [31]. It afforded a significance level less than 0.05, indicating excellent relationships among variables.

2.6.3. Phase II K-Means on the Original High Dimensional Dataset

The R package NbClust provided 24 indexes (Table S1) to determine the optimal number of clusters in a dataset [15]. The K-means algorithm based on within-cluster variation is a measure to form homogeneous clusters [14]. The clustering process starts with initial choosing observations and numbers the desired cluster to create initial centers—also called cluster centers—setting out from some initial values known seed-points. Each observation was placed randomly in a cluster to which it is closest, creating temporary clusters. K-means clustering was formulated as the sum of squared errors as is shown in the below equation [14,33,34]:

$$\mathrm{K}={\displaystyle \sum }_{l=1}^k{\displaystyle \sum }_{x\in C_l}{\left|\left|x-m_l\right|\right|}^2$$

(2)

where $X=\left\{x_1,\dots \dots \dots ,x_n\right\}$ is the data; $m_l={{\displaystyle \sum }}_{x\in C_l}\frac{x}{n_l}$ is known as the centroid of cluster $C_l, 1\le \mathrm{l}\le \mathrm{K}$; $n_l$ is the number of data objects in the cluster and $\mathrm{K}$ is the number of clusters.

The gravity centers of each temporary cluster are calculated and these become the new cluster centers. The data are partitioned randomly and iteratively reassigned to another cluster based on the nearest distance to the cluster’s center [14,33]. The procedure finishes when there is no reassignment to any data from one cluster to another [35].

2.6.4. Phase III to Reduce Dimensional Space

Principal Component Analysis (PCA) was employed to identify the most meaningful hydrochemical parameters.

The principal component (PC) approach is expressed as:

$$Z_{ij}=a_{i1}{x}_{1j}+a_{i2}{x}_{2j}+a_{i3}{x}_{3j}+\dots +a_{im}{x}_{mj}$$

(3)

where is the component score; $a$ is the component loading; $x$ is the measured value of the variable; $i$ is the component number, $j$ is the sample number and $m$ indicate the total number of variables [9,36]. Similar studies were successfully applied to assess water quality [3,36,37].

2.6.5. Phase IV K-Means Clustering on the Low Dimensional Dataset

We analyzed the efficiency of the K-means clustering in low-dimensional space. It was integrated by the reduced projected dataset ($\widehat{Y}$) into a new coordinate axis by applying $\widehat{W}$ to $X$.

$$\widehat{Y}=\widehat{W}X$$

(4)

where $\widehat{W}$ is the transformation matrix consisting of the most significant PC and $X$ is the matrix of the measured values. Its computational complexity is dominated by the M-step. The distance between each data point to all K centroids is computed: O(nKp), where n, K and p are the number of data points, the number of clusters and the dimension of the data, respectively. Thus, our approach utilizes this advantage because we work in the PCA subspace ($\widehat{Y}$) with a small dimensionality.

2.6.6. Phase V Cluster Evaluation of Technical Quality

Various measures are used to quantify the “goodness” of a cluster solution. In a good cluster solution, the elements within a cluster are similar to one (cohesive) while the clusters themselves are entirely different (separated) [38]. A popular measure is the silhouette coefficient, which is a measure of both cohesion and separation [39]. The silhouette measure varies from −1 to +1. In a good solution, the within-cluster distances are small and the between-cluster distances are extensive, resulting in a silhouette measure close to the maximum value of 1. Clusters obtained were contrasted with the spatial visualization of wells by ArcGIS v.10.3 (Copyright ESRI Inc., Redlands, CA, USA), to analyze the relationship between their characteristics and the activities on the surface.

2.7. Spatial Analysis and Modeling

The hydrochemical characterization of the 582 groundwater samples were assessed using the means of major cations (Ca²⁺, Mg²⁺, Na⁺, K⁺) and anions (Cl⁻, CO₃²⁻, HCO₃⁻, SO₄²⁻). The hydrochemical data were subjected to graphical treatment by plotting them in Piper´s Trilinear and using AquaChem v. 5.1 software (Copyright Waterloo Hydrogeologic, Waterloo, ON, Canada) and Stiff plots mapping was carried out using AquaChem v. 5.1 and ArcGIS v. 10.3. These methods were useful for understanding and identifying the water composition in different types.

3. Results and Discussion

3.1. Hydrochemical Analysis

Analysis of the 28 hydrochemical variables of groundwater in the study are presented in the descriptive statistical summary in

Table 1. Statistical summary of hydrochemical parameters of groundwater.

Parameter	Min	Max	Mean Value	S.D.
pH	6.40	8.78	8.10	0.31
TDS	326.40	5606.40	1285.10	765.79
EC	0.01	8.76	2.01	1.20
HCO3−	36.60	683.20	237.50	60.83
Cl−	42.54	2613.37	456.32	355.44
SO42−	2.73	325.73	29.23	34.53
Ca2+	4.41	731.26	109.46	99.20
Mg2+	11.79	238.50	64.68	42.46
K+	1.17	24.24	6.90	3.49
Na+	16.10	1051.10	194.00	126.50
NO3−	0.01	30.30	6.85	4.14
PO43−	0.001	4.27	0.03	0.23
B	0.18	5.00	0.50	0.43
Fe3+	0.001	5.06	0.23	0.56
Mn2+	0.001	0.33	0.01	0.02
F−	0.03	0.95	0.34	0.14
Br−	0.02	5.67	0.98	0.66
Li+	0.01	0.14	0.02	0.01
Sr2+	0.07	4.33	0.64	0.52
Cu2+	0.001	8.83	0.07	0.38
Zn2+	0.0004	0.53	0.02	0.04
Al3+	0.001	7.47	0.19	0.43
Cr3+	0.001	0.53	0.02	0.04
Ni2+	0.00	0.22	0.005	0.01
Pb2+	0.0002	0.49	0.02	0.02
Co2+	0.0002	0.08	0.01	0.0044
Cd3+	0.00002	0.003	0.0001	0.0004
S.W.L.	16.91	81.00	55.89	14.00

Note: Ion concentration (mg/L), pH (Standard Units), EC (∂S/m), TDS (mg/L). S.W.L. (Static Water Level in meters). S.D. indicates standard deviation.

. The water samples were slightly acidic to alkaline with pH values between 6.40 and 8.78 and electrical conductivity (EC) values ranging from 0.01 to 8.76 ∂S/m. Total dissolved solids (TDS) showed wide ranges of values from 326.4 to 5606.4 mg/L, with an average of 1285.10 and a standard deviation of 765.79 (Table 1), indicating wide variations in the concentrations of TDS attributed mainly to the seawater intrusion also reported in previous research [25]. Chloride concentrations with values ranging from 42.54 to 456.32 mg/L showed wide dissimilarities which are observed in the standard deviation of 355.44 (Table 1). Therefore Na⁺, Ca²⁺, HCO₃⁻, Mg²⁺ and SO₄²⁻ concentrations presented wide variations with standard deviations of 126.50, 99.20, 60.83, 42.46 and 34.53 respectively.

Table 2. Spearman’s rank correlation matrix for the groundwater quality data.

Variable	EC	TDS	Ca2+	Mg2+	Na+	K+	Cl−	SO42−	Br	Li	Sr	Zn	Cr	Static Level
EC	1
TDS	0.99	1
Ca2+	0.82	0.82	1
Mg2+	0.91	0.91	0.90	1
Na+	0.72	0.72	0.37	0.58	1
K+	0.46	0.46	0.36	0.38	0.49	1
Cl−	0.95	0.95	0.83	0.92	0.72	0.49	1
SO42−	0.77	0.77	0.61	0.75	0.66	0.28	0.72	1
Br	0.74	0.74	0.66	0.75	0.48	0.24	0.75	0.53	1
Li	0.65	0.65	0.71	0.63	0.35	0.28	0.66	0.38	0.57	1
Sr	0.84	0.84	0.85	0.84	0.53	0.55	0.85	0.57	0.69	0.80	1
Zn	−0.04	−0.04	−0.04	−0.03	0.01	−0.02	−0.02	−0.06	−0.02	−0.02	−0.03	1
Cr	−0.03	−0.03	−0.03	−0.02	0.00	−0.05	−0.02	−0.05	−0.01	−0.02	−0.03	0.92	1
Static water Level	0.04	0.04	0.11	0.01	−0.06	0.50	0.07	−0.13	0.03	−0.03	0.18	−0.04	−0.03	1

Note: Coefficients greater than 0.5 are underlined.

shows the main parameters obtained by the Spearman’s rank correlation matrix, from which can be observed a highly significant positive correlation of 0.90, 0.95, 0.92 and 0.82 between Ca²⁺ and Mg²⁺, Cl⁻ and TDS, Cl⁻ and Mg²⁺, in addition to Ca²⁺ and TDS respectively (Figure 3a–d). These demonstrate the significant contribution of these elements to the mineralization processes and salinization. Reference [40] studied variations in coastal aquifer groundwater and reported similar correlations (>0.9) between Cl⁻, Na⁺, Mg²⁺ and TDS.

A very high correlation (0.90) between Ca²⁺ and Mg²⁺ suggests the dissolution of calcite (CaCO₃) and dolomite CaMg(CO₃)₂ (Figure 3a) [41,42], the main component of sedimentary rocks, existing in these zones. High correlations of 0.92 and 0.83 between Cl⁻ with Mg²⁺ and Ca²⁺ (Figure 3e) and low correlations between HCO₃⁻ with Ca²⁺ and Mg²⁺ (Figure 3f) confirm that the salinization process is crucial in the aquifer [43]. A good correlation (0.85) between Sr²⁺ and Cl⁻ shows the aquifer mineralization process. Also, Br⁻ concentrations are well correlated with Cl⁻ and Mg²⁺ (0.75 and 0.75, respectively). These facts corroborate that their high levels are attributed to seawater intrusion in the aquifer.

Low concentrations of SO₄²⁻ with an average of 29.23 mg/L (Table 1) were observed throughout the aquifer. Despite NO₃⁻ levels being mostly within the maximum permissible limits [44,45], the highest values observed were between 20 and 30 mg/L. The NO₃⁻ boost could originated from agricultural and livestock activities when shallow static levels are present, allowing a direct infiltration of pollutants.

Therefore, high concentrations of Co²⁺, Cr³⁺, Cu²⁺, Fe³⁺, Mn²⁺, Ni²⁺ and Pb²⁺ (Table 1) were located near to urban and agricultural areas, these concentrations exceed the permissible values for drinking water [44] and irrigation [45] (Table S2 and Figure S1). Huge Cu²⁺ concentrations between 8.83 and 3.8 mg/L were observed nearby to settlements. High concentrations of Fe³⁺ between 3.2 and 4.2 mg/L also occur near urban areas. Moreover, critical levels of Pb²⁺ and Mn²⁺ (0.49 and 0.33 mg/L, respectively) are observed in the North and East. A high positive correlation of 0.92 between Cr³⁺ and Zn (Table 2) could indicate that industrial activities are its principal source.

3.2. Water Types

The hydrochemical data analysis of the samples was plotted using Piper’ Trilinear diagram (Figure S2). Also, the samples were plotted with a Stiff diagram and projected with ArcGIS v. 10.3 (Figure 4). Piper’s diagram is a suitable method to reveal the relations, dissimilarities and to classify water types based on the ionic composition of different groundwater samples [46].

The main water types were identified and categorized on the basis of significant ion concentrations, arranged in decreasing order of abundance, where the percentage reveals the amount of groundwater samples that fall into a water type. The Piper’s diagram shows that the main water types identified in the SD basin are mixed water types where these types cannot be recognized, due to neither anions nor cations being dominant, considering that no one cation−anion pair exceeds 50%.

3.2.1. Mixed of Ca²⁺-Mg²⁺-Na⁺-Cl⁻-HCO₃⁻ (38%)

The plot showed that 38% of the groundwater samples belong to mixed water of Ca²⁺-Mg²⁺-Na⁺-Cl⁻-HCO₃⁻. This water type covers the central and northeastern areas, in intermediate-depth wells between 30 to 60 m. It observed that this combined water is located nearby to SD and Bramonas rivers, irrigation canals and natural flow streams (Figure 4). The spatial location of wells suggests that this water class is related to urban, industrial and agricultural wastewater discharges in water bodies.

3.2.2. Mixed of Ca²⁺-Mg²⁺-Na⁺-Cl⁻ (30.8%)

The Piper´s diagram revealed that 30.8% of groundwater samples pertain to a combined water of Ca²⁺-Mg²⁺-Na⁺-Cl⁻. This water class includes the northern and western regions, where deep wells (60 to 80 m) are located near to settlements and shallow wells (16.91 to 30 m) occur nearby coastal zones (Figure 4). The spatial location of wells indicates that this water type is associated with wastewater discharge from anthropogenic sources and in addition to natural processes (intrusion seawater and mineral dissolution) in deep wells and shallow wells respectively.

3.2.3. Mixed of Na⁺-Mg²⁺-Cl⁻-HCO₃⁻ (13.7%)

The plot showed that only a few groundwater samples (13.7%) belong to mixed water of Na⁺-Mg²⁺-Cl⁻-HCO₃⁻. This water type covers most of the northern region, intermediate-depth wells between 30 and 60 m, generally located near agricultural zones and far from urban settlements (Figure 4). The spatial location of wells suggests that this water type is related to anthropogenic wastewater discharges from agricultural, industrial and urban activities. The results are similar to those reported in Reference [25].

3.3. K-Means Clustering on High Dimensional Dataset

Partition method K-means clustering was applied to a large dataset of 28 hydrogeochemical variables and 582 wells. Ten indexes from the R package NbClust suggested that wells are grouped in three clusters (See Table S3). Hence, further non-spatial and spatial analyses were performed based on this criterion.

The partition method K-means clustering, employed on a big dataset, resulted in three groups of wells. The spatial analysis showed high scattering among wells that belong to the same group (Figure 5). Wells within each group disclosed dissimilar hydrogeochemical characteristics. The cluster validity was carried out with the Silhouette index, which was from 0.13 as shown in Figure S3. Therefore, K-means clustering used on a large dataset revealed a grouping that was not suitable.

3.4. Principal Component Analyst (PCA)

Principal component analysis was used to decrease the dimensional space of the large dataset in order to improve the clustering. PCA considerably reduced 28 hydrogeochemical variables to 16 variables. PCA revealed that four components explain 71.6% of the total variance, with the salinization process and anthropogenic activities being the main factors controlling the groundwater quality variability. The PCA results are shown in

Table 3. Principal component and varimax rotated component matrix.

Variables	Component Matrix
	PC1	PC2	PC3	PC4	Communality
pH	0.155	0.147	0.360	0.110	0.187
TDS	−0.952	0.364	−0.043	−0.007	1.041
EC	−0.950	0.303	−0.033	−0.007	1.036
HCO3−	0.543	−0.030	−0.843	0.250	0.929
Cl−	−0.954	−0.059	−0.250	0.020	0.916
SO42−	−0.800	−0.121	−0.210	0.163	0.725
Ca2+	−0.819	0.197	0.112	−0.201	0.762
Mg2+	−0.843	0.285	−0.042	−0.057	0.797
K+	−0.203	−0.100	0.764	0.153	0.659
Na+	−0.864	−0.010	−0.323	0.302	0.888
NO3−	−0.081	0.047	−0.399	−0.293	0.254
Fe3+	−0.134	−0.187	0.120	0.768	0.658
Mn2+	−0.238	−0.053	0.142	0.896	0.883
Cu2+	0.310	0.865	−0.039	0.018	0.846
Zn2+	0.201	0.794	−0.033	−0.164	0.698
Cr3+	0.216	0.910	−0.049	−0.141	0.897
Pb2+	0.059	0.792	−0.029	0.010	0.631
Static water level	0.372	−0.044	0.823	−0.137	0.836
Eigen values	6.113	3.311	2.414	1.804
Variability (%)	33.96	16.553	12.072	9.021
Cumulative (%)	33.96	50.514	62.586	71.607

Note: A Rotation method: varimax with Kaiser normalization.

. The PCA approach identified four components that have the most critical loading (Figure 6).

3.4.1. PCA1

The first component (PCA1) explains 33.96% of the total variance and encompasses the following main ions: Cl⁻ (0.95), TDS (0.95), EC (0.95), Na⁺ (0.86), Mg²⁺ (0.84), Ca²⁺ (0.82) and SO₄²⁻ (0.80) were strongly related (Table 3 and Figure 6). The significant variables (Na⁺, Mg²⁺, Ca²⁺, SO₄²⁻, Cl⁻ TDS and EC) within PCA1 followed the same direction and showed a major increase related to salinity. PCA1 demonstrates that the salinization process is the main factor controlling the groundwater quality variability and the importance of mineralization process. Natural processes such as seawater intrusion, cations exchange, calcite dissolution, dolomitization and sulfate reduction occur and they are increased by anthropogenic activities. Other researchers reported assessed water quality in coastal aquifers and found the same parameters representativeness TDS, Cl⁻, Na⁺, Mg²⁺, SO₄²⁻ and Ca²⁺ as PCA1 with 42.30% [2,10,40].

3.4.2. PCA2

The second component (PCA2) explains 16.55% of the total variance and was assembled by Cr³⁺ (0.91), Cu²⁺ (0.86), Pb²⁺ (0.79) and Zn (0.79), showing high correlations among themselves toward the same direction (Table 3). The main variables (Cr³⁺, Cu²⁺, Pb²⁺ and Zn²⁺) within PCA2 demonstrated an increase caused by metal pollution in the Valley (Figure 6). High concentrations occur near urban areas and small settlements. In this component, the primary cause of pollution is industrial activity. Furthermore, this process is reinforced by the high levels of Cl⁻ in the aquifer through Chloride complexation. This process makes metal mobility in the aquifer easy [47].

3.4.3. PCA3

The third component (PCA3) accounts for 12.07% of the total variance and describes the significant contributions of HCO₃⁻ (−0.84), K⁺ (0.76) and the static water level (0.82) (Table 3 and Figure 6), disclosing good correlations among themselves. PCA3 revealed an inverse correlation between HCO₃⁻ and the static water level, demonstrating that when increasing the static water level, concentrations of HCO₃⁻ decrease. High concentrations of HCO₃⁻ are found in shallow wells. Commonly, K⁺ concentrations in aquifers are low (<10 mg/L); otherwise, external sources overcome the permitted limit [48,49]. The high K⁺ concentrations (10 to 24.24 mg/L) occur in urban areas and near agricultural zones. This result indicates that domestic wastewater discharges and potassium fertilizers are essential sources (Figure 7).

3.4.4. PCA4

The fourth component (PCA4) explains 9.02% of the variance and shows the highest correlation between Mn²⁺ (0.89) Fe³⁺ and (0.76) (Table 3 and Figure 6), conducted toward the same direction. Both elements are naturally simultaneous and PCA4 stated the same source for Fe³⁺ and Mn²⁺ ions. Higher concentrations are observed near the urban areas; they could be released to the environment by any industrial and domestic wastewater punctual discharge, as there is no mining activity in the zone.

3.5. K-Means Clustering on Low Dimensional Dataset

The low dimensional dataset was obtained by Equation (4), where $\widehat{W}$ is the matrix of the main four PCs found and $X$ is the matrix of values observed and ($\widehat{Y}$) is the matrix of transformed data (582 X 4). We realized K-means clustering on a low dimensional dataset and showed significant improvement in the grouping. K-means clustering on a low dimensional dataset was achieved to increase quality cluster cohesion according to an average Silhouette index. The index ranged from 0.13 (Figure S3) for high dimensional K-means clustering to 5.94 (Figure S4) for K-means based on PCA. Both groupings were projected spatially for practical evaluation. K-means based on PCA clustered samples with similar hydrogeochemical characteristics, showing higher quality results (Figure 8 and

Table 4. Statistics of the three categories found from the K-means clustering analysis.

Parameter	Class 1 (n = 160)					Class 2 (n = 166)					Class 3 (n = 256)
	Min	Max	Mean	Median	S.D.	Min	Max	Mean	Median	S.D.	Min	Max	Mean	Median	S.D.
pH	6.40	8.38	7.85	7.84	0.24	7.14	8.78	8.21	8.21	0.32	6.97	8.78	8.18	8.15	0.26
TDS	6.40	5606.40	2169.94	1926.40	883.22	326.40	998.40	671.77	665.60	130.56	576.00	2035.20	1126.48	1100.80	280.38
EC	0.01	8.76	3.39	3.01	1.38	0.51	1.56	1.05	1.04	0.20	0.90	3.18	1.76	1.72	0.44
HCO3−	85.40	683.20	235.29	228.14	71.91	131.76	475.80	247.56	244.00	54.45	36.60	500.20	232.45	231.80	56.44
Cl−	141.80	2613.37	872.41	754.02	409.32	42.54	384.99	169.31	170.16	53.60	192.49	811.45	380.81	357.69	117.91
SO42−	4.64	325.73	57.07	40.32	51.97	2.89	35.91	11.15	9.22	6.65	2.73	99.23	23.50	19.32	16.51
Ca2+	46.89	731.26	217.96	183.57	123.91	4.41	129.06	43.51	40.48	21.20	16.83	257.71	83.81	76.25	40.77
Mg2+	18.58	238.50	116.16	107.77	41.84	11.79	61.11	29.14	28.37	9.60	17.62	123.44	55.35	53.22	19.79
K+	1.95	24.24	9.18	8.60	4.23	1.17	9.78	4.55	4.30	2.03	1.96	15.25	6.98	7.04	2.63
Na+	80.50	1051.10	287.90	239.20	185.26	16.10	264.50	119.84	112.70	44.62	66.70	533.60	183.21	174.80	67.49
NO3−	0.01	29.60	8.38	7.41	4.93	0.43	30.30	6.83	5.90	4.10	0.37	23.70	5.90	5.17	3.26
PO43−	0.001	2.49	0.03	0.01	0.20	0.002	4.27	0.06	0.02	0.39	0.001	0.19	0.02	0.01	0.02
B	0.18	3.47	0.01	0.42	0.55	0.18	5.00	0.005	0.36	0.44	0.19	2.45	0.005	0.37	0.30
Fe3+	0.002	4.13	0.29	0.07	0.65	0.003	3.82	0.23	0.05	0.54	0.001	5.06	0.20	0.04	0.52
Mn2+	0.001	0.11	0.01	0.01	0.01	0.001	0.06	0.01	0.01	0.01	0.001	0.33	0.01	0.01	0.02
F−	0.091	0.66	0.30	0.30	0.10	0.11	0.95	0.39	0.38	0.15	0.03	0.76	0.34	0.34	0.13
Br−	0.04	5.67	0.02	1.61	0.73	0.02	2.86	0.005	0.45	0.29	0.24	2.30	0.01	0.88	0.39
Li+	0.01	0.14	0.03	0.03	0.01	0.01	0.03	0.02	0.02	0.00	0.01	0.04	0.02	0.02	0.01
Sr2+	0.29	4.33	0.01	1.10	0.62	0.07	0.68	0.003	0.25	0.09	0.13	1.50	0.01	0.50	0.19
Cu2+	0.001	0.66	0.07	0.07	0.11	0.001	8.83	0.13	0.07	0.70	0.001	0.65	0.04	0.07	0.05
Zn2+	0.0004	0.45	0.02	0.02	0.05	0.001	0.53	0.02	0.02	0.04	0.001	0.30	0.02	0.01	0.02
Al3+	0.001	1.22	0.17	0.19	0.15	0.001	7.47	0.25	0.19	0.67	0.002	4.76	0.16	0.12	0.35
Cr3+	0.001	0.45	0.02	0.02	0.04	0.001	0.53	0.02	0.02	0.04	0.001	0.30	0.02	0.02	0.02
Ni2+	0.001	0.22	0.01	0.00	0.02	0.001	0.05	0.004	0.002	0.01	0.001	0.12	0.01	0.01	0.01
Pb2+	0.0002	0.09	0.02	0.02	0.01	0.001	0.49	0.02	0.02	0.04	0.001	0.14	0.02	0.02	0.01
Co2+	0.0002	0.08	0.01	0.01	0.01	0.001	0.01	0.01	0.01	0.001	0.001	0.07	0.01	0.01	0.005
Cd3+	0.00002	0.0029	0.0001	0.00002	0.0005	0.00002	0.002	0.00005	0.00002	0.0002	0.00002	0.003	0.0001	0.00002	0.0004
S.W.L.	16.91	77.105	54.69	61.01	16.67	17.76	74.76	52.39	54.09	12.54	21.18	81.00	58.89	61.28	12.91

Note: Ion concentration (mg/L), pH (Standard Units), EC (∂S/m), TDS (mg/L). S.W.L. signal static level (meters). S.D. indicates standard deviation. n indicate number wells by cluster.

).

3.5.1. First Class: 160 Wells

Dominant parameters are EC, TDS, Cl⁻, Ca²⁺, K⁺ and Na⁺ with average values of 3.39, 2169.94, 872.41, 217.96, 9.18 and 287.90 respectively (See Table 4). The groundwater class is mostly affected by salinity, caused by different factors such as the mineralization process, seawater intrusion, industrial and urban wastewater discharges, infiltration of leachates from open dumps and poorly designed sanitary landfills, fertilizer application and water over pumping in deep wells. Deep wells are located near to urban and agricultural areas while shallow wells are proximate to coastal zones (see red zones in Figure 8).

For example, high concentrations of K⁺ are observed mainly in class 1 (Figure 7a) and could be attributed to domestic and agricultural wastewater discharges. Groundwater samples from class 1 and class 3 collected from wells belong to agricultural and livestock zones and urban zones (Figure 8). Smaller concentrations of K⁺ showed in class 2 (Figure 7a) due to the fact that pollutants do not reach distant zones. Water samples from class 2 were collected from regions further away from settlements and agricultural activities.

3.5.2. Second Class: 166 Wells

Groundwater quality is perturbed by metals such as Al³⁺, Cr³⁺, Co²⁺, Cu²⁺, Fe³⁺, Pb²⁺ and Zn²⁺ with average values of 0.02, 0.01, 0.13, 0.23, 0.02 and 0.02 mg/L respectively (Table 4 and Figure 7b).

Figure 7b shows high concentrations of Al³⁺, Pb²⁺, Cu²⁺ and Cr³⁺ in class 2. Industrial and domestic wastewater are poured into drainage irrigation canals and natural flow streams and cause damage [50]. Wells have intermediate depths, located near channels and flow streams such as Bramonas and the Santo Domingo rivers (see yellow zones in Figure 8).

3.5.3. Third Class: 256 Wells

Class 3 has better water quality and therefore it is less influenced by industrial and domestic wastewater discharges. The slight increases of 0.01, 0.01, 0.01 and 0.02 mg/L (Table 4) in ion concentrations such as Co²⁺, Mn²⁺, Ni²⁺ and Pb²⁺ respectively could be attributed to industrial wastewater punctual discharges and agriculture and natural geological conditions. Deeper wells are mainly dedicated to agricultural irrigations and are located in this zone (see orange zones in Figure 8).

3.6. Discussion

K-means clustering based on PCA allows the finding of the location of 160 wells (class 1). Shallow wells are located mainly in coastal zones and deep wells are located in urban and agricultural areas of the aquifer. They are related to variables highly significant for PCA1 (TDS, EC, Cl⁻, Na⁺, Mg²⁺, Ca²⁺ and SO₄²⁻) and PCA3 (HCO₃⁻, K⁺ and static level). High concentrations of these species found in wells belong to class 1 and class 3 respectively. The water quality of the wells is related to the salinization process and seawater intrusion, the primary source controlling the groundwater quality variability in the aquifer.

The K-means algorithm grouped 166 wells (class 2) near to drainage irrigation canals and flow streams. They were linked to the significant variables of PCA2 (Cu²⁺, Zn²⁺ and Cr³⁺) and PCA4 (Fe³⁺). High levels of these ions observed in wells belong to class 2 and class 1 respectively. In these wells, the water quality influenced by heavy metals sourced from industrial and domestic wastewater poured into surface streams.

The third class includes 250 wells (class 3) located mainly in agricultural zones in the center and north aquifers. They correlated with the variables of PCA2 (Pb²⁺ and Zn²⁺) and PCA4 (Mn²⁺). High concentrations of these species found in wells belong to class 3. In this group of wells, the primary source influencing the groundwater quality is the location of industrial wastewater punctual discharges. Class 3 has better water quality than classes 1 and 2.

In addition to the previous results, the improved method (K-means clustering based on PCA) allowed definition of the characteristics and hydrogeochemical processes of the aquifer. The determination of hydrogeochemistry is essential for establishing a conceptual model and distinguishing the natural processes of an aquifer. However, the factors that affect hydrochemistry are mainly controlled by stochastic processes, so they vary in time and space. For these reasons, the sources of variation must identify for the correct determination of the hydrogeochemical model. In this case study, there is excellent spatial coverage, 600 wells distributed throughout the aquifer. However, little attention is paid to temporal variation, so the analysis does not allow us to analyze the temporal factors that cause variation in water quality, such as a change due to randomness (storm, rainfall) and changes due to climatic seasons (temperature, rainfall). Therefore, these monitoring systems show a static but excellent spatial representation of the hydrochemical structure of the aquifer and allow us to analyze the principal sources of variability by cross-referencing with the spatial distribution of water quality.

4. Conclusions

The proposed method achieved improvement of the cluster cohesion Silhouette index ranging from 0.13 for high dimensional k-means clustering to 5.94 for K-means clustering based on PCA and practical spatial GIS evaluation of clustering indicated high-quality results for K-means based on PCA.

K-means clustering based on PCA identified three hydrogeochemical classes and their sources. High salinity was attributed to seawater intrusion and mineralization process, high levels of heavy metals related to domestic-industrial wastewater discharge and low heavy metals concentrations were associated with industrial wastewater punctual discharges. This approach allowed the demarcation of natural and anthropogenic variation sources in the aquifer and provided greater certainty and accuracy of the data classification.

Three hydrochemical classes of groundwater were identified. The first class (Cluster 1): Shallow wells and deeper wells consistent with proximity to the coast and urban zones respectively. This class of water was associated with high salinity, which comes from seawater intrusion and the mineralization process. The second class (Cluster 2): Intermediate and deep wells located in urban-industrial zones and settlements. This type of water correlated with high concentrations of heavy metals, which it could attribute to domestic-industrial wastewater discharge in drains and flow streams. The third class (Cluster 3): Deeper wells located mainly in agricultural and urban areas. This water-type related to a slight increase in some heavy metals, which was attributed to industrial wastewater punctual discharges.

The proposed method showed a static but excellent spatial representation of the hydrochemical structure of the aquifer and allowed us to analyze the principal sources of variability by cross-referencing with the spatial distribution of water quality. The improved method could be applied to optimize sampling and to schemes monitoring groundwater quality.