Hydrological Performance and Runoff Water Quality of Experimental Green Roofs
Abstract
:1. Introduction
2. Material and Methods
2.1. Experimental Model
2.2. Data Collection-Runoff and Water Quality
2.3. Modelling of the Runoff
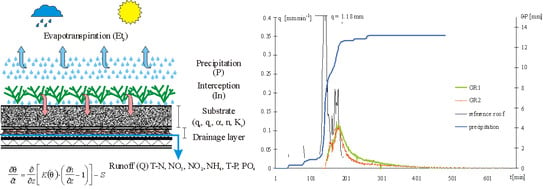
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Conflicts of Interest
References
- Carpenter, C.M.G.; Todorov, D.; Driscoll, C.T.; Montesdeoca, M. Water quantity and quality response of a green roof to storm events: Experimental and monitoring observations. Environ. Pollut. 2016, 218, 664–672. [Google Scholar] [CrossRef] [PubMed]
- Castigla, R.; Wilkinson, S. Modelling green roof stormwater response for different soil depths. Landsc. Urban Plan. 2016, 153, 170–179. [Google Scholar] [CrossRef]
- Claessens, L.; Hopkinson, C.; Rastetter, E.; Vallino, J. Effect of historical changes in land use and climate on the water budget of an urbanizing watershed. Water Resour. Res. 2006, 42, W03426. [Google Scholar] [CrossRef]
- MacAvoy, S.E.; Plank, K.; Mucha, S.; Williamson, G. Effectiveness of foam-based green surfaces in reducing nitrogen and suspended solids in an urban installation. Ecol. Eng. 2016, 91, 257–264. [Google Scholar] [CrossRef]
- Razzaghmanesh, M.; Beecham, S.; Kazemi, F. Impact of green roofs on stormwater quality in a South Australian urban environment. Sci. Total Environ. 2014, 470–471, 651–659. [Google Scholar] [CrossRef] [PubMed]
- Zhang, B.; Li, N.; Wang, S. Effect of urban green space changes on the role of rainwater runoff reduction in Beijing, China. Landsc. Urban Plan. 2015, 140, 8–16. [Google Scholar] [CrossRef] [Green Version]
- Zhang, Q.; Miao, L.; Wang, X.; Liu, D.; Zhu, L.; Zhou, B.; Sun, J.; Liu, J. The capacity of greening roof to reduce storm water runoff and pollution. Landsc. Urban Plan. 2015, 144, 142–150. [Google Scholar] [CrossRef]
- Jurik, L.; Huska, D.; Halaszova, K.; Bandlerova, A. Small water reservoirs—Sources of water or problems? J. Ecol. Eng. 2015, 16, 22–28. [Google Scholar] [CrossRef]
- Berndtsson, J.C. Green roof performance towards management of run-off water quantity and quality: A review. Ecol. Eng. 2010, 36, 351–360. [Google Scholar] [CrossRef]
- Dunnet, N.; Kingsbury, N. Planting Green Roofs and Living Walls; Timber Press: Portland, OR, USA, 2004. [Google Scholar]
- Fassman-Beck, E.; Voyde, E.; Simcock, R.; Hong, Y.S. 4 Living roofs in 3locations: Does configuration affect runoff mitigation? J. Hydrol. 2013, 490, 11–20. [Google Scholar] [CrossRef]
- Zhang, Z.; Szota, K.; Fletcher, T.D.; Williams, N.S.G.; Werdin, J.; Farrell, C. Influence of plant composition and water use strategies on green roof stormwater retention. Sci. Total Environ. 2018, 625, 775–781. [Google Scholar] [CrossRef] [PubMed]
- Stovin, V.; Vesuviano, G.; Kasmin, H. The hydrological performance of a green roof test bed under UK climatic conditions. J. Hydrol. 2012, 414–415, 148–161. [Google Scholar] [CrossRef]
- Versini, P.A.; Ramier, D.; Berthier, E.; de Gouvello, B. Assessment of the hydrological impacts of green roof: From building scale to basin scale. J. Hydrol. 2015, 524, 562–575. [Google Scholar] [CrossRef] [Green Version]
- Buccola, N.; Spolek, G. A pilot-scale evaluation of green roof runoff retention, detention, and quality. Water Air Soil Pollut. 2011, 216, 83–92. [Google Scholar] [CrossRef]
- Hilten, R.N.; Lawrence, T.M.; Tollner, E.W. Modeling stormwater run-off from green roofs with HYDRUS-1D. J. Hydrol. 2008, 358, 288–293. [Google Scholar] [CrossRef]
- Nardini, A.; Andri, S.; Crasso, M. Influence of substrate depth and vegetation type on temperature and water runoff mitigation by extensive green roofs: Shrubs versus herbaceous plants. Urban Ecosyst. 2012, 15, 697–708. [Google Scholar] [CrossRef]
- Palla, A.; Gnecco, I.; Lanza, L.G. Unsaturated 2D modelling of subsurface water flow in the coarse-grained porous matrix of a green roof. J. Hydrol. 2009, 379, 193–204. [Google Scholar] [CrossRef]
- She, N.A.; Pang, J. Physically based green roof model. J. Hydrol. Eng. 2010, 15, 458–464. [Google Scholar] [CrossRef]
- Herrera, J.; Flamant, G.; Gironás, J.; Vera, S.; Bonilla, C.A.; Bustamante, W.; Suárez, F. Using a Hydrological Model to Simulate the Performance and Estimate the Runoff Coefficient of Green Roofs in Semiarid Climates. Water 2018, 10, 198. [Google Scholar] [CrossRef]
- Soulis, K.; Valiantzas, J.; Ntoulas, N.; Kargas, G.; Nektarios, P. Simulation of green roof runoff under different substrate depths and vegetation covers by coupling a simple conceptual and a physically based hydrological model. J. Environ. Manag. 2017, 200, 434–445. [Google Scholar] [CrossRef] [PubMed]
- Voyde, E.; Fassman, E.; Simcock, R. Hydrology of an extensive living roof under sub-tropical climate conditions in Auckland, New Zealand. J. Hydrol. 2010, 394, 384–395. [Google Scholar] [CrossRef]
- Wang, X.; Tian, Y.; Zhao, X. The influence of dual-substrate-layer extensive green roofs on rainwater runoff quantity and quality. Sci. Total Environ. 2017, 592, 465–476. [Google Scholar] [CrossRef] [PubMed]
- Wong, G.K.; Jim, C. Quantitative hydrologic performance of extensive green roof under humid-tropical rainfall regime. Ecol. Eng. 2014, 70, 366–378. [Google Scholar] [CrossRef]
- Yio, M.H.N.; Stovin, V.; Werdin, J.; Vesuviano, G. Experimental analysis of green roof substrate detention characteristics. Water Sci. Technol. 2013, 68, 1477–1486. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Mentens, J.; Raes, D.; Hermy, M. Green roofs as a tool for solving the rainwater runoff problem in the urbanized 21st century? Landsc. Urban Plan. 2006, 77, 217–226. [Google Scholar] [CrossRef]
- Speak, A.F.; Rothwell, J.J.; Lindley, S.J.; Smith, C.L. Rainwater runoff retention on an aged intensive green roof. Sci. Total Environ. 2013, 461, 28–38. [Google Scholar] [CrossRef] [PubMed]
- Burszta-Adamiak, E.; Mrowiec, M. Modeling of green roofs hydrologic performance using EPA’s SWMM. Water Sci. Technol. 2013, 68, 36–42. [Google Scholar] [CrossRef] [PubMed]
- Simunek, J.; Sejna, M.; Saito, H.; Sakai, M.; van Genuchten, M.T. The HYDRUS-1D Software Package for Simulating the One-Dimensional Movement of Water, Heat, and Multiple Solutes in Variably Saturated Media; Version 4.16; Department of Environmental Sciences, University of California Riverside: Riverside, CA, USA, 2013. [Google Scholar]
- Palla, A.; Gneco, I. Hydrologic modeling of low impact development system at the urban catchment scale. J. Hydrol. 2015, 528, 361–368. [Google Scholar] [CrossRef]
- Karczmarczyk, A.; Bus, A.; Baryła, A. Phosphate Leaching from Green Roof Substrates—Can Green Roofs Pollute Urban Water Bodies? Water 2018, 10, 199. [Google Scholar] [CrossRef]
- Pęczkowski, G.; Orzepowski, W.; Pokładek, R.; Kowalczyk, T.; Żmuda, R.; Wójcik, R. Właściwości retencyjne zielonych dachów typu ekstensywnego na przykładzie badań modelowych. Acta Sci. Pol. Formatio Circumiectus 2016, 15, 113–120. [Google Scholar] [CrossRef]
- Šimůnek, J.; van Genuchten, M.T. Modeling Nonequilibrium Flow and Transport Processes Using HYDRUS. Vadose Zone J. 2008, 7, 782–797. [Google Scholar] [CrossRef]
- Wosten, J.H.M.; Van Genuchten, M.T. Using texture and other soil properties to predict the unsaturated soil hydraulic conductivity. Soil Sci. Soc. Am. J. 1988, 52, 1762–1770. [Google Scholar] [CrossRef]
- Mualem, Y. A new model for predicting the hydraulic conductivity of unsaturated porous media. Water Resour. Res. 1976, 12, 513–522. [Google Scholar] [CrossRef]
- Moriasi, D.N.; Arnold, J.G.; Van Liew, M.W.; Bingner, R.L.; Harmel, R.D.; Veith, T.L. Model evaluation guidelines for systematic quantification of accuracy in watershed simulations. Am. Soc. Agric. Biol. Eng. 2007, 50, 885–900. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Liesecke, H.J. Extensive begrunung bei 50 dachneigung. Stadt und Grun 1999, 48, 337–346. [Google Scholar]
- Scholz-Barth, K. Green Roofs: Stormwater Management from the Top Down; Environmental Design & Construction: Washington, DC, USA, 2001. [Google Scholar]
- Fassman, E.A.; Simcock, R.; Voyde, E. Extensive Green (Living) Roofs for Stormwater Mitigation. Part 1: Design and Construction; Techincal Report, TR2010/017; Auckland Regional Council: Auckland, New Zealand, 2010.
- Metselaar, K. Water retention and evapotranspiration of green roofs and possible natural vegetation types. Resour. Conserv. Recycl. 2012, 64, 49–55. [Google Scholar] [CrossRef]
- Teemusk, A.; Mander, Ü. The Influence of Green Roofs on Runoff Water Quality: A Case Study from Estonia. Water Res. Manag. 2011, 25, 3699–3713. [Google Scholar] [CrossRef]
- Harper, G.E.; Limmer, M.A.; Showalter, W.E.; Burken, J.G. Nine-month evaluation of runoff quality and quantity from an experiential green roof in Missouri, USA. Ecol. Eng. 2015, 78, 127–133. [Google Scholar] [CrossRef]
- Kuoppamäki, K.; Hagner, M.; Lehvävirta, S.; Setälä, H. Biochar amendment in the green roof substrate affects runoff quality and quantity. Ecol. Eng. 2016, 88, 1–9. [Google Scholar] [CrossRef]







| Measurement | Unit | Substrate of Zeolite GR1 | Substrate of Pumice GR2 |
|---|---|---|---|
| Bulk density | g·cm−3 | 0.97 | 0.69 |
| Specific Density | g·cm−3 | 1.85 | 1.28 |
| Water drainage of soil | mm | 19.5 | 20.7 |
| Coefficient water drainage | % | 17.7 | 18.8 |
| Water holding capacity | mm | ||
| pF 0 | 52.7 | 50.7 | |
| pF 2.0 | 32.0 | 31.2 | |
| pF 3.0 | 27.6 | 27.2 | |
| pF 4.2 | 15.1 | 14.0 |
| Substrate | θr | θs | α (m·m−1) | n (−) | Ks (mm·min−1) |
|---|---|---|---|---|---|
| substrate with zeolite | 0.04 | 0.479 | 0.0038 | 1.529 | 8.1 |
| substrate with pumice | 0.02 | 0.461 | 0.0045 | 1.553 | 12.2 |
| Rainfall Event | Rain Depth (mm) | Peak of Rain Intensity (mm·min−1) | Rain Duration (min) | Retained Volume (%) | Flow Peak (mm·min−1) | Peak Reduction (%) | Initial Moisture (% v/v) | ||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| GR1 | GR2 | GR1 | GR2 | GR1 | GR2 | GR1 | GR2 | ||||
| 28.04 | 20.7 | 0.12 | 676 | 68.2 | 76.3 | 0.09 | 0.08 | 25.0 | 33.3 | 14.1 | 8.9 |
| 30.05 | 18.5 | 1.8 | 248 | 17.9 | 28.3 | 0.9 | 0.86 | 50.0 | 52.2 | 16.3 | 10.8 |
| 6.06 | 14.8 | 0.22 | 523 | 73.4 | 82.1 | 0.1 | 0.11 | 54.5 | 50.0 | 14.7 | 8.3 |
| 27.06 | 15.3 | 0.48 | 371 | 63.5 | 72.3 | 0.37 | 0.35 | 22.9 | 27.1 | 17.1 | 11.1 |
| 28.06 | 16.7 | 2.25 | 190 | 57.0 | 59.8 | 1.01 | 0.96 | 55.1 | 57.3 | 14.3 | 6.7 |
| 29.06 | 11.0 | 0.19 | 420 | 81.0 | 89.6 | 0.12 | 0.11 | 36.8 | 42.1 | 29.0 | 26.6 |
| 10.07 | 50.1 | 2.36 | 97 | 33.2 | 65.4 | 1.12 | 1.05 | 52.5 | 55.5 | 23.0 | 13.9 |
| 23.07 | 16.4 | 1.44 | 194 | 16.9 | 27.6 | 0.99 | 1.0 | 31.2 | 30.5 | 25.0 | 14.7 |
| 24.07 | 39.5 | 5.7 | 613 | 9.8 | 11.2 | 5.10 | 2.90 | 10.5 | 49.1 | 37.6 | 34.1 |
| 25.07 | 16.2 | 0.56 | 425 | 27.5 | 32.7 | 0.47 | 0.39 | 16.1 | 30.3 | 28.1 | 19.8 |
| 28.07 | 26.6 | 2.4 | 144 | 79.1 | 84.1 | 0.114 | 0.113 | 90.0 | 90.0 | 36.0 | 32.1 |
| 11.08 | 13.5 31.0 | 2.47 4.97 | 94 46 | 67.1 74.6 | 93.8 89.7 | 2.20 1.35 | 0.77 0.83 | 11.9 72.8 | 68.8 82.3 | 18.9 21.9 | 11.8 19.1 |
| 1.09 | 47.2 | 0.52 | 1145 | 91.4 | 95.6 | 0.26 | 0.22 | 50.0 | 57.6 | 17.1 | 9.7 |
| 11.09 | 10.9 | 0.16 | 429 | 72.3 | 77.1 | 0.11 | 0.09 | 31.2 | 43.7 | 30.0 | 23.1 |
| 23.09 | 15.1 | 0.21 | 711 | 69.9 | 98.1 | 0.17 | 0.15 | 19.0 | 28.6 | 33.1 | 26.4 |
| 22.10 | 13.3 | 0.22 | 183 | 66.9 | 71.5 | 0.15 | 0.13 | 31.8 | 40.9 | 34.3 | 32.8 |
| 29.10 | 21.1 | 1.55 | 651 | 7.3 | 32.8 | 1.30 | 0.86 | 16.2 | 44.5 | 36.0 | 30.8 |
| Event Date (dd/mm) | GR1 | GR2 | ||
|---|---|---|---|---|
| NSE (−) | ME (mm·min−1) | NSE (−) | ME (mm·min−1) | |
| 28/04 | 0.77 | 0.11 | 0.70 | 0.09 |
| 30/05 | 0.75 | 0.18 | 0.71 | 0.11 |
| 6/06 | 0.80 | 0.21 | 0.77 | 0.18 |
| 27/06 | 0.78 | 0.22 | 0.70 | 0.20 |
| 28/06 | 0.81 | 0.10 | 0.69 | 0.093 |
| 29/06 | 0.77 | 0.09 | 0.61 | 0.06 |
| 10/07 | 0.85 | 0.23 | 0.43 | 0.1 |
| 23/07 | 0.79 | 0.14 | 0.72 | 0.12 |
| 24/07 | 0.70 | 0.17 | 0.65 | 0.15 |
| 25/07 | 0.70 | 0.17 | 0.68 | 0.15 |
| 11/08 | 0.83 | 0.12 | 0.80 | 0.11 |
| 1/09 | 0.84 | 0.08 | 0.80 | 0.06 |
| 11/09 | 0.88 | 0.092 | 0.77 | 0.05 |
| 23/09 | 0.82 | 0.10 | 0.79 | 0.09 |
| 22/10 | 0.77 | 0.11 | 0.75 | 0.10 |
| 29/10 | 0.73 | 0.05 | 0.55 | 0.12 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pęczkowski, G.; Kowalczyk, T.; Szawernoga, K.; Orzepowski, W.; Żmuda, R.; Pokładek, R. Hydrological Performance and Runoff Water Quality of Experimental Green Roofs. Water 2018, 10, 1185. https://doi.org/10.3390/w10091185
Pęczkowski G, Kowalczyk T, Szawernoga K, Orzepowski W, Żmuda R, Pokładek R. Hydrological Performance and Runoff Water Quality of Experimental Green Roofs. Water. 2018; 10(9):1185. https://doi.org/10.3390/w10091185
Chicago/Turabian StylePęczkowski, Grzegorz, Tomasz Kowalczyk, Katarzyna Szawernoga, Wojciech Orzepowski, Romuald Żmuda, and Ryszard Pokładek. 2018. "Hydrological Performance and Runoff Water Quality of Experimental Green Roofs" Water 10, no. 9: 1185. https://doi.org/10.3390/w10091185
APA StylePęczkowski, G., Kowalczyk, T., Szawernoga, K., Orzepowski, W., Żmuda, R., & Pokładek, R. (2018). Hydrological Performance and Runoff Water Quality of Experimental Green Roofs. Water, 10(9), 1185. https://doi.org/10.3390/w10091185