An Ensemble Decomposition-Based Artificial Intelligence Approach for Daily Streamflow Prediction

Abstract

Accurate prediction of daily streamflow plays an essential role in various applications of water resources engineering, such as flood mitigation and urban and agricultural planning. This study investigated a hybrid ensemble decomposition technique based on ensemble empirical mode decomposition (EEMD) and variational mode decomposition (VMD) with gene expression programming (GEP) and random forest regression (RFR) algorithms for daily streamflow simulation across three mountainous stations, Siira, Bilghan, and Gachsar, in Karaj, Iran. To determine the appropriate corresponding input variables with optimal lag time the partial auto-correlation function (PACF) and auto-correlation function (ACF) were used for streamflow prediction purpose. Calibration and validation datasets were separately decomposed by EEMD that eventually improved standalone predictive models. Further, the component of highest pass (IMF1) was decomposed by the VMD approach to breakdown the distinctive characteristic of the variables. Results suggested that the EEMD-VMD algorithm significantly enhanced model calibration. Moreover, the EEMD-VMD-RFR algorithm as a hybrid ensemble model outperformed better than other techniques (EEMD-VMD-GEP, RFR and GEP) for daily streamflow prediction of the selected gauging stations. Overall, the proposed methodology indicated the superiority of hybrid ensemble models compare to standalone in predicting streamflow time series particularly in case of high fluctuations and different patterns in datasets.

1. Introduction

Developing an efficient predictive technique for both long- and short-term streamflow is a challenge in hydrology which is crucial for resource planning and management. This is because streamflow is influenced by various dynamic nonlinear processes, such as rainfall, runoff yield and confluence, evaporation, topography, and anthropic activities (e.g., [1]). In addition, streamflow forecasting has attracted more attention because of reservoir operations and irrigation management decisions. Over the past decades, researchers have carried out different attempts to forecast monthly streamflow. Streamflow forecasting models consist of two general categories: process-driven and data-driven. Process-driven models are based on empirical formulas that focus on principal physical processes of the hydrological cycle [2].

However, AI models which are fundamentally “black-box” avoid analyzing the physical processes. In other words, these models are more user-friendly and can be used without accurate knowledge of the physical mechanisms of the watershed system [3]. Thus, AI modeling has been widely used for streamflow forecasting in recent years because of the availability of long-term gauging data, the ever-increasing computational power. For example, Chitsaz et al. [4] proposed a pre-processing based model to forecast monthly streamflow. They considered three data-driven models, generalized regression neural network (GRNN), multi-layer perceptron (MLP), and adaptive neuro fuzzy inference system (ANFIS) and pre-processing techniques, such as principal component analysis (PCA), singular value decomposition (SVD) and average values of inputs for their aims. The results revealed that SVD highly improved forecasting values and was effective as a pre-processing method in hydrological simulation. A hybrid technique was presented by Humphrey et al. [5] which integrated hydrological model outputs (GR4J conceptual rainfall–runoff model) into a Bayesian artificial neural network to forecast streamflow. The results indicated that hybrid models outperform the standalone models, particularly in term of high flows. Another attempt was conducted by Abdollahi et al. [6] to predict daily mean streamflow of perennial and non-perennial rivers in semi-arid region of Zagros Mountains in Iran using standalone and hybrid models. The applicability of proposed models was evaluated applying several performance metrics. They concluded that gene expression programming (GEP) integrating wavelet transform (WT) was the most accurate in predicting streamflow. Yuan et al. [1] investigated the accuracy of hybrid long short-term memory (LSTM) for which its parameters were optimized by the ant lion optimizer (ALO) algorithm in forecasting the monthly streamflow. The results proved that the historical monthly streamflow was predicted more accurately when using LSTM-ALO compared to other models. Mehr [7] presented an integrated predictive model for streamflow forecasting in intermittent streams. He implemented the GEP model combined genetic algorithm (GA) in which sub-expression trees of the best evolved GEP model were rescaled by appropriate weighting coefficients through the use of GA optimizer. The optimum input variables were identified by auto-correlation and partial auto-correlation functions of the streamflow records. The outcomes showed that the GEP based genetic algorithm outperforms genetic programming, GEP, multiple linear regression and GEP-linear regression as benchmarks models.

In computer science, AI is demonstrated by machines, in contrast to the natural intelligence represent by animals and humans. In recent years, AI techniques have been increasingly used to solve a large number of environmental and water engineering problems. These include evolutionary polynomial regression (EPR) [8,9], ANFIS [10,11], gene expression programming (GEP) [12,13], model tree (MT) [14,15], support vector machine (SVM) [16,17,18], and extreme learning machine (ELM) [8,19]. Various researches have also used AI approaches particularly for river flow forecasting [20,21,22,23,24]. However, developing a sophisticated model to forecast flow is a challenge since many (nonlinear) factors control rainfall–runoff processes in the catchment. Thereby, using the raw data for modeling directly may not provide permissible results, but applying a pre-processing method may improve model performance [25].

Recently, a vast number of data pre-processing methods have been developed, such as continuous wavelet transform (CWT) [8,26], maximum entropy spectral analysis (MESA) [27], wavelet multi-resolution analysis (WMRA) [28], PCA [29,30], singular spectrum analysis (SSA) [31,32], and moving average (MA) [33], which enhanced model predictability. Moreover, noise-assisted data analysis method namely ensemble empirical mode decomposition (EEMD) have been pioneered by Wu and Huang [31]. It is an advanced form of the traditional decomposition approach (e.g., wavelet and Fourier decompositions), and is an empirical, intuitive, and self-adaptive data processing method developed for non-stationary, nonlinear, and signal sequences [34]. The VMD is another non-stationary signal decomposition technique which is presented to overcome the lack of exact mathematical model [35,36,37].

Many EEMD and variational mode decomposition (VMD) based algorithms have been applied in hydrology to predict rainfall and runoff records [38,39,40,41]. The work of Napolitano et al. [42] was the first attempt in using artificial neural networks (ANNs) based on EEMD for daily streamflow prediction. In the sequel, Wang et al. [43] coupled EEMD-SVM approach as an adaptive data analysis method with particle swarm optimization to decompose annual rainfall time series records for annual streamflow prediction. Soon after, Li et al. [44] proposed a hybrid prediction model based on VMD-ELM to improve the capability of the monthly precipitation prediction model.

Appling the hybrid approaches for daily streamflow forecasting has reached enormous popularity since it takes the advantages of different methods. Consequently, the purpose of this study was to employ two-phase decomposition based random forest algorithm and gene expression programming for daily streamflow prediction at three stations, Siira, Bilghan, and Gachsar, in Karaj basin, Iran. This work is one of the first attempts known to the authors that used the ensemble empirical mode decomposition as the primary decomposition technique, to enhance the prediction of daily streamflow records with random patterns and fluctuations. So, to diminish noise, trend, and stochastic behaviors of the data, an additional decomposition approach (i.e., VMD) is proposed and incorporated. This additional decomposition procedure is an iterative process. The proposed integrated models are benchmarked and evaluated with standalone models (GEP and random forest regression (RFR)) using several well-established performance’s criteria. Finally, the diagnostic analyses are adopted to show how daily streamflow forecasting of the ensemble decomposition based models can improve model fidelity more intuitively.

The rest of the present research has been organized as follows: Section 2.1 to Section 2.4, the methodology of EEMD and original forecasting models (i.e., GEP and RFR) are introduced. Section 2.5 and Section 2.6 include a description of the applied statistical performance benchmarks and uncertainty analysis for evaluating model performance. Section 2.7 describes the data and study areas. Section 3 compares the results of the proposed models, and finally in Section 4, a summary and conclusion is provided.

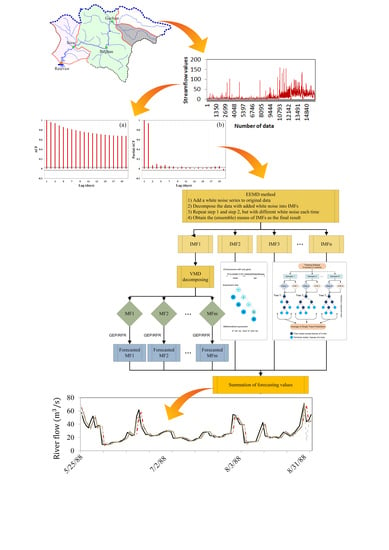
2. Methodology and Data Description

2.1. Gene Expression Programming

One of the most common AI models is GEP, which is inspired by Darwin’s theory and developed form of genetic programming technique. GEP evolves computer programing in different forms consisting decision trees and logical and mathematical expressions [45,46,47]. Moreover, the GEP approach has high performance in solving a large number of problems in different fields especially water engineering [48,49,50,51]. Here, mathematical equations based on the GEP model have been applied to predict daily streamflow records in Karaj basin, Iran. Gene expression programming is coded as linear chromosomes, which is represented in form of expression trees (ETs). In point of fact, ETs are complicated computer programs which are evolved for solving practical problems and are determined based on their fitness at solving those problems. The corresponding mathematical expressions can also be extracted from these tree structures. An ETs population can discover traits. Hence, it will adapt to the specific problem which they are used to solve [46]. GEP development involves five steps. Determine the fitness function (fi) for each individual program (i) is the first step, which is computed as:

$$f_i={\displaystyle \sum }_{j=1}^{C_i}\left(M-\left|C_{\left(i,j\right)}-T_j\right|\right)$$

(1)

where M, T_j, and C_(i,j) are, respectively, the range of selection range, the maximum value for fitness case j, and provided value using the individual chromosome i in fitness case j. Second, the function and terminals set are determined for chromosomes generating. It should be noted that peer reviewing the prior investigations is necessary to find a suitable function set. Hence, in this study, several basic operators (+, −, ×, /) and mathematical functions (√, power, exp) have been employed to model daily streamflow data. Third, the chromosomal architecture is configured. The liking function and the genetic operator’s sets are selected in the fourth step and case variation and their rate are determined in the final step. Figure 1a illustrates a simple tree representation of classical GEP. More details about GEP and its architecture have been provided in the various literatures, such as Ferreira [46] and Shahrara et al. [13].

2.2. Random Forest Regression

RFR is a state-of-the-art hierarchical algorithm proposed by Breiman [52] that computes the appropriate relationship between input and output parameters. It is a learning algorithm of tree-based ensemble, which during the model building process, raises various decision trees and each of them in the ensemble model is trained by bootstrapped sample of the main input dataset. The output estimation values are then computed using the average of these estimation trees. The proposed RFR approach is illustrated in Figure 1b with a specific algorithmic procedure introduced by Svetnik et al. [53] and Cootes et al. [54] as follows:

(1)

Use the original training dataset X (N samples) to draw k samples randomly by the bootstrap resampling technique to construct k regression trees. In this process, the probability related to the samples that would not be drawn can be computed by $p = {\left(1-1/N\right)}^N$. If N achieved to infinity, p ≈ 0.37 which expresses that roughly 37% of the samples of original training dataset X are not drawn and these data are known as out-of-bag (OOB) data. Likewise, the training dataset, these OOB data can be applied for testing samples.

(2)

Moreover, unpruned regression trees corresponding to k bootstrap samples are created. During the growing process of trees, in each node, a attribute is randomly considered from all A attributes (input parameters) as internal nodes (a < A). Then, based on the principle of minimum Gini index (a measure of how each variable contributes to the homogeneity of the nodes and leaves), an optimum attribute is determined from an attribute as a split variable to build the branches hierarchy.

(3)

The final random forest regression model is constituted by generated k regression trees. To evaluate the model estimation performance, two indices namely coefficients of determination ($R_{RFR}^2$) and mean square error of OOB (MSE_OOB) are employed.

$$MS{E}_{OOB}=\frac{{{\displaystyle \sum }}_{i=1}^n{\left(y_i-{\widehat{y}}_i\right)}^2}{n}$$

(2)

$$R_{RFR}^2=1-\frac{MS{E}_{OOB}}{{\widehat{\sigma }}_y^2}$$

(3)

where n is the total OOB samples, y_i and ŷ_i are the observed and predicted output values, respectively, and ${\widehat{\sigma }}_y^2$ is the OOB variance of predicted output.

2.3. Ensemble Empirical Mode Decomposition

EEMD as an improvement of EMD is a type of mathematical function and data pre-processing technique which represents a non-stationary and nonlinear signal from original dataset, expressed by Wu and Huang [31]. One of the EEMD features is decomposing the signals of the original dataset to a small and the finite length of oscillatory modes according to the local properties’ time scales [55]. The oscillatory modes are described by components of intrinsic mode functions (IMFs) where embedded in the data. EMD is a self-adaptive time-frequency approach, without elementary information about the nature that its IMF indicates a signal as a sum of mean zero well-behaved both slow and fast oscillation modes related to IMFs given by two principles [31,55]. These include: (i) the number of extrema and zero-crossings must either be equal or at least different from one throughout the whole length and (ii) for every point, the mean value of the local minimum and maximum envelope is equal to zero. Generally, an IMF indicates a simple oscillatory mode in comparison with the simple harmonic function. According to the definition, a shifting process of original daily streamflow time series dataset can be briefly described throughout six steps as stressed by Huang et al. [55].

Step 1: Determine all local minima and maxima (extrema) points of a given time series y(t);

Step 2: Connect local extrema points for forming the bottom and upper envelopes (e_max(t) and e_min(t)) with spline interpolation, respectively;

Step 3: Determine the mean m(t) between two maxima and minima envelopes as follow:

$$m\left(t\right)=\left(e_{max}\left(t\right)+e_{min}\left(t\right)\right)/2$$

(4)

Step 4: Diminish the average value m(t) from the data to determine an IMF candidate as follow: $h\left(t\right)= y\left(t\right)- m\left(t\right)$.

Step 5: If h(t) meets two IMF properties based on the predefined stopping benchmarks, h(t) is defined as the first IMF (written as c₁(t) which 1 is its index); else, y(t) is replaced with h(t) and repeat steps 1 to 4 until h(t) meet the two IMF properties.

Step 6: The residual r₁(t) = y(t) − c₁(t) is defined as new dataset subjected to the same shifting proceeding as explained for other IMFs from r₁(t). In this step, the shifting processing can be ceased, if the r(t) has a steady trend or has a local extrema point from no IMF may be provided [56]. Finally, in this method, the y is created from the aggregation of intrinsic mode functions and residual as:

$$y\left(t\right)={\displaystyle \sum }_{i=1}^n{c}_i\left(t\right)+r_n\left(t\right)$$

(5)

where n is the IMF number, r_n(t) is the final r(t), and c_i(t) are closely orthogonal together, and all of them have mean zero. More informative about the EMD technique and the ceasing benchmarks have been provided by Huang et al. [55,56]. Hence, evaluations show EMD is still unstable because of the mode mixing [31]. Mode mixing is defined as either a single IMF including a wide range of disparate scales components or a similar scale component residing in various IMFs [57]. For overcoming the mode mixing problem in EMD, the EEMD is modified as an improved technique. Regarding this argument, the whole space of time-frequency becomes uniformly filled by adding the white noise which can simplify a normal divorce of the frequency scales and decay the mode mixing event.

2.4. Variational Mode Decomposition

The main aim of this study is developing and investigating a two-layer integrated predictive approach. Therefore, variational mode decomposition (VMD) as a pre-processing technique for signal decomposition was applied [58]. The VMD algorithm has an ability in decomposing a signal x(t) to K discrete sub-signals number. The VMD is employed as a constrained optimization issue, expressed by Dragomiretskiy and Zosso [58]:

$$f=\begin{array}{c}min\\ \left\{U_k\right\},\left\{{\omega }_k\right\}\end{array}\left\{{\displaystyle \sum }_k\Vert {\partial }_t\left[\left(\delta \left(t\right)+\frac{j}{\pi t}\right)\times U_k\left(t\right)\right]e^{-j{\omega }_{k}t}{\Vert }_2^2\right\}subjectto{\displaystyle \sum }_k{U}_k$$

(6)

where $\left\{U_k\right\}:\left\{U_1,U_2,\dots ,U_K\right\}$ and $\left\{{\omega }_k\right\}:\left\{{\omega }_1,{\omega }_2,\dots ,{\omega }_K\right\}$ indicate stenography, impression related to all modes set and their central frequency, respectively. Moreover, δ(t) and × denotes the Dirac distribution and convolution, respectively. So, the Lagrangian multipliers and term of quadratic penalty are defined to convert this constrained optimization issue to an unconstrained problem [38]:

$$\begin{array}{cc}\hfill L\left(\left\{U_k\right\},\left\{{\omega }_k\right\},\lambda \right)& =\alpha \left\{{\displaystyle {\displaystyle \sum }_k}\Vert {\partial }_t\left[\left(\delta \left(t\right)+\frac{j}{\pi t}\right)\times U_k\left(t\right)\right]e^{-j{\omega }_{k}t}{\Vert }_2^2\right\}+\Vert f\left(t\right)-{\displaystyle {\displaystyle \sum }_k}{U}_k\left(t\right){\Vert }_2^2\hfill \\ & +\langle \lambda \left(t\right),f\left(t\right)-{\displaystyle {\displaystyle \sum }_k}{U}_k\left(t\right)\rangle \hfill \end{array}$$

(7)

Equation (7) can be resolved with alternative approaches. In this way, Equation (7) has been shown as two stages,

(1) $U_k$ Minimization:

$${\widehat{U}}_k^{n+1}=\frac{\widehat{f}\left(\omega \right)-{{\displaystyle \sum }}_{i\ne k}{\widehat{U}}_i\left(\omega \right)+\frac{\widehat{\lambda }\left(\omega \right)}{2}}{1+2\alpha {\left(\omega -{\omega }_k\right)}^2}$$

(8)

(2) ${\omega }_k$ Minimization:

$${\omega }_k^{n+1}=\frac{{{\displaystyle \int }}_0^{\infty }\omega {\left|{\widehat{U}}_k\left(\omega \right)\right|}^{2}d\omega }{{{\displaystyle \int }}_0^{\infty }{\left|{\widehat{U}}_k\left(\omega \right)\right|}^{2}d\omega }$$

(9)

where ${\widehat{U}}_i\left(\omega \right)$, ${\widehat{U}}_k^{n+1}$, $\widehat{f}\left(\omega \right)$, $\widehat{\lambda }\left(\omega \right)$ indicate the Fourier transform of $U_i\left(\omega \right)$, $U_k^{n+1}$, f(ω), λ(ω), respectively, and n is the iterations number. The use of VMD diminishes remaining noises in the modes and avoids the redundant modes compared to EEMD approach. Moreover, VMD decomposes a multi-elements signal to some mode functions of the quasi-orthogonal intrinsic [59]. During VMD and EEMD combination, resolving the patterns of low frequency which exist in the IMF1 signal is the main goal of applying different AI methods. This helps the model to be more responsive to the patterns of the fine-scale dataset that is important for simulating inconsistencies in the dataset.

2.5. Model Assessment Criteria

Several standard statistical criteria are used in the present research for evaluating the performance of the modeled and observed streamflow. In addition to common criterion, such as root mean square error (RMSE), Nash–Sutcliffe efficiency (NSE), and mean absolute error (MAE), the indices below were applied to assess the fidelity of predicted model.

• Ratio of RMSE to standard deviation (RSD): RSD, proposed by Singh et al. [60] is a model evaluation metric to assess the differences between a model’s prediction and the observed data in hydrological simulation. This metric is calculated based on RMSE and standard deviation (STDEV) of the observed data points. The lower the value of the RSD the higher the performance of the model.

  $$\mathrm{RSD}=\frac{\mathrm{RMSE}}{{\mathrm{STDEV}}_{obs}}=\frac{\left[\sqrt{{{\displaystyle \sum }}_{i=1}^N{\left(Q_{obs}-Q_{for}\right)}^2}\right]}{\left[\sqrt{{{\displaystyle \sum }}_{i=1}^N\left(Q_{obs}-\overline{Q_{obs}}\right)}\right]}$$

  (10)
• Uncertainty at 95% (U95): U95 is defined as a 95% uncertainty confidence.

  $$U_{95}=1.96\sqrt{\left({\mathrm{STDEV}}^2+{\mathrm{RMSE}}^2\right)}$$

  (11)
• Reliability of model (%): This statistic shows the satisfactory state of the model’s forecast by the probability [19].

  $$Reliability= \frac{{{\displaystyle \sum }}_{i=1}^N{K}_i}{N}\times 100\%$$

  (12)

  $$K_i=\{\begin{array}{c}1, if\left(RA{E}_i\le \delta \right)\\ 0, else\end{array}$$

  (13)

  $$RA{E}_i=\frac{\left|Q_{for}\left(i\right)-Q_{obs}\left(i\right)\right|}{Q_{obs}\left(i\right)}\times 100\%, RA{E}_i \ge 0$$

  (14)
• Resilience of model (%): This indicator defines how quickly the model forecast is likely to recover once an unqualified forecast has occurred [61].

  $$Resilience=\{\begin{array}{c}100\%, if (Reliability=100\%)\\ \frac{{{\displaystyle \sum }}_{i=1}^{N-1}{R}_i}{N-{{\displaystyle \sum }}_{i=1}^N{K}_i}\times 100\%, else\end{array}$$

  (15)

  $$R_i=\{\begin{array}{c}1, if (RA{E}_i>\delta and RA{E}_{i+1}\le \delta )\\ 0, else\end{array}$$

  (16)

  where $Q_{obs}$ and $Q_{for}$ denote the measured and estimated values, respectively; $\overline{Q_{obs}}$ is the average of observed values, and N is the number of datasets. RAE_i is the value for the ith data, K_i is the number of times that the threshold value (δ) of the qualified forecast is greater than or equal to the RAE value. δ is set to 20% according to the Chinese standard (GB/T 22482-2008). R_i is the number of times that model forecast is likely to transfer from unqualified into qualified forecast in the ith data.

2.6. Uncertainty Analysis

A quantitative evaluation of the uncertainty in streamflow prediction is carried out using standalone and hybrid models. The uncertainty analysis is used to validate the dataset for each gauging stations. It should be noted that daily streamflow time series may contain uncertainty. For example, errors in streamflow data resulting from uncertainty in the stage-flow rating curve may affect the simulation results. This happens especially during repeated rainfall events when the measured values are extrapolated outside the range of the established rating curve [62]. In this study, a quantitative uncertainty evaluation of streamflow predicting rate E is computed by using EEMD-VMD based GEP and RFR models. The uncertainty analysis is performed for lag values of daily streamflow. The individual error of prediction Equation (17) is computed for all datasets to compute mean ($\overline{\mathit{e}}$) and standard deviation ($S_e$) of estimating error using Equations (18) and (19) [63].

$$e_i={\log }_{10}\left(Q^{pre}{}_i\right)-{\log }_{10}\left(Q^{obs}{}_i\right)$$

(17)

$$\overline{\mathit{e}}={\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}{e}_i$$

(18)

$$S_e=\sqrt{{\displaystyle \sum }_{\mathit{i}=\mathbf{1}}^{\mathit{n}}\left(\frac{{\left(e_i-\overline{e}\right)}^{\mathbf{2}}}{n-1}\right)}$$

(19)

where n is the number of datasets, and positive and negative mean forecasting error values represent, respectively, overestimation and underestimation of measured flow. To this end, a band of confidence is expressed around forecasted error values by the Wilson score method [64]. In addition, using $\pm 1.96S_e$ gives about 95% confidence band surrounding predicted $P_i$ as follow:

$$\{P_i\times {10}^{-\overline{\mathit{e}}-1.96S_e},P_i\times {10}^{-\overline{\mathit{e}}+1.96S_e}\}$$

(20)

2.7. Case Study and Data Analysis

Iran is mostly an arid region with 242 mm annual precipitation which is equal to one third of the annual average precipitation of the world [65]. Thus, the surface water resources are not sufficient to meet all demand, and, therefore, consumers have been tapping into groundwater resources. Tehran is the capital and the most populated city in Iran where about 340 × 10⁶ m³ of its water demands are supplied from the Karaj reservoir located on Karaj River in Varian Strait 23 km from the city of Karaj (Figure 2) [66]. Karaj reservoir with an area of approximately 764 km² was constructed in the period from 1957 to 1961 to supply drinking water for Tehran residents, hydroelectric power production, and irrigation of the Karaj plain [67].

Karaj drainage system is located between 52°2′ to 51°32′ E and 35°52′ to 36°11′ N with an area of 850 km² and a circumference of 146 km on the southern portion of Alborz mountain range. Average annual flow for Karaj Dam is 472 million cubic meters. The maximum elevation of the watershed is about 4200 m, and the lowest is 1600 m. The average daily discharge is estimated at 154.54 m³/s. In this study, three hydrometric stations were selected, namely Gachsar, Bilghan, and Siira. Details of datasets and the parameters used for the proposed models are given in

Table 1. Descriptive statistics of river flow data for the study site located at the Karaj basin.

Station	Crd	El (m)	Xmin (m3/s)	Xmax (m3/s)	Xmean (m3/s)	Sx	Cv	Csx
Siira	36°01′ N 51°09′ E	1898	0	160	11.8	12.54	157.35	2.64
Bilghan	36°00′ N 51°17′ E	2138	0	194	15.81	14.04	197.17	3.21
Gachsar	36°06′ N 51°19′ E	2258	0	61	3.93	3.99	15.96	2.34

Crd, El, X_min, X_max, X_mean, S_x, C_v, and C_sx denote the coordinates, elevation, minimum flow, maximum flow, mean flow, standard deviation, variation coefficient, and skewness coefficient, respectively.

.

In addition, Figure 3a–c display the frequency of observed daily streamflow records using normal fit distribution to show the distribution of data by forming bins along the range of the data and then drawing bars to show the number of observations that fall in each bin. The histograms of the streamflow for all three stations follow a bell shape and indicate that the time series records follow a normal distribution. Time series data for Siira, Bilghan, and Gachsar stations were available, respectively, since 1954–1998, 1947–1993, and 1982–2001. These datasets were used to calibrate the proposed models. 1999–2008, 1994–2008, and 2001–2008 were used for validation.

3. Results and Discussion

A hybrid ensemble model (e.g., EEMD-VMD-GEP and EEMD-VMD-RFR) is first coded and implemented to forecast daily streamflow with a long time dataset series at the three selected gauging stations. To achieve more reliable and accurate model, outliers which may be recorded by a faulty device, typos, etc., are identified and replaced with the average of previous and subsequent reliable records. The results of each model were then computed and evaluated by several model performance metrics in the calibration and validation periods. For better understanding, the results of the three stations have been evaluated separately which have been discussed below.

3.1. Input Variables Selection and Model Development

To simulate daily streamflow records in the selected stations, a lag time was applied to each station to define the appropriate dataset that correspond to the streamflow records at the outlet. We applied a partial auto-correlation function (PACF) and an auto-correlation function (ACF) value to the time series to determine the corresponding datasets. Figure 4 represents the ACF and PACF analyses of the daily streamflow data for each application. Based on this analysis, three lags of 1 to 7, 6, and 4 days are considered, respectively, for Siira, Bilghan, and Gachsar gauging stations. That is, the values of lag (red lines in Figure 4) which are upper or lower than ±1.96/$\sqrt{n}$ should be considered as the effective input variables for streamflow forecasting.

The monotonic trends in daily streamflow are analyzed by Spearman’s rank correlation test which is one of the nonparametric techniques and quantitatively assessed how strongly the two data sets are related to each other. This approach with uniform power for linear and non-linear trends is widely applied to verify the absence of trends. In the present study, the null hypothesis of the analysis is that two variables are independent and identically distributed (iid) and the alternative hypothesis is that increasing or decreasing trends may exist. As demonstrated in

Table 2. Values of the correlation coefficient between the daily streamflow and the individual input variables.

Station	Parameter Value	Input Variable
		Qs(t−1)	Qs(t−2)	Qs(t−3)	Qs(t−4)	Qs(t−5)	Qs(t−6)	Qs(t−7)
Siira	R	0.97**	0.95**	0.94**	0.92**	0.89**	0.86**	0.82**
	P-value	0.00	0.00	0.00	0.00	0.002	0.005	0.008
Bilghan	R	0.97**	0.95**	0.93**	0.91**	0.88**	0.84**	-
	P-value	0.00	0.00	0.00	0.001	0.002	0.004	-
Gachsar	R	0.95**	0.92**	0.88**	0.82**	-	-	-
	P-value	0.00	0.00	0.002	0.006	-	-	-

** Correlation is significant at the 0.05 level.

, correlations between the output (present streamflow) and input (antecedent values of streamflow) variables for all three stations are evaluated by the Spearman’s rank correlation test which is performed using SpSS-18. Furthermore, P values <0.05 are selected as the confidence level for the correlation test.

Spearman’s rank correlation coefficients for the input variables at three stations are more than 0.8, and the P-values are less than 0.05 (confidence level). Therefore, the null hypothesis that the two populations are independent is rejected at a level of significance of 5 % and the output variable (daily streamflow) is judged to be dependent on input variables.

Furthermore, one of the important analyses that confirms that the hydrological time series are not affected by non-climatic factors, such as station environment, station location, observation practices, and instruments, is the homogeneity test. In hydro–climatological studies, this non-parametric test is considered as a critical quality control method to detect the variability of climatology dataset [68]. Generally speaking, having completely homogeneous data due to non-climatic causes that occur by the changes in the time-series and the obvious nonstationarity in the study area (changes in metadata, etc.) surrounding a meteorological station can be disregarded as neglectable.

Therefore, the temporal homogeneity of time-series is required in hydrological modeling. In this regard, the homogeneity of the streamflow data in three hydrometric stations is analyzed using two absolute homogeneity tests, the Neumann ratio test and Pettitt test, that are mostly used in the hydro–climate nonstationary test [68,69,70,71]. The annual mean as the testing variable is considered in Siira, Bilghan, and Gachsar flow stations because of the presence of the missing values on daily streamflows. The streamflow series of each station were computed for a significance level of 0.05. The annual quantities of the testing variables under the null hypothesis are independent, and the series is assumed as homogeneous. On the other hand, Pettitt test assumes the series consisted of a break in the mean and are considered as inhomogeneous, while the Von Neumann ratio test assumes that the series is not randomly distributed under the alternative hypothesis.

As defined in

Table 3. Results of homogeneity tests for annual mean streamflow records.

Station	Pettitt Test			Van Neumann Test
	P-value	Statistics	Class	P-value	Statistics	Class
Siira	0.462	252	A	0.006	2.38	A
Bilghan	0.69	240	A	0.026	1.74	A
Gachsar	0.133	92	A	0.02	1.52	A

Critical values for Pettitt test are <306, <318, and <95, and Von Neumann test are <1.57, <1.59, and <137, respectively, for the Siira, Bilghan, and Gachsar stations.

, the null hypothesis of the homogeneity analyses for annual mean streamflow at three stations is not rejected at 5% level of significance for the Pettitt and Van Neumann tests. Based on the criteria presented by Wijngaard et al. [71], the results are placed into the three groups (class A: (useful) zero or one rejection; class B: (doubtful) two rejections; and class C: (suspect) three or more rejections). From Table 3, all three stations fall under class A (useful) and can be used for further analysis.

For developing a two-phase hybrid, EEMD-VMD-based GEP and RFR models, streamflow records are divided into calibration (approximately 75% of the whole dataset) and validation datasets (reminder of whole dataset). Both calibration and validation datasets were, respectively, decomposed into different components of IMFs. To pre-process the data, a residual value which computes the details of high and low flow frequencies in the data was then included as the model input data series. This helped to pre-process the data and eliminate trend and pattern in time series. The decomposition of the dataset into nine IMFs and one residual component is illustrated in Figure 5.

Due to high fluctuations of oscillatory in the first IMF (IMF1), a secondary VMD-IMF1 decomposition was carried out. It should be noted that the number of intrinsic modes determination plays a vital role in the VMD process because it can define appropriately resolved time-series data for a permissible prediction model. If this process does not proceed, the specification of the hidden original time series dataset cannot be provided fully which may result in a lower component. Conversely, a large number of intrinsic modes can cause a poor performance leading to the influences of error accumulation from each prediction module in the aggregation stage as seen elsewhere [72].

Notwithstanding the above necessity, the intrinsic modes given by the VMD algorithm may be smoother compared to decomposed components by other traditional techniques, such as wavelet decomposition and the ensemble empirical mode decomposition methods as stressed by Niu et al. [73]. This mitigates the effects of error accumulation over time. To create the VMD decomposition, several parameters must be selected which are set with the trial and error procedure. By means of the VMD process, the IMF1 time-series was decomposed into eleven various components for IMF1. The decomposed time-series of the IMF1 dataset using the VMD approach is presented in Figure 5.

Finally, the predicted values community of these IMFs was applied to provide the estimated IMF1 value and the VMD-EEMD. Figure 6 presents a diagram of the developed ensemble decomposition-based proposed models. Furthermore, design parameters for both GEP and RFR models in calibration and validation periods were considered constant which are shown in

Table 4. Design parameters of gene expression programming (GEP) and random forest regression (RFR) models for calibration and validation stages at the three gauging stations.

Model	Design Parameters
GEP	Chromosomes	Gene size	HEAD SIZE	Linking Function	Mutation Rate	Crossover Rate	One and two point recombination rate	IS and RIS transposition rate
	40	3	8	Addition	0.01	0.8	0.3	0.1
RFR	Bag size percent	Leaf	Batch size	Surrogate	Delta Criterion	Number of depth	Seed	Out-of-Bag error
	200	8	100	True	0.1007	0	1	False

.

3.2. Application

3.2.1. The Siira Gauging Station

Results from standalone and hybrid models for forecasting daily streamflow at Siira are presented in

Table 5. Evaluation metrics of the proposed models in the calibration and validation periods at the Siira station.

Models	Statistical Error Indices
	GEP	RFR	EEMD-VMD-GEP	EEMD-VMD-RFR
Total Available Data in Calibration Stage
NSE	0.927	0.93	0.944	0.972
RMSE (m3/s)	3.731	3.482	3.26	2.3
MAE (m3/s)	1.313	1.358	1.301	1.056
RSD (m3/s)	0.269	0.251	0.235	0.166
U95	28.116	27.99	27.82	27.32
Reliability (%)	85.94	86.47	89.08	90.96
Resilience (%)	67.24	54.79	69.44	71.21
Total Available Data in Validation Stage
NSE	0.892	0.75	0.933	0.944
RMSE (m3/s)	2.286	3.491	1.806	1.645
MAE (m3/s)	0.906	1.282	0.722	0.683
RSD (m3/s)	0.327	0.499	0.258	0.235
U95	14.403	15.303	14.13	14.06
Reliability (%)	89.49	85.68	92.69	95.88
Resilience (%)	68.44	61.674	78.47	82.43

which the statistical metrics are applied for evaluation of the performance of GEP, RFR, EEMD-VMD-GEP, and EEMD-VMD-RFR models in calibration (1954–1994) and validation periods (1994–2008).

Performance assessment in Table 5 with respect to the statistical indices, NSE, RMSE, MAE, and RSD, indicated remarkable outcomes. In this station, the most accurate model in term of NSE was recorded from EEMD-VMD-RFR (NSE = 0.97) compared with GEP (0.92), RFR (0.93), and EEMD-VMD-GEP (0.94), while the largest error in term of RMSE, and RSD was calculated for GEP, 3.731 m³/s and 0.269 m³/s, respectively. In terms of MAE, the RFR revealed the least performance with 1.358, while EEMD-VMD-RFR has the best performance (MAE = 1.056 m³/s) for which the predicted values of streamflow is well-correlated with the calibration period.

To provide more detail in the results, three additional evaluation indices based on U95, reliability and resilience of models are considered to examine the proposed predictive models. To determine the model’s deviation in term of predicted daily streamflow, U95 is calculated and that 1.96 is a coverage factor corresponding to the 95% confidence level of predicted values of the models. Therefore, the hybrid EEMD-VMD-RFR model registers a lower value of U95, of approximately 27.32% during the calibration period, whereas the reliability (90.96%) and resilience (71.21%) values of this model showed relatively larger values compared with the other three approaches in the calibration period.

The modeling results during the validation period revealed that RFR model poorly predicted streamflow records over time. RMSE is approximately 1.84 (m³/s) lower when daily streamflow is predicted using EEMD-VMD-RFR compared to the standalone RFR, and approximately 0.641(m³/s) and 0.161(m³/s) lower compared with the GEP and EEMD-VMD-GEP model, respectively (see Table 3). The Nash-Sutcliffe coefficient for EEMD-VMD-RFR showed very good performance compared with original GEP and RFR and hybrid EEMD-VMD-GEP models. Moreover, the RFR model produced the highest values of RSD (0.499 (m³/s)), and U95 (15.303%) indicating poor performance of the model for the Siira streamflow prediction. Conversely, the integration of RFR with EEMD-VMD led to improving the simulation remarkably (e.g., Resilience = 82.43% and Reliability = 95.88%).

The uncertainty analysis was also undertaken in the validation period to evaluate the predictive ability of the models. As shown in

Table 6. Uncertainty analyses for streamflow prediction using predictive models at the Siira station.

Models	Mean Prediction Error	Width of Uncertainty Band	Median	95% Predictive Error Interval
Siira Station
GEP	0.236	±4.456	7.719	−4.22 to 4.69
RFR	0.189	±6.831	7.788	−6.64 to 7.02
EEMD-VMD-GEP	0.208	±3.511	7.695	−3.28 to 3.74
EEMD-VMD-RFR	0.172	±3.192	7.401	−2.95 to 3.42

, mean predictive error for EEMD-VMD-RFR (0.172) is lower compared with the rest of AI-based models, though all proposed models overestimated daily streamflow by presenting positive values for mean predictive error. Moreover, the uncertainty band for the RFR is larger than those of the available predictive approaches, which is ±6.831.

The degree of agreement between observed and predicted streamflow at calibration and validation periods was visually evaluated using scatterplots (Figure 7). Analysis suggested that EEMD-VMD to RFR combination made a stronger correlation between predicted and observed streamflow compared to other predictive models. Further, with a comparison between modeled and observed daily streamflow indicated that the standalone RFR model performed weaker than GEP in daily streamflow prediction and is not able to capture high and low flow values as well as the GEP model (see Figure 8). However, the two-layer decomposition-based approaches (especially EEMD-VMD-RFR) revealed a very good simulation performance and were most effective in high flow prediction during validation period.

3.2.2. The Bilghan Gauging Station

Similar to prior application, an integration of EEMD, VMD decomposition and RFR models outperformed the best prediction in terms of performance criteria. In the calibration period, the calculated RMSE for two-phase decomposition GEP and RFR is 3.73 (m³/s) and 1.768 (m³/s), respectively (see

Table 7. Evaluation metrics of the proposed models in the calibration and validation periods at the Bilghan station.

Models	Statistical Error Indices
	GEP	RFR	EEMD-VMD-GEP	EEMD-VMD-RFR
Total Available Data in Calibration Stage
NSE	0.915	0.932	0.94	0.98
RMSE (m3/s)	4.55	4.063	3.73	1.768
MAE (m3/s)	1.655	1.508	2.11	0.747
RSD (m3/s)	0.291	0.261	0.24	0.11
U95	31.84	31.61	31.46	30.79
Reliability (%)	88.36	90.27	93.52	96.49
Resilience (%)	59.66	64.93	71.67	79.15
Total Available Data in Validation Period
NSE	0.85	0.87	0.90	0.92
RMSE (m3/s)	2.704	2.61	2.358	2.061
MAE (m3/s)	1.442	1.29	1.08	1.02
RSD (m3/s)	0.357	0.33	0.311	0.272
U95	15.75	15.83	15.24	14.66
Reliability (%)	88.507	93.89	95.64	96.82
Resilience (%)	55.39	81.97	82.02	86.85

). This reveals the proposed approach is excellent for daily streamflow simulation across the mountainous region. Results of standalone GEP and RFR results showed poor performances compared with hybrid decomposition based models in terms of RMSE. EEMD-VMD based GEP model ranked as the second-best AI model for daily streamflow prediction at the Bilghan station.

According to Table 7, this model has an acceptable prediction in term of accuracy (NSE = 0.90) and has a lower error values of RMSE, MAE, and RSD, with 2.358 (m³/s), 1.08 (m³/s), and 0.311 (m³/s), correspondingly, when compared with GEP (RMSE = 2.704 (m³/s), MAE = 1.442 (m³/s), and 0.357(m³/s)) and RFR (RMSE = 2.61 (m³/s), MAE = 1.29 (m³/s), and 0.33(m³/s)) in the validation stage. Moreover, by comparing the results of models, the reliability and resilience of EEMD-VMD-RFR show an increase by approximately 10% and 21% in comparison with RFR, where these criteria are around 92% and 78% for EEMD-VMD coupled with GEP in the validation period. Although, the uncertainty analysis resulted that all four AI models overpredicted daily streamflow (i.e., mean prediction error for all models is positive), it is interesting to note that EEMD-VMD-RFR produced a smaller range of the uncertainty bands with ±3.922 compared with GEP (±5.058), RFR (±5.514), and EEMD-VMD-GEP (±4.563) (

Table 8. Uncertainty analyses for streamflow prediction using predictive models at Bilghan station.

Models	Mean Prediction Error	Width of Uncertainty Band	Median	95% Predictive Error Interval
Bilghan Station
GEP	1.102	±5.058	16.52	−4.25 to 5.86
RFR	0.811	±5.514	15.684	−5.53 to 5.49
EEMD-VMD-GEP	0.483	±4.563	15.804	−4.18 to 4.94
EEMD-VMD-RFR	0.301	±3.922	15.78	−3.62 to 4.22

). In addition, the lowest 95% predictive error interval is calculated for the EEMD-VMD-RFR.

It is evident from the scatterplots (see Figure 9) that the EEMD-VMD-RFR model’s line of linear agreement between forecasted (y) and observed (x) daily streamflow in validation stage is closer to the ideal line (1:1) compared with the GEP, RFR, and EEMD-VMD-GEP models. It is clear that the EEMD-VMD-RFR model can provide an accurate value for streamflow at Bilghan compared with the other three forecasting models.

Figure 10 illustrates the predicted hydrographs using the four proposed models. As illustrated, the EEMD-VMD-FRF showed a much better agreement between predicted and observed times series which demonstrates the suitability of EEMD and VMD in pre-processing inputs/output data and predicting daily flow.

3.2.3. The Gachsar Gauging Station

Concurrent with prior stations (Siira and Bilghan stations), EEMD-VMD based GEP and RFR models outperformed in the calibration phase. The values of NSE, RMSE, MAE, RSD, U95, reliability, and resilience for each model at the Gachsar gauging station are presented in Table 6. Compare with the original GEP and RFR models in which no pre-processing procedure of model inputs/output were carried out, the accuracy (NSE = 0.98) of the EEMD-VMD-RFR is far better than RFR (NSE = 0.93) particularly in the calibration period. The EEMD-VMD approach, in addition, improved GEP accuracy by about 7%, whereas standalone GEP generated an NSE value of 0.89. The results in the validation stage show that EEMD-VMD-GEP had a lower percentage error for streamflow prediction in terms of RSD (37.43%) and U95 (3.60%) than standalone GEP model (RSD = 0.366 and U95 = 8.38). Regarding the two-phase decomposition approach (EEMD-VMD), the outcomes present that the RFR model yielded reliability of 97.56% and resilience of 88.29% for daily streamflow prediction, while these values are 96.27% and 92.15% for the GEP, indicating much better performance of an evolutionary algorithm (

Table 9. Evaluation metrics of the proposed models in the calibration and validation periods at the Gachsar station.

Models	Statistical Error Indices
	GEP	RFR	EEMD-VMD-GEP	EEMD-VMD-RFR
Total available data in calibration stage
NSE	0.89	0.934	0.95	0.98
RMSE (m3/s)	1.879	0.964	0.84	0.53
MAE (m3/s)	0.519	0.256	0.237	0.137
RSD (m3/s)	0.497	0.255	0.222	0.141
U95	5.274	7.64	7.59	7.482
Reliability (%)	91.52	93.98	94.06	96.16
Resilience (%)	54.49	78.65	77.18	85.33
Total available data in validation period
NSE	0.865	0.93	0.95	0.97
RMSE (m3/s)	1.47	1.013	0.62	0.516
MAE(m3/s)	0.647	0.357	0.302	0.29
RSD (m3/s)	0.366	0.252	0.229	0.178
U95	8.38	8.12	8.078	7.95
Reliability (%)	86.7	95.91	96.27	97.56
Resilience (%)	69.97	84.82	92.15	88.29

).

Table 10. Uncertainty analyses for streamflow prediction using predictive models at Gachsar station.

Models	Mean Prediction Error	Width of Uncertainty Band	Median	95% predictive Error Interval
Gachsar station
GEP	0.103	±2.876	4.11	−2.97 to 2.77
RFR	0.084	±1.986	4.236	−1.99 to 1.98
EEMD-VMD-GEP	0.021	±1.808	4.186	−1.78 to 1.83
EEMD-VMD-RFR	0.006	±1.402	4.15	−1.54 to 1.66

summarizes the outcomes of the uncertainty analysis. Analysis revealed that 95% predictive error interval for ensemble GEP ranges from −1.78 to +1.83 and for RFR varies from −1.54 to +1.66 are likely similar, while the mean predictive error for EEMD-RFR (0.006) is far lower than the EEMD-VMD-GEP (0.021). Moreover, the uncertainty bands for all four models vary significantly, in which the band for EEMD-VMD-RFR (±1.402) is closer than EEMD-VMD-GEP (±1.808), standalone GEP (±2.876) and RFR (±1.986).

Figure 11 represents the scatter plots of predicted and observed streamflows for the Gachsar station. Although RFR prediction is mostly underestimated, pre-processing technique remarkably improved the performance criteria throughout the simulation period. It is clearly observed that EEMD-VMD process highly influenced the model performances and the slopes of the EEMD-VMD-GEP and EEMD-VMD-RFR are very close to the perfect line compared to the GEP and RFR models. Additionally, the correlations between observed and predicted streamflow values for EEMD-VMD-RFR (for calibration R² = 0.98 and validation R² = 0.96) are higher than the EEMD-VMD-GEP (for calibration R² = 0.95 and validation R² = 0.94) technique.

Furthermore, calibration and validation results (Figure 12) indicate that predicted streamflow using EEMD-VMD technique is in well agreement with observational data. However, over- and underestimations of the time series values, particularly for the GEP simulation, can be visually observed from the time variation graphs. To this end, the two hybrid ensemble models provided skillful simulation in terms of predicting high and low flow variability.

3.2.4. Further Comparison Among Proposed Models

To visually evaluate the performance of models in the validation period, box plot and empirical cumulative distribution (ECDF) are illustrated in Figure 13 and Figure 14. Box plots indicated the spread of predicted and observed streamflow based on the quartiles, that the whiskers showed the variability outside of the 25th and 75th percentiles.

Moving from Siira, to Bilghan, and Gachsar stations, more dispersion and skewness is noted in the Gachsar prediction. Further, the prediction of EEMD-VMD-RFP is more skillful for Siira and Bilghan rather than the Gachsar station. In all cases, the GEP standalone prediction seems to poorly predict daily streamflow records underestimating the majority of high flow events.

Further, the percentage of the absolute forecasted error statistics value (|FE|) through the empirical cumulative distribution function (ECDF) were computed and analyzed for at three stations (see Figure 14). Regarding the percentage of errors illustrated in the minimum error bracket (i.e., from −5 to ±5 m³/s), the ECDF indicated the superiority of EEMD-VMD-RFR and EEMD-VMD-GEP models in predicting streamflow fluctuations. According to this error bracket, the EEMD-VMD-RFR performed slightly better than the rest of the models.

There are various limitations should be addressed to illustrate future avenues for further research, despite the outstanding accuracy of the ensemble decomposition-based GEP and RFR models for daily streamflow forecasting. It is a need to design an expert system for a real-time short-term forecasting tool that a technique should be performed at much shorter-term periods, such as hourly step-ahead flow forecasting. This requires adequate and accurate time-series data that was not available for the present study. One of the drawbacks of the EEMD-VMD-MARS/RFR is that its implementation is that it is time-consuming because it produces several numbers of IMFs. In this respect, this study suggests applying other techniques or modifying the proposed methods to speed up the simulation process.

4. Conclusions

This paper examined the performance of a hybrid ensemble decomposition method embedded with the EEMD combined with the VMD as a preprocessing approach. Two kinds of AI methods namely RFR and GEP were implemented for predicting daily streamflow across three different gauging stations, Siira, Bilghan, and Gachsar, at a mountainous area in Karaj basin, Iran

Compare to the results of standalone (GEP and RFR) and ensemble-based (EEMD-VMD-GEP/RFR) AI models, it is apparent that of the performance of all four developed algorithms are relatively high. Among all models, EEMD-VMD approach showed promising results in term of predicting high and low values of daily streamflow. The predictive errors and uncertainties associated with the developed EEMD-VMD- RFR model were smaller than those associated with other forecast models. The analysis suggested that data pre-processing approaches (e.g., EEMD and VMD) are key approaches in accurate prediction of daily streamflow dynamics over time. This result is vital for reliable management of study region where the available dataset may involve noises and higher order trends.

Overall, the EEMD-VMD-RFR algorithm outperformed the other models. The results obtained by the best performing model are satisfactory as evidence by highest NSE and lowest RMSE values. This reflects that a hybrid-based AI approach is a robust and useful tool for simulating daily streamflow over the mountainous region. However, most of the models could not successfully predict the extreme (high and low) flow events. The reason is the developed models are not predominantly trained on extreme events. This can be overcome in the future by the flexibility to incorporate auxiliary information and soft data, such as expert knowledge, into the algorithmic framework, which could provide more flexibility in simulation and assist water managers and dam operators. In summary, this research presents a novel study of testing various AI-based algorithms for streamflow prediction and gives a comprehensive comparison among popular AI methods in hydrologic simulation. The authors believe this unique feature of the AI methods, especially the EEMD-VMD-RFR algorithm, is to be able to be further employed in the study region and provide more flexibility by adding desired decision variables for reservoir management. However, the proposed methodologies in this study are universally applicable to other mountainous regions, and are flexible to incorporate and test for other hydrologic time series data, such as flood records.