Water Balance for a Tropical Lake in the Volcanic Highlands: Lake Tana, Ethiopia
Abstract
:1. Introduction
2. Lake Tana and Its Basin
3. Data and Methods
3.1. Available Long-Term Hydrological, Meteorological, and Lake-Level Data
3.1.1. Precipitation
3.1.2. River Discharge Data
3.1.3. Lake Levels
3.1.4. Outflow by the Blue Nile River
3.1.5. Storage Characteristics of Lake Tana
3.2. Methods and Calculations
3.2.1. Lake Water Balance
3.2.2. Precipitation
3.2.3. Evaporation
3.2.4. Groundwater Inflow and Outflow
3.2.5. Lake Inflow from Rivers and Unaccounted Losses
3.3. Performance Evaluation
4. Results
4.1. Rainfall on the Lake Surface
4.2. Lake Evaporation
4.3. Lake Level
4.4. Lake Outflow
4.5. Inflow to the Lake and Unaccounted Water Losses
4.6. Regionalization and Unaccounted Loss of Water
4.6.1. Regionalization Factor
4.6.2. Gauged and Ungauged Runoff
4.6.3. Water Loss in the Lake
4.7. Lake Level
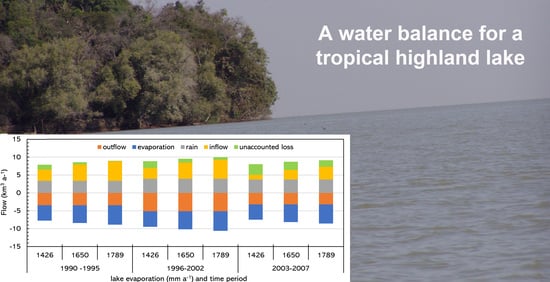
4.8. Lake Water Balance
5. Discussion
5.1. Optimal Rainfall and Evaporation Rates
5.2. Inflow from Gauged and Ungauged Watersheds of Lake Tana
5.3. Unaccounted Losses of Lake Water
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Units | 1990–1995 | 1996–2002 | 2003–2007 | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Evaporation | mm a−1 | 1426 | 1650 | 1789 | 1480 | 1650 | 1789 | 1426 | 1650 | 1789 | |
| land based | evaporation | km3 a−1 | −4.31 | −4.98 | −5.40 | −4.35 | −5.04 | −5.46 | −4.27 | −4.94 | −5.35 |
| outflow | km3 a−1 | −3.44 | −3.44 | 3.44 | −5.12 | −5.12 | −5.12 | −3.22 | −3.22 | −3.22 | |
| rain | km3 a−1 | 3.40 | 3.40 | 3.40 | 3.95 | 3.95 | 3.95 | 3.75 | 3.75 | 3.75 | |
| Inflow + loss | km3 a−1 | 4.49 | 5.17 | 5.59 | 5.21 | 5.89 | 6.32 | 4.28 | 4.95 | 5.37 | |
| inflow | km3 a−1 | 3.17 | 4.57 | 5.47 | 3.29 | 4.81 | 5.60 | 1.28 | 2.67 | 3.57 | |
| unaccounted loss | km3 a−1 | 1.32 | 0.60 | 0.12 | 1.92 | 1.08 | 0.72 | 3.00 | 2.28 | 1.80 | |
| lake level change | km3 a−1 | 0.14 | 0.14 | 0.14 | −0.31 | −0.31 | −0.31 | 0.55 | 0.55 | 0.55 | |
| Lake + land based | evaporation | km3 a−1 | −4.31 | −4.98 | −5.40 | −4.35 | −5.04 | −5.46 | −4.27 | −4.94 | −5.35 |
| outflow | km3 a−1 | −3.44 | −3.44 | −3.44 | −5.12 | −5.12 | −5.12 | −3.22 | −3.22 | −3.22 | |
| rain | km3 a−1 | 3.64 | 3.64 | 3.64 | 4.23 | 4.23 | 4.23 | 3.89 | 3.89 | 3.89 | |
| Inflow +loss | km3 a−1 | 4.25 | 4.93 | 5.35 | 4.93 | 5.61 | 6.04 | 4.14 | 4.81 | 5.23 | |
| inflow | km3 a−1 | 2.81 | 4.33 | 5.11 | 3.01 | 4.41 | 5.32 | 1.14 | 2.53 | 3.43 | |
| unaccounted loss | km3 a−1 | 1.44 | 0.60 | 0.24 | 1.92 | 1.20 | 0.72 | 3.00 | 2.28 | 1.80 | |
| lake level change | km3 a−1 | 0.14 | 0.14 | 0.14 | −0.31 | −0.31 | −0.31 | 0.55 | 0.55 | 0.55 | |
References
- Rodionov, S.N. Caspian Sea Level and Anticipated Global Warming. In Global and Regional Climate Interaction: The Caspian Sea Experience; Springer: Berlin/Heidelberg, Germany, 1994; pp. 154–195. [Google Scholar]
- Coe, M.T.; Foley, J.A. Human and natural impacts on the water resources of the Lake Chad basin. J. Geophys. Res. Atmos. 2001, 106, 3349–3356. [Google Scholar] [CrossRef]
- Micklin, P. The Aral sea disaster. Annu. Rev. Earth Planet. Sci. 2007, 35, 47–72. [Google Scholar] [CrossRef] [Green Version]
- Tsegaye, K. Action, inaction and environmental destruction: Socionatural determinants of the disappearance of Lake Alemaya (Haromaya), eastern Ethiopia. East. Ethiop. 2014, 3, 361–369. [Google Scholar] [CrossRef]
- Nicholson, S.E. Historical fluctuations of Lake Victoria and other lakes in the northern Rift Valley of East Africa. In Environmental Change and Response in East African Lakes; Springer: Berlin/Heidelberg, Germany, 1998; pp. 7–35. [Google Scholar]
- Steenhuis, T.S.; Hrnčíř, M.; Poteau, D.; Luna, E.J.R.; Tilahun, S.A.; Caballero, L.A.; Guzman, C.D.; Stoof, C.R.; Šanda, M.; Yitaferu, B. A saturated excess runoff pedo transfer function for vegetated watersheds. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Kebede, S.; Travi, Y.; Alemayehu, T.; Marc, V. Water balance of Lake Tana and its sensitivity to fluctuations in rainfall, Blue Nile basin, Ethiopia. J. Hydrol. 2006, 316, 233–247. [Google Scholar] [CrossRef]
- SMEC I. Hydrological study of the Tana-Beles sub-basins. In Surface Water Investigation; MOWR: Addis Ababa, Ethiopia, 2008. [Google Scholar]
- Alemayehu, T.; McCartney, M.; Kebede, S. Simulation of water resource development and environmental flows in the Lake Tana subbasin. In Improved Water and Land Management in the Ethiopian Highlands: Its Impact on Downstream Stakeholders Dependent on the Blue Nile, Proceedings of the Intermediate Results Dissimination Workshop held at the International Livestock Research Center (ILRI), Addis Ababa, Ethiopia, 5–6 February 2009; International Water Management Institure: Colombia, Sri Lanka, 2009. [Google Scholar] [CrossRef]
- Worqlul, A.W.; Collick, A.S.; Rossiter, D.G.; Langan, S.; Steenhuis, T.S. Assessment of surface water irrigation potential in the Ethiopian highlands: The Lake Tana Basin. Catena 2015, 129, 76–85. [Google Scholar] [CrossRef]
- Burney, J.A.; Naylor, R.L.; Postel, S.L. The case for distributed irrigation as a development priority in sub-Saharan Africa. Proc. Natl. Acad. Sci. USA 2013, 110, 12513–12517. [Google Scholar] [CrossRef] [Green Version]
- Legesse, S.A. Environmental protection in the Lake Tana basin. In Social and Ecological System Dynamics; Springer: Berlin/Heidelberg, Germany, 2017; pp. 433–452. [Google Scholar]
- Dessie, M.; Verhoest, N.E.; Adgo, E.; Poesen, J.; Nyssen, J. Scenario-based decision support for an integrated management of water resources. Int. J. River Basin Manag. 2017, 15, 485–502. [Google Scholar] [CrossRef]
- Alemu, M.L.; Geset, M.; Mosa, H.M.; Zemale, F.A.; Moges, M.A.; Giri, S.K.; Tillahun, S.A.; Melesse, A.M.; Ayana, E.K.; Steenhuis, T.S. Spatial and temporal trends of recent dissolved phosphorus concentrations in Lake Tana and its four main tributaries. Land Degrad. Dev. 2017, 28, 1742–1751. [Google Scholar] [CrossRef]
- Abera, B.; KIbret, M.; Van Echelpoel, W.; Kahsay, A.; Zelalem, W.; Ayalew, D.; Adgo, E.; Nyssen, J.; Goethals, P.; Verleyen, E. Physical and chemical limnology of Lake Tana and its tributary rivers. In Institutional University Cooperation with Bahir Dar University-Year 3 Joint Steering Committee Meeting-Excursion Guide; Bahir Dar University; Bahir Dar Ethiopia, & VLIR-UOS: Brussels, Ethiopia, 2019; pp. 10–12. [Google Scholar]
- Grabham, G.W. Report of the Mission to Lake Tana 1920–1921; Government Press: Cairo, Egypts, 1925. [Google Scholar]
- Cheesman, R.E. Lake Tana and the Blue Nile: An Abyssinian Quest; Macmillan and Co.: London, UK, 1936. [Google Scholar]
- Hurst, H.; Philips, P. The Nile Basin. In Ten-Day Mean and Monthly Mean Discharges of the Nile and Its Tributaries; Ministry of Public Works, Physical Department: Cairo, Egypt, 1933; Volume IV. [Google Scholar]
- Conway, D. The climate and hydrology of the Upper Blue Nile River. Geogr. J. 2000, 166, 49–62. [Google Scholar] [CrossRef] [Green Version]
- Sutcliffe, J.V.; Parks, Y.P. The Hydrology of the Nile; IAHS Press: Wallingford, UK, 1999. [Google Scholar]
- Aragie, M.A. Reservoir Operation and Establishment of Reservoir Rule for Lake Tana. Master’s Thesis, Faculty of Technology, Addis Ababa University, Addis Ababa, Ethiopia, 2005. [Google Scholar]
- Pelgrum, H.; Bastiaanssen, W. Remote Sensing Studies of the Tana-Bales Sub Basins; Water Watch Remote Sensing Services. University of Twente Faculty of Geo-Information and Earth Observation (ITC): Enschede, The Netherlands, 2006. [Google Scholar]
- Gieske, A.; Rientjes, T.; Haile, A.T.; Worqlul, A.W.; Asmerom, G.H. Determination of Lake Tana evaporation by the combined use of SEVIRI, AVHRR and IASI. In Proceedings of the 2008 EUMETSAT Meteorological Satellite Conference, Darmstadt, Germany, 8–12 September 2008. [Google Scholar]
- Wale, A.; Rientjes, T.; Gieske, A.; Getachew, H. Ungauged catchment contributions to Lake Tana’s water balance. Hydrol. Process. Int. J. 2009, 23, 3682–3693. [Google Scholar] [CrossRef]
- Chebud, Y.A.; Melesse, A.M. Modelling lake stage and water balance of Lake Tana, Ethiopia. Hydrol. Process. Int. J. 2009, 23, 3534–3544. [Google Scholar] [CrossRef]
- Setegn, S.G.; Srinivasan, R.; Dargahi, B. Hydrological modelling in the Lake Tana Basin, Ethiopia using SWAT model. Open Hydrol. J. 2008, 2, 49–62. [Google Scholar] [CrossRef] [Green Version]
- Rientjes, T.; Perera, B.; Haile, A.; Reggiani, P.; Muthuwatta, L. Regionalisation for lake level simulation-the case of Lake Tana in the Upper Blue Nile, Ethiopia. Hydrol. Earth Syst. Sci. 2011, 15, 1167. [Google Scholar] [CrossRef]
- Tegegne, G.; Hailu, D.; Aranganathan, S.M. Lake Tana reservoir water balance model. Int. J. Appl. Innov. Eng. Manag. 2013, 2, 474–478. [Google Scholar]
- Nigatu, Z.M. Hydrological Impacts of Climate Change on Lake Tana’s Water Balance; University of Twente Faculty of Geo-Information and Earth Observation (ITC): Enschede, The Netherlands, 2013. [Google Scholar]
- Duan, Z.; Gao, H.; Ke, C. Estimation of lake outflow from the poorly gauged Lake Tana (Ethiopia) using satellite remote sensing data. Remote Sens. 2018, 10, 1060. [Google Scholar] [CrossRef] [Green Version]
- Dessie, M.; Verhoest, N.E.; Pauwels, V.R.; Adgo, E.; Deckers, J.; Poesen, J.; Nyssen, J. Water balance of a lake with floodplain buffering: Lake Tana, Blue Nile Basin, Ethiopia. J. Hydrol. 2015, 522, 174–186. [Google Scholar] [CrossRef]
- Kebede, S.; Admasu, G.; Travi, Y. Estimating ungauged catchment flows from Lake Tana floodplains, Ethiopia: An isotope hydrological approach. Isot. Environ. Health Stud. 2011, 47, 71–86. [Google Scholar] [CrossRef]
- Mamo, S.; Ayenew, T.; Berehanu, B.; Kebede, S. Hydrology of the Lake Tana Basin, Ethiopia: Implication to Groundwater-Surface Waters Interaction. J. Environ. Earth Sci. 2016, 6, 54–66. [Google Scholar]
- Segond, M.-L.; Wheater, H.S.; Onof, C. The significance of spatial rainfall representation for flood runoff estimation: A numerical evaluation based on the Lee catchment, UK. J. Hydrol. 2007, 347, 116–131. [Google Scholar] [CrossRef]
- Kizza, M.; Westerberg, I.; Rodhe, A.; Ntale, H.K. Estimating areal rainfall over Lake Victoria and its basin using ground-based and satellite data. J. Hydrol. 2012, 464, 401–411. [Google Scholar] [CrossRef]
- Ba, M.B.; Nicholson, S.E. Analysis of convective activity and its relationship to the rainfall over the Rift Valley lakes of East Africa during 1983–90 using the Meteosat infrared channel. J. Appl. Meteorol. 1998, 37, 1250–1264. [Google Scholar] [CrossRef]
- Cheung, W.H.; Senay, G.B.; Singh, A. Trends and spatial distribution of annual and seasonal rainfall in Ethiopia. Int. J. Climatol. J. R. Meteorol. Soc. 2008, 28, 1723–1734. [Google Scholar] [CrossRef]
- Belete, M.A. Modeling and Analysis of Lake Tana Sub Basin Water Resources Systems, Ethiopia. Ph.D. Thesis, Faculty of Agricultural and Environmental Sciences, Rostock University, Rockstock, Germany, 2014. [Google Scholar]
- Chanie, T.; Collick, A.S.; Adgo, E.; Lehmann, C.J.; Steenhuis, T.S. Eco-hydrological impacts of Eucalyptus in the semi humid Ethiopian Highlands: The Lake Tana Plain. J. Hydrol. Hydromech. 2013, 61, 21–29. [Google Scholar] [CrossRef] [Green Version]
- Dagnew, D.C.; Guzman, C.D.; Zegeye, A.D.; Tibebu, T.Y.; Getaneh, M.; Abate, S.; Zemale, F.A.; Ayana, E.K.; Tilahun, S.A.; Steenhuis, T.S. Impact of conservation practices on runoff and soil loss in the sub-humid Ethiopian Highlands: The Debre Mawi watershed. J. Hydrol. Hydromech. 2015, 63, 210–219. [Google Scholar] [CrossRef] [Green Version]
- Mhiret, D.A.; Dagnew, D.C.; Alemie, T.C.; Guzman, C.D.; Tilahun, S.A.; Zaitchik, B.F.; Steenhuis, T.S. Impact of Soil Conservation and Eucalyptus on Hydrology and Soil Loss in the Ethiopian Highlands. Water 2019, 11, 2299. [Google Scholar] [CrossRef] [Green Version]
- Enku, T.; Melesse, A.M.; Ayana, E.K.; Tilahun, S.A.; Abate, M.; Steenhuis, T.S. Groundwater use of a small Eucalyptus patch during the dry monsoon phase. Biologia 2020, 75, 853–864. [Google Scholar] [CrossRef]
- Enku, T.; Melesse, A.M.; Ayana, E.K.; Tilahun, S.A.; Abate, M.; Steenhuis, T.S. Groundwater evaporation and recharge for a floodplain in a sub-humid monsoon climate in Ethiopia. Land Degrad. Dev. 2017, 28, 1831–1841. [Google Scholar] [CrossRef]
- Zimale, F.A.; Moges, M.A.; Alemu, M.L.; Ayana, E.K.; Demissie, S.S.; Tilahun, S.A.; Steenhuis, T.S. Budgeting suspended sediment fluxes in tropical monsoonal watersheds with limited data: The Lake Tana basin. J. Hydrol. Hydromech. 2018, 66, 65–78. [Google Scholar] [CrossRef] [Green Version]
- Fenta, A.A.; Yasuda, H.; Shimizu, K.; Ibaraki, Y.; Haregeweyn, N.; Kawai, T.; Belay, A.S.; Sultan, D.; Ebabu, K. Evaluation of satellite rainfall estimates over the Lake Tana basin at the source region of the Blue Nile River. Atmos. Res. 2018, 212, 43–53. [Google Scholar] [CrossRef]
- Appelhans, T.; Nauss, T. Spatial patterns of sea surface temperature influences on East African precipitation as revealed by empirical orthogonal teleconnections. Front. Earth Sci. 2016, 4, 3. [Google Scholar] [CrossRef] [Green Version]
- Goshime, D.W.; Absi, R.; Ledésert, B. Evaluation and bias correction of CHIRP rainfall estimate for rainfall-runoff simulation over Lake Ziway watershed, Ethiopia. Hydrology 2019, 6, 68. [Google Scholar] [CrossRef] [Green Version]
- Crétaux, J.-F.; Jelinski, W.; Calmant, S.; Kouraev, A.; Vuglinski, V.; Bergé-Nguyen, M.; Gennero, M.-C.; Nino, F.; Del Rio, R.A.; Cazenave, A. SOLS: A lake database to monitor in the Near Real Time water level and storage variations from remote sensing data. Adv. Space Res. 2011, 47, 1497–1507. [Google Scholar] [CrossRef]
- Kebedew, M.G.; Kibret, A.A.; Tilahun, S.A.; Belete, M.A.; Zimale, F.A.; Steenhuis, T.S. The Relationship of Lake Morphometry and Phosphorus Dynamics of a Tropical Highland Lake: Lake Tana, Ethiopia. Water 2020, 12, 2243. [Google Scholar] [CrossRef]
- Ayana, E.K. Validation of Radar Altimetry Lake Level Data and It’s Application in Water Resource Management. Master’s Thesis, University of Twente, Enschede, The Netherlands, 2007. [Google Scholar]
- Worqlul, A.W.; Ayana, E.K.; Maathuis, B.H.; MacAlister, C.; Philpot, W.D.; Leyton, J.M.O.; Steenhuis, T.S. Performance of bias corrected MPEG rainfall estimate for rainfall-runoff simulation in the upper Blue Nile Basin, Ethiopia. J. Hydrol. 2018, 556, 1182–1191. [Google Scholar] [CrossRef]
- Adem, A.A.; Aynalem, D.W.; Tilahun, S.A.; Steenhuis, T.S. Predicting reference evaporation for the Ethiopian highlands. J. Water Resour. Prot. 2017, 9, 1244. [Google Scholar] [CrossRef] [Green Version]
- Allen, R.G.; Pereira, L.S.; Raes, D.; Smith, M. Crop Evapotranspiration-Guidelines for Computing Crop Water Requirements-FAO Irrigation and Drainage Paper 56; FAO: Rome, Italy, 1998. [Google Scholar]
- Zimale, F.A. Estimation of Water Balance Components Using Remote Sensing Products in the Upper Blue Nile, Lake Tana Sub Basin. Master’s Thesis, Arba Minch University, Arba Minch, Ethiopia, 2009. [Google Scholar]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models part I—A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Burt, J.E.; Barber, G.M.; Rigby, D.L. Elementary Statistics for Geographers; Guilford Press: New York, NY, USA, 2009. [Google Scholar]
- Worqlul, A.; Collick, A.; Tilahun, S.; Langan, S.; Rientjes, T.; Steenhuis, T. Comparing TRMM 3B42, CFSR and ground-based rainfall estimates as input for hydrological models, in data scarce regions: The Upper Blue Nile Basin, Ethiopia. Hydrol. Earth Syst. Sci. Discuss. 2015, 12, 2081–2112. [Google Scholar] [CrossRef]
- Abate, M.; Nyssen, J.; Moges, M.M.; Enku, T.; Zimale, F.A.; Tilahun, S.A.; Adgo, E.; Steenhuis, T.S. Long-Term Landscape Changes in the Lake Tana Basin as Evidenced by Delta Development and Floodplain Aggradation in Ethiopia. Land Degrad. Dev. 2017, 28, 1820–1830. [Google Scholar] [CrossRef]
- Abate, M.; Nyssen, J.; Steenhuis, T.S.; Moges, M.M.; Tilahun, S.A.; Enku, T.; Adgo, E. Morphological changes of Gumara River channel over 50 years, upper Blue Nile basin, Ethiopia. J. Hydrol. 2015, 525, 152–164. [Google Scholar] [CrossRef]
- Zegeye, A.D.; Langendoen, E.J.; Guzman, C.D.; Dagnew, D.C.; Amare, S.D.; Tilahun, S.A.; Steenhuis, T.S. Gullies, a critical link in landscape soil loss: A case study in the subhumid highlands of Ethiopia. Land Degrad. Dev. 2018, 29, 1222–1232. [Google Scholar] [CrossRef]
- Zegeye, A.D.; Langendoen, E.J.; Stoof, C.R.; Tilahun, S.A.; Dagnew, D.C.; Zimale, F.A.; Guzman, C.D.; Yitaferu, B.; Steenhuis, T.S. Morphological dynamics of gully systems in the subhumid Ethiopian Highlands: The Debre Mawi watershed. Soil 2016, 2, 443–458. [Google Scholar] [CrossRef] [Green Version]
- Abebe, W.B.; Tilahun, S.A.; Moges, M.M.; Wondie, A.; Derseh, M.G.; Nigatu, T.A.; Mhiret, D.A.; Steenhuis, T.S.; Camp, M.V.; Walraevens, K. Hydrological foundation as a basis for a holistic environmental flow assessment of tropical highland rivers in ethiopia. Water 2020, 12, 547. [Google Scholar] [CrossRef] [Green Version]
- Nieber, J.L.; Sidle, R.C. How do disconnected macropores in sloping soils facilitate preferential flow? Hydrol. Process. 2010, 24, 1582–1594. [Google Scholar] [CrossRef]
- Wilson, G.V.; Nieber, J.L.; Sidle, R.C.; Fox, G.A. Internal erosion during soil pipeflow: State of the science for experimental and numerical analysis. Trans. ASABE 2013, 56, 465–478. [Google Scholar] [CrossRef]
- Adem, A.A.; Gashaw, A.; Aynalem, D.W.; Tilahun, S.A.; Mekuria, W.; Azeze, M.; Steenhuis, T.S. Hydrogeology of Volcanic Highlands Affect Prioritization of Land Management Practices. Water 2020, 12, 2702. [Google Scholar] [CrossRef]
- Adem, A.A.; Aynalem, D.W.; Tilahun, S.A.; Mekuria, W.; Azeze, M.; Steenhuis, T.S. Runoff response and the associated soil and nutrient loss in two northwestern Ethiopian highland watersheds. In Proceedings of the International Conference on the Advancement of Science and Technology (ICAST-CWRE-2017), Bahar Dar, Ethiopia, May 2017; pp. 30–35. [Google Scholar]
- Addisie, M.B.; Ayele, G.K.; Gessess, A.A.; Tilahun, S.A.; Zegeye, A.D.; Moges, M.M.; Schmitter, P.; Langendoen, E.J.; Steenhuis, T.S. Gully head retreat in the sub-humid Ethiopian Highlands: The Ene-Chilala catchment. Land Degrad. Dev. 2017, 28, 1579–1588. [Google Scholar] [CrossRef]
- Demlie, M.; Ayenew, T.; Wohnlich, S. Comprehensive hydrological and hydrogeological study of topographically closed lakes in highland Ethiopia: The case of Hayq and Ardibo. J. Hydrol. 2007, 339, 145–158. [Google Scholar] [CrossRef]
- Kebede, S.; Zewdu, S. Use of Rn-222 and delta O-18-delta H-2 isotopes in detecting the origin of water and in quantifying groundwater inflow rates in an alarmingly growing lake, ethiopia. Water 2019, 11, 2591. [Google Scholar] [CrossRef] [Green Version]
- Hirayama, Y.; Okawa, A.; Nakamachi, K.; Aoyama, T.; Okada, Y.; Oi, T.; Hirose, K.; Kikawada, Y. Estimation of water seepage rate in the active crater lake system of Kusatsu-Shirane volcano, Japan, using FDNPP-derived radioactive cesium as a hydrological trace. J. Environ. Radioact. 2020, 218, 106257. [Google Scholar] [CrossRef]
- Ozyavas, A.; Khan, S.D. The driving forces behind the Caspian Sea mean water level oscillations. Environ. Earth Sci. 2012, 65, 1821–1830. [Google Scholar] [CrossRef]
- Web of Science. Web of Science Core Collection Clarivate. Available online: https://clarivate.com/webofsciencegroup/solutions/webofscience-platform/ (accessed on 27 September 2020).
- Lamb, H.F.; Bates, C.R.; Bryant, C.L.; Davies, S.J.; Marshall, M.H.; Huws, D.G.; Roberts, H.M.; Toland, H. 150,000-year palaeoclimate record from northern Ethiopia supports early, multiple dispersals of modern humans from Africa. Sci. Rep. 2018, 8, 1077. [Google Scholar] [CrossRef] [PubMed] [Green Version]












| Study Period | Evaporation mm a−1 | Precipitation mm a−1 | Inflow mm a−1 | Outflow mm a−1 | Loss mm a−1 | Remarks | ||
|---|---|---|---|---|---|---|---|---|
| Start | End | |||||||
| Conway [19] | 1921 | 1931 | 1236 | |||||
| Sutcliffe et al. [20] | 1921 | 1933 | 1207 | |||||
| Kebede et al. [7] | 1960 | 1992 | 1478 | 1451 | 1162 | 1113 | 22 | |
| Aragie [20] | 1964 | 2000 | 2634 | 1224 | 2594 | 1184 | 0 | SCS CN |
| Pelgrum et al. [22] | 2001 | 1588 | 1541 | 1616 | 1499 | 70 | satellite | |
| SMEC [8] | 1960 | 1995 | 1650 | 1260 | 1622 | 1231 | 1 | fitted |
| Gieske et al. [23] | 1992 | 2003 | 1671 | 1255 | 1770 | 1348 | 19 | fitted |
| Wale et al. [24] | 1992 | 2003 | 1690 | 1220 | 2160 | 1520 | 170 | HBV |
| Chebud et al. [25] | 1960 | 2003 | 1428 | 1198 | 1458 | 1679 | −451 | |
| Setegn et al. [26] | 1978 | 2004 | 1248 | 1375 | 1312 | 1280 | 159 | SWAT |
| Rientjes et al. [27] | 1994 | 2003 | 1563 | 1347 | 1781 | 1480 | 85 | Satellite |
| Tegegne et al. [28] | 1996 | 2002 | 1618 | 1291 | 2119 | 1725 | 67 | SWAT |
| Nigatu [29] | 1994 | 2003 | 2041 | 1274 | 2186 | 1520 | −101 | baseline |
| Duan et al. [30] | 2006 | 1688 | 1652 | 2226 | 1566 | 191 | TRMM | |
| Dessie et al. [31], scenario 1 | 2012 | 2013 | 1789 | 1330 | 2349 | 1618 | 273 | observed |
| Dessie et al. [31], scenario 2 | 2012 | 2013 | 1789 | 1330 | 2201 | 1618 | 125 | adjusted |
| Kebede et al. [32] | n.a.* | 1600 | 1216 | 1715 | 1172 | 147 | Isotopes | |
| Mamo et al. [33] | 1995 | 2005 | 1544 | 1315 | 2829 | 1552 | 945 | Isotopes |
| No | Area (km2) | |||
|---|---|---|---|---|
| Gauged | Ungauged | Total | ||
| 1 | Gilgel Abay | 1656 | 2065 | 3721 |
| 2 | Gumara | 1283 | 485 | 1768 |
| 3 | Rib | 1303 | 711 | 2014 |
| 4 | Megech | 514 | 476 | 990 |
| 5 | Remaining watersheds | 3529 | 3529 | |
| 6 | Lake | 3060 | ||
| Total | 4756 | 7266 | 15,082 | |
| Data | Period | Source |
|---|---|---|
| Climate data | 1990–2014 | Eth. National Meteorological Agency |
| Lake rainfall | 2013 and 2014 | Observed by the first author |
| CHIRPS-v2 rainfall | 1990–2014 | Climate Hazards Group Infrared Precipitation Version two |
| Gauged streamflow | 1990–2014 | Eth. Ministry of Water Irrigation and Energy |
| Ungauged Simulated streamflow | 1994–2012 | Literature |
| Outflow from the Lake | 1990–2014 | Eth. Ministry of Water Irrigation and Energy |
| Lake Evaporation | 1960–2006 | Literature |
| Lake level | 1990–2014 | Eth. Ministry of Water Irrigation and Energy |
| Lake level | 1992–2020 | Hydroweb (website) |
| Land-Based | Lake + Land-Based | |||||||
|---|---|---|---|---|---|---|---|---|
| Evaporation (mm a−1) | 1426 | 1650 | 1789 | 1426 | 1650 | 1789 | ||
| 1990–1995 | reg. factor α | 0.50 | 0.50 | 0.49 | 0.48 | 0.47 | 0.46 | |
| water loss | km3 a−1 | 1.32 | 0.60 | 0.12 | 1.44 | 0.72 | 0.24 | |
| 1996–2002 | reg. factor α | 0.61 | 0.61 | 0.60 | 0.56 | 0.56 | 0.55 | |
| water loss | km3 a−1 | 1.92 | 1.08 | 0.72 | 1.92 | 1.20 | 0.72 | |
| 2003–2007 | reg. factor α | 0.71 | 0.70 | 0.69 | 0.69 | 0.69 | 0.68 | |
| water loss | km3 a−1 | 3.00 | 2.28 | 1.80 | 3.00 | 2.28 | 1.80 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alemu, M.L.; Worqlul, A.W.; Zimale, F.A.; Tilahun, S.A.; Steenhuis, T.S. Water Balance for a Tropical Lake in the Volcanic Highlands: Lake Tana, Ethiopia. Water 2020, 12, 2737. https://doi.org/10.3390/w12102737
Alemu ML, Worqlul AW, Zimale FA, Tilahun SA, Steenhuis TS. Water Balance for a Tropical Lake in the Volcanic Highlands: Lake Tana, Ethiopia. Water. 2020; 12(10):2737. https://doi.org/10.3390/w12102737
Chicago/Turabian StyleAlemu, Muluken L., Abeyou W. Worqlul, Fasikaw A. Zimale, Seifu A. Tilahun, and Tammo S. Steenhuis. 2020. "Water Balance for a Tropical Lake in the Volcanic Highlands: Lake Tana, Ethiopia" Water 12, no. 10: 2737. https://doi.org/10.3390/w12102737
APA StyleAlemu, M. L., Worqlul, A. W., Zimale, F. A., Tilahun, S. A., & Steenhuis, T. S. (2020). Water Balance for a Tropical Lake in the Volcanic Highlands: Lake Tana, Ethiopia. Water, 12(10), 2737. https://doi.org/10.3390/w12102737