A Comprehensive View of the ASM1 Dynamic Model: Study on a Practical Case
Abstract
:1. Introduction
2. Materials and Methods
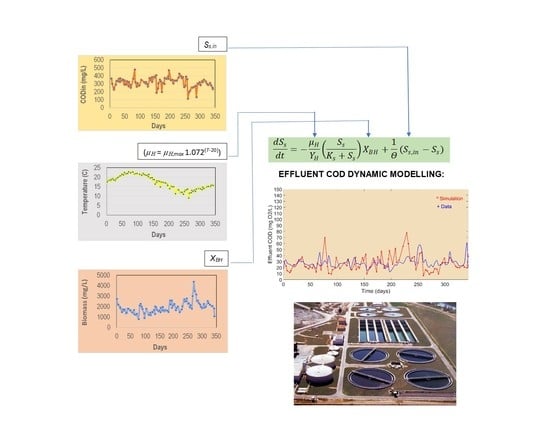
2.1. Dynamic Model ASM1
2.2. Uncoupling of the Components
2.3. Approximations in Process Rates
2.4. Experimental Setup
2.5. Biological Treatment in WWTP
2.6. Analytical Methods
3. Results and Discussion
3.1. Dynamic Variables
3.2. Tuning on YH
3.3. Tuning on μH,max
3.4. Fine Tuning on μH,max
4. Conclusions
Supplementary Materials
Funding
Institutional Review Board Statement
Informed Consent Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| Nomenclature | |
| bA | decay coefficient for autotrophic biomass (d−1); |
| bH | decay coefficient for heterotrophic biomass (d−1); |
| fp | fraction of biomass leading to particulate products; |
| iXB | nitrogen fraction in biomass; |
| iXP | nitrogen fraction in products from biomass; |
| k | kinetic coefficient (d−1); |
| kh | hydrolysis rate constant (d−1); |
| KOH | oxygen half-saturation coefficient for heterotrophic biomass (mg/L); |
| Ks | half-saturation coefficient for readily biodegradable substrate (mg/L); |
| KX | half-saturation coefficient for particulate biodegradable substrate (mg/L); |
| Q | influent flow rate (L/d); |
| ri | substrate utilization rate (mg/(L d)); |
| r(ξ) | conversion vector of the variable ξ (mg/(L d)); |
| SALK | alkalinity (mol/L); |
| SI | soluble inert organic matter (mg/L); |
| SND | soluble biodegradable organic nitrogen (mg/L); |
| SNH | ammonia nitrogen (mg/L); |
| SNO | nitrate and nitrite nitrogen (mg/L); |
| SO | dissolved oxygen (mg/L); |
| SS | readily biodegradable substrate (mg/L); |
| SS,in | influent readily biodegradable substrate (mg/L); |
| t | time (d); |
| T | temperature (°C); |
| V | reactor volume (L); |
| XBA | active autotrophic biomass (mg/L); |
| XBH | active heterotrophic biomass (mg/L); |
| XBH,in | influent active heterotrophic biomass (mg/L); |
| XI | particulate inert organic matter (mg/L); |
| XND | particulate biodegradable organic nitrogen (mg/L); |
| XP | particulate products arising from biomass decay (mg/L); |
| XS | slowly biodegradable substrate (mg/L); |
| XS,in | influent slowly biodegradable substrate (mg/L); |
| YA | growth yield of autotrophic biomass; |
| YH | growth yield of heterotrophic biomass. |
| Greek symbols | |
| ξ | vector of reactor and effluent concentration (mg/L); |
| ξin | vector of influent concentration (mg/L); |
| μH | specific growth rate for heterotrophic biomass (d−1); |
| μH,max | maximum specific growth rate for heterotrophic biomass (d−1); |
| ρ(ξ) | vector of reaction kinetics (mg/(L d)); |
| ρj | process rate (mg/(L d)); |
| Θ | hydraulic residence time, HRT (d); |
| νij | stoichiometric coefficient; |
| ηg | correction factor of μH under anoxic conditions; |
| ηh | correction factor for hydrolysis under anoxic conditions. |
References
- Henze, M.; Grady, C.P.L.; Gujer, W.; Marais, G.V.R.; Matsuo, T. A general model for single-sludge wastewater treatment systems. Water Res. 1987, 21, 505–515. [Google Scholar] [CrossRef] [Green Version]
- Gujer, W.; Henze, M.; Mino, T.; Matsuo, T.; Wentzel, M.C.; Marais, G.V.R. The activated sludge model no. 2: Biological phosphorus removal. Water Sci. Technol. 1995, 31, 1–11. [Google Scholar] [CrossRef]
- Gujer, W.; Henze, M.; Mino, T.; van Loosdrecht, M. Activated sludge model no.3. Water Sci. Technol. 1999, 39, 183–193. [Google Scholar] [CrossRef]
- Henze, M.; Gujer, W.; Mino, T.; Matsuo, T.; Wentzel, M.C.; Marais, G.V.R.; van Loosdrecht, M. Activated sludge model no. 2d. ASM2D. Water Sci. Technol. 1999, 39, 165–182. [Google Scholar] [CrossRef]
- Henze, M.; Gujer, W.; Mino, T.; van Loosdrecht, M. Activated Sludge Models ASM1, ASM2, ASM2d and ASM3; IWA Scientific and Technical Report No. 9; IWA Publishing: London, UK, 2000. [Google Scholar]
- Gernaey, K.V.; van Loosdrecht, M.; Henze, M.; Lind, M.; Jorgensen, S.B. Activated sludge wastewater treatment plant modelling and simulation: State of the art. Environ. Model. Softw. 2004, 19, 763–783. [Google Scholar] [CrossRef]
- Iacopozzi, I.; Innocenti, V.; Marsili-Libelli, S.; Giusti, E. A modified activated sludge model no. 3 (ASM3) with two-step nitrification-denitrification. Environ. Model. Softw. 2007, 22, 847–861. [Google Scholar] [CrossRef]
- Brun, R.; Kühni, M.; Siegrist, H.; Gujer, W.; Reichert, P. Practical identifiability of ASM2d parameters-systematic selection and tuning of parameter subsets. Water Res. 2002, 36, 4113–4127. [Google Scholar] [CrossRef]
- Reijken, C.; Giorgi, S.; Hurkmans, C.; Pérez, J.; van Loosdrecht, M. Incorporating the influent cellulose fraction in activated sludge modelling. Water Res. 2018, 144, 104–111. [Google Scholar] [CrossRef]
- Hu, H.; Liao, K.; Xie, W.; Wang, J.; Wu, B.; Ren, H. Modeling the formation of microorganism-derived dissolved organic nitrogen (mDON) in the activated sludge system. Water Res. 2020, 174, 115604. [Google Scholar] [CrossRef]
- Wu, X.; Yang, Y.; Wu, G.; Mao, J.; Zhou, T. Simulation and optimization of a coking wastewater biological treatment process by activated sludge models (ASM). Waste Manag. 2016, 165, 235–242. [Google Scholar] [CrossRef]
- Zhao, J.; Huang, J.; Guan, M.; Zhao, Y.; Chen, G.; Tian, X. Mathematical simulating the process of aerobic granular sludge treating high carbon and nitrogen concentration wastewater. Chem. Eng. J. 2016, 306, 676–684. [Google Scholar] [CrossRef]
- Baeten, J.E.; van Loosdrecht, M.; Volcke, E.I.P. Modelling aerobic granular sludge reactors through apparent halfsaturation coefficients. Water Res. 2018, 146, 134–145. [Google Scholar] [CrossRef] [PubMed]
- Du, X.; Ma, Y.; Wei, X.; Jegatheesan, V. Optimal Parameter Estimation in Activated Sludge Process Based Wastewater Treatment Practice. Water 2020, 12, 2604. [Google Scholar] [CrossRef]
- Spérandio, M.; Espinosa, M.C. Modelling an aerobic submerged membrane bioreactor with ASM models on a large range of sludge retention time. Desalination 2008, 231, 82–90. [Google Scholar] [CrossRef]
- Fenu, A.; Guglielmi, G.; Jimenez, J.; Spérandio, M.; Saroj, D.; Lesjean, B.; Brepols, C.; Thoeye, C.; Nopens, I. Activated sludge model (ASM) based modelling of membrane bioreactor (MBR) processes: A critical review with special regard to MBR specificities. Water Res. 2010, 44, 4272–4294. [Google Scholar] [CrossRef]
- Wágner, D.S.; Valverde-Pérez, B.; Sæbø, M.; Bregua de la Sotilla, M.; van Wagenen, J.; Smets, B.F.; Plósz, B.G. Towards a consensus-based biokinetic model for green microalgae-The ASM-A. Water Res. 2016, 103, 485–499. [Google Scholar] [CrossRef] [Green Version]
- Santos, J.M.M.; Rieger, L.; Lanham, A.B.; Carvalheira, M.; Reis, M.A.M.; Oehmen, A. A novel metabolic-ASM model for full-scale biological nutrient removal systems. Water Res. 2020, 171, 115373. [Google Scholar] [CrossRef]
- Acevedo, V.; Kaiser, T.; Babist, R.; Fundneider, T.; Lackner, S. A multi-component model for granular activated carbon filters combining biofilm and adsorption kinetics. Water Res. 2021, 197, 117079. [Google Scholar] [CrossRef]
- Lahdhiri, A.; Lesage, G.; Hannachi, A.; Heran, M. Steady-State Methodology for Activated Sludge Model 1 (ASM1) State Variable Calculation in MBR. Water 2020, 12, 3220. [Google Scholar] [CrossRef]
- Orhon, D.; Yucel, A.B.; Insel, G.; Solmaz, B.; Mermutlu, R.; Sözen, S. Appraisal of Super-Fast Membrane Bioreactors by MASM—A New Activated Sludge Model for Membrane Filtration. Water 2021, 13, 1963. [Google Scholar] [CrossRef]
- Smets, I.Y.; Haegebaert, J.V.; Carrette, R.; van Impe, J.F. Linearization of the activated sludge model ASM1 for fast and reliable predictions. Water Res. 2003, 37, 1831–1851. [Google Scholar] [CrossRef]
- Sharifi, S.; Murthy, S.; Takács, I.; Massoudieh, A. Probabilistic parameter estimation of activated sludge processes using Markov Chain Monte Carlo. Water Res. 2014, 50, 254–266. [Google Scholar] [CrossRef] [PubMed]
- APHA; AWWA; WEF. Standard Methods for the Examination of Water and Wastewater, 23rd ed.; American Public Health Association: Washington, DC, USA, 2017. [Google Scholar]
- Meijer, S.C.F.; van Loosdrecht, M.; Heijnen, J.J. Modelling the start-up of a full-scale biological phosphorous and nitrogen removing WWTP. Water Res. 2002, 36, 4667–4682. [Google Scholar] [CrossRef]
- Plattes, M.; Henry, E.; Schosseler, P.M.; Weidenhaupt, A. Modelling and dynamic simulation of a moving bed bioreactor for the treatment of municipal wastewater. Biochem. Eng. J. 2006, 32, 61–68. [Google Scholar] [CrossRef]
- Spérandio, M.; Massé, A.; Espinosa, M.C.; Cabassud, C. Characterization of sludge structure and activity in submerged membrane bioreactor. Water Sci. Technol. 2005, 52, 401–408. [Google Scholar] [CrossRef]
- Wang, C.; Zeng, Y.; Lou, J.; Wu, P. Dynamic simulation of a WWTP operated at low dissolved oxygen condition by integrating activated sludge model and floc model. Biochem. Eng. J. 2007, 33, 217–227. [Google Scholar] [CrossRef]
- Costa, C.; Rodríguez, J.; Márquez, M.C. A simplified dynamic model for the activated sludge process with high strength wastewaters. Environ. Model. Assess. 2009, 14, 739–747. [Google Scholar] [CrossRef]
- Tamrat, M.; Costa, C.; Márquez, M.C. Biological treatment of leachate from solid wastes: Kinetic study and simulation. Biochem. Eng. J. 2012, 66, 46–51. [Google Scholar] [CrossRef]
- Costa, C.; Domínguez, J.; Autrán, B.; Márquez, M.C. Dynamic modeling of biological treatment of leachates from solid wastes. Environ. Model. Assess. 2018, 23, 165–173. [Google Scholar] [CrossRef]






| i—Component→ j—Process↓ | 1 SI | 2 SS | 3 XI | 4 XS | 5 XBH | 6 XBA | 7 XP | 8 SO | 9 SNO | 10 SNH | 11 SND | 12 XND | 13 SALK |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1-Aerobic growth of heterotrophs | 1 | −iXB | |||||||||||
| 2-Anoxic growth of heterotrophs | 1 | −iXB | |||||||||||
| 3-Aerobic growth of autotrophs | 1 | ||||||||||||
| 4-Decay of heterotrophs | 1 − fP | −1 | fP | −iXB − fPiXP | |||||||||
| 5- Decay of autotrophs | 1 − fP | −1 | fP | −iXB − fPiXP | |||||||||
| 6-Ammonification of soluble organic nitrogen | 1 | −1 | |||||||||||
| 7-Hydrolysis of entrapped organics | 1 | −1 | |||||||||||
| 8-Hydrolysis of entrapped organic nitrogen | 1 | −1 |
| Process Rate | Mathematical Expression |
|---|---|
| 1—Heterotrophs, aerobic growth | |
| 2—Heterotrophs, anaerobic growth | |
| 3—Autotrophs, aerobic growth | |
| 4—Heterotrophs, decay | |
| 5—Autotrophs, decay | |
| 6—Organic nitrogen, ammonification | |
| 7—Hydrolysis of particulate organic matter | |
| 8—Hydrolysis of particulate organic nitrogen |
| Day | CODin | COD | Temp | Biomass |
|---|---|---|---|---|
| (mg/L) | (mg/L) | (°C) | (mg/L) | |
| 1 | ---- | 23.7 | 17.6 | 2723 |
| 5 | 367 | 32.9 | 18.3 | 2160 |
| 7 | 302 | 27.3 | 18.5 | 2210 |
| 12 | 229 | 25.3 | 18.3 | 1967 |
| 14 | 250 | 24.1 | 18.9 | 1850 |
| 19 | 290 | 21.6 | 19.2 | 1477 |
| 21 | 338 | 21.0 | 18.7 | 1730 |
| 26 | 331 | 27.2 | 18.4 | 1623 |
| 29 | 365 | 34.1 | 19.0 | 1720 |
| 33 | 326 | 29.3 | 19.5 | 1367 |
| 35 | 369 | 31.1 | 19.8 | 1433 |
| 40 | 342 | 25.9 | 20.5 | 1790 |
| 42 | 354 | 25.6 | 20.8 | 1787 |
| 47 | 290 | 23.7 | 21.1 | 1610 |
| 49 | 342 | 23.9 | 21.6 | 1647 |
| 54 | 291 | 26.2 | 21.4 | 1470 |
| 56 | 331 | 23.7 | 22.5 | 1447 |
| 61 | 269 | 18.6 | 21.7 | 1677 |
| 63 | 324 | 24.3 | 21.8 | 1277 |
| 68 | 284 | 45.6 | 22.0 | 1210 |
| 70 | 251 | 22.4 | 22.8 | 1310 |
| 77 | 364 | 31.4 | 22.4 | 810 |
| 82 | 478 | 25.9 | 22.9 | 2103 |
| 84 | 321 | 40.6 | 22.8 | 2263 |
| 89 | 265 | 21.5 | 21.6 | 1993 |
| 91 | 308 | 21.5 | 21.8 | 1770 |
| 96 | 278 | 21.1 | 21.8 | 1357 |
| 98 | 280 | 19.3 | 22.1 | 917 |
| 105 | 350 | 26.7 | 21.6 | 1790 |
| 113 | 321 | 27.5 | 21.1 | 1227 |
| 118 | 303 | 29.9 | 22.1 | 1410 |
| 120 | 322 | 35.0 | 21.4 | 1177 |
| 125 | 296 | 17.8 | 21.1 | 1527 |
| 127 | 267 | 22.7 | 21.1 | 1480 |
| 132 | 373 | 37.0 | 21.0 | 1673 |
| 134 | 368 | 30.2 | 20.3 | 1300 |
| 135 | 347 | 26.7 | 21.5 | 2027 |
| 139 | 384 | 26.9 | 19.5 | 1945 |
| 141 | 326 | 25.0 | 19.7 | 1715 |
| 147 | 390 | 27.2 | 19.8 | 1560 |
| 149 | 382 | 28.3 | 18.8 | 1623 |
| 153 | 408 | 23.6 | 18.8 | 1485 |
| 155 | 189 | 15.4 | 16.5 | 1895 |
| 160 | 244 | 18.1 | 17.4 | 1650 |
| 162 | 306 | 20.2 | 18.1 | 1968 |
| 167 | 352 | 27.6 | 18.1 | 1553 |
| 169 | 332 | 33.2 | 17.8 | 1618 |
| 173 | 198 | 23.2 | 14.9 | 1675 |
| 175 | 311 | 25.8 | 17.5 | 1635 |
| 180 | 300 | 33.9 | 17.2 | 1608 |
| 182 | 372 | 25.9 | 17.4 | 1490 |
| 187 | 369 | 24.7 | 17.0 | 2590 |
| 189 | 361 | 17.7 | 17.0 | 2215 |
| 194 | 392 | 27.3 | 16.5 | 2590 |
| 195 | 365 | 24.1 | 16.1 | 1895 |
| 197 | 469 | 12.6 | 15.7 | 2105 |
| 203 | 347 | 18.6 | 14.0 | 2255 |
| 208 | 349 | 24.9 | 15.4 | 1665 |
| 210 | 306 | 23.5 | 14.9 | 1860 |
| 215 | 340 | 29.5 | 15.1 | 2008 |
| 222 | 341 | 26.9 | 11.4 | 1475 |
| 229 | 379 | 37.3 | 13.5 | 1748 |
| 232 | 427 | 38.9 | 13.4 | 2045 |
| 236 | 396 | 32.1 | 12.2 | 2690 |
| 239 | 372 | 30.5 | 11.9 | 2483 |
| 243 | 384 | 30.7 | 12.1 | 2525 |
| 246 | 259 | 23.5 | 11.1 | 2778 |
| 250 | 277 | 53.2 | 12.5 | 2283 |
| 253 | 390 | 58.1 | 13.2 | 2325 |
| 257 | 358 | 49.5 | 13.3 | 1948 |
| 260 | 114 | 28.1 | 13.8 | 2133 |
| 264 | 196 | 33.3 | 9.1 | 1808 |
| 267 | 215 | 24.0 | 11.6 | 3013 |
| 271 | 251 | 20.3 | 11.8 | 4375 |
| 274 | 253 | 24.8 | 13.0 | 3510 |
| 278 | 259 | 20.7 | 12.5 | 3165 |
| 281 | 264 | 27.4 | 13.1 | 2533 |
| 285 | 275 | 32.1 | 12.6 | 2575 |
| 288 | 134 | 23.6 | 13.8 | 2343 |
| 292 | 304 | 24.1 | 14.0 | 2205 |
| 295 | 300 | 26.8 | 14.1 | 1983 |
| 299 | 319 | 28.8 | 14.1 | 1838 |
| 301 | 284 | 24.3 | 13.9 | 1855 |
| 306 | 334 | 26.9 | 13.5 | 2260 |
| 309 | 323 | 47.6 | 14.8 | 1913 |
| 313 | 352 | 28.6 | 14.1 | 2008 |
| 320 | 329 | 30.8 | 14.7 | 2530 |
| 323 | 301 | 27.1 | 15.1 | 2340 |
| 327 | 287 | 22.7 | 15.1 | 2190 |
| 334 | 310 | 24.5 | 15.2 | 2050 |
| 336 | 283 | 27.4 | 15.9 | 2060 |
| 341 | 254 | 62.1 | 15.8 | 1830 |
| 343 | 235 | 19.9 | 15.7 | 1090 |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Costa, C. A Comprehensive View of the ASM1 Dynamic Model: Study on a Practical Case. Water 2022, 14, 1046. https://doi.org/10.3390/w14071046
Costa C. A Comprehensive View of the ASM1 Dynamic Model: Study on a Practical Case. Water. 2022; 14(7):1046. https://doi.org/10.3390/w14071046
Chicago/Turabian StyleCosta, Carlos. 2022. "A Comprehensive View of the ASM1 Dynamic Model: Study on a Practical Case" Water 14, no. 7: 1046. https://doi.org/10.3390/w14071046
APA StyleCosta, C. (2022). A Comprehensive View of the ASM1 Dynamic Model: Study on a Practical Case. Water, 14(7), 1046. https://doi.org/10.3390/w14071046