Generation of Natural Runoff Monthly Series at Ungauged Sites Using a Regional Regressive Model

Abstract

Many hydrologic applications require reliable estimates of runoff in river basins to face the widespread lack of data, both in time and in space. A regional method for the reconstruction of monthly runoff series is here developed and applied to Sicily (Italy). A simple modeling structure is adopted, consisting of a regression-based rainfall–runoff model with four model parameters, calibrated through a two-step procedure. Monthly runoff estimates are based on precipitation, temperature, and exploiting the autocorrelation with runoff at the previous month. Model parameters are assessed by specific regional equations as a function of easily measurable physical and climate basin descriptors. The first calibration step is aimed at the identification of a set of parameters optimizing model performances at the level of single basin. Such “optimal” sets are used at the second step, part of a regional regression analysis, to establish the regional equations for model parameters assessment as a function of basin attributes. All the gauged watersheds across the region have been analyzed, selecting 53 basins for model calibration and using the other six basins exclusively for validation. Performances, quantitatively evaluated by different statistical indexes, demonstrate relevant model ability in reproducing the observed hydrological time-series at both the monthly and coarser time resolutions. The methodology, which is easily transferable to other arid and semi-arid areas, provides a reliable tool for filling/reconstructing runoff time series at any gauged or ungauged basin of a region.

1. Introduction

Rivers offer several fundamental goods and services to human society and ecosystems. The knowledge of streamflow generated from river basins at different time scales is required for many hydrological applications, including preliminary studies concerning water supply, hydropower, recreation activities, irrigation, and watershed management. Time series recorded at different sites of a region contain crucial information about the spatial, seasonal, and interannual variability of streamflow, which are all basic elements of water resource systems planning and management.

Recent years have been witnessing an increasing qualitative–quantitative degradation of river water due to the coupled effect of human activities (e.g., land use changes or overexploitation of water resources) and climate change. New disciplines, such as socio-hydrology (e.g., [1,2]) or others related to issues of the sustainability and conservation of ecosystems (e.g., [3,4,5,6]), are being developed with the aim of studying the complex mutual interactions between water and society. New efficacious tools are required to reconstruct the natural streamflow of river basins subject to regulation or affected by various anthropic pressures in order to quantify the human-induced alterations of the hydrological regime.

Despite a widespread increment in the density of streamflow gauge networks for many countries across the world, measured flow time series are often limited in sample size or discontinuous, so the majority of the world’s river basins remain ungauged. Another important aspect concerns the quality of data used to force hydrological models: a low data quality, in fact, could represent a further source of uncertainty for models, with important implications for their predictive capability. The growing demand for reliable runoff data in hydrological applications against the recognized lack of available observed data, both in space and in time, has catalyzed the development of a range of methods to estimate streamflow in recent years (e.g., [7]).

Very different methods, each with its strengths and weaknesses, have been developed: from simple empirical and statistics techniques to complex conceptual or physically based rainfall–runoff models. In practical applications, the choice of the most appropriate modeling approach usually depends on the purpose of the modeling, on the temporal and spatial scales of analysis, and, finally, on the data and information availability at the site of interest. The different modeling approaches vary in terms of the complexity with which they are able to simulate the rainfall–runoff transformation processes. Model complexity can often be associated with the number of parameters, which, in turn, is related to both the risk of model over-fitting/over-parameterizing and the need for appropriate spatial/temporal resolution data (e.g., [8,9,10]).

The highest degree of complexity can probably be associated with some distributed and physically based models, such as the SHE [11,12], the IHDM [13], and the tRIBS [14,15], which typically require a high number of parameters with related parameter identification and equifinality problems (e.g., [16]). A high degree of complexity can also be found in some conceptual models, such as the SAC-SMA [17], the AWBM [18], the SIMHYD [19], the IHACRES [20], the TOPDM [21], and the HBV [22], some of which are spatially lumped, with a considerable reduction of model complexity and number of parameters. The simplest rainfall–runoff models, usually used for monthly or larger time scales, are the empirical ones, which usually require the lowest number of parameters. Such methods typically involve the fitting and application of simple equations, which are often derived by regression relationships and relate runoff to other predictor variables such as rainfall, evapotranspiration, temperature, basin elevation, land use, vegetation cover, basin impervious fraction, or streamflow values measured at neighboring gauged basins.

Rainfall–runoff model calibration procedures are essentially data-driven, and, thus, often require observed flow data, which are available only for gauged basins. In order to apply such models to ungauged basins, one must resort to appropriate regionalization techniques defined in regions with consistent hydrological response [23,24]. Several regionalization procedures have been specifically developed for hydrological models (e.g., [25,26,27,28]), including proxy-basin, linear interpolation, and kriging interpolation methods (e.g., [29,30,31,32,33]). The simplest approaches are based on spatial proximity (e.g., [34]) and directly transfer entire parameter sets from the closest gauged catchment to the ungauged basin, by assuming that the two basins behave similarly. More complex approaches are based on physical similarity (e.g., [35]) and try to integrate streamflow information from many other sites in the neighborhood of the basin of interest and additional information on land use, geomorphology, and climate.

Probably the most commonly used approach is based on parametric regression, which consists of developing a posteriori relationships between some physical and climatic basins attributes and model parameters derived at gauged sites. Various attempts have been made to relate, directly or indirectly, model parameters to other basin characteristics, exploiting spatial relationships among streamflow, land use, geomorphology, and different climatic variables (e.g., [36,37,38,39,40,41,42,43,44,45]). Some of the advantages, which are associated with the use of regional regression methods over other more complex methods, are, for instance, mentioned by Hawley and McCuen [46]. An analysis of the applicability and limitations of different regressive models for the estimation of monthly streamflow series was provided by Cutore et al. [47]. In their study two regionalization procedures were compared through application to a Sicilian river basin.

In this paper, a regional regressive model is developed and applied to the entire island of Sicily (Italy). The model is based on a simple, non-linear, regression equation whose parameters can be derived by opportune regional equations as a function of some climatic and physical attributes of the basins. The study involves almost all the gauged basins of Sicily, and encompasses a final validation of six representative basins, not considered during the model calibration.

A first calibration phase involves the definition of a simple model structure, valid across the different basins of the region, and the assessment of “optimal” model parameter sets for all the calibration basins, based on the best agreement between observed and simulated runoff series. The successive phase is aimed to define and calibrate regional regression equations relating such optimal parameters to some significant basin attributes, identified among a set of previously selected possible predictors.

Natural runoff time series are often requested in water resource assessment, water quality, and river ecology studies. This paper proposes a pragmatic solution for the estimation of monthly runoff at ungauged sites, analyzing its applicability and limitations. Model accuracy and robustness are verified through different performance indexes and specific analyses at monthly and coarser time resolutions (i.e., seasonal and annual). The methodology can be easily transferred to other arid and semiarid Mediterranean areas. At the same time, it provides a prompt and reliable tool for the evaluation of the available water resources at any basin of Sicily, a region generally characterized by water scarcity and where similar tools are particularly needed and urgent. The model could also be used in river ecology studies, for example with regard to regulated river basins and with the aim of estimating to what extent the hydrological regime has been modified compared to the natural one.

2. Materials and Methods

2.1. Study Area

The selected study area is the region of Sicily (Italy), which is the largest island in the Mediterranean Sea, with an area of over 25,700 km². Despite the presence of several singularities, the region can be summarily distinguished into three different topographic zones: the northern coast area, mostly mountainous (principal mountain ranges: the Madonie, the Nebrodi, and the Peloritani); the southern coast area, essentially hilly; and the eastern coast area, dominated by the Hyblaean Mountains and the largest active volcano in Europe, i.e., Mount Etna.

The island is characterized by a typical Mediterranean climate, which, according to the Köppen–Geiger climate classification, belongs to the warm temperate class (group: Csa—Hot-summer Mediterranean climate), with, usually, a hot and dry summer and a maximum of precipitation during the colder wintry months. Nevertheless, considerable differences in the thermo-pluviometric regime can be observed among different sub-areas within the region, especially if rainfall and temperature are analyzed at monthly or lower time scales (i.e., daily); in general, the northern coast area is rainier and colder than the southern and eastern coastal areas.

Sicily is drained by several rivers, especially in the central area. The climate and the morphology in the region concur in determining a prevalence of small river basins, usually characterized by non-perennial hydrological regimes. Rivers in the northern coast zone are numerous, short, and ephemeral, while some rivers in the southern cost zone drain wider basins and are perennial. The eastern zone is characterized by some rivers that are relevant in terms of annual discharge. A considerable portion of the region preserves natural conditions in terms of land use: northern Sicily is characterized by the presence of some wide natural areas (e.g., Ficuzza Nature Reserve or Nebrodi Regional Park), where the main forests of the region are settled, while the non-cultivated natural areas in southeastern Sicily are mainly populated by vegetation typical of arid and semi-arid Mediterranean regions.

2.2. Data Sources and Regional Database

The OA-ARRA (Osservatorio delle Acque-Agenzia Regionale per i Rifiuti e le Acque) regional archive provides long historical data series for almost 100 Sicilian river basins, collected by a dense network of gauging stations across the territory (almost 90 hydrometric and 250 meteo-climatic gauging stations). Initially only the basins with at least five continuous years of simultaneous runoff–rainfall–temperature monthly observations have been considered for this study; this reduces the number of examined watersheds to a total of 71 gauged basins (i.e., 39 main basins and 32 sub-basins), as reported in Figure 1a. The assigned identification number (ID), the names of the watershed and the relative hydrometric gauging station, the basin typology (main or sub-basin), and the observation period for each basin are reported in

Table 1. Watersheds and hydrometric gauge station names (St. Name); identification code (ID); typology (Type): main basin (MB) or sub-basin (SB) and sub-zone (A, B, or C); observation period: first and last year of observation and total sample size in years (yr).

ID	St. Name	Watershed	Type		Observations			ID	St. Name	Watershed	Type		Observations
					from	to	yr						from	to	yr
1	Pozzillo	Delia	MB	A	1959	1978	20	37	Passofonduto	Platani	MB	A	1956	1966	11
2	Sparacia	Belice Destro	SB	A	1955	1987	33	38	Mandorleto	S. Biagio	MB	A	1976	1986	11
3	Finocchiara	Senore	SB	A	1961	1986	26	39	Petralia	Imera Mer.	SB	C	1986	1997	12
4	Ponte Belice	Belice	MB	A	1955	1994	29	40	Raffo	Salso	SB	C	1979	1989	11
5	Case Balate	Belice	SB	A	1955	1980	26	41	Regiovanni	Gangi	SB	C	1982	1996	15
6	Piano Scala	Corleone	SB	A	1958	1963	6	42	Castello	Castello	SB	C	1983	1997	15
7	Chinisia	Birgi	MB	A	1971	2001	23	43	Irosa	Alberi	SB	C	1992	2001	10
8	La Chinea	Fastaia	SB	A	1962	1998	35	44	Monzanaro	Salso	SB	C	1985	1997	13
9	Rinazzo	Chitarra	SB	A	1972	1988	17	45	Cinque Archi	Imera Mer.	SB	C	1980	1985	6
10	Lupo	Eleuterio	SB	A	1937	2006	56	46	Capodarso	Imera Mer.	SB	C	1963	1972	10
11	Risalaimi	Eleuterio	MB	A	1961	1990	28	47	Besero	Imera Mer.	SB	C	1959	1966	8
12	Serena	V. dell'Acqua	SB	A	1961	2002	39	48	Drasi	Imera Mer.	MB	C	1960	1970	11
13	Rossella	Eleuterio	SB	A	1937	1957	13	49	Falcone	Elicone	MB	B	1976	1996	18
14	Lentina	Forgia	MB	A	1971	2002	29	50	Passo Gallo	Rosmarino	MB	B	1988	1995	6
15	Scillato	Imera Sett.	MB	A	1976	2003	27	51	Donnapaola	Gibbesi	MB	C	1971	1992	15
16	Fellamonica	Jato	SB	A	1973	2002	18	52	S. Pietro	Ficuzza	MB	C	1974	1994	17
17	Taurro	Taurro	MB	A	1955	1967	12	53	Mazzaronello	Parà Parà	MB	C	1977	1982	6
18	Sapone	Baiata	MB	A	1968	2001	27	54	Castelluccio	Tellaro	MB	C	1974	1998	18
19	Corvo	Magazzolo	MB	A	1972	1979	6	55	Noto	Asinaro	MB	C	1973	1998	15
20	Milicia	Milicia	MB	A	1976	2005	24	56	Manghisi	Cassibile	MB	C	1984	1999	13
21	S.Elia	Modione	MB	A	1972	1981	9	57	S. Nicola	Anapo	MB	C	1972	1998	27
22	Zucco	Nocella	MB	A	1958	2003	42	58	Rappis	Trigona	MB	C	1972	1984	11
23	Parco	Oreto	MB	A	1924	2006	83	59	Reina	Zena	MB	C	1972	1981	10
24	Alcamo Scalo	Freddo	MB	A	1972	1987	10	60	Petrosino	Martello	SB	B	1981	2001	18
25	Monumentale	S. Leonardo	MB	A	1928	1984	55	61	Chiusitta	Saraceno	SB	B	1982	1998	16
26	Vicari	S. Leonardo	SB	A	1924	1987	26	62	Serravalle	Troina di S.	SB	B	1975	2005	23
27	Roccapalumba	Torto	SB	A	1983	2004	21	63	Maccarone	Simeto	MB	B	1975	1982	8
28	Bivio Cerda	Torto	MB	A	1969	2000	18	64	Gagliano	Salso	MB	B	1975	2004	26
29	San Carlo	Sosio	SB	A	1987	2002	13	65	Case Carella	Crisà	MB	C	1958	1986	25
30	Sosio	Sosio	SB	A	1930	1942	13	66	Torricchia	Sciaguana	MB	C	1969	1989	16
31	Poggio Diana	Poggio Diana	MB	A	1934	1939	6	67	Zarbata	Flascio	SB	B	1981	2003	20
32	Ponte Grande	Isnello	SB	A	1984	2000	17	68	S. Giacomo	Alcantara	SB	B	1983	2000	18
33	Guglielmotto	T. dei Mulini	MB	A	1993	2003	11	69	Moio	Alcantara	SB	B	1939	2002	35
34	Ponte Vecchio	Castelbuono	MB	A	1987	2003	17	70	Alcantara	Alcantara	MB	B	1934	2001	32
35	Bruciato	Belici	SB	A	1981	1992	12	71	Ranciara	Forza d'Agrò	MB	B	1983	1993	7
36	Marianopoli	Belici	SB	A	1997	2002	6

. The location of all the OA-ARRA meteo-climatic stations are depicted in Figure 1b, along with reporting information about the station typology (Temperature, Rain–Temperature, or Rainfall gauging stations).

For each basin, historical monthly series of runoff depth at the basin outlet and simultaneous monthly areal precipitation have been retrieved from the official OA-ARRA annual reports (i.e., Annali Idrologici). The corresponding series of mean areal temperature have been estimated starting from the data collected by all the OA-ARRA thermometric stations (Figure 1b) and using the same spatial interpolation techniques used in Pumo et al. [48]; more specifically, algorithms based on a station weighting technique [49,50], which also take into account the elevation, have been used.

The proposed methodology requires a preliminary identification of significant basin descriptors, which could be suitable for the multi-regressive analysis of the second calibration phase. An appropriate basin descriptor selection set may be important in regionalization method performance depending on the adopted regionalization approaches [51]. A preliminary analysis has been carried out for a subset of 20 basins, analyzing several characteristics related to the size, morphology, soils, vegetation, land use, and climate of the basins, and chosen mainly on the basis of their availability and ease of retrieval. In particular, a set of over 30 different basin attributes has been derived from the OA-ARRA regional database or by properly clipping some thematic maps available for the area of interest, such as: a 100-m resolution DEM (Digital Elevation Model) of Sicily (Figure 2a); the Corinne Land Cover Map of Sicily of 2006 [52]; the Soil Map of Italy and Soil Data Base of Italy’s Soil Information System (SISI, [53]); the regional Land Use Map of Sicily (at 1:250,000 scale); the Regional Map of CN (Figure 2b), created in 2004 during the editing of the regional hydrological system plan PAI (Piano di Assetto Idrogeologico) and reporting the Curve Number, i.e., the parameter adopted in the SCS (Soil Conservation Service) Runoff Curve Number method [54].

Such basin attributes, first examined for cross-correlations, were then individually analyzed in terms of their ability to explain the spatial variability of the basin’s hydrologic response; more specifically, the Pearson correlation coefficient has been computed for all the possible combinations of basin attributes (independent variable) and three statistical values (mean, standard deviation, asymmetry) relative to the monthly observed runoff (dependent variable). The least significant explanatory variables have been dropped, selecting only basin attributes with sufficiently high coefficients (over 0.3, significant at 0.05 level) for at least one of the three examined statistics.

Seven basin descriptors have been identified at the end of the selection process and derived for all the other basins (

Table 2. Basin descriptors: MAP = mean annual precipitation; p = seasonal precipitation index; A = drainage area; L = main river length; H = mean basin altitude; z = basin relief; CN = Curve Number.

ID	MAP	p	A	L	H	z	CN	ID	MAP	p	A	L	H	z	CN
	mm/yr	-	km2	km	m a.s.l	m	-		mm/yr	-	km2	km	m a.s.l	m	-
1	678	0.019	138.6	20.91	272	611	80.5	37	620	0.026	1228.6	47.12	519	1140	79.5
2	708	0.018	127.8	32.87	437	946	82.0	38	620	0.012	65.6	14.86	344	449	82.8
3	662	0.019	75.9	23.64	407	1036	79.5	39	760	0.033	28.6	5.63	1220	838	75.9
4	673	0.021	813.9	65.47	439	1398	79.3	40	720	0.017	20.6	3.72	1083	878	79.8
5	717	0.021	338.2	39.27	569	1289	78.7	41	670	0.015	57.6	8.10	858	660	80.6
6	955	0.010	19.4	7.65	805	1087	82.9	42	720	0.026	22.6	4.74	633	259	81.3
7	514	0.020	343.8	36.12	198	767	80.0	43	720	0.035	50.6	18.00	746	561	80.3
8	582	0.027	23.9	7.10	327	465	79.0	44	670	0.041	185.6	18.68	790	1214	80.8
9	475	0.016	37.4	18.12	158	308	79.8	45	630	0.011	545.2	35.34	730	1385	80.2
10	782	0.025	9.7	5.92	796	1078	76.5	46	580	0.037	658.6	50.52	691	1436	80.1
11	793	0.021	55.8	13.10	631	815	76.3	47	600	0.035	1003.6	59.57	634	1496	79.6
12	828	0.020	24.1	10.65	651	745	74.7	48	530	0.033	1887.6	92.18	531	1662	78.7
13	961	0.025	9.3	5.06	651	430	78.1	49	907	0.047	54.6	17.27	696	1249	71.2
14	571	0.020	50.1	23.86	287	906	83.1	50	674	0.073	73.6	10.69	1021	1339	74.0
15	741	0.023	105.2	15.10	837	1612	75.7	51	494	0.032	68.6	15.88	325	212	83.4
16	832	0.018	52.6	14.92	616	1085	78.6	52	512	0.053	101.6	19.53	384	391	76.6
17	786	0.017	166.8	23.38	418	1180	78.7	53	761	0.012	67.6	13.29	461	647	71.6
18	475	0.016	29.1	11.53	111	275	85.5	54	571	0.057	138.6	17.94	456	530	71.9
19	757	0.033	180.1	31.29	531	1352	79.0	55	568	0.036	54.1	14.04	364	494	74.8
20	623	0.029	112.6	17.38	481	912	81.1	56	716	0.053	68.6	14.51	355	511	73.4
21	622	0.026	81.2	26.94	258	609	80.2	57	704	0.041	82.6	15.33	625	538	69.4
22	915	0.024	61.6	14.72	527	1085	74.1	58	588	0.046	71.4	14.96	467	603	57.1
23	1026	0.021	70.4	11.36	601	1206	74.9	59	624	0.050	227.6	27.97	364	888	66.7
24	623	0.021	270.6	32.32	244	741	81.2	60	883	0.045	43.6	9.81	1320	824	65.0
25	699	0.024	498.0	50.73	584	1450	79.4	61	1155	0.035	18.6	5.05	1445	382	69.1
26	704	0.016	246.8	28.23	676	1283	80.2	62	671	0.051	159.4	26.32	969	914	79.2
27	522	0.018	173.3	80.05	570	645	80.7	63	650	0.052	693.6	52.32	1085	2781	73.6
28	537	0.017	415.4	58.32	503	1276	80.4	64	650	0.042	502.6	33.82	791	1150	80.2
29	673	0.031	88.1	19.37	713	1239	73.1	65	642	0.032	50.6	9.95	607	555	81.8
30	899	0.018	106.1	18.16	861	925	77.6	66	429	0.052	63.6	13.60	411	473	78.1
31	833	0.016	391.8	52.90	614	1381	76.7	67	1008	0.043	17.6	4.50	1268	504	67.7
32	795	0.033	34.6	9.67	1229	1368	69.7	68	1034	0.028	35.6	7.69	1258	402	68.5
33	820	0.033	61.6	10.77	1139	1516	72.7	69	842	0.043	306.6	26.37	1117	2619	67.7
34	800	0.036	105.6	21.24	893	1726	73.8	70	919	0.031	557.6	47.50	912	3132	69.4
35	640	0.012	134.6	16.25	606	660	79.3	71	976	0.034	54.6	8.87	688	1012	62.8
36	620	0.031	234.6	20.92	600	675	79.8

): the mean annual precipitation (MAP in mm/year); a seasonal precipitation index (p) given by the ratio between the mean precipitation of August (i.e., usually the least rainy month in Sicily) and the MAP; the drainage area (A in km²); the mean areal Curve Number (CN); the main stream length (L in km); the average altitude (H in m a.s.l.); and the basin relief (z in m), given by the difference between the maximum and minimum elevation of the basin. In particular, parameters representative of the pluviometric regime (MAP and p) have been directly derived from the OA-ARRA database; the topographic features (A, L, H, z) have been derived by the DEM (Figure 2a), while the mean areal Curve Number (CN) was from the Regional Map of CN (Figure 2b).

The basin descriptor set obtained is consistent with other works concerning the regionalization of hydrologic models in Sicily. For example: in Cutore et al. [47], the same attributes H and L were considered together with the permeable soil percentage, which could be considered as a proxy of the variable CN; Viola et al. [55] considered A, MAP, H, CN, and the permeable soil percentage of each basin (not considered here); Cannarozzo et al. [56] used the variables A, L, H, and MAP.

In this study, Sicily as a whole has been initially assumed to be a homogeneous hydro-climatic region. As will be discussed in the following, this kind of approach has successively highlighted the need to consider a more efficient subdivision of Sicily into smaller homogeneous regions. For this purpose, three different sub-zones (A, B ,and C) within Sicily have been considered (Figure 3), using the same subdivisions suggested by Cannarozzo et al. [57] and adopted in Viola et al. [55].

Among the 71 available gauged basins, a total of 18 basins have been excluded from calibration due to different factors. More specifically, 12 basins have been cautiously neglected: some because their runoff series could be affected by regulation due to the upstream presence of artificial reservoirs or diversion dams and, consequently, they cannot be considered representative of natural runoff conditions; and others because some missing data and outliers values have been detected in their hydro-climatic data series. Moreover, a total of six representative basins have been explicitly hidden for validation purposes, selecting a couple of basins, one small (i.e., A < 60 km²) and the other larger (i.e., A > 250 km²), for each of the three considered sub-zones (Figure 4).

2.3. Model Description and Assumptions

The proposed methodology is based on a two-step approach, which refers to two different phases of the calibration procedure. The first step includes the definition of a simple model structure for the creation of regression rainfall–runoff models performing well across all the basins within the study area.

The rainfall–runoff transformation process is usually characterized by complex nonlinear relations, for which the consideration of other interrelated variables could prove to be extremely useful. When snowmelt contributions can be neglected (e.g., arid and semi-arid regions), precipitation occurring during a certain month represents the main water input that, after a series of different hydrological processes, is partially released during the same month as runoff; as a consequence, the runoff results are often significantly correlated with rainfall. In addition to the precipitation, another variable that plays an important role in runoff modeling is the potential evapotranspiration, which represents a control factor for water losses from the soil due to evaporation and transpiration. In practical applications, temperature is often used as a proxy for the potential evapotranspiration [38,47,58], since this is rarely directly measured. Finally, the water accumulated in the soil (both saturated and unsaturated) could influence the slow response of the basins, providing further contributions to runoff generation due to the mechanisms of subsurface and groundwater runoff. This could explain the significant autocorrelation often observed in the runoff time series of basins in arid and semi-arid regions.

A backward analysis of the entire available database has confirmed the conceptual scheme mentioned above: runoff was highly correlated with precipitation and, to a lesser extent, with temperature for all the basins; moreover, in most of the basins, the runoff process was significantly autoregressive. Thus, the following regression-based rainfall–runoff model, suitable for many non-humid regions and already used in a similar way by Cutore et al. [47], has been assumed:

$$\{\begin{array}{ccc}{Q}_k\left(t\right)=a_{1,k}\cdot P_k{\left(t\right)}^{a_{2,k}}\cdot T_k{\left(t\right)}^{a_{3,k}}\cdot Q_k{\left(t-1\right)}^{a_{4,k}}\hfill & if\hfill & Q_k\left(t-1\right)>0\hfill \\ Q_k\left(t\right)=a_{1,k}\cdot P_k{\left(t\right)}^{a_{2,k}}\cdot T_k{\left(t\right)}^{a_{3,k}}\hfill & if\hfill & Q_k\left(t-1\right)=0\hfill \end{array}$$

(1)

where k refers to the analyzed basin, Q_k(t) and Q_k(t − 1) are the monthly natural streamflow values (mm) at the months t and t − 1, respectively, P_k(t) and T_k(t) are the precipitation (mm) and the mean temperature (°C), respectively, at month t, and, finally, a_i,k (with i = 1, 2, 3, 4) are four site-specific model parameters.

The first calibration step requires us to individually calibrate the models, whose general form is given by Equation (1), for all the gauged basins across the region, finding, for each basin, the set of optimal parameters a_i,k associated to the best model reproduction of the observed runoff series.

The second step consists in a regression analysis aimed at identifying a set of four possible regional relationships among such optimal parameters and some, or all, of the previously selected basin descriptors according to the following generic expression:

$$\{\begin{array}{l}{a}_{1,k}=f_1\left[MA{P}_k,p_k,A_k,L_k,H_k,z_k,C{N}_k,|b_{1,1},\mathrm{...},b_{1,m}\right]\hfill \\ \hfill \\ a_{2,k}=f_2\left[MA{P}_k,p_k,A_k,L_k,H_k,z_k,C{N}_k,|b_{2,1},\mathrm{...},b_{2,m}\right]\hfill \\ \hfill \\ a_{3,k}=f_3\left[MA{P}_k,p_k,A_k,L_k,H_k,z_k,C{N}_k,|b_{3,1},\mathrm{...},b_{3,m}\right]\hfill \\ \hfill \\ a_{4,k}=f_4\left[MA{P}_k,p_k,A_k,L_k,H_k,z_k,C{N}_k,|b_{4,1},\mathrm{...},b_{4,m}\right]\hfill \end{array}$$

(2)

where f_i (with i = 1, 2, 3, 4) refers to the generic analytic function describing the regression model found for parameter a_i, for which m regional regressive parameters (i.e., b_i,g with i = 1, 2, 3, 4 and g = 1,…,m) have to be evaluated. The four models of Equation (2) may have a different structure and, consequently, a different number of regional parameters to be estimated for each of them. In particular, the various basin descriptors could have a different weight in explaining the a_i optimal parameters’ variability, and the identification, with consequent exclusion, of those poorly significant could be extremely useful in reducing the number of model parameters [23,24,38]; equifinality and overparameterization are, in fact, common problems for such kind of models and could reduce model robustness, introducing possible sources of model uncertainty. Initially, an attempt to fit a unique model for the entire region was carried out, trying to identify a unique set of equations characterizing the general form of Equation (2); nevertheless, as expected, better results were obtained by separately analyzing the three homogeneous sub-zones of Figure 3 and determining a different set of equations for each of them.

2.4. Calibration Procedure

2.4.1. Regression Rainfall–Runoff Models for the Calibration Basins: Step 1A

The two sequential phases of the calibration procedure are schematically represented in Figure 5. The first step is aimed at identifying the set of parameters a_i,k maximizing the agreement between observed and simulated monthly streamflow series at each calibration basin. The simulated–observed agreement is measured by the Nash–Sutcliffe Efficiency, NSE [59], defined as:

$$NSE=1-\frac{{\displaystyle \sum _{t=1}^N{\left(Q_{emp,t}-Q_{sim,t}\right)}^2}}{{\displaystyle \sum _{t=1}^N{\left(Q_{emp,t}-{\overline{Q}}_{emp}\right)}^2}}$$

(3)

where Q_emp,t and Q_sim,t are the observed (empirical) and the simulated (theoretical) streamflow at the time t, respectively, while ${\overline{Q}}_{emp}$ is the average observed streamflow over the entire sample of observations whose size is N. The NSE values can range between −∞ and 1 (perfect agreement), with positive values generally denoting “behavioral” modeling. Moriasi et al. [60] introduced a performance rating that, for watershed simulations at the monthly time scale, classifies model performances as “satisfactory” for NSE values between 0.50 and 0.65, “good” for NSE between 0.65 and 0.75, and “very good” for NSE over 0.75.

The calibration process has been performed using a specific software tool in Matlab (based on the functions optimset and lsqcurvefit) for unconstrained nonlinear optimization that provides, for the k-th basin, the set of parameters a_i,k corresponding to the highest NSE index (i.e., best agreement). The resulting index can be thought of as the maximum efficiency that the model of Equation (1) can reach at the level of a single basin. The parameters obtained at this calibration phase (named Step 1A) for the 53 different basins are shown in Figure 6, where the optimal values of a_1,k, a_2,k, a_3,k, and a_4,k are represented in four different panels, using different markers for each sub-zone. Despite the use of an unconstrained optimization procedure, the resulting parameters vary among the different basins in very narrow ranges, with positive values for a₁, a₂, and a₄ and negative values for a₃. Given the model structure used (see Equation (1)), this implies that streamflow, at a certain month, is positively correlated to rainfall in the same month and streamflow in the previous month, while it was negatively correlated to the mean temperature in the same month, as expected.

2.4.2. Regional Regression Analysis: Step 1B and Step 2

The second step (Step 2) aims to establish the functional relationships characterizing Equation (2) and relating the set of optimal model parameters to some basin attributes among those previously selected (i.e., MAP_k, p_k, A_k, L_k, H_k, z_k, CN_k).

A first attempt of regionalization has been carried out considering Sicily as a unique homogeneous region and using all seven basin descriptors as predictors in linear regression equations; nevertheless, none of the tested regressive models has provided satisfying coefficients of determination (highest R² equal to 0.26). A general and significant improvement of the same models has been observed considering the region’s subdivision into the sub-zones of Figure 3, even if the value of R² associated with the regression models for the parameter a_1,k remained rather low, especially for sub-zone A (R² = 0.33). For this reason, the value of a₁ has been assumed as constant for each sub-zone and equal to the mean of all the values of a_1,k obtained at Step 1A for each sub-zone. The optimizing procedure of Step 1 has been successively iterated with constant a₁ for each sub-zone, finding a new set of optimal values for a_2,k, a_3,k, and a_4,k for each basin (circles in Figure 7). The parameters assessed during this calibration phase (named Step 1B) are not significantly dissimilar from those obtained at Step 1A and exhibit very similar values in terms of mean, standard deviation, maximum, and minimum over the 53 considered basins.

At Step 2, different linear and nonlinear multiple regressions among the new parameter sets (Step 1B) and the different basin descriptors are analyzed with the objective of finding a unique (i.e., the same structure in the different sub-zones), simple (i.e., few parameters), and efficient (i.e., high R²) regression model for each parameter of Equation (1). An important aspect in multi-regressive analysis is the evaluation of the relative importance of each regressor (i.e., basin descriptors) in explaining the dependent variables’ (i.e., coefficients a_i,k) variance, which allows for identifying a set of only significant covariates, reducing model parameters and, thus, possible sources of uncertainty. To this end, for each parameter a_i,k and for two possible regression model forms (linear or log-linear), the following stepwise procedure has been adopted: (1) several models are set by adding, in successive steps, a certain predictor to all the possible subsets of the remaining predictors; (2) each model is fitted for each sub-zone by the ordinary least squares method; (3) the mean value of the coefficient of determination R² over the three sub-zones is associated to each model; (4) the relative weight of that predictor is given by the average R² over all the tested models; (5) the procedure is iterated for all seven basin descriptors; (6) descriptors explaining less than 5% of the dependent variables variance are rejected, while the remaining ones are considered. At the end of this procedure, the following linear regressive models have been obtained:

$$\{\begin{array}{l}{a}_{1,k}=b_{1,1,Z}\hfill \\ \begin{array}{l}{a}_{2,k}=b_{2,1,Z}+b_{2,2,Z}\cdot MA{P}_k+b_{2,3,Z}\cdot p_k+b_{2,4,Z}\cdot H_k+b_{2,5,Z}\cdot C{N}_k\\ a_{3,k}=b_{3,1,Z}+b_{3,2,Z}\cdot MA{P}_k+b_{3,3,Z}\cdot p_k+b_{3,4,Z}\cdot H_k+b_{3,5,Z}\cdot C{N}_k\\ a_{4,k}=b_{4,1,Z}+b_{4,2,Z}\cdot A_k+b_{4,3,Z}\cdot z_k+b_{4,4,Z}\cdot H_k+b_{4,5,Z}\cdot C{N}_k\end{array}\hfill \end{array}$$

(4)

where the symbol Z refers to the sub-zone (Z = A, B, or C) of the k-th basin, while b_i,j,Z (with i = 1, 2, 3, 4; j = 1, 2, 3, 4, 5) are 16 regional regression parameters, estimated for each sub-zone by the least squares method and reported in

Table 3. Regional regression parameters b_i,j,Z for the estimation of the parameters a_i,k by Equation (4).

Regional Regression Parameters for a1,k
sub-zone (Z)	b1,Z
A	0.20503
B	0.24834
C	0.24138
Regional Regression Parameters for a2,k
sub-zone (Z)	b2,1,Z	b2,2,Z	b2,3,Z	b2,4,Z	b2,5,Z
A	4.21951	−0.00062	−7.61813	−0.00063	−0.02503
B	1.08348	−0.00034	−3.50405	−0.00007	0.00567
C	−0.16628	0.00106	−6.65375	−0.00060	0.01663
Regional Regression Parameters for a3,k
Sub-zone (Z)	b3,1,Z	b3,2,Z	b3,3,Z	b3,4,Z	b3,5,Z
A	−5.00350	0.00146	8.75665	0.00076	0.03254
B	0.29398	0.00030	2.14731	0.00013	−0.01299
C	1.64497	−0.00200	21.68726	0.00140	−0.03573
Regional Regression Parameters for a4,k
sub-zone (Z)	b4,1,Z	b4,2,Z	b4,3,Z	b4,4,Z	b4,5,Z
A	−1.13660	−0.00002	−0.00003	0.00033	0.01651
B	0.28308	−0.00018	0.000004	0.00016	−0.00164
C	0.35555	0.00014	−0.00027	0.00021	0.00119

. With this structure, the three parameters a_2,k, a_3,k, and a_4,k of the rainfall–runoff model of Equation (1) are all dependent on the basin mean altitude and mean areal curve number (H_k and CN_k, respectively) and other two basin descriptors; more specifically, the exponents for the climatic variables P_k(t) and T_k(t) in Equation (1) (i.e., a_2,k and a_3,k, respectively) are both also related to the basin pluviometric regime descriptors MAP_k and p_k, while the exponent (i.e., a_4,k) for the previous month’s runoff, Q_k(t − 1), is derived as a function of the basin drainage area (A_k) and the relief (z_k), two basin attributes that influence the streamflow transferring process toward the basin outlet and whose variability among the different basins could influence the lag-1-month autocorrelation in the corresponding streamflow series.

The ability of the nine regression models of Equation (4) to reproduce the optimal values of a_i,k (with i = 2, 3, 4) derived at Step 1B, measured by the R² coefficient, ranges from 0.41 (model for a_4,k in the sub-zone A) to 0.90 (model for a_3,k in the sub-zone C), with a mean R² of 0.67. The mean value of R² associated to the three equations for each sub-zone is equal to 0.58 for sub-zone A, 0.73 for sub-zone B, and 0.70 for sub-zone C.

The regionalized values of a_2,k, a_3,k, and a_4,k for all the calibration basins (model parameters at Step 2), obtained by Equation (4) with the regression parameters of Table 3, are also reported in Figure 7 and compared with the parameter values resulting after Step 1B. The parameters at Step 1B (optimal) and Step 2 (regionalized) have almost the same mean value over the 53 basins, with differences below 3%, while the variance of the regionalized parameters is reduced by about 16% for a_2,Z and a_3,Z and by 34% for a_4,Z. The most significant variation between the parameters before and after regionalization can be noticed for parameter a_3,Z, with a maximum at the basin with ID 59 (sub-zone C) where the regionalized value results are one order of magnitude higher than the corresponding optimal parameter at Step 1B.

3. Results and Discussion

3.1. Model Performances for the Calibration Basins

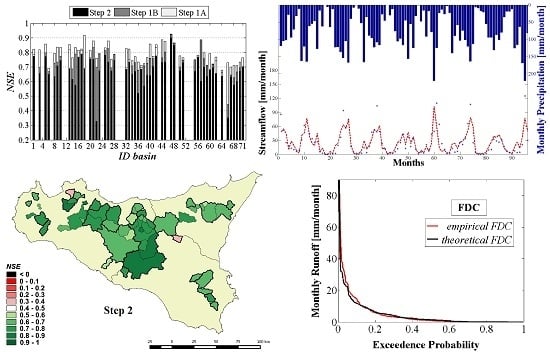
The model in Equation (1), with the four parameters individually calibrated for each site (Step 1A, Figure 6), has shown, over the 53 calibration basins, a high capacity for reproducing observed streamflows, with NSE values ranging from 0.64 to 0.93 and a mean of 0.77 (

Table 4. (a) Analysis of NSE indexes (mean for sub-zone, and mean, standard deviation, minimum, and maximum over all the calibration basins) at the different calibration stages (Step 1A, Step 1B, Step 2); (b) Analysis (mean, standard deviation, minimum, and maximum) of other performance indexes (ME = mean error; ME/${\overline{Q}}_{emp}$ = dimensionless mean error; RMSQ = root mean square error) over the calibration basins after the regionalization (Step 2). The basin ID codes corresponding to the best, minimum, and maximum performance indexes are also reported within brackets.

(a)	Mean NSE for Sub-Zone			NSE (53 Calibration Basins)
Calibration Stage	A	B	C	Mean	St. Dev.	Min (ID)	Max (ID)
Step 1A	0.78	0.71	0.80	0.77	0.066	0.64 (68)	0.93 (47)
Step 1B	0.77	0.69	0.77	0.75	0.080	0.44 (66)	0.92 (47)
Step 2	0.69	0.65	0.70	0.69	0.100	0.32 (22)	0.90 (47)
(b)				Step 2 (53 Calibration Basins)
Model Statistics				Mean	St. Dev.	Min (ID)	Max (ID)	Best (ID)
ME (mm/month)				0.28	3.74	−8.32 (39)	11.03 (40)	0.113 (1)
ME/${\overline{\mathit{Q}}}_{\mathit{e}\mathit{m}\mathit{p}}$				−0.02	0.21	−0.69 (66)	0.35 (40)	0.009 (1)
RMSE (mm/month)				16.46	10.00	3.74 (48)	46.55 (61)	3.74 (48)

a). The NSE values for such basins are represented in the histogram of Figure 7 (upper-left panel) and in the map of Figure 8a. From the latter as well as the results synthesized in Table 4a, it can be observed that the model in sub-zone C provides, on average, higher performance than results in the other two sub-zones.

The assumption that a₁ is constant for each sub-zone has provided new sets of optimal values for a_2,k, a_3,k, and a_4,k (Step 1B) whose corresponding performance, in terms of NSE, is reported in the same histogram of Figure 7 and Table 4a. The results are quite similar to those previously discussed (Step 1A), denoting a not significant decrease in the model’s performances; on average, a reduction in the order of 2% for the NSE indexes can be noticed. A significant NSE reduction (from 0.73 to 0.44) has been detected only for the ID 66 basin (sub-zone C), which is characterized by the lowest value of MAP and the second highest value of p.

As expected, the use of the regional relationships in Equation (4) for the a_i,k parameter assessment (Step 2), reduces model performance with respect to the adoption of optimal (Steps 1A and B) parameter sets (histogram of Figure 7). Actually, this performance reduction is a price that has to be paid in order to provide a procedure able to assess runoff at ungauged sites. Nevertheless, the final model performances (after the Step 2) (Table 4a) remain in the range of acceptable values in terms of NSE, i.e., performance equal or more than satisfactory, according to the performance rating of Moriasi et al. [60], for all the calibration basins; the only two exceptions are the abovementioned ID 66 basin (sub-zone C), which had the lowest starting NSE value (i.e., NSE = 0.44 at Step 1B), and ID 22 basin (sub-zone A), where the resulting values are, however, positive and equal to 0.33 and 0.35, respectively. For this last basin, model performance reduction after the regionalization procedure is rather consistent, since, after Step 1B, the NSE was quite high (0.77). This could be attributable to the fact that the parameter values derived for this basin after Step 2 are markedly different from the corresponding values obtained at Step 1B, especially with regard to the parameter a₄, whose regionalized value results were halved with respect to the previously obtained optimal value (from 0.43 to 0.23).

The percent reduction of the NSE after the regionalization, with respect to the NSE computed at the Step 1B, ranges from 0.17% to 57%, with the mean NSE (=0.69) over all the calibration basins reduced by almost 9% and denoting overall good performances. The efficiency reductions after the regionalization with respect to Step 1A are slightly more marked, with NSE reduced by 11% on average. This comparison is also emphasized in Figure 8, where the NSE obtained with the regionalized parameters (Figure 8b) and with the parameter sets of Step 1A (Figure 8a) are represented by the same color bar. Also, after the regionalized procedure, the model exhibits, on average, a higher accuracy for the basins in sub-zone C, with a mean NSE of 0.70 (Table 4a). The ID 47 basin (sub-zone C) has shown the highest NSE at every calibration phase (Table 4a), with a performance reduction after the regionalization (Step 2) equal to about 3%.

Model performances at Step 2 have also been assessed using three further statistical criteria measuring the agreement between observed and simulated monthly streamflow series: the mean error, ME (in mm/month); the dimensionless mean error, ME/${\overline{Q}}_{emp}$, given by the ratio between the ME and the average observed streamflow (${\overline{Q}}_{emp}$); and the root mean square error, RMSE (in mm/month). For each index, the mean, the standard deviation, the minimum, the maximum, and the best values over all the calibration basins are synthesized in Table 4b. The results of this analysis have confirmed the outcomes relative to the performance index used for calibration (i.e., NSE), confirming the validity of the adopted calibration procedure. The model has globally provided a satisfying accuracy in terms of all the analyzed indexes and can be considered unbiased, as demonstrated by the relatively low values of ME. The values of ME, in absolute value, are lower than 3 mm/month for about 80% of the analyzed basins, while the mean ME/${\overline{Q}}_{emp}$ over the calibration basins is almost null. In terms of RMSE, the indexes have been of the same order of magnitude as those found through a similar modeling approach by Cutore et al. [47] for the Simeto river sub-basins (Sicily, Italy), with the worst performance (about 45 mm/month) obtained at basins ID 61, 67, and 68, which are all basins corresponding to NSE values lower than the mean value (0.69, 0.63, and 0.58, respectively).

The basin with the highest NSE (i.e., ID 47) also provided satisfactory performance in terms of ME, ME/${\overline{Q}}_{emp}$, and RMSE (0.428, 0.042, and 5.05 mm/month, respectively). The basins with the lowest NSE (i.e., ID 22 and 66), showed the worst performance with respect to the other considered statistical criteria (ME = −6.67 and −2.54 mm/month, ME/${\overline{Q}}_{emp}$ = −0.49 and −0.69, RMSE = 15.37 and 9.97 mm/month, respectively). Only one basin (ID 40; sub-zone C) associated with a satisfying NSE (0.63), even if it was below the mean of the other basins, has provided relevant values for ME (11 mm/month) and ME/${\overline{Q}}_{emp}$ (0.35), denoting a weak performance that is, however, comparable to the worst performance obtained in different studies (e.g., [47]).

A comparison between monthly flow duration curves (FDCs) based on observed and simulated runoff values is reported in Figure 9 for different representative basins. Four examples, referring to basins with performance indexes approximately equal to the averages over all the calibration basins, are reported: basin ID 18 can be considered representative of basins with mean NSE, basin ID 42 is representative of basins with mean ME, basin ID 25 is representative of basins with mean ME/${\overline{Q}}_{emp}$, while basin ID 59 is representative of basins with mean RMSE. Moreover, since the FDCs typically depend on the period considered, a comparison of the basins with the shortest (ID 45) and the longest (ID 23) sample size is also reported. Although some important details of the variations in flows can be obscured when the FDCs are computed using monthly data, rather than daily or finer resolution data, this analysis has been useful in confirming model accuracy. For all the examined basins, in fact, the model has satisfactorily reproduced the magnitudes associated with the various observed monthly runoff values, from the lowest and more frequent values to the highest and rarer ones, proving to be effective also in the assessment of the probability that a certain runoff value will be equaled or exceeded.

3.2. Model Validation

Model validation has been carried out by applying the model to the six validation basins (i.e., ID = 12, 24, 43, 46, 49, and 63; Figure 4) previously selected and not considered during the calibration (two of different area for each sub-zone). For each of them, the entire available historical monthly streamflow series has been reproduced by the model and compared with the corresponding empirical series, analyzing model performances through the same indexes previously used.

Performance achieved in the validation phase, summarized in

Table 5. Model performances (NSE, ME, ME/${\overline{Q}}_{emp}$, RMSQ) at the monthly scale for the validation basins. The identification number (ID), the sub-zone, the area (A), the simulated–observed series size in years (Size), and the observed mean annual precipitation (MAP) are also reported for each basin.

Validation Basins					Monthly Performance Indexes
ID	Sub-Zone	Size	A	MAP	NSE	ME	ME/${\overline{Q}}_{emp}$	RMSE
		(yr)	(km2)	(mm/yr)		(mm/month)		(mm/month)
12	A	39	24.1	828	0.70	−5.01	−0.30	16.19
24	A	10	270.6	623	0.76	0.53	0.05	14.44
49	B	18	54.6	907	0.71	0.38	0.02	18.22
63	B	8	693.6	650	0.74	−1.79	−0.11	11.67
43	C	10	50.6	720	0.73	−0.83	−0.11	7.85
46	C	10	658.6	580	0.79	0.30	0.03	6.95

, was similar among the different basins and very close to that measured at the calibration basins, with high NSE values (mean NSE = 0.74) and low ME, ME/${\overline{Q}}_{emp}$ and RMSE for all the six basins. Model series reproduction in the larger basins (ID 24, 63 and 46) was slightly more accurate (mean NSE = 0.79) than in the smaller ones (mean NSE = 0.71), but no significant difference can be noticed among model performances in validation over the different sub-zones. The results indicate the best performances (i.e., best NSE and RMSE) at the ID 46 basin (sub-zone C), with a sample size of 10 years, while the lowest performance was at the rainiest basins (ID = 12 and 49), characterized by the longest series (39 and 18 years, respectively).

Despite the fact that the validation basins are characterized by marked differences in terms of rainfall–runoff transformation, with mean annual runoff coefficients ranging from 0.14 (ID 43) to 0.34 (ID 49), the model has shown, over the six basins, an equal ability to capture the different basins’ hydrological response, with performance that can be classified as “good” in all the basins and, for two cases (i.e., basins ID 24 and 46), even as “very good” (i.e., NSE > 0.75).

Figure 10 depicts a comparison between observed and simulated monthly specific streamflow series (mm/month) for the six validation basins, also reporting the corresponding precipitation series. Simulated series are quite close to the observed series, reproducing well most of the peaks and null values. Despite the marked differences, in terms of both observed rainfall and streamflow, that can be noticed among the basins, the model captures rather accurately the monthly streamflow variability for both the smaller (left panels) and larger (right panels) basins in the three sub-zones. For example, the ID 12 basin is characterized by a seasonal streamflow regime, with about five months per year almost dry and frequent winter peaks with streamflow of about 100 mm/month, while the ID 24 basin is characterized by more regular behavior in the observed streamflow, with, on average, less rainfall and streamflow, and with only five months out of eight years having streamflow on the order of 100 mm/month; for both basins the model showed similar performance.

3.3. Model Performances at Different Aggregated Time Scales

Model performances have been further evaluated at different temporal aggregations, also considering the seasonal and the annual time scales. This analysis has been performed with regard to both the 53 calibration basins and the six validation basins, considered as a unique sample. More specifically, simulated monthly streamflow has been aggregated at the annual scale and also at the seasonal scale, considering the year as divided into two seasons: dry season, from April to September, and wet season, the remaining six months of the year.

Figure 11 compares all the estimates of the monthly, annual, and seasonal streamflow obtained from the regional model for all the basins with the corresponding observed streamflow. In the top left panel of the figure, a total of 12,312 theoretical monthly streamflow estimates are plotted against the corresponding empirical values, while the other scatter diagrams on the top refer to the annual streamflow values (middle panel, 1026 values) and the mean annual totals of streamflow for each basin (right panel, 59 values). In the bottom panels of Figure 11, the empirical and theoretical dry season (left panel), wet season (middle panel) streamflow values and the mean seasonal totals of streamflow for each basin (right panel) are similarly compared.

The high predictive ability of the model at the different aggregation scales is demonstrated by the fact that, for all the plots, most of the points are rather close to the perfect agreement lines (also reported in all the graphs), with high values of the coefficient of determination R². These values are greater than 0.92 at the monthly level and 0.90 at the annual level. At the seasonal level, the model reproduces the dry season streamflow with an R² of 0.95 and the wet season values with an R² of 0.90. Although the cloud of points appears to be more disperse than in the other plots, the high value of R² obtained at the monthly scale can be explained by the presence of a considerable number of observed values that are identically reproduced by the model (i.e., 22% of the null values and about 5% of the not-null streamflow).

Satisfying model performance has also been obtained with regard to the reproduction of the mean annual and seasonal totals of streamflow for the different basins (right panels of Figure 11), as is demonstrated by the resulting high R² values (i.e., 0.95, 0.89, and 0.92 for the dry season, the wet season, and the annual analysis, respectively) and the low mean percent errors (from 2.2% for the annual and the wet season, to 12.5% for the dry season). The best performance in terms of absolute error (AE) was obtained at the basins with ID 42 for the dry season (AE = 0.21 mm/season), ID 37 for the wet season (AE = 0.02 mm/season), and ID 45 for the annual analysis (AE = 0.34 mm/season), while the worst resulted at basins with ID 56 for the dry season (AE = 65 mm/season), and ID 40 for the other two aggregation periods (AE = 121 mm/season and 135 mm/year for the wet season and the year, respectively). These values are consistent with results previously obtained at the monthly scale, where the ID 40 basin showed the worst performance in terms of both ME and ME/${\overline{Q}}_{emp}$ (Table 4b).

The results represented in Figure 11 have, therefore, demonstrated an elevated model capacity to reproduce not only the runoff at the monthly scale but also at coarser time resolutions, showing a satisfying ability to also reproduce the seasonal and interannual variability. A noteworthy aspect is that, despite the use of different models for the three subzones (i.e., same model structure and different regression parameters for each) and the application under 59 different boundary conditions (i.e., 59 different basins), all the estimates, at all the analyzed aggregation time scales, have shown comparable error, as can be observed from the left and middle panels of Figure 11.

Also at coarser time resolutions, model performances in validation basins have results comparable with those relative to the calibration basins, with similar residual errors. The analysis at the annual time scale for the validation basins has been further deepened by comparing simulated and observed annual streamflow series and computing all the different performance indexes previously used at the monthly scale. The results of this analysis, together with a comparison between empirical and theoretical values for the main annual statistics (mean, standard deviation, minimum, and maximum), are synthesized in

Table 6. Model performances (NSE, ME, ME/${\overline{Q}}_{emp}$, RMSQ) at the annual scale for the validation basins. The observed (Emp.) annual statistics (mean, standard deviation, minimum, and maximum) are also compared with the corresponding simulated (Theo.) values.

Validation Basins: Annual Statistics										Annual Performance Indexes
ID	Sub-Zone	Mean		St. Dev.		Min		Max		NSE	ME	ME/${\overline{Q}}_{emp}$	RMSE
		(mm/yr)		(mm/yr)		(mm/yr)		(mm/yr)			(mm/yr)		(mm/yr)
		Emp.	Theo.	Emp.	Theo.	Emp.	Theo.	Emp.	Theo.
12	A	204	263	128	129	17	72	555	628	0.64	−58.36	−0.29	75.53
24	A	129	123	203	113	22	53	586	375	0.79	6.62	0.05	86.54
49	B	306	300	135	94	164	185	748	586	0.86	6.10	0.02	49.62
63	B	186	217	87	63	108	144	349	338	0.68	−30.62	−0.16	45.70
43	C	98	108	91	88	20	51	306	320	0.96	−9.98	−0.10	17.55
46	C	126	121	27	29	92	62	158	160	0.26	5.35	0.04	21.90

.

For most of the cases, all the simulated main annual statistics are very close to the observed ones; moreover, it can be noticed that the reproduced variability is essentially never higher than that observed. The annual performance indexes show a good agreement between simulated and observed annual streamflow series: the highest NSE (0.96) was reached for the ID 43 basin, while the NSE values for the other basins are all higher than 0.64, with the only exception being the ID 46 basin, where a relatively low efficiency (NSE = 0.26) was obtained due to a low variance of the observed series that could negatively affect the NSE representativeness (see Equation (3)). Other indexes, in fact, denote good model performance at the ID 46 basin, while the ID 12 basin had the lowest performance, with values for ME and ME/${\overline{Q}}_{emp}$ slightly outside the ranges obtained for the other basins and also a relatively high value for RMSE.

4. Conclusions

This study applies a regional regressive model for the reconstruction of natural runoff series at the monthly or coarser time resolutions, intensively analyzing its performance. The importance of developing appropriate and easily transferable rainfall–runoff models able to reproduce reliable and long runoff series from climatic data is related to the fact that, in many practical cases, a runoff dataset is not available or insufficient in size, while long data series of climatic variables are much more often available, and, then, can be exploited to fill gaps in runoff records. A practical means of estimating natural runoff dynamics at ungauged stream sections or for rivers subject to regulation is fundamental for a variety of modern hydrological applications that involve a number of sectors (e.g., engineering, economic, environmental, etc.).

The idea proposed in this paper is to implement a calibration procedure for rainfall–runoff models based on the knowledge of “soft” basins information, usually available, such as rainfall, temperature, morphology, or land use. The model has been calibrated, through a simple two-step procedure, for the island of Sicily using a considerable number of basins and it has been validated in six basins representative of different basin sizes and different climatic subareas within the examined region.

This application may be considered as a benchmark for similar hydrological and climatic areas. Through a detailed description of the adopted methodology, some practical aspects that may be of interest for the model’s application to other regions have been explored. For instance, in this study, model performance has been revealed to be higher if the region is considered as divided into three different sub-zones. Moreover, six different basin attributes have been demonstrated to be functional in the definition of opportune regional equations for the estimation of the rainfall–runoff model parameters. The same methodology, applied to arid and semi-arid regions different from the study area of this work, could converge towards a different subdivision of the area of interest and/or different regional equations, characterized by different basin descriptors; nevertheless, the adopted structure for the rainfall–runoff models, which has shown extremely high accuracy at all Sicilian basins before the regionalization step, is expected to be equally valid. On the contrary, the application to humid regions should also encompass a redefinition of a more suitable conceptual scheme for the regression model, even if the proposed methodological approach could equally be followed.

For all the basins analyzed in this study, the regionalized model has shown satisfying accuracy, measured by different performance indexes, in reproducing the observed runoff at different time scales from monthly to aggregated seasonal and annual scales. Considering the Nash–Sutcliffe Efficiency (NSE) for the monthly series reproduction, it was rather weak for only two cases, but nevertheless positive (>0.33), denoting a “behavioral” modeling, while the NSE indexes for the other basins were all over 0.50, with “satisfactory” performance for 21% of cases, “good” for 53%, and “very good” for the remaining 26%, according to the performance criteria given by Moriasi et al. [60]. At coarser time resolutions, model performance did not show significant variations, with a very low percentage of error in the reproduction of both the seasonal and the annual mean runoff in any basin and an ability to also capture the seasonal and interannual runoff variability. The robustness of the model is strongly confirmed by the results in validation, in which a model reproduction of the historical runoff series at all the tested time scales gave results comparable to those obtained in calibration.

The obtained results have demonstrated how the model discussed in this study can be seen as a prompt and suitable option for the estimation of natural runoff time series at ungauged sites. It is worth emphasizing that an important application of the model is currently under development. In particular, a specific plug-in is being implemented within open-source GIS software (i.e., Quantum GIS 2.10) with the aim of automatizing data retrieval and processing procedures. After a preliminary preparation of an opportune Database Management System (DBMS) supporting the plug-in, the regional model, entirely re-coded in Python scripting language, will be able to rapidly assess natural runoff series (at monthly or higher time scales) for any basin of Sicily and any desired time window, both selected by an opportunely implemented Graphical User Interface (GUI). The plug-in will be based on a Data Processing Module (DPM), which, using spatial analysis techniques, will first proceed with the watershed classification (i.e., into sub-zones) and delineation, derivation of the monthly time series of mean areal precipitation and temperature, extraction of the six basin descriptors needed for the model and, then, derivation of the monthly runoff time series.