A Novel Multimodal Biometrics Recognition Model Based on Stacked ELM and CCA Methods

Abstract

Multimodal biometrics combine a variety of biological features to have a significant impact on identification performance, which is a newly developed trend in biometrics identification technology. This study proposes a novel multimodal biometrics recognition model based on the stacked extreme learning machines (ELMs) and canonical correlation analysis (CCA) methods. The model, which has a symmetric structure, is found to have high potential for multimodal biometrics. The model works as follows. First, it learns the hidden-layer representation of biological images using extreme learning machines layer by layer. Second, the canonical correlation analysis method is applied to map the representation to a feature space, which is used to reconstruct the multimodal image feature representation. Third, the reconstructed features are used as the input of a classifier for supervised training and output. To verify the validity and efficiency of the method, we adopt it for new hybrid datasets obtained from typical face image datasets and finger-vein image datasets. Our experimental results demonstrate that our model performs better than traditional methods.

1. Introduction

The field of biometrics has gained attention globally because of its broad application prospects, and huge social and economic benefits. However, it could affect the performance of a single-mode biometric identification system that has biometrically detected “noise” (such as a fingerprint with a scar or a changed voice due to a cold). A solution known as the fusion strategy of multimodal biometrics or multi-biometrics has been found, and it represents a contemporary trend [1].

Deep learning is a promising study of machine learning, and it has recently gained more attention. Many studies show that a deep network with a multiple hidden-layer neural network architecture has the advantage of mining effective information fully for data, and it can also successfully achieve unsupervised learning of single-mode data (text, images, voice, etc.) [2], which inspires the multimodal deep learning.

An important prerequisite for multimodal deep learning is the extraction of a hybrid mode. Many works have been made for modal fusion. For example, Liu et al. [3] proposed multimodal stacked auto-encoders for a video classification task, which models image, audio, and text for joint features of the signal. Ngiam et al. [4] regarded the sparse restricted Boltzmann machines as a basic unit of the model and introduced the idea of the auto-encoder to learn the joint characteristics of video and audio input and further applied it to the audio-visual language classification for isolation of letters and numbers. Srivastava et al. [5] learned multimodal data expression via the Deep Belief Network model, which mapped multi-data to a joint hidden expression layer and defined a joint density model on the multimodal input space to fill in the missing data. All the mentioned multimodal deep-learning models can obtain satisfactory performance but are inevitably influenced by the negative impact of the back propagation algorithm on generalization performance and learning speed [6].

Meanwhile, extreme learning machines (ELMs) [7], with their fast learning speed and efficient computational efficiency, have attracted more attention than the traditional deep-learning methods. ELMs prevents the disadvantages of the BP algorithm and obtains robust feature representation. Therefore, we present the novel concept of stacked ELMs, which simply uses an ELM as the learning unit. It inherits both advantages of auto-encoder’s computational efficiency and ELM’s fast learning speed.

The second challenge in the multimodal biometric system lies in effective feature fusion. Data fusion consists of three levels—pixel-level, feature-level, and decision-level. Paul et al. [8] introduced a decision fusion for multimodal biometric systems using Social Network Analysis (SNA), which was utilized to reinforce the confidence level of the classifier to reduce error rate. Haghighat et al. [9] presented the Discriminant Correlation Analysis (DCA), a feature-level fusion technique that incorporates class associations during the correlation analysis of the feature sets. A fusion method may boost recognition rates but also cause greater consumption of calculation. More studies about simple but effective fusion method have been conducted.

The Canonical Correlation Analysis (CCA) method can calculate the relationship between two sets of variables. The principle of CCA is described as follows: It selects a representative comprehensive index (a linear combination of the variables) from two groups of random variables; the correlation of the index can represent the relationship between the original two sets of variables; and that relationship can be reasonably simplified in the process of the correlation analysis of the two groups. We hold that applying the CCA method on a multimodal biometric image to construct the multimodal image’s shared feature space and to reconstruct multimodal image characteristics is an effective means of finding out cross-modal characteristics. So, we take the CCA method into consideration and treat it as our feature-level fusion strategy.

The rest of this paper is arranged as follows: Section 1 introduces the basic theory of related research methods. Section 2 describes our proposed novel method with its algorithm description. Section 3 verifies the algorithm performance via several experiments and the subsequent analysis of the experimental results. Section 4 summarizes the proposed approach and introduces new ideas for future research.

2. Materials and Methods

2.1. Related Work

This section presents the basic theory of the relevant research methods used in our paper—the ELM and CCA methods.

2.1.1. The ELM Method

The ELM method was proposed by Huang Guangbin of Nanyang Technological University [10]. This method is used to solve the single hidden-layer neural network algorithm. Traditional neural network learning algorithms (such as the BP algorithm) need to obtain a large amount of network training parameters and easy-to-produce local optimal solutions. In contrast, an ELM has a duty to only set the number of hidden-layer nodes of networks and not to adjust the network weights of the input and hidden bias. Thus, the ELM method takes advantages of fast learning speeds and good generalization capability. A feed-forward neural network with L hidden-layer nodes is described below:

$$f_L(x)={\displaystyle \sum _{i=1}^L{\beta }_{i}G({W_i}^{*}{X}_j+b_i)=h(x)\mathsf{\beta }},j=1,\cdots ,N$$

(1)

where $G(·)$ is the activation function, $X_j$ denotes the jth sample, $W_i$ is input weight, ${\beta }_i$ is output weight, $b_i$ is bias, and $h(x)$ is the output of the hidden layer.

Algorithm 1 summarizes the ELM algorithm.

Algorithm 1. The extreme learning machine (ELM) algorithm.

Input: training set $\mathsf{\delta }=\left\{\left(x_i{t}_i\right)\right|\left(x_i\in R^n,t_i\in R^m,i=1,\dots ,N\right)\}$, activation function $g\left(x\right)$ and hidden-layer node number n

Output: the output weight β

Step 1: Randomly assign input weight $w_i$ and bias $b_i$

Step 2: Calculate the hidden-layer output matrix $\mathrm{H}$.

Step 3: Calculate the output weight β. $\beta =H^{†}*T,$ where $T={[t_1,\cdots ,t_N]}^T$

In the algorithm mentioned above, the method used to calculate $H^{†}$ (the Moore–Penrose matrix of the hidden-layer output matrix $H$) is orthographic projection: that is, when $H^{T}H$ is nonsingular, $H^{†}={(H^{T}H)}^{-1}{H}^T$; when $H{H}^T$ is singular, $H^{†}=H^T{(H{H}^T)}^{-1}$. According to the principle of ridge regression, during the calculation of $H^{†}$, a smaller positive number $\frac{1}{\lambda }$ is introduced on the diagonal of $H{H}^T$ or $H^{T}H$ as a regularization item, which improves the generalization performance of the extreme learning machine. Therefore, in the regularization-based ELM:

When the number of training samples is greater than the number of hidden-layer nodes, the output weight matrix $\hat{\beta }$ can be calculated by following equation:

$$\hat{\beta }={(\frac{1}{\lambda }+H{H}^T)}^{-1}{H}^{\mathrm{T}}T,N>n_h$$

(2)

Otherwise, when the number of training samples is less than the number of hidden-layer nodes, the output weight matrix $\hat{\beta }$ calculation formula is:

$$\hat{\beta }={(\frac{1}{\lambda }+H{H}^T)}^{-1}{H}^{\mathrm{T}}T,N>n_h$$

(3)

Compared with traditional gradient-based algorithms, the ELM algorithm has two significant benefits. Firstly, it learns faster than most of the traditional learning algorithms. Secondly, all of the network parameters in the ELM algorithm do not need to adjust except for the number of hidden-layer node. Furthermore, the ELM algorithm can always search for the optimal solution directly with no fitting problem. These features make the ELM method more flexible and appealing than the traditional gradient-based algorithms. Recent studies show broad application prospects for the ELM algorithm. For example, Xie et al. [11] applied the ELM method to projective feature learning for 3D shapes. Akusok et al. [12] applied a tool box of ELM algorithms for big-data application.

2.1.2. The CCA Method

The CCA method was suggested by Harold Hotelling [13]. It is a multivariate statistical analysis method, which uses the correlation between the comprehensive variable pairs to reflect the overall correlation between two groups of indicators. Its basic principle is described as follows: in order to obtain the relevant relationship between the two groups of indicators on the whole, it extracts two representative aggregate variables, U1 and V1 (which is a linear combination of the variables in the two-variable set), from the two groups of variables. It then uses the relationship between the two variables (U1 and V1) to reflect the overall correlation between the two groups of indicators [14].

The CCA method is the most commonly used algorithm for data mining [15], which has wide application in the multi-view study of features fusion [16]. Yang et al. [17] presents a CCA network (CCANet) to address image classification. This represents images by two-view features. Multi-view study usually treats homogeneous data as its input. However, in this study, we attempt to put the CCA method into heterogeneous data.

Algorithm 2 shows the CCA Algorithm:

Algorithm 2. The canonical correlation analysis (CCA) algorithm.

Input: $\mathsf{\delta }=\{x_i,y_i|\left(x_i\in R^m,y_i\in R^n,i=1,\dots ,K\right)$

Output: $\mathsf{\rho }$—the correlation coefficient of output: X, Y;

Step 1: calculate the variance of X and Y: $S_{xx},S_{yy}$ and covariance of X and Y, and Y and X: $S_{xy}{S}_{yx}$;

Step 2: calculate the matrix $M=\sqrt[2]{S_{xx}}\ast S_{xy}\ast \sqrt[2]{S_{yy}}$;

Step 3: make singular value decomposition for matrix M, obtain the largest singular value $\mathsf{\rho }$ and its corresponding left and right singular vectors $U$ and $V$;

Step 4: calculate the linear coefficient vectors of X and Y: $a=\sqrt[2]{S_{xx}}\ast U,b=\sqrt[2]{S_{yy}}\ast V$;

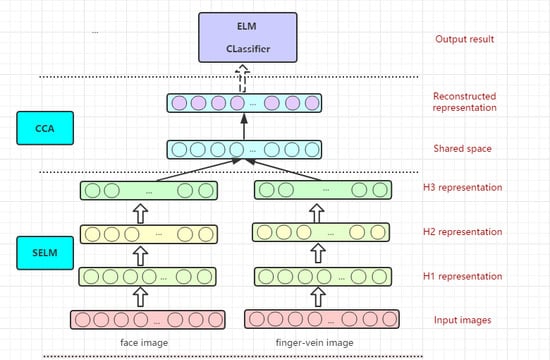
2.2. Proposed Method

This section describes our proposed method, which includes the related theory, structural frame, and algorithm steps:

2.2.1. The Stacked ELM Model

The most important thing in most supervised learning tasks is the effectively learning of the abundant characteristics of data, which represent whether the model has good generalization performance. Limited by the single hidden-layer feed forward neural network architecture, the traditional ELM model is unable to capture a high level of abstraction of accurate information although there are a lot of hidden nodes. Meanwhile, compared with the multilayer neural network, deep architecture can help elucidate the hierarchy of characteristics to construct a high-level presentation of data from low-level characteristics. However, affected on the influence of the BP algorithm, the deep neural network trains slowly and has lower efficiency. To make full use of the advantages of the ELMs and the deep neural network, this study proposes improving learning features by means of unsupervised learning via stacked ELMs and transferring the step-by-step low-level features to form complete feature representation. The model essentially is a multilayer feed-forward network and its parameters are achieved by a cascade of extreme learning machines.

The stacked ELM model can also be disassembled into multiple ELM models, where each hidden layer can be regarded as an independent ELM for feature extraction. Furthermore, to complete the reconstruction of the input, the ELM treats input as the ideal target output (i.e., $T=X$). Figure 1 describes the feature learning process for the stacked ELM model in detail where the input image is treated as the target output in the first ELM ($T=X$) to calculate the output weight matrix ${\beta }_1$ (in red box). Then, the output of the first hidden layer $H_1={\beta }_1\times X$ is treated as the second input and target output of the ELM ($T=H_1$) to calculate the output weight matrix ${\beta }_2$ (in green box). Finally, we obtained a high-level feature representation ${\beta }_3\times H_2$. Hence, the system becomes a linear model and the output weight matrix of each ELM ${\beta }_k$ can be computed according to the number of hidden-layer nodes. By using the recursive learning approach, we get the unsupervised high-level feature representation for original input data—the $h$ hidden-layer output, which is $H_h$.

2.2.2. The S-E-C Model for Multi-Biometrics Recognition

The multimodal deep-learning model can be divided into two categories according to the input data types [18]: homogeneous input data and heterogeneous input data. The homogeneous data conforms to the similar statistical law. Differ from homogeneous data, the heterogeneous input data has a great gap in statistics law, such as in the form of text and image data. When the input of each modality is homogeneous data, we usually cascade the modal data into a vector as input of the deep-learning method, such as Stacked Auto-Encoder (SAE) or Deep Belief Network (DBN), while the Restricted Boltzmann Machines (RBM) or Auto-Encoder (AE) serves as the multimodal input characters. The approach establishes the common model according to the distribution of distinct input data but ignores the particularity of each modality. As a result, it is usually hard to get the optimal joint expression. Meanwhile, for the heterogeneous input data, Ngiam presented a method that trains each modality for the first layer feature expression. This method assumed that the lower hidden-layer realizes a single-mode state expression, while the high-level expression is multimodal. Figure 2 shows the structural frame of the proposed model named the S-E-C model.

The multimodal training system is divided into three separate stages: unsupervised feature representation of each modality, features fusion between the modality, and supervised classification. The multimodal input data are face images and finger-vein images, which belong to heterogeneous data. For feature extraction, we obtain the high-level hidden-layer representation of two modals via stacked ELM (H3 Representation), and for fusion strategy, we selected the CCA method. The application of the CCA method to our model has following advantages: First, the CCA method is similar to the principal component analysis method, which can reduce the feature dimension without losing information and further reduce computing consumption. Second, the CCA method can analyze the correlation between the two groups of variables, which aids in the reconstruction of cross-modal characteristics.

In the previous step of our model, the same method is used for unsupervised feature representation of each modal to obtain a unified expression for further conduction, which presented a symmetric structure in the model.

A detailed description of the S-E-C model is shown as follows:

Given a training set that contains m samples $({\mathrm{x}}_1^{(i)},{\mathrm{x}}_2^{(i)},{\mathrm{l}}^{(i)})(i=1,\cdots ,m)$, here, $x_1^i\in R^{n_c}$ is the face feature vector for ith sample, $x_2^{(i)}\in R^{n_d}$ is the finger-vein feature vector for ith sample, $l^{(i)}\in R^2$ is the corresponding label vector for ith sample $(x_1^{(i)},x_2^{(i)})$, and $n_c,n_d$ denote the dimension of face feature vector and finger-vein feature vector, respectively. The feature vectors of all the m samples constitute a new feature matrix $X_1,X_2$, and the corresponding label matrix is $L$. Algorithm 3 shows the whole training algorithm.

Algorithm 3. The S-E-C algorithm description.

Input: face feature matrix $X_1={[x_1^{(1)},x_1^{(2)},\cdots ,x_1^{(m)}]}^T$, finger-vein face vector $X_2={[x_2^{(1)},x_2^{(2)},\cdots ,x_2^{(m)}]}^T$ and label matrix $L_2={[l_1^{(1)},l_1^{(2)},\cdots ,l_1^{(m)}]}^T$.

Output: weight matrix $W_{i,j}(i\in [1,k],j\in [1,2]),$

Initialize: choose the depth of the model for each modality $k$ and hidden-layer node $n_k$.

for j = 1 to 2 do

$H_{0,j}=X_j$

for i = 1 to k do

(1) Randomly generating hidden-layer input weighting matrix $W_{i,j}$ and Bias matrix $B_{i,j}$;

(2) Calculating hidden-layer output: $H_{i,j}=g(W_{i,j}{H}_{i-1,j}+B_{i,j})$;

(3) Computing ${\hat{\beta }}_{i,j}$ using Equations (3) or (4) under the condition

$H=H_{i,j},T=H_{i-1,j}$;

(4) calculating $W_{i,j}$, $W_{i,j}={\widehat{(\beta }}_{i,j}{)}^T$;

(5) update the hidden-layer output: $H_{i,j}=g(W_{i,j}{H}_{i-1,j}+B_{i,j})$;

end for

end for

Canonical correlation analysis:

(1) Calculate the variance of $H_{k,1}^T$ and $H_{k,2}^T$: $S_{xx}=\mathrm{cov}(H_{k,1},H_{k,1})$, $S_{yy}=\mathrm{cov}(H_{k,2},H_{k,2})$ and $S_{xy}=\mathrm{cov}(H_{k,1},H_{k,2})$

(2) Calculate the matrix M: $M=\sqrt{S_{xx}}\ast S_{xy}\ast \sqrt{S_{yy}}$;

(3) Make singular value decomposition for matrix M, obtain the largest singular value $\mathsf{\rho }$ and its corresponding left and right singular vectors $U$ and $V$: $[U,D,V]=SVD(M)$;

(4) Calculate the linear coefficient vectors of $H_{k,1}^T$, $H_{k,2}^T$: $Z_x=\sqrt{S_{xx}}\ast U,Z_y=\sqrt{S_{yy}}\ast V$;

(5) Construct feature representation: $H_{k+1}=Z_x+Z_y$.

Supervised training and testing:

Applying simple ELM to a new dataset $[L,H_{k+1}]$

Computing ${\hat{\beta }}_{k+1}$ using Equation (3) or (4) under the condition $H=H_{k+1},T=L$:

Figure 2 shows that the face and finger-vein image are treated as the input layer of the S-E-C model and is expressed as follows:

$$H_{0,j}=X_j(j=1,2)$$

(4)

To learn the high-level representation of modal characteristics, we apply a two-layer stacked ELM to face image features $X_1$ and finger-vein image features $X_2$ for feature learning prior to the modal information fusion. The output of the hidden layer can be respectively described as follows:

$$H_{i,j}=g(W_{i,j}{H}_{i-1,j}+B_{i,j}),\mathrm{for}i=1,2,3;j=1,2,$$

(5)

where $g(·)$ is the hidden-layer activation function, with sigmoid function $H_{*}$ (* subscript on behalf of the hidden layer and the modality) is the hidden-layer output matrix, which denotes the nonlinear feature extracted from both the face image feature $X_1$ and the finger-vein image feature $X_2$. For example, $H_{i,j}$ expresses the feature representation of $j\mathrm{th}$ modality and $i\mathrm{th}$ hidden layer. Similarly, $B_{*}$ represents the bias matrix of the corresponding modality and hidden layer.

When getting high-level features within the modal, that is $H_{3,1},H_{3,2}$, we try to obtain the joint feature expression by using the CCA method, which is expressed as follows:

$$H_4=f(H_{3,1},H_{3,2})$$

(6)

where $f(·)$ denotes the CCA fusion method.

Lastly, we will receive two-modal joint characteristic representation $H_4$, and then place it into an ordinary ELM classifier, which studies the relationship between the characteristics and the label, and then try to test new samples:

$$L=g(W_5{H}_4)$$

(7)

3. Results

3.1. Database

3.1.1. The Olivetti Research Laboratory (ORL) Face Dataset

The ORL face dataset was founded by the University of Cambridge, which is composed of 40 people. Figure 3 shows that each person holds 10 photos, having a total of 400 pieces.

3.1.2. The Face Recognition Technology (FERET) Face Dataset

The FERET Face database stems from a facial recognition technology engineering called FERET. This was launched by the United States Department of Defense. It is composed of 200 people where each person has 7 face images for a total of 1400 copies. This is considered the most authoritative face database as shown in Figure 4.

3.1.3. The MMCBNU-6000 Finger-Vein Dataset

The MMCBNU-6000 finger-vein database was performed by Chonbuk National University, which includes 100 people, gathering everyone’s index, middle, and ring finger of both hands. Each finger has 10 images with a total of 6000 images, as shown in Figure 5.

This study selects face images and finger-vein images from the three datasets described above to constitute two hybrid databases, thereby establishing a total of two datasets:

(a)

ORL+MMCBNU: total of 400 groups with each group taking 10 face images and 60 finger-vein images;

(b)

FERET+MMCBNU: total of 1000 groups with each group taking 7 face images and 60 finger-vein images.

3.2. Experimental Environment

The experimental environment is described as follows: Windows 10 operating system with 64-bit, built on ×64 processors which type is Intel Core i7-4770, along with an 8 GB computer memory. The simulation environment used is MATLAB_2016 Ra.

3.3. Experiment Results and Analysis

3.3.1. Ability to Represent Hidden-Layer Features of Stacked ELM

The experiment mainly verifies the ability for data classification using the multilayered neural network to represent image characteristics. Three different datasets were chosen for the experiment (80% of data for training and the rest for testing, with 5-fold cross-validation). We compared three shallow classifiers Back Propagation (BP), Support Vector Machine (SVM), ELM and a classical deep-learning method Convolutional Neural Network (CNN) with our proposed method. The shallow classifier treats image pixel features as input and has parameters as typical values. Furthermore, the CNN model is named lenet-5, which makes twice the convolution and pooling operation on input images, plus a full connection operation to get output. Moreover, we compare the proposed method with other deep-learning methods mentioned in the literature, such as Stacked Auto-Encoder (SAE) [3] and Deep Belief Nets (DBN) [5].

Table 1. Experimental performance for different method on three datasets.

Experiment Methods	ORL		FERET		MMCBNU
	Time (s)	Accuracy	Time (s)	Accuracy	Time (s)	Accuracy
BP	8.2459	88.45%	9.9887	89.96%	12.7864	91.73%
SVM	6.7680	90.32%	8.7869	91.92%	10.3670	93.02%
ELM	1.3786	89.38%	2.0679	90.87%	2.8568	92.62%
CNN (lenet5)	28.8769	92.48%	34.8979	93.06%	45.3478	94.84%
SAE	36.7842	93.64%	42.2985	94.46%	69.3587	95.24%
DBN	30.3478	90.82%	38.8876	92.34%	60.5874	94.48%
Stacked ELM (H3)	10.2714	93.62%	14.3224	94.58%	17.6368	95.58%

shows that the performance of the three shallow methods is almost similar (nearly 90%). Meanwhile, ELM performs better in terms of time (a few times). The deep-learning methods, such as CNN, SAE, and DBN, perform better than the shallow methods (higher than 2%). It proves that deep learning enables learning of higher-level abstract concepts and understanding of semantic information. However, the deep-learning methods bring shortcomings in terms of time because its training time is several times longer than that of the shallow methods. The stacked ELM, as one of the deep-learning methods, also performs better than shallow methods. Moreover, compared with other deep-learning methods, stacked ELM inherits the advantage of ELMs (faster learning speed and no need for fine tuning) and performs better in terms of time. It requires less time than other deep-learning methods, which reveals the powerful learning ability of deep architecture.

3.3.2. Comparison of the Classification Effect of the CCA Fusion Method

This experiment explores the effectiveness of the CCA fusion method. We conducted three groups of experiments. The first experiment takes three different datasets (80% for training, 20% for testing, and also 5-fold cross-validation) to measure performance, which serves as the benchmark for the other two experiments. The second experiment applies the simple cascade fusion strategy to mixed datasets. The third experiment conducted on the same dataset as experiment 2, applied the CCA fusion method to two different biological characteristics, added an ELM classifier, and also tested recognition performance.

Table 2. Multi-biometrics fusion performance.

Biometrics	Performance (Accuracy %)
ORL	89.38%
FERET	89.87%
MMCBNU-6000	92.62%
ORL+MMCBNU (cascade)	93.51%
FERET+MMCBNU (cascade)	93.67%
ORL+MMCBNU (CCA)	94.46%
FERET+MMCBNU (CCA)	94.97%

shows the fusion features (both cascade strategy and CCA method) compared with single modal features. This can improve performance and prove the effectiveness of the fusion method because it takes into consideration more features and obtains a better performance, in theory. Compared with the traditional cascaded fusion features, the CCA method fusion features provide more effectual performance (about 1%), which proves the efficiency of CCA fusion. Moreover, the CCA method reduces the dimension while extracting features, which renders it more accommodating to image recognition performance.

3.3.3. Experiment Performance for Different Methods on Different Hidden-Layer Nodes

This experiment compared the recognition accuracy for different methods on different hidden-layer nodes. The number of hidden-layer nodes is a parameter in using ELM as a classifier. The experiment compares three methods. The first method is a simple ELM which has a single-mode biometric image characteristics input (group 1 is face image, and group 2 is finger-vein image). The second method is also ELM but with multimodal shallow fusion image characteristics (group 3). The third method uses deep neural network (CNN) to extract biological image characteristics with an added ELM classifier. The last method is the proposed one in this study.

Figure 6 shows that as the change of the different hidden-layer nodes, the two kinds of multimodal fusion method can achieve better performance. Compared with other single-mode models, the multiple modal model, which uses two kinds of modal information, obtains a more robust result. Our proposed method and the shallow combination method both integrate multimodal information, but our approach is superior to the other, for in the shallow layer fusion method, the different statistical features are simply mixed, which is only a fusion in the form, and therefore ignores the particularity of information about specific modality.

3.3.4. Effect of Parameters for Recognition Accuracy

For the S-E-C model, the most important parameters are regularized least squares calculation parameters $\lambda$ and the number of hidden-layer nodes $n_h$. Therefore, as shown in Figure 7 and Figure 8, two experiments are conducted to analyze the effect of parameter change on model performance. Figure 7 describes the changing trend of recognition accuracy along with the change of parameter $n_h$, while keeping the fixed parameter $\lambda$. Similarly, Figure 8 describes the changing trend of recognition accuracy along with the change of parameter $\lambda$, while keeping the fixed parameter $n_h$.

The diagram shows that the S-E-C model follows a similar convergence to the ELM method, and its performance keeps mostly stable in an extensive range of the value-space for parameters $\lambda$. Therefore, we can choose the parameters that hold higher test precision as the optimal parameters of the S-E-C model.

4. Discussion

Multimodal biometric fusion is an effective method to improve biometrics performance. This paper presents a new kind of multimodal biometrics recognition network model named the S-E-C model, based on stacked ELM and CCA methods. For the model, high-level special expression of the multimodal biometric image is learned firstly and then carries on the multimodal biometric fusion. Finally, a simple ELM classifier act on the fuse representation to realize multi-modal biological recognition.

In this study, the S-E-C model can make full use of stacked ELMs to extract high-level information. As a kind of artificial neural network, the deep extreme learning machine can obtain the advantages of the ELM and deep-learning methods. This method approximates complex functions and therefore, does not require iteration fine-tuning. Furthermore, this study described the method as stronger, more flexible, and with a higher computational efficiency than other deep-learning methods. Finally, we verify the effectiveness of the general performance of the S-E-C model. The experimental results demonstrate that our method has a significant advantage when compared with several other contemporary algorithms.

This study used the CCA method in multimodal biometric fusion, which obtained different modal correlation of biological characteristics. In the future, we plan to take the ideas of regression into consideration, and try to build another modal biological characteristic by using multimodal biometrics, and finally realize the image retrieval of multimodal biological characteristics.