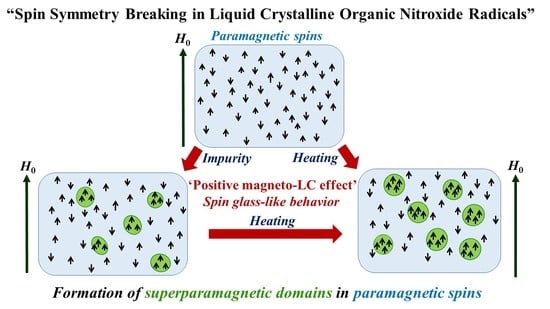
Spin Symmetry Breaking: Superparamagnetic and Spin Glass-Like Behavior Observed in Rod-Like Liquid Crystalline Organic Compounds Contacting Nitroxide Radical Spins

Abstract

Liquid crystalline (LC) organic radicals were expected to show a novel non-linear magnetic response to external magnetic and electric fields due to their coherent collective molecular motion. We have found that a series of chiral and achiral all-organic LC radicals having one or two five-membered cyclic nitroxide radical (PROXYL) units in the core position and, thereby, with a negative dielectric anisotropy exhibit spin glass (SG)-like superparamagnetic features, such as a magnetic hysteresis (referred to as ‘positive magneto-LC effect’), and thermal and impurity effects during a heating and cooling cycle in weak magnetic fields. Furthermore, for the first time, a nonlinear magneto-electric (ME) effect has been detected with respect to one of the LC radicals showing a ferroelectric (chiral Smectic C) phase. The mechanism of the positive magneto-LC effect is proposed and discussed by comparison of our experimental results with the well-known magnetic properties of SG materials and on the basis of the experimental results of a nonlinear ME effect. A recent theoretical study by means of molecular dynamic simulation and density functional theory calculations suggesting the high possibility of conservation of the memory of spin-spin interactions between magnetic moments owing to the ceaseless molecular contacts in the LC and isotropic states is briefly mentioned as well.

1. Introduction

Following the birth and establishment of ‘Einsteinian general theory of relativity’ and ‘quantum theory and mechanics’ at the beginning of the 20th century [1], the ‘complexity theory’ developed rapidly since the 1970s is recognized as one of the paradigm shifts or innovations in science in the same century [2,3,4]. Currently, a concept of the nonlinear and nonequilibrium (or out of equilibrium) complexity theory is known to govern a variety of dynamic behaviors observed in both natural and social sciences [5,6,7,8,9]. In the nonequilibrium complexity system, symmetry breaking takes place easily during transition from a chaotic or dissipative state to another one. The fluctuation in a nonequilibrium state induces a phase transition to trigger the symmetry breaking, and, eventually, the nonlinear amplification of fluctuation leads to dissymmetric circumstances [5,6,7,8,9,10]. The most dramatic and important event is the birth of the universe by the cosmic inflation followed by the Big Bang starting from a quantum fluctuation, according to the ‘uncertainty principle of energy and time’ as a hypothetical explanation [1]. After the selection of ‘matter’ against ‘anti-matter’ resulting from the CP (charge conjugation parity symmetry) violation in the universe, the important and familiar events on the earth include many body interactions of multiple elements responsible for the nonlinearity [11]. The intermolecular interactions can create nonequilibrium objects such as cells [12], bubbles [13], and metastable crystals [14], which may have strong links to the origin of selected chirality of life. Thus, symmetry breaking has been playing a primordial role in physics, chemistry, life science, and so forth.

Liquid crystals, which are defined as a thermal mesophase between crystalline and isotropic phases, and, hence, can be regarded as high-temperature polymorphs of crystals, are unique soft materials that combine anisotropy and fluidity. From a different point of view, liquid crystalline (LC) phases are considered to be a sort of complexity system consisting of nonequilibrium dynamic states due to the molecular motion and the coherent collective properties of molecules in the LC state [8]. Therefore, they are so sensitive to external stimuli, such as electric or magnetic field, heat, light, temperature, pressure, and added chiral dopants, that the LC superstructure can easily be altered and the change can be controlled [15,16]. In this context, it seems challenging and promising to develop organic soft materials that can show a novel complexity phenomenon in response to various external stimuli by making use of the LC environment.

In this connection, magnetic LC compounds had attracted great interest as soft materials to enhance the effect of magnetic fields on the electric and optical properties of liquid crystals. They were anticipated to exhibit unique magnetic interactions and, thereby, unconventional magneto-electric [17,18,19,20] or magneto-optical properties in the LC state [21,22,23]. However, there had been no prominent study on these interesting subjects in the 20th century because the majority of magnetic liquid crystals examined were of a highly viscous transition (d-block or f-block) metal-containing metallomesogens (Figure 1) [24,25], which were not suitable for investigation of the swift molecular motion and reorientation in the LC phases at moderate temperatures in weak magnetic fields. At present, no appreciable intermolecular ferromagnetic or superparamagnetic interaction (in other words, spin symmetry breaking) has been observed in the LC state of d-block or f-block metallomesogens.

Only a few all-organic LC radical compounds were prepared until 2003 because it was believed that the geometry and bulkiness of the radical-stabilizing substituents were detrimental to the stability of liquid crystals, which requires molecular linearity or planarity [25,26,27]. Although several rod-like organic LC compounds with a stable cyclic nitroxide unit as the spin source were prepared (Figure 2), their molecular structures were limited to those containing a nitroxyl group in the terminal alkyl chain, away from the rigid core, and, thereby, allowed the free rotation of the nitroxyl moiety inside the molecule, resulting in a very small dielectric anisotropy (∆ε) of the whole molecule [25,26,27].

With this situation in mind, since 2004, we have designed and synthesized a series of chiral and achiral all-organic LC nitroxide radicals such as 1–5 having one or two PROXYL (2,2,5,5-tetrassubstituted-1-pyrrolidinyloxyl) units in the core position and, thereby, with a negative dielectric anisotropy (∆ε < 0) (Figure 3) [28,29,30,31,32,33,34,35,36,37,38,39,40,41,42,43,44]. Their LC phases and magnetic properties have been fully characterized. Consequently, we could observe a magnetic hysteretic behavior between the heating and cooling processes for all of these LC compounds by a SQUID magnetic susceptibility measurement. The molar magnetic susceptibility (χ_M) always increased at the crystal-to-LC phase transition and this χ_M increase was always preserved during the cooling process. This unique magnetic hysteretic behavior was referred to as a ‘positive magneto-LC effect’ [34,35,36]. Measurement of the magnetic field (H) dependence of molar magnetization (M) indicates that the observed magnetic hysteresis corresponds to the emergence of superparamagnetic behavior, that is, the partial formation of ferromagnetic domains in the LC phases. These experimental results were contrary to the general knowledge that the possibility of a ferromagnetic LC material had been considered unrealistic due to the inaccessibility of long-range spin-spin interactions between rotating molecules in the LC state at ambient or higher temperatures [26]. However, since the positive magneto-LC effect is observed only for specific PROXYL radicals showing an LC phase (Figure 3), it is suggested that the breaking of time reversal symmetry of radical spins is likely to have a strong connection with the partially broken space symmetry of LC phases of these compounds. Thus, the observed magnetic behavior reminds us of a spin glass state. In fact, for example, considerable enhancement of a positive magneto-LC effect or superparamagnetic behavior was noted by adding a small amount (5 to 20 mol%) of racemic cis-diastereomers (R*,R*)-3 [a 1:1 mixture of (R,R)-3 and (S,S)-3] to meso (R,S)-3 as an organic impurity [42]. Such thermal and impurity effects are known to be commonly observed for metallic spin glass materials.

Here, it should be emphasized that the positive magneto-LC effect (χ_M increase) (i) proved to be independent of the magnetic field-induced molecular reorientation because of the too small molecular magnetic anisotropy (∆χ) [45] and (ii) did not result from the contamination by extrinsic magnetic metal or metal ion impurities, as confirmed by the quantitative analysis using inductively coupled plasma atomic emission spectroscopy (ICP-AES) as well as the observation of thermal and impurity effects [42].

Thus far, there have been two theoretical studies to contribute to the elucidation of the mechanism of positive magneto-LC effect. By the quantitative analysis of angular dependence of g-values and ∆H_pp (line-width) of EPR spectra and DFT calculations of spin density distribution in the interacting molecules based on the crystal structure of an analogous compound, Vorobiev et al. revealed that an intermolecular spin polarization mechanism operating between neighboring radical molecules rather than the direct through-space interactions between the paramagnetic centers contributes to the occurrence of the positive magneto-LC effect [46]. Furthermore, quite recently, by means of molecular dynamic (MD) simulation and density functional theory (DFT) calculations, Uchida et al. has revealed that the positive magneto-LC effect can originate from the conservation of the memory of spin-spin interactions between magnetic moments, owing to the ceaseless molecular contacts in the LC and isotropic states. They incorporated the molecular mobility effects [44] into the quantitative Thouless-Anderson-Palmer approach, which was proposed to solve the Edwards-Anderson model for spin-glasses with inhomogeneous magnetic interactions [47].

In addition, it is noteworthy that the nonlinear magneto-electric (ME) effect was, for the first time, detected for organic LC materials, i.e., (S,S)-1 (m = n = 13) showing a ferroelectric LC [chiral SmC (SmC*)] phase [37,38,39]. By applying an external DC electric field (between +25 V and −25 V) to the (S,S)-1 confined in a rubbed surface-stabilized liquid-crystal thin (4 μm thick) sandwich cell, the hysteresis loops were observed for the experimental EPR parameters such as the g-value, ∆H_pp, and χ_rel (relative paramagnetic susceptibility). These experimental results suggest that the interactions between the electric polarization and the magnetic moment in the magnetic LC phase are likely to contribute to the enhancement of a positive magneto-LC effect in weak magnetic fields. In fact, the highly enantiomerically-enriched compounds (S,S)-1 always exhibited a larger positive magneto-LC effect than the corresponding racemic ones trans-1 [35,36].

Due to the latest comprehensive review as well as database-like article regarding the preparation, characterization, and magnetic properties of a wide array of all-organic LC radicals synthesized, thus, far, an excellent one entitled “Liquid crystalline derivatives of heterocyclic radicals” by Kaszyński is strongly recommended to refer to Reference [27].

In Section 2, the fundamentals of super-para-magnetism are briefly mentioned. In Section 3, the typical properties of canonical spin glasses composed of diluted magnetic alloys and the non-canonical spin glass-like behavior of the other systems are summarized. In Section 4, the selected important experimental results featuring the magnetic properties of positive magneto-LC effect observed for LC nitroxide radical compounds are summarized. In Section 5, the mechanism of positive magneto-LC effect is proposed and discussed on the basis of the magnetism of the spin glass state and the ME effect.

2. Super-Para-Magnetism

Super-para-magnetism is a paramagnetic behavior of magnetic domains or clusters. The collective magnetic spins in a domain are aligned parallel to the external magnetic field, and there is no remanent magnetization of the sample, similarly to paramagnets. However, the spins are ferromagnetically-ordered inside each domain. To behave like paramagnets, domains of ferromagnetically-ordered moments should readily respond to the applied field (Figure 4). Such a situation can be realized in domains with a rotational degree of freedom or domains with a sufficiently low energy barrier of magnetic anisotropy (i.e., coercive force).

The net magnetization of super-para-magnets are expressed by the equation below.

$$M=N\mu L\left(\mu \right)=N\mu \times \left(\coth \frac{\mu H}{k_{B}T}-\frac{k_{B}T}{\mu H}\right)$$

(1)

$N$ denotes a number of domains, $\mu$ does the magnetization summed in a domain, and $k_B$ is the Boltzmann factor. $L\left(\mu \right)$ is called Langevin function. In the case that there is distribution in $\mu$, the net magnetization should be estimated by integration over the distribution function $P\left(\mu \right)$ [48].

Here, it is worth noting that the size effect of the domain is a very important factor, since the anisotropic energy in a domain is expressed by the product of the anisotropic coefficient (K) and volume size (V) of the domain. The $V$ value, which satisfies $KV<T,$ makes the magnetic moments paramagnetic. As the $V$ becomes larger, the anisotropic energy of a domain also increases so that it turns to the coercive force at $KV>T$.

3. Spin Glass

3.1. What Is a Spin Glass?—General Experimental Features

Spin glass (SG) is a frozen state of spins without long-range periodicity [49]. In the SG, although the long-time average of spins at each site has a non-zero value as seen in a conventional, magnetically-ordered state, both the magnitude and direction are random at each site (Figure 5). The name SG comes from the glass transition in which the atomic positions take random values.

If the SG state is expressed in a thermodynamic way with a spin (S_i) of the i-th site, the local spontaneous magnetization (m_i) has a non-zero value (Equation (2)), even though the site averaged value (m) is zero (Equation (3)).

$$m_i=⟨S_i⟩\ne 0$$

(2)

$$m=\frac{1}{N}{\displaystyle \sum }_i^N{m}_i=0$$

(3)

Here, $N$ denotes the total number of spins. To distinguish the SG state from a paramagnetic state or a long range ordered state, the combination of $m$ and the second order moment (q) with respect to the thermal average of $S_i$ is often used (Equation (4)).

$$q=\frac{1}{N}{\displaystyle \sum }_i^N⟨S_i{}^2⟩\ne 0$$

(4)

Historically, the first SG state was found in dilute magnetic alloys such as AuFe and CuMn [50,51]. Such systems are called canonical SGs, which are the most studied and established system in the SG theory. Canonical SGs consist of a random distribution of local magnetic impurities in nonmagnetic metal hosts. The features in which canonical SGs show experimentally can be summarized as follows.

• Hysteresis: The emergence of hysteresis of magnetic susceptibility (χ) under a different temperature control process (Figure 6 [51]).
• Impurity effect: Non-linear or non-monotonic increase of χ with the increment of an amount of the magnetic impurity (Figure 6 [51]).
• Long-time scale dynamics.
• AC magnetic susceptibility sensitive to the frequency of the external magnetic fields near the spin freezing temperature.
• A broad peak in magnetic specific heat around the spin freezing temperature.

The features 1–3 observed for LC nitroxide radicals are described in Section 4. For feature 4, we do not discuss it because of the difficulty in the measurement of AC magnetic susceptibility for LC nitroxide radicals at high temperatures. Likewise, we cannot discuss the feature 5 concerning the LC nitroxide radicals at high temperatures because the contribution by molecular motion is dominant in the specific heat data for these compounds.

3.2. Theoretical Key Ingredients in Canonical SGs

The key ingredients in canonical SGs are considered to be randomness, frustration, and competing interactions, which are fully equipped in dilute magnetic alloys [52]. A magnetic moment interacts with other moments by means of Ruderman-Kittel-Kasuya-Yoshida (RKKY) interactions via the conductive electron. The RKKY interactions are expressed as shown in Equation (5).

$$J_{ij} ~ \frac{\cos \left(2k_F{r}_{ij}\right)}{r_{ij}{}^3}$$

(5)

where $k_F$ denotes the Fermi energy of the hosting metal and $r_{ij}$ is the distance between two magnetic moments at $i$ and $j$ sites. Since $\cos \left(2k_F{r}_{ij}\right)$ is an oscillating function of $r_{ij}$, $J_{ij}$ can have various plus and minus values as a function of $r_{ij}$.

The random distribution of magnetic impurities then results in random magnetic interactions between each impurity site. Under such a network of irregular interactions, some of these local sites are likely to undergo competition of interactions and be unable to settle down in a certain spin state, which satisfies the energy minimum for each interaction. Such a situation is called frustration.

The combination of randomness and frustration gives many stable states in the local energy, so that it would bring the manifold metastable states in the whole system. Accordingly, the free energy (F) of the SG states has many local minima (Figure 7) and this is called a multi-valley structure. This characteristic structure inherent in SGs results in various features listed in Section 3.1.

3.3. Character of the Magnetism

3.3.1. Hysteresis

The hysteresis results from the multiple metastable states permitted in the material, whereas an ordinary long range ordered state has a unique ground state. As shown in Figure 6, the hysteresis in magnetic susceptibility is most noticeable when the material is cooled below the SG transition temperature ($T_{\mathrm{SG}}$) from the paramagnetic phase. If the sample is cooled in the absence of external magnetic field [this is called ‘zero field cooling’ (ZFC)], the net magnetization of the sample generally does not have a large value. This is observed as a cusp near the spin freezing temperature. On the other hand, if the material is cooled in the presence of a non-zero external field [this process is called ‘field cooling’ (FC)], some of the spins, but not all of them, would align with the magnetic field leading to a ferromagnetic behavior. Thus, in the SG phases, the magnetization after the FC process is larger than that after the ZFC process.

3.3.2. Impurity Effect

In canonical SGs, the concentration (x) of magnetic impurities in nonmagnetic metal hosts has considerable effects on its magnetic property. In a wider range of x values, each SG state takes one of various ground states. Figure 8 shows a schematic for the relationship between the x values and the resulting magnetic properties. At the low limit of x value, dilute magnetic impurities can be regarded as isolated spins, so that the Kondo effect would work between the conducting electron spins and the isolated spins (Figure 8a). A pair of conducting electron spin and isolated spin adopts a singlet ground state to vanish the susceptibility at low temperatures. With the increasing x value, the average impurity-to-impurity distance becomes shorter enough to induce RKKY interactions, forming an SG state (Figure 8b). When the x value exceeds ~10 at.%, some of the impurities exist in the nearest neighbor lattice points so that such locally high-concentrated spin clusters result in the coexistence of the SG state and ferro-magnetic or anti-ferro-magnetic domains (Figure 8c). These clusters are most likely to behave like super-para-magnets, and also exhibit a hysteresis in the temperature dependent of magnetic susceptibility, as a sort of SG behavior of the clusters. Such behavior is often called a ‘cluster glass.’ A further increase in the x value makes the ferro-magnetic or anti-ferro-magnetic domains larger, finally, giving an almost ordered state (Figure 8d).

3.3.3. Long Time Scale Dynamics

Long time scale dynamics is another characteristic aspect of canonical SGs. Since there are many metastable states, hopping over the energetic barrier to other states is possible. Such metastable states are realized by a rapid change in external stimuli such as temperature or magnetic field around the SG phase transition. Rapid cooling from the temperature above $T_{\mathrm{SG}}$ to that below $T_{\mathrm{SG}}$ compels the system to take a certain metastable state without immediate relaxing to the lowest energy. The relaxation to the lowest energy state is called the ‘aging phenomenon,’ which takes a typical time of the order of 10²~10⁴ s or more. Thus, the aging phenomenon can be followed by statistical DC magnetization measurements. For example, after keeping the SG state at a high temperature region in the SG phase under the ZFC conditions, the magnetization at the same temperature gradually increases with the elapse of time by applying an external magnetic field (Figure 9) [53]. After a sufficiently long time, the magnetization gets close to the value, which is observed after the FC process.

3.4. Non-Canonical SG-Like Behavior

Besides canonical SG alloy systems, some of the magnetic features summarized in Section 3.1 are observed in a variety of magnetic systems, which are often called ‘SG-like behavior’ [52]. The features can show up even if some of the key ingredients (i.e., randomness, frustration, and competing interactions) are weak or missed in the systems. In general, neither the diluted conditions of spins nor RKKY interactions are needed for the realization of SG-like behavior. The SG-like behavior is reported in many non-diluted magnets with exchange/super-exchange interactions between the nearest neighbor spins. It seems that the SG-like behavior tends to arise if only there exist some factors of randomness and/or inhomogeneity in the interaction network. They have been often found in atom-doped/substituted systems, grain boundary, systems with site-mixing or random local distortion, and more [52].

4. Positive Magneto-LC Effect

Here, the unique magnetism of LC nitroxide radicals, which is regarded as SG-like behavior, is described. Although the solid-state picture of usual SG-like magnets is not straightforwardly applied to the liquid crystal systems, we actually observed the SG-like features 1–3 (hysteresis, impurity effect, and long-time scale dynamics) listed in Section 3.1. In Section 4.1, our discovery of the positive magneto-LC effect, which refers to a magnetic hysteresis (i.e., thermal effect) associated with the emergence of superparamagnetic behavior in the LC state, is demonstrated. The substantial enhancement of superparamagnetic behavior by impurity effect or controlling the magnetic inhomogeneity is mentioned in Section 4.2. An example of long-time scale dynamics is presented in Section 4.1.3. In Section 4.3, the ME effect observed for the first time in the ferroelectric LC phase of the LC nitroxide radical is explained in detail.

4.1. Magnetic Hysteresis by a Thermal Effect

4.1.1. Monoradical trans-1

In 2008, for the first time, we observed a magnetic hysteresis for nitroxide monoradical (S,S)-1 (m = n = 13) showing enantiotropic (reversible) SmC* and N* phases (Figure 3) by SQUID magnetic suscetibiliy measurement (Figure 10a) [34,35]. In the first heating process from the initial crystalline phase, the molar magnetic susceptibility (χ_M) increased at the crystal–to-SmC* phase transition. An additional χ_M increase was noted at the SmC*-to-N* and N*-to-isotropic phase transitions. Interestingly, the overall 12% χ_M increase at the phase transitions in the heating process was preserved during the cooling one from the isotropic phase and even in the second heating one, and the χ_M in the first cooling and second heating processes never followed the curve drawn in the first heating process. Such magnetic hysteretic behavior, an unusual χ_M increase at the crystal–to-LC phase transition in the first heating process, was referred to as ‘positive magneto-LC effect,’ which was observed for all of the LC nitroxide radical compounds 1~5 with full reproducibility. Therefore, the χ_M in the first cooling process are expressed by the equation below.

$${\chi }_{\mathrm{M}}={\chi }_{\mathrm{para}}+{\chi }_{\mathrm{TIM}}+{\chi }_{\mathrm{dia}}$$

(6)

where ${\chi }_{\mathrm{para}}$ represents the paramagnetic susceptibility of radical spins, which follows the Curie-Weiss law (Equation (7)). The $C$ and $\theta$ are Curie constant and Weiss temperature, respectively. For the mono-radical nitroxide compounds examined, the values of $C$ were close to 0.375 corresponding to the S = 1/2 system.

$${\chi }_{\mathrm{para}}=\frac{C}{T-\theta }$$

(7)

The χ_TIM indicates the temperature-independent magnetic susceptibility corresponding to the χ_M increase at the crystal-to-LC phase transition, while the χ_dia represents the temperature-independent diamagnetic susceptibility, which arises from the orbital current and can be calculated using Pascal’s constant for each atom and bond. Since the sum of χ_TIM and χ_dia can be experimentally obtained as the temperature-independent component by χ_M-T⁻¹ plots, according to Equations (6) and (7), the χ_TIM value can be derived.

We observed a nonlinear relationship between the applied magnetic field (H) and the observed magnetization (M) in the chiral and achiral LC phases of trans-1 (m = n = 13) by SQUID magnetometry (Figure 10d). Unlike the Brillouin function, which ordinary paramagnetic radical compounds display, a steep increase was observed at low magnetic fields (~0.1 T) and an oblique linear response was noted at higher magnetic fields. This result implied the emergence of superparamagnetic behavior in the LC phase.

Such spin glass (SG)-like hysteretic or superparamagnetic behavior was also seen for the other LC nitroxide radicals listed in Figure 3. In contrast, non-LC trans-1 analogues bearing much shorter alkyl chains failed to show the magnetic hysteresis because of their common paramagnetic properties. It is worth noting that, with respect to LC trans-1 and the LC derivatives, enantiomerically-enriched samples always exhibited a larger positive magneto-LC-effect (or magnetic hysteresis) at the crystal-to-LC phase transition than the corresponding racemic samples [35,36]. Thus, the positive magneto-LC effect is a unique property inherent in these LC nitroxide radicals, which suggested some relationship between the spatial symmetry of LC phases and the positive magneto-LC effect.

Here, we should stress that such a magnetic hysteresis or superparamagnetic behavior did not result from the magnetic field-induced molecular reorientation in the LC and isotropic phases. The contribution of overall magnetic anisotropy (∆χ) is, at most, ~10⁻⁵ emu/mol [26], while the observed χ_M increases at the crystal-to-LC phase transition points amount to much more than 10⁻⁴ emu/mol in various LC nitroxide radicals. It is also important to examine the possibility of contamination by ferromagnetically-ordered metal or metal ion spins for such nonlinear magnetization curves [54]. Consequently, we could exclude this possibility by the quantitative analysis using inductively coupled plasma–atomic emission spectroscopy (ICP-AES), verifying 0.5~1.3 ppm for the iron content and 0.3~0.6 ppm for the nickel content for LC nitroxide radicals [42]. These values are less than one-tenth of the observed χ_M increase for the individual compounds. Furthermore, these two possibilities (molecular reorientation and contamination) were ruled out by observing a large ‘impurity effect’ explained in Section 4.2.

The measurements of the AC magnetic susceptibilities are necessary to investigate the long time-scale spin dynamics of super-para-magnetic components in LC nitroxide radicals. However, we could not obtain these data due to the difficulties with the measurement at high temperatures. This is our future subject.

4.1.2. Biradical (S,S,S,S)-2

In order to investigate the relationship between the positive magnet-LC effect and the number of spins, we prepared the biradical (S,S,S,S)-2 (>99% ee) showing an enantiotropic chiral nematic (N*) phase (Figure 3) in which the two radical spins do not interact. The χ_M increase at the crystal-to-LC phase transition in the first heating process was $0.8\times {10}^{-3}$ emu/mol (38%) (Figure 11), which was slightly larger than those of LC mono-radicals such as (S,S)-1. This χ_M increase was maintained during the cooling process, similarly to the case of (S,S)-1.

4.1.3. Diradical (R,S)-3

The non-π-delocalized achiral meso diradical (R,S)-3 (Figure 3) showed an enantiotropic hexagonal columnar (Col_h) phase in which each disc was composed of a hydrogen-bonded molecular trimer (Figure 12) [42]. This compound displayed both thermal and impurity effects. Here, only the thermal effect is stated and the impurity effect is described in Section 4.2.

Measurement of the temperature dependence of χ_M for the pure (R,S)-3 indicated that (i) intramolecular anti-ferro-magnetic interactions with a singlet ground state between the two spins dominated below 100 K and (ii) the Curie-Weiss fitting could be implemented between 100 and 250 K to give the average θ value of nearly zero (Figure 13). Although the pure (R,S)-3 showed neither the χ_M increase nor the superparamagnetic M-H behavior in the first heating process at 0.05 T, distinct χ_M increase and superparamagnetic M-H behavior were observed in the first cooling from the isotropic phase and in the second heating run at 0.05 T.

Next, to learn whether a helical columnar structure can be formed in the Col_h phase of achiral (R,S)-3, the temperature-resolved second harmonic generation (TR-SHG) microscopy was performed with an excitation wavelength of 1200 nm and SHG emission at 600 nm in the presence of a magnetic field (<0.5 T) (Figure 14). We observed a weak SHG emission from the surface of the initial crystal phase at room temperature. On the other hand, when the solid sample was heated to 90 °C and the resulting Col_h phase was annealed at the same temperature, the SHG intensity increased with an elapse of time over 10 min. This observation indicates a gradual growth of domains with an inversion symmetry broken state in a magnetic field. The growth of this domain structure with broken inversion symmetry is assumed to be responsible for the generation of a positive magneto-LC effect, since this is quite analogous to the long-time relaxation in a magnetic field observed for the SG state.

4.1.4. Monoradical trans-4

The non-π-delocalized racemic trans-4 and (R,R)-4 (Figure 3), which formed intermolecular hydrogen bonds between the NO and OH groups in the condensed phase displayed an enantiotropic Col_h phase at room temperature and formed LC glasses at lower temperatures. The SQUID magnetometry revealed that the positive magneto-LC effect was gradually increased through the LC glass-to-LC-to-Iso phase transition sequence in the first heating process at both 0.05 and 0.5 T (Figure 15) [44]. This result suggests that molecular mobility is one of the origins of the positive magneto-LC effect, which is consistent with the conclusions by means of MD simulation and DFT calculations so that the positive magneto-LC effect can originate from the conservation of the memory of spin-spin interactions between magnetic moments owing to the ceaseless molecular contacts (Figure 16) [47].

4.2. Impurity Effect—Diradical (R,S)-3

It was the discovery of an impurity effect that was required to demonstrate the similarity of the positive magneto-LC effect to the emergence of superparamagnetic domains in the SG state. We implemented the χ_M-T measurement for two samples with different ratios (80:20 and 95:5) of (R,S)-3 and racemic cis-diastereomers (R*,R*)-3 (Figure 3) [42]. These mixed samples could still show an Col_h phase. However, pure (R*,R*)-3 and the sample with a ratio of 50:50 displayed no LC phase. As shown in Figure 17, appreciable and substantial χ_M increases were noted during the crystal-to-Col_h-to-Iso phase transition sequence for the samples with the ratios of 95:5 and 80:20, respectively. The χ_M increase was $1\times {10}^{-3}$ emu/mol for the former sample and $5\times {10}^{-3}$ emu/mol for the latter one. As shown in Figure 13, the hysteresis was not observed for pure (R,S)-3 within the experimental error limits in the first heating process. In other words, the content of superparamagnetic domains increased by adding (R*,R*)-3 to (R,S)-3 as an organic impurity. Furthermore, this organic impurity effect convinced us that the positive magneto-LC effect is intrinsic in LC nitroxide radicals listed in Figure 3 because the addition of diastereomers would not change the total amount of contaminating magnetic metal ions, if any.

As shown in Figure 18, the H dependence of the superparamagnetic component extracted from the M-H plots for the mixed sample of (R,S)-3 and (R*,R*)-3 (80:20) was well fitted by Langevin function (Equation (1)), indicating the positive magneto-LC effect that originates from the generation of superparamagnetic domains in the LC phase. The amount of super-para-magnetic domains was enhanced compared to the one in the pure sample of (R,S)-3 shown in Figure 13 h.

Thus, the origin of such unique magnetic properties observed in the LC and isotropic phases of achiral (R,S)-3 in the absence or presence of the racemic diastereomers (R*,R*)-3 as the impurity can be rationalized mesoscopically in terms of (i) the preferential formation of SG-like inhomogeneous magnetic domains consisting of super-para-magnetic domains surrounded by para-magnetic spins in the LC phase, (ii) the gradual growth of the size and/or number of super-para-magnetic domains by thermal processing, and (iii) preservation of the overall increased super-para-magnetic domains in the solid phase by cooling until cryogenic temperatures, in weak magnetic fields (<0.1 T) (Figure 19).

4.3. Magneto-Electric (ME) Effect

The magneto-electric (ME) effect had been observed only for inorganic multiferroic materials such as YMnO₃, TbMnO₃, and so forth, which showed both ferroelectric and magnetic order (ferromagnetism or anti-ferromagnetism) at cryogenic temperatures [17,18,19,20].

In this context, it was expected that a unique ME effect might occur in the second-harmonic-generation (SHG)-active [55] and ferroelectric LC (SmC*) phase of the (S,S)-1 (m = n = 13), which displayed both an excellent ferroelectricity [P_S = 24 nC/cm², τ_10-90 = 213 μs, θ = 29°, η = 73.0 m Pa s at 74 °C by the triangle wave method] in a rubbed surface-stabilized liquid-crystal sandwich cell (4 μm thick) [29] and a positive magneto-LC effect (super-para-magnetic interactions) in the bulk SmC* phase [35]. Such an assumption was the case. The temperature dependences of relative paramagnetic susceptibility (χ_rel), g-value, and ∆H_pp were measured by EPR spectroscopy using the thin sandwich cell into which the most appropriate sample of (S,S)-1 (m = n = 13, 65% ee) was loaded (Figure 20).

Since the magnetization measurement of the sample in the LC cell by SQUID magnetometry was technically difficult, χ_para was derived from the Bloch equation (Equation (8)) [56] by using the EPR parameters, such as g, ∆H_pp, and maximum peak height (I′m and −I′m) as described earlier [35,36],

$${\chi }_{\mathrm{para}}=2{\mu }_{\mathrm{B}}g{I^{\prime }}_{\mathrm{m}}∆{H^2}_{\mathrm{pp}}/\left(\sqrt{3}h\nu H_1\right)$$

(8)

where μ_B is the Bohr magneton, h is Planck’s constant, ν is the frequency of the absorbed electromagnetic wave, and H₁ is the amplitude of the oscillating magnetic field. The relative paramagnetic susceptibility (χ_rel,T) in the absence of an electric field is defined as:

χ_rel,T = χ_para/χ₀

(9)

where χ₀ is the standard paramagnetic susceptibility at 30 °C in the heating process. First, the generation of positive magneto-LC effect and ferroelectric switching in the liquid crystal cell was confirmed. By measuring the temperature dependence of χ_rel,T under the conditions in which the applied magnetic field was parallel (Configuration A) and perpendicular (Configuration B) to the cell surface and the rubbing direction in the absence of an electric field, considerable χ_rel,T increases (ca. 40%) together with large ∆H_pp ones, which were noted at the crystal-to-LC phase transition in both cases (Figure 21). The ferroelectric switching at 25 V was verified by polarized optical microscopy in the absence of a magnetic field. The bright fan-shaped texture at −25 V and the dark one at +25 V were distinctly observed [37].

The difference in temperature dependence of g-values along two direction shows that the magnetic susceptibility of the (S,S)-1 clearly has an anisotropy with respect to the molecular axis. Since the Curie constant revealed S = 1/2 nature of the system, the anisotropy stems from high-order perturbation term of exchange interactions with respect to spin-orbit interactions, such as Dzyaloshinkii-Moriya (DM) interactions. Moreover, the temperature dependence in the case of Configuration A (Figure 21c) shows anomalies in the vicinity of ferroelectric LC (FLC) transition. That implies some changes in magnetism in connection with ferroelectricity, while little anomaly was found in the case of configuration B (Figure 21f).

On the other hand, the relative paramagnetic susceptibility (χ_rel,E) in the presence of an electric field is defined as:

χ_rel,E = χ_para/χ₁

(10)

where χ₁ is the standard paramagnetic susceptibility at the initial potential of +25 V and at 75 °C. Next, the electric field dependences of χ_rel,E, ∆H_pp, and g-value were plotted for the (S,S)-1 (m = n = 13, 65% ee), displaying each hysteresis between +25 V and −25 V when the magnetic field was applied only perpendicularly to the electric field and parallel to the rubbing direction (Figure 22).

It is considered that the molecules with the spontaneous electric polarization is inversed by sweeping the external electric field. Therefore, it is noteworthy that the spin inversion accompanies the inversion of the molecule, which can be regarded as a nonlinear ME effect. Since the usual paramagnetic components cannot show such a nonlinear hysteresis loop, the hysteresis indicates the spin flipping of superparamagnetic domains. This result clearly shows the predominance of the electric field over a magnetic field in controlling the super-para-magnetic behavior, since the spin flipping by the electric field occurs even under a large magnetic field of 0.33 T with a constant direction used for this EPR measurement. The direction-of-magnetic field dependence of the g-value, χ_rel,E, and ∆H_pp indicates that the super-para-magnetic domains are directed almost perpendicularly to the spontaneous electric polarization. For both the nonlinear ME effect and the direction-of-magnetic field dependence, the high-order perturbation term of exchange interactions with respect to spin-orbit interactions is usually necessary for this S = 1/2 system.

In summary of Section 4, the unique magnetic properties observed for LC nitroxide radicals are characterized in connection with SG-like magnetic features (see Section 3.1) as follows:

• The hysteresis observed by measurement of the temperature dependence of magnetic susceptibility (Figure 10a, Figure 11 and Figure 13) corresponds to the emergence of superparamagnetic domains in the LC and isotropic phases.
• The superparamagnetic domains grow in the LC phases under external magnetic fields with the elapse of time in minutes (Figure 14 and Figure 15).
• The superparamagnetic components considerably grow with the increasing impurity content or inhomogeneity (Figure 17).

As shown in Figure 18 and Figure 19, these results imply the formation of the super-para-magnetic domains, most likely due to the local inhomogeneity in LC phases. Therefore, this picture is analogous to the cluster glass (See Section 3.3.2), or super-para-magnetic system without magnetic interactions. A partially broken degree of freedom in LC phases is considered to affect the magnetic properties of the domains. The super-para-magnetic response to the external magnetic field is due to the domains’ rotational degree of freedom. Likewise, the factors of molecular mobility and intermolecular interactions resulting in a favorable molecular correlation in LC phases are likely to contribute to the long-time scale growth of superparamagnetic domains. To comprehend the microscopic state of the superparamagnetic domains, we have to investigate the dynamics and interactions between the domains.

Elucidation of the microscopic mechanism for the formation of super-para-magnetic domains in the LC nitroxide radicals is a challenging subject. In this context, we discovered that the nonlinear ME effect occurs in the LC nitroxide radicals (Figure 22). Namely, the super-para-magnetic domains turned out to be controllable by external electric fields. This result demonstrates the ferroelectric aspects of super-para-magnetic domains. Accordingly, in Section 5, we propose and discuss the mechanism of the positive magneto-LC effect on the basis of the nonlinear ME effect.

Meanwhile, quite recently another mechanism has been suggested, in which the positive magneto-LC effect can be accounted for microscopically in terms of the molecular mobility and the resulting inhomogeneity of intermolecular interactions without assuming the formation of superparamagnetic domains by means of MD simulation and DFT calculations (Figure 16) [47]. Namely, the magnetic features seem to reflect the macroscopic inhomogeneity of the liquid crystal orientation field, even though the magnetic properties look like those resulting from the superparamagnetic domains. Since the macroscopic studies on this mechanism is under investigation, only the former mechanism based on the ME effect is discussed in Section 5.

In addition, it is fairly possible that both mechanisms operate complementarily. The latter mechanism originating from the molecular mobility is predominant in the LC and isotropic phases, while the formation of super-para-magnetic domains by the former mechanism results in the preservation of χ_TIM in the supercooled LC and solid phases during the cooling process.

5. Proposed Mechanism

The existence of superparamagnetic domains in rod-like LC nitroxide radicals means the ferromagnetic spin arrangement inside the domains. However, ferromagnetic ordering through the direct exchange interactions between radical spins at ambient or higher temperatures in metal-free organic radicals had been believed to be unrealistic. Moreover, the molecular rotation of as fast as around 10¹⁰ s⁻¹ in a rod-like LC phase may also make the average magnetic interactions much weaker than in a crystalline phase [25,26]. Contrary to such general believing, the positive magneto-LC effect has been observed in the rod-like LC nitroxide radicals with a specific molecular structure, but not in the homologous non-LC nitroxide radicals.

Here, we propose the parasitic ferromagnetism [57] in terms of the nonlinear ME effect, that is, the induction of ferromagnetism by the emergence of the domains with spontaneous electric polarization (Figure 23). If there is a cross-correlation term between magnetization (M) and electric polarization (P) in the free energy, it is plausible that the emergence of M can lower the free energy of the system in the presence of P.

For the operation of this mechanism, the existence of spontaneous polarization (Ps) is necessary, which emerges as the result of breaking the space inversion symmetry. As described in Section 4.3, the Ps is already present in the LC phases composed of chiral nitroxide radical molecules. We could obtain the following three experimental results that indicated the correlation of super-para-magnetic behavior and the breaking of space inversion symmetry. Firstly, the super-para-magnetic domains grow during the crystal-to-LC-to-Iso phase transition sequence in the heating process, in which the birth and growth of domains without space inversion symmetry was revealed by the gradual increase in the SHG signal (Figure 14). Second, the result that the super-para-magnetic domains augmented with the increasing ee value of the LC compounds (See Section 4.1.1) is likely to demonstrate the correlation of the positive magneto-LC effect and the breaking of space inversion symmetry. Third, and more importantly, it was the external electric field that flipped the g-value of the EPR signal to draw a ferromagnetic-like hysteresis loop (Figure 22a). These results suggest that the positive magneto-LC effect is driven by collective alignment of LC molecules and the subsequent breaking of its space inversion symmetry.

As one of the origins of nonlinear ME effect, DM interactions, $E_{\mathrm{DM}}~\sum _{ij}{\mathit{D}}_{ij}·{\mathit{S}}_i\times {\mathit{S}}_j$, are known. The Dzyaloshinkii vector (D_ij) can be present when the space inversion symmetry is broken. The existence of DM interactions in LC nitroxide radicals were indicated by the anisotropic g-value (Figure 21c). Next, we discuss two possibilities for parasitic ferromagnetism on the basis of DM interactions.

The first possibility is the emergence of weak ferromagnetism accompanying the electric polarization (Figure 22a). Such weak ferromagnetism is suggested when the contribution of the energy term, E_PLM$~\mathit{P}·\left(\mathit{L}\times \mathit{M}\right)$, exists in the free energy of the system [58]. This is a phenomenological term resulting from DM interactions, where $\mathit{P}$ denotes the electric polarization, $\mathit{L}$ is antiferromagnetic vector ${\mathit{S}}_1-{\mathit{S}}_2$, and $\mathit{M}$ is the remanent magnetization perpendicular to $\mathit{L}$ (i.e., weak ferromagnetism). If $\mathit{P}$ is present in the system, the emergence of $\mathit{M}$ leads to a finite E_PLM value. Therefore, the canting of anti-ferromagnetic pairs of ${\mathit{S}}_1$ and ${\mathit{S}}_2$ to the direction perpendicular to the electric polarization can lower the total energy of the system by E_PLM (Figure 23a). As expressed in $\mathit{L}$, large anti-ferromagnetic correlations between spins by sufficient intermolecular contacts are needed for this mechanism. It is highly plausible that the large molecular mobility in the LC and isotropic phases is likely responsible for the inhomogeneous intermolecular contact (Figure 16) [47]. This picture is consistent with the results obtained from the experiment on the ME effect (Figure 22). Both the g-value and the line width (∆H_PP) are switched by the external electric field (E) when it is perpendicular to the external magnetic field H₀ (Figure 24).

The second possibility is the emergence of helical magnetism by helical alignment of LC molecules (Figure 23b). It is known that, in the helical magnetic structures, the spins ${\mathit{S}}_i$ and ${\mathit{S}}_j$ can induce the electric polarization (p_ij) to satisfy ${\mathit{p}}_{ij} ~ {\mathit{e}}_{ij}\times \left({\mathit{S}}_i\times {\mathit{S}}_j\right)$ due to inverse DM interactions, where ${\mathit{e}}_{ij}$ is the unit vector connecting the i-th and j-th sites [59]. In contrast, in the case of LC nitroxide radicals, the helical structure formed by local ${\mathit{p}}_{ij}$ from the i-th and j-th molecule might induce the helical structure of S_i and S_j. This helical magnetic structure can have the net magnetization M along the direction of the screw axis. To the best of our knowledge, although there is no example for the helical electric polarization-induced helical magnetization, our proposed mechanism is likely to explain the unique magnetic properties observed in chiral helical LC phases (Figure 10 and Figure 11) or achiral LC phases containing partial chiral helical domains (Figure 14).

As for the correlation of super-para-magnetism and electric polarization, similar magnetic properties can be found in relaxors [60]. A relaxor can be regarded as an electric version of SG because it has randomly directed ferroelectric domains called Polar Nano Regions (PNR) due to the inherent randomness and frustration in the system (Figure 25). Recently, the emergence of super-para-magnetism has been observed at high temperatures with respect to some relaxors (or the system with relaxor-like behavior) containing magnetic metal ions [61,62] (Figure 26). For the mechanism of such super-para-magnetic relaxors, the presence of DM interactions are suggested, which will give weak ferromagnetism perpendicular to the polarization of PNR [61]. In addition, the MD simulation showed that the addition of spherical apolar impurity to spheroidal polar particles produces PNR to show the typical behavior of relaxors [63]. This seems analogous to the formation of ferroelectric domains in LC nitroxide radical samples by an impurity effect (See Section 4.2).

In some of these super-para-magnetic relaxors, it was revealed that the super-para-magnetic domains were identical to PNR by estimating their sizes [61]. In the case of LC nitroxide radicals, we must clarify the detailed relationship between the magnetic and electric properties in order to uncover the mechanism for the birth and grow of super-para-magnetic domains, which will lead to the elucidation of the microscopic mechanism of positive magneto-LC effect that LC nitroxide radicals exhibited.

6. Conclusions and Prospects

Since 2008, we have reported that a series of chiral and achiral all-organic LC nitroxide radicals having one or two PROXYL units in the core position display SG-like superparamagnetic features, such as a magnetic hysteresis (referred to as positive magneto-LC effect), and thermal and impurity effects during a heating and cooling cycle in weak magnetic fields. In general, the enantiomerically-enriched rod-like LC nitroxide radicals trans-1 and their derivatives always showed a distinct positive magneto-LC effect, irrespective of the molecular positive or negative dielectric anisotropy (∆ε), whereas the corresponding racemic samples exhibited the positive or negative magneto-LC effect, depending on the negative or positive sign of molecular ∆ε, respectively. Furthermore, for the first time, the magneto-electric (ME) effect was observed in the ferroelectric (SmC*) phase of S,S-enriched 1 (m = n = 13) at temperatures as high as 75 °C. Achiral meso diradical compound (R,S)-3 became SHG-active gradually in the discotic hexagonal columnar phase by heating in the presence of a magnetic field to form a chiral helical columnar structure and eventually showed a distinct positive magneto-LC effect. It is also noticeable that a very large impurity effect was observed for this compound when 20 mol% of racemic cis-diastereomers (R*,R*)-3 was added to the host (R,S)-3 as the impurity.

By comparison of these experimental results with the well-known magnetic properties of SG materials and on the basis of the results of nonlinear ME effect, we suggest that the positive magneto-LC effect, i.e., partial formation of super-para-magnetic domains in the major paramagnetic spins in the LC phase, is most likely to originate from the emergence of weak ferromagnetism accompanying the electric polarization due to DM interactions and/or the emergence of helical magnetism by helical alignment of LC molecules.

For the practical application of the positive magneto-LC effect to organic materials science, it is essential to enlarge the ratio of superparamagnetic domains to paramagnetic spins in the LC and isotropic phases. The utilization of the impurity effect to form SG-like inhomogeneous magnetic domains is quite promising because we can select the most suitable compounds among a variety of candidate magnetic and nonmagnetic organic compounds miscible with LC phases as the impurities. The electric field control of ferromagnetic domains is another interesting choice. However, this needs further studies to understand the detailed mechanism of the positive magneto-LC effect. These studies will offer novel access to the realization and application of ferromagnetic materials composed of organic radical spins. At the same time, it will be possible to measure the AC magnetic susceptibility at low or even higher temperatures for elucidating the mechanism of positive magneto-LC effect owing to a considerable increment of the super-para-magnetic region surrounded by the para-magnetic spins.