Image Encryption Algorithm Based on Tent Delay-Sine Cascade with Logistic Map

Abstract

We propose a new chaotic map combined with delay and cascade, called tent delay-sine cascade with logistic map (TDSCL). Compared with the original one-dimensional simple map, the proposed map has increased initial value sensitivity and internal randomness and a larger chaotic parameter interval. The chaotic sequence generated by TDSCL has pseudo-randomness and is suitable for image encryption. Based on this chaotic map, we propose an image encryption algorithm with a symmetric structure, which can achieve confusion and diffusion at the same time. Simulation results show that after encryption using the proposed algorithm, the entropy of the cipher is extremely close to the ideal value of eight, and the correlation coefficients between the pixels are lower than 0.01, thus the algorithm can resist statistical attacks. Moreover, the number of pixel change rate (NPCR) and the unified average changing intensity (UACI) of the proposed algorithm are very close to the ideal value, which indicates that it can efficiently resist chosen-plain text attack.

1. Introduction

With the development of information technologies, data security has aroused wide public concern. As an important data format, images occupy a large proportion of network data. Their secure transmission plays a vital role in personal and military privacy. In recent years, many chaotic image encryption algorithms have been proposed [1,2,3,4,5,6,7,8,9,10] due to the excellent properties of chaotic maps, such as initial value sensitivity and intrinsic randomness.

Researchers have improved the single chaotic map or combined multiple chaotic maps to improve chaotic properties, producing larger secret key spaces and more random chaotic sequences. Pak et al. [3] proposed a structure to modify two same chaotic maps to produce better performance than a single map [11,12,13,14]. Li et al. [15] improved the logistic map using linear delay. Zhou et al. [6] proved that cascading chaotic maps can increase the Lyapunov exponent, and many chaotic maps can be generated with the cascade model. Hua et al. [4] combined the logistic map and sine map to generate a two-dimensional (2D) map. This paper proposes a new framework that combines the cascade model and delay. This framework rationally integrates three chaotic maps to overcome the performance flaws of one-dimensional (1D) chaotic maps [16]. The experimental results showed that the chaotic maps produced by this model have initial value sensitivity and a large parameter interval.

Based on the proposed chaotic map, we constructed a new image encryption algorithm. Generally, image encryption algorithms can be divided into two steps: confusion and diffusion. Confusion involves randomly changing the position of pixels. The two commonly used confusion algorithms are: performing row and column confusion on a image, and reshaping a two-dimensional image into a vector, and then performing position confusion on it [17,18,19]. The basic diffusion methods are based on an XOR operation or mod operation after addition [20,21].

In this paper, a new simultaneous confusion and diffusion algorithm is proposed, which is applied in the vertical and horizontal directions based on an XOR operation. After analysis, the algorithm can resist chosen-plain text attacks and statistical attacks.

The rest of the paper is organized as follows. In Section 2, the proposed chaotic map is introduced. Section 3 shows the details of the image encryption algorithm. The proposed algorithm is analyzed and compared with other works in Section 4. Section 5 concludes the work.

2. Chaotic Map

This section proposes a new chaotic map with delay and cascade using tent, sine, and logistic maps, which we have named tent delay-sine cascade with logistic map (TDSCL). Through the combination of these three kinds of maps, we verified that this new chaotic map has excellent chaotic complexity using the following analysis and comparison.

2.1. The Structure of Chaotic Maps

First, this section reviews three chaotic maps including tent map, sine map, and logistic map. Based on these three chaotic maps, the TDSCL map is generated. The tent map is defined mathematically as [22]:

$$x_{n+1}=T_{\lambda }\left(x_n\right)=\left\{\begin{array}{c}2\lambda x_{n}for{x}_n<0.5\hfill \\ 2\lambda (1-x_n)for{x}_n\ge 0.5\hfill \end{array}\right.$$

(1)

where $\lambda$ is the control parameter with the range of [0, 1].

The structure of the sine map is defined as [23]:

$$x_{n+1}=S_{\alpha }\left(x_n\right)=\alpha sin\left(\pi x_n\right)$$

(2)

where $\alpha$ is the control parameter with a range of [0, 1], and the map is chaotic with $\alpha \in (0.87,1)$. For all $n\ge 1$, $x_n$ is bounded within [0, 1]. The diagrams of bifurcation are shown in Figure 1b.

The logistic map is a simple 1D chaotic map. As a discrete chaotic map, Figure 1c shows its bifurcation, with outputs in the range of [0, 1] and an initial input value in [0, 1]. The structure of the logistic map is defined by [24]:

$$x_{n+1}=L_{\mu }\left(x_n\right)=4\mu x_n(1-x_n)$$

(3)

where $\mu$ is the control parameter in the range of [0, 1].

The above three chaotic maps all have flaws, producing no chaotic behavior in some ranges of parameters. Specifically, these three maps only show chaotic characteristics at the rightmost part of the parameter variation range, and the chaotic interval may be discontinuous. To overcome these flaws, we designed a novel chaotic map structure, which is shown in Figure 2. As shown in Figure 2, $T\left(x\right)$ represents the tent map with a delay item input, and the sine map is indicated by $S\left(x\right)$. Then, the outputs of $T\left(x\right)$ and $S\left(x\right)$ are added as the input of $f\left(x\right)$. The function $f\left(x\right)$ is taken as $e^x$ in this paper, and cascaded with $L\left(x\right)$, thereby obtaining the output result of the chaotic map.

$$x_{n+1}=\mu f\circ F\left(x_n\right)(1-f\circ F\left(x_n\right))mod1$$

(4)

$$F\left(x_n\right)=\left\{\begin{array}{c}2x_{n-1}+sin\left(\pi x_n\right)x_n<0.5\hfill \\ 2(1-x_{n-1})+sin\left(\pi x_n\right)x_n\ge 0.5\hfill \end{array}\right.$$

(5)

Here, the control parameters for the tent map and the sine map are set to 1, and the parameter $\mu$ for the logistic map is used as the control parameter for this new map. Equations (4) and (5) show the mathematical formulae. The circle symbol in Equation (4) represents the composition of two functions. Compared to the 1D delay and linearly coupled logistic chaotic map (DLCL) [15] and a two-dimensional logistic-modulated sine-coupling logistic chaotic map (LSMCL) [1], the structure of TDSCL produces better chaotic performance. In the following section, we use the trajectory, Lyapunov exponent, and permutation entropy (PE) to analyze the characteristics of chaotic maps.

2.2. Chaotic Performance of TDSCL

2.2.1. Chaotic Trajectory

For a chaotic system, the trajectory on the phase plane can show the randomness of outputs [25]. The larger the space occupied by the trajectory, the better the random outputs of the chaotic systems. Figure 3 shows the trajectories of TDSCL, DLCL, and LSMCL. The trajectory of TDSCL can fill the entire phase space compared to DLCL and LSMCL. This indicates that the sequence generated by the TDSCL chaotic map has better randomness and ergodicity.

2.2.2. Lyapunov Exponent

One of the most important features of a chaotic system is a strong sensitivity to initial values. The Lyapunov exponent (LE) [26] provides a quantitative description of the initial state sensitivity of a chaotic system. A maximum Lyapunov exponent of the chaotic map greater than 0 indicates that the system is in a chaotic state. For a two-dimensional chaotic system, if the system’s two Lyapunov exponents are greater than 0, then the system is in a hyperchaotic state.

In Figure 4a–c, the Lyapunov exponents of TDSCL, DLCL, and LSMCL are calculated. From these diagrams, TDSCL displays hyperchaotic behavior when approximately $\mu \in (0.05,1]$. When $\mu =1$, the maximum Lyapunov exponent of TDSCL is close to 9.2. Therefore, compared with the other two maps, TDSCL not only has a larger chaotic state interval, but also a larger Lyapunov exponent in a large continuous interval. Compared with DLCL and LSMCL, TDSCL is more sensitive to small changes in the initial value of the system and has better unpredictability.

2.2.3. Permutation Entropy

The permutation entropy can be used to measure the complexity of chaotic sequences [27]. For a given chaotic system, an entropy of the generated chaotic sequence close to 1 indicates that the chaotic system has unpredictability. As shown in Figure 5, the PE of DLCL is close to 1, only when $\mu$ in the interval of [0.7, 1], and the permutation entropy of LSMCL is always less than 0.8. The permutation entropy value of TDSCL is very close to 1 when $\mu \in [0.1,1]$. This indicates that the chaotic sequences generated by TDSCL have more complex dynamic behaviour.

3. Image Encryption Algorithm

In the proposed algorithm, the secret key consists of 16 parameters {$x_1\left(1\right)$, $x_1\left(2\right)$, $n_1$, $u_1$, $x_2\left(1\right)$, $x_2\left(2\right)$, $n_2$, $u_2$, $x_3\left(1\right)$, $x_3\left(2\right)$, $n_3$, $u_3$, $x_4\left(1\right)$, $x_4\left(2\right)$, $n_4$, and $u_4$}, where $x_i\left(1\right),x_i\left(2\right)$ are the first two values of the chaotic sequence, $u_i$ is the control parameter of the chaotic map, and $n_i$ is related to the length of the generated chaotic sequence. 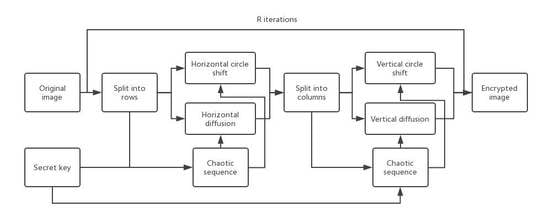As shown in Figure 6, the first step in the encryption algorithm obtaining chaotic sequences is based on the key. Then, confusion and diffusion are performed simultaneously. The details of the algorithm are introduced below.

3.1. Simultaneous Horizontal Confusion and Diffusion

• Step 1. Generate diffusion matrix $S_1$.

Iterate Equation (4) $n_1+M\times N$ times with initial value $x_1\left(1\right),x_1\left(2\right)$ and control parameter $u_1$. $M,N$ are the height and width of the image I that is being processed, respectively. Then, the diffusion matrix $S_1$ is obtained by the generated chaotic sequence $x_1$ using Equation (6).

$$S_1(i,j)=⌊x_1(n_1+(i-1)\times M+j)\times {10}^6⌋mod256.$$

(6)

where $i=1,2,\dots ,M$ and $j=1,2,\dots ,N$. $S_1$ is the matrix of M by N, each value of which is derived from the chaotic sequence $x_1$. With the given parameter $u_1$, the generated chaotic sequence $x_1$ has considerable randomness.

• Step 2. Set $i=1$.
• Step 3. Obtain begin index $b_1^i$ and circle shift the first row of the image $I(1,:)$ right by $t_1^i$ pixels

Obtain $x_2\left(1\right),x_2\left(2\right),n_2,u_2$ from the secret key and and calculate the initial value as well as iteration time of chaotic map by adjusting them with the pixel value of image I according to Equation (7).

$$\left\{\begin{array}{c}\begin{array}{l}{x}_2^i\left(1\right)=(x_2\left(1\right)+I(r_i,1)/255)mod1,\hfill \\ x_2^i\left(2\right)=x_2\left(2\right),\hfill \\ n_2^i=n_2+I(r_i,N)\hfill \end{array}\end{array}\right.$$

(7)

where:

$$r_i=\left\{\begin{array}{c}\begin{array}{cc}M,\hfill & \hfill i=1\\ i-1,\hfill & \hfill else.\end{array}\end{array}\right.$$

(8)

Then, using initial value $x_2^i\left(1\right),x_2^i\left(2\right)$ and parameter $u_2$, iterate Equation (4) $n_2^i+2$ times. Obtain $b_1^i$ and $t_1^i$ according to Equation (9).

$$\left\{\begin{array}{c}\begin{array}{c}{b}_1^i=⌊x_2^i(n_2^i+1)\times {10}^6⌋modN\hfill \\ t_1^i=⌊x_2^i(n_2^i+2)\times {10}^6⌋modN.\hfill \end{array}\end{array}\right.$$

(9)

• Step 4. Horizontal diffusion.

The horizontal diffusion operation is performed based on the XOR operation. The operation process is as follows:

$$\begin{array}{c}forj=1:N\hfill \\ ifj=1\hfill \\ I(i,c_j)=I(i,c_j)\oplus S_1(i,j)\hfill \\ else\hfill \\ I(i,c_j)=I(i,c_{j-1})\oplus I(i,c_j)\oplus S_1(i,j)\hfill \\ endif\hfill \\ endfor\hfill \end{array}$$

where

$$c_j=\left\{\begin{array}{c}\begin{array}{cc}{b}_1^i,\hfill & \hfill j=1\\ N,\hfill & \hfill (b_1^i+j-1)=N\\ (b_1^i+j-1)modN,\hfill & \hfill else.\end{array}\end{array}\right.$$

(10)

• Step 5. Circle shift $I(i,:)$ horizontally by $t_1^i$ pixels.
• Step 6. Let $i=i+1$ and repeat steps 3 to 5 until all rows have been processed.

3.2. Simultaneous Vertical Confusion and Diffusion

The simultaneous operation of vertical confusion and diffusion is similar to the process introduced in the subsection above.

• Step 1. Generate diffusion matrix $S_2$.

Iterate the formula in Equation (4) $n_3+M\times N$ times with initial value $x_3\left(1\right),x_3\left(2\right)$ and control parameter $u_3$. Then, the diffusion matrix $S_3$ is obtained according to:

$$S_2(k,l)=⌊x_3(n_3+(k-1)\times M+l)\times {10}^6⌋mod256.$$

(11)

where $k=1,2,\dots ,M$ and $l=1,2,\dots ,N$.

• Step 2. Set $l=1$.
• Step 3. Generate index $b_2^l$ and circle shift the first column of the image $I(:,1)$ by $t_2^l$ pixels.

Obtain $x_4\left(1\right),x_4\left(2\right),n_4,u_4$ from the secret key and adjust them with the pixel value of image I according to Equation (12).

$$\left\{\begin{array}{c}\begin{array}{c}{x}_4^l\left(1\right)=(x_4\left(1\right)+I(1,p_l)/255)mod1,\hfill \\ x_4^l\left(2\right)=x_4\left(2\right),\hfill \\ n_4^l=n_4+I(M,p_l)\hfill \end{array}\end{array}\right.$$

(12)

where:

$$p_l=\left\{\begin{array}{c}\begin{array}{cc}N,\hfill & \hfill l=1\\ l-1,\hfill & \hfill else.\end{array}\end{array}\right.$$

(13)

Then, using the initial value $x_4^l\left(1\right),x_4^l\left(2\right)$ and parameter $u_4$, iterate Equation (4) $n_4^l+2$ times. Obtain $b_2^l$ and $t_2^l$ according to Equation (14).

$$\left\{\begin{array}{c}\begin{array}{c}{b}_2^l=⌊x_4^l(n_4^l+1)\times {10}^6⌋modN\hfill \\ t_2^l=⌊x_4^l(n_4^l+2)\times {10}^6⌋modN.\hfill \end{array}\end{array}\right.$$

(14)

• Step 4. Vertical diffusion.

The vertical diffusion process is as follows:

$$\begin{array}{c}fork=1:M\hfill \\ ifk=1\hfill \\ I(q_k,l)=I(q_k,l)\oplus S_2(k,j)\hfill \\ else\hfill \\ I(q_k,l)=I(q_{k-1},l)\oplus I(q_k,l)\oplus S_2(k,l)\hfill \\ endif\hfill \\ endfor\hfill \end{array}$$

where:

$$q_k=\left\{\begin{array}{c}\begin{array}{cc}{b}_2^l,\hfill & \hfill k=1\\ M,\hfill & \hfill (b_2^l+k-1)=M\\ (b_2^l+k-1)modM,\hfill & \hfill else.\end{array}\end{array}\right.$$

(15)

• Step 5. Circle shift $I(:,l)$ vertically by $t_2^l$ pixels.
• Step 6. Let $l=l+1$, and repeat steps 3 to 5 until all columns have been processed.

4. Experiment Results and Analysis

4.1. Simulation Results

To verify the feasibility of the encryption algorithm proposed in this paper, some pictures were used for testing. Figure 7 shows the original images in the first column, the encrypted images in the second column, and the decrypted images in the last column.

4.2. Secret Key Space

In the proposed algorithm, the secret key contains 16 parameters. The parameters of the chaotic map are double precise, and the parameters related to the number of iterations are in the range of 0 to 1000. Thus, the secret key space can reach $0.81\times {10}^{192}>2^{637}$, which is large enough to resist statistical attacks.

4.3. Statistical Analysis

4.3.1. Correlation Coefficient Analysis

In plain images, the correlation between adjacent pixels is fairly strong, and the correlation between adjacent pixels can be used by the attacker to obtain some useful information. Therefore, after image encryption, the correlation between adjacent pixels of the encrypted image is closer to 0, indicating that the pixel distribution is random. We selected 4000 pairs of adjacent pixels in plain images and encrypted images, and then calculated the correlation coefficient of two horizontal, vertical and diagonal adjacent pixels using Equation (16):

$$C_{xy}=\frac{E\left\{\right[x-E\left(x\right)\left]\right[y-E\left(y\right)\left]\right\}}{\sqrt{D\left(x\right)}\sqrt{D\left(y\right)}}$$

(16)

where $E\left(x\right)$ and $D\left(x\right)$ represent the expectation and variance of variable x, respectively.

Table 1. The correlation coefficient in three directions for tested images.

Color Image		Horizontal	Vertical	Diagonal
4.2.01.tiff	original	0.9723	0.9843	0.9602
	encrypted	0.0001	0.0013	0.0040
4.2.02.tiff	original	0.9347	0.9413	0.8860
	encrypted	−0.0032	−0.0044	0.0011
4.2.03.tiff	original	0.8736	0.8261	0.7843
	encrypted	0.0075	−0.0012	−0.0014
4.2.04.tiff	original	0.9456	0.9727	0.9213
	encrypted	−0.0040	0.0042	0.0063
4.2.05.tiff	original	0.9364	0.9302	0.8819
	encrypted	0.0007	0.0022	−0.0007
4.2.06.tiff	original	0.9581	0.9564	0.9282
	encrypted	0.0049	−0.0002	−0.0029
4.2.07.tiff	original	0.9634	0.9704	0.9363
	encrypted	−0.0043	−0.0004	−0.0008

shows the experimental results of the tested images by performing the encryption in two rounds. The correlation coefficient of three directions is close to 0 after the encryption.

Figure 8 shows the correlation of the Lena image and its cipher image. The adjacent pixel pairs of the plain image in all directions are densely on the line of $y=x$, and the adjacent pixel pairs of the cipher image in all directions are evenly distributed in the rectangular area.

4.3.2. Histogram Analysis

An image histogram can reflect the frequency distribution of pixel values in an image [15]. In this experiment, Figure 9 shows the histograms of the plain and cipher images. The histogram of the cipher image has a balanced pixels distribution. This indicates that it is difficult for the attackers to obtain valid statistical information from the encrypted image. As the pixel values of the encrypted image have no obvious regularity, the attacker cannot obtain the original image through brute force analysis of the cipher. Therefore, the encryption system proposed in this paper has the ability to resist statistical attacks.

4.4. Key Sensitivity Test

Key sensitivity can be tested by the number of pixel change rate (NPCR) and the unified average changing intensity (UACI) [28]. In this test, we calculated the NPCR and UACI of two encrypted images based on changing a small value, set to ${10}^{-15}$ for keys. The mathematical formulas for calculating NPCR and UACI are defined as [29]:

$$\left\{\begin{array}{l}NPCR=\sum _{j=1}^M\sum _{j=1}^N\frac{D(i,j)}{M\times N}\times 100\%,\\ UACI=\sum _{j=1}^M\sum _{j=1}^N\frac{\left|C(i,j)-C‘(i,j)\right|}{255\times M\times N}\times 100\%,\end{array}\right.$$

(17)

$$D(i,j)=\left\{\begin{array}{c}0,ifC(i,j)=C\prime (i,j)\hfill \\ 1,ifotherwise\hfill \end{array}\right.$$

(18)

where $C(i,j)$ and $C\prime (i,j)$ are the cipher image generated by the original key and the changed key in the key sensitivity test, respectively. The ideal values of NPCR and UACI are 99.6094% and 33.4635% for an 8-bit grey scale image, respectively [1].

Table 2. The number of pixel change rate (NPCR) and the unified average changing intensity (UACI) of different images for key sensitivity.

Image	NPCR	UACI
4.2.01.tiff	0.9959	0.3354
4.2.02.tiff	0.9960	0.3340
4.2.03.tiff	0.9958	0.3345
4.2.04.tiff	0.9958	0.3349
4.2.05.tiff	0.9962	0.3354
4.2.06.tiff	0.9962	0.3357
4.2.07.tiff	0.9960	0.3356

lists the simulation results. The NPCR and UACI of our proposed algorithm are very close to the expected value. The analysis results showed that the algorithm can resist chosen-plain text attacks.

4.5. Resistance Against Chosen-plain Text Attack

To resist chosen-plain text attacks, an encryption system must have strong plaintext sensitivity. Similarly, plaintext sensitivity can use the same key to encrypt two distinct plaintext images, and calculate the NPCR and UACI values of the two images. We calculated the average NPCR and UACI for obtaining two cipher images 200 times, by performing two rounds of encryption in

Table 3. The NPCR and UACI of chosen-plain text analysis.

Image	NPCR	UACI
4.2.01.tiff	0.9961	0.3348
4.2.02.tiff	0.9961	0.3345
4.2.03.tiff	0.9961	0.3346
4.2.04.tiff	0.9961	0.3352
4.2.05.tiff	0.9961	0.3348
4.2.06.tiff	0.9961	0.3350
4.2.07.tiff	0.9961	0.3351

.

4.6. Information Entropy

Information entropy reflects the uncertainty of an image [30]. The larger the entropy, the greater the uncertainty. The entropy of an image was calculated according to Equation (19)

$$H=-\sum _{i=0}^{L}p\left(i\right){log}_{2}p\left(i\right)$$

(19)

where L is the number of pixel grey levels, and $p\left(i\right)$ is the probability that the grey value i appears. From

Table 4. The information entropy of different images.

Image	Entropy
4.2.01.tiff	7.9969
4.2.02.tiff	7.9973
4.2.03.tiff	7.9973
4.2.04.tiff	7.9972
4.2.05.tiff	7.9971
4.2.06.tiff	7.9973
4.2.07.tiff	7.9971

, the information entropy of the encrypted images approaches the ideal value of eight, which indicates that the encrypted images have considerable uncertainty.

4.7. Comparison with Other Methods

Table 5. Comparison of the proposed method and other methods.

Paper	Correlation			NPCR	UACI	Entropy
	Horizontal	Vertical	Diagonal
Paper [31]	0.0062	0.0074	0.0009	0.9942	0.3352	7.9974
Paper [32]	0.0054	0.0089	0.0021	0.9965	0.3351	7.9970
Paper [2]	0.0028	0.0041	0.0010	0.9962	0.3363	7.9970
Proposed with one iteration	0.0001	−0.0007	−0.0025	0.9961	0.3344	7.9971
Proposed with two iteration	0.0007	−0.0022	−0.0007	0.9961	0.3346	7.9977

compares the correlation coefficient, the ability against chosen-plain text attacks, and information entropy between the proposed algorithm and others’ using 4.2.05.tiff. Our algorithm performs one and two rounds of encryption, and the results are listed in Table 5. The correlation coefficient of our algorithm is closer to 0, which indicates that the encrypted image has less visible information using our algorithm. For NPCR and UACI, our proposed algorithm is closer to the ideal values compared with the other three algorithms. This algorithm has a good ability to resist chosen-plain text attacks.

Moreover, the entropy of the encrypted image using the proposed algorithm with two iterations is larger than others. We show that the entropy of the encrypted image with two iterations is larger than that of one iteration.

4.8. Encryption Efficiency Analysis

In this paper, the simulation is performed on Inter(R) Core(TM) i7-6700K CPU @ 4.00 GHz with 16.0 GB in MATLAB R2019b. The average encryption time of a 256 × 256 image is 0.425 s, and the decrypted time is 0.452 s. To analyze the proposed encryption algorithm, the encryption throughput (ET) and number of cycles [33] are calculated by:

$$ET=\frac{Imag{e}_{size}\left(byte\right)}{Encryptio{n}_{time}\left(second\right)},$$

(20)

$$Numberofcyclesperbyte=\frac{CP{U}_{speed}\left(Hertz\right)}{ET\left(byte\right)}.$$

(21)

The ET of the proposed algorithm is 0.1471 MBps (million byte per second) and the algorithm needs 25,932.68 cpu cycles to finish one-byte operation.

5. Conclusions

In this paper, we constructed a new chaotic map, named TDSCL, which combines the delay tent map with the sine map, which is then cascaded with the logistic map. Compared with the DLCL and LSMCL methods, the simulation results indicated with the chaotic map that our proposed method has a larger Lyapunov exponent and permutation entropy, which demonstrates that it has a better initial value sensitivity and randomness. In addition, we proposed an image encryption algorithm with simultaneous confusion and diffusion in the vertical and horizontal directions. We analyzed the algorithm in terms of the key space, key sensitivity, ability against chosen-plain text attacks, and information entropy. The simulation results showed that this algorithm can resist statistical attacks and chosen-plain text attacks.