Stability Analysis of a Diffusive Three-Species Ecological System with Time Delays
Abstract
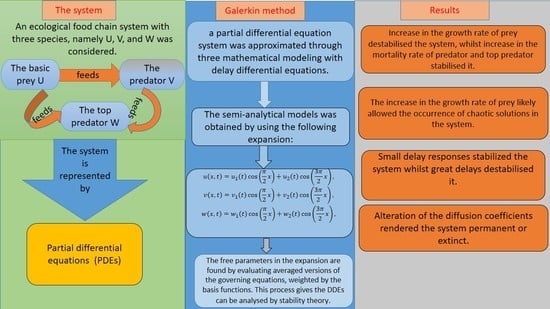
:1. Introduction
2. Mathematical Model and Methods
2.1. Mathematical Model
2.2. Galerkin Method
3. Positive Steady-State Analysis and Profiles
4. Hopf Bifurcations and Stability Analysis
4.1. Theoretical Framework
4.2. Hopf Bifurcation Maps and Limit Cycle
5. Bifurcation Diagrams
6. Conclusions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
References
- Alfifi, H.Y.; Marchant, T.R.; Nelson, M.I. Generalised Diffusive Delay Logistic Equations: Semi-analytical solutions. Dyn. Contin. Discret. Ser. B. 2012, 19, 579–596. [Google Scholar]
- Chen, S.; Shi, J. Stability and Hopf bifurcation in a diffusive logistic population model with nonlocal delay effect. J. Differ. Equ. 2012, 12, 3440–3470. [Google Scholar] [CrossRef] [Green Version]
- Su, Y.; Wei, J.; Shi, J. Hopf Bifurcation in a Diffusive Logistic Equation with Mixed Delayed and Instantaneous Density Dependence. J. Dyn. Differ. Equ. 2012, 24, 897–925. [Google Scholar] [CrossRef]
- Alfifi, H. Stability and Hopf bifurcation analysis for the diffusive delay logistic population model with spatially heterogeneous environment. Appl. Math. Comput. 2021, 408, 126362. [Google Scholar] [CrossRef]
- Hastings, A.; Powell, T. Chaos in a Three-Species Food Chain. Ecology 1991, 72, 896–903. [Google Scholar] [CrossRef]
- Song, Y.; Peng, Y.; Wei, J. Bifurcations for a predator-prey system with two delays. J. Math. Anal. Appl. 2008, 337, 466–479. [Google Scholar] [CrossRef] [Green Version]
- Yang, R.; Zhang, C. Dynamics in a diffusive predator-prey system with a constant prey refuge and delay. Nonlinear Anal. Real World Appl. 2016, 31, 1–22. [Google Scholar] [CrossRef]
- Lotka, A. Elements of Physical Biology; Williams & Wilkins Company: Baltimore, MD, USA, 1925. [Google Scholar]
- Hacinliyan, A.S.; Kusbeyzi, I.; Aybar, O.O. Approximate solutions of Maxwell Bloch equations and possible Lotka-Volterra type behavior. Nonlinear Dyn. 2010, 62, 17–26. [Google Scholar] [CrossRef]
- Faria, T. Stability and bifurcation for a delayed predator-prey model and the effect of diffusion. Math. Anal. Appl. 2001, 254, 433–463. [Google Scholar] [CrossRef] [Green Version]
- Yan, X.; Chu, Y. Stability and bifurcation analysis for a delayed Lotka-Volterra predator-prey system. Comput. Appl. Math. 2006, 196, 198–210. [Google Scholar] [CrossRef] [Green Version]
- Chen, S.; Shi, J.; Wei, J. A note on Hopf bifurcations in a delayed diffusive Lotka-Volterra predator-prey system. Comput. Math. Appl. 2011, 62, 2240–2245. [Google Scholar] [CrossRef] [Green Version]
- Tahara, T.; Gavina, M.; Kawano, T.; Tubay, J.; Rabajante, J.; Ito, H.; Morita, S.; Ichinose, G.; Okabe, T.; Togashi, T.; et al. Asymptotic stability of a modified Lotka-Volterra model with small immigrations. Sci. Rep. 2018, 8, 7029. [Google Scholar] [CrossRef] [PubMed]
- Al Noufaey, K.S.; Marchant, T.R.; Edwards, M.P. Semi-analytical solutions for the diffusive Lotka-Volterra predator-prey system with delay. Math. Biosci. 2015, 270, 30–40. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Shenghu, X. Dynamics of a general prey-predator model with prey-stage structure and diffusive effects. Comput. Math. Appl. 2014, 68, 405–423. [Google Scholar]
- Alsakaji, H.J.; Kundu, S.; Rihan, F.A. Delay differential model of one-predator two-prey system with Monod-Haldane and holling type II functional responses. Appl. Math. Comput. 2021, 397, 125919. [Google Scholar] [CrossRef]
- Gakkhar, S.; Naji, R. Chaos in three species ratio dependent food chain. Chaos Solitons Fractalas 2002, 14, 771–778. [Google Scholar] [CrossRef]
- Gilpin, M.E. Spiral chaos in a predator-prey model. Am. Nat. 1979, 107, 306–308. [Google Scholar] [CrossRef]
- Mbava, W.; Mugisha, J.; Gonsalves, J. Prey, predator and super-predator model with disease in the super-predator. Appl. Math. Comput. 2017, 297, 92–114. [Google Scholar] [CrossRef]
- Schaffer, W. Order and chaos in ecological systems. Ecology 1995, 66, 93–106. [Google Scholar] [CrossRef]
- Naji, R.K.; Balasim, A.T. Dynamical behavior of a three species food chain model with Beddington-DeAngelis functional response. Chaos Solitons Fractals 1995, 32, 1853–1866. [Google Scholar] [CrossRef]
- Pao, C. Global asymptotic stability of Lotka-Volterra 3-species reaction-diffusion systems with time delays. J. Math. Anal. Appl. 2003, 281, 186–204. [Google Scholar] [CrossRef] [Green Version]
- Liao, M.; Tang, X.; Xu, C. Dynamics of a competitive Lotka-Volterra system with three delays. Appl. Math. Comput. 2011, 217, 10024–10034. [Google Scholar] [CrossRef]
- Klebanoff, A.; Hastings, A. Chaos in three-species food chains. J. Math. Biol. 1994, 32, 427–451. [Google Scholar] [CrossRef]
- Zhao, M.; Lv, S. Chaos in a three-species food chain model with a Beddington-DeAngelis functional response. Chaos, Solitons Fractals 2009, 40, 2305–2316. [Google Scholar] [CrossRef]
- Thompson, H.B.; Do, Y.; Baek, H.; Lim, Y.; Lim, D. A Three-Species Food Chain System with Two Types of Functional Responses. Abstr. Appl. Anal. 2011, 2011, 1–16. [Google Scholar]
- Galerkin, B.G. Rods and plates. Series occurring in various questions concerning the elastic equilibrium of rods and plates. Eng. Bull. (Vestn. Inszh. Tech.) 1915, 19, 897–908. [Google Scholar]
- Marchant, T.R. Cubic autocatalytic reaction-diffusion equations: Semi-analytical solutions. Proc. R. Soc. Lond. A 2002, 458, 873–888. [Google Scholar] [CrossRef] [Green Version]
- Al Noufaey, K.S. Semi-analytical solutions of the Schnakenberg model of a reaction-diffusion cell with feedback. Results Phys 2018, 9, 609–614. [Google Scholar] [CrossRef]
- Al Noufaey, K.S. A semi-analytical approach for the reversible Schnakenberg reaction-diffusion system. Results Phys 2020, 16, 102858. [Google Scholar] [CrossRef]
- Al Noufaey, K.S. Stability analysis for Selkov-Schnakenberg reaction-diffusion system. Open Math. 2021, 19, 46–62. [Google Scholar] [CrossRef]
- Al Noufaey, K.S.; Marchant, T.R. Semi-analytical solutions for the reversible Selkov model with feedback delay. Appl. Math. Comput. 2014, 232, 49–59. [Google Scholar] [CrossRef] [Green Version]
- Al Noufaey, K.S.; Marchant, T.R.; Edwards, M.P. A semi-analytical analysis of the stability of the reversible Selkov model. Dynam. Cont. Dis. Ser. B. 2015, 22, 117–139. [Google Scholar]
- Alfifi, H. Semi-analytical solutions for the diffusive logistic equation with mixed instantaneous and delayed density dependence. Adv. Differ. Equ. 2020, 162. [Google Scholar] [CrossRef]
- Alfifi, H.Y. Semi-analytical solutions for the Brusselator reaction-diffusion model. ANZIAM J. 2017, 59, 167–182. [Google Scholar] [CrossRef]
- Alfifi, H.Y. Feedback Control for a Diffusive and Delayed Brusselator Model: Semi-Analytical Solutions. Symmetry 2021, 13, 725. [Google Scholar] [CrossRef]
- Alfifi, H.Y.; Marchant, T.R.; Nelson, M.I. Semi-analytical solutions for the 1 and 2-D diffusive Nicholson’s blowflies equation. IMA J. Appl. Math. 2012, 79, 175–199. [Google Scholar] [CrossRef]
- Alharthi, M.R.; Marchant, T.R.; Nelson, M.I. Semi-analytical solutions for cubic autocatalytic reaction-diffusion equations; the effect of a precursor chemical. ANZIAM J. 2012, 53, C511–C524. [Google Scholar] [CrossRef] [Green Version]
- Alharthi, M.R.; Marchant, T.R.; Nelson, M.I. Mixed quadratic-cubic autocatalytic reaction-diffusion equations: Semi-analytical solutions. Appl. Math. Model. 2014, 38, 5160–5173. [Google Scholar] [CrossRef]
- Marchant, T.R. Cubic autocatalysis with Michaelis-Menten kinetics: Semi-analytical solutions for the reaction-diffusion cell. Chem. Eng. Sci. 2004, 59, 3433–3440. [Google Scholar] [CrossRef]
- Marchant, T.R.; Nelson, M.I. Semi-analytical solutions for one and two-dimensional pellet problems. Proc. Roy. Soc. Lond. A 2004, 460, 2381–2394. [Google Scholar] [CrossRef]
- Fagan, W.F.; Cantrell, R.S.; Cosner, C. How habitat edges change species interactions. Am. Nat. 1999, 153, 165–182. [Google Scholar] [CrossRef]
- Golubitsky, M.; Schaeffer, D.G. Singularites and Groups in Bifurcation Theory; Springer: New York, NY, USA, 1985. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Oscillations, Dynamical Systems, and Bifurcations of Vector Fields; Springer: New York, NY, USA, 1983. [Google Scholar]
- Ruan, S.; Wei, J. On the zeros of transcendental functions with applications to stability of delay differential equations with two delays. Dyn. Contin. Discret. Impuls. Syst. Ser. B Appl. Algorithms 2003, 10, 863–874. [Google Scholar]
- Gu, K.; Niculescu, S.; Chen, J. On stability crossing curves for general systemswith two delays. J. Math. Anal. Appl. 2005, 311, 231–253. [Google Scholar] [CrossRef] [Green Version]
- Barman, B.; Ghosh, B. Explicit impacts of harvesting in delayed predator-prey models. Chaos Solitons Fractals 2019, 122, 213–228. [Google Scholar] [CrossRef]
- Barman, B.; Ghosh, B. Dynamics of a spatially coupled model with delayed prey dispersal. Int. J. Model. Simul. 2021, 1–15. [Google Scholar] [CrossRef]
- Barman, B.; Ghosh, B. Role of time delay and harvesting in some predator-prey communities with different functional responses and intra-species competition. Int. J. Model. Simul. 2021, 1–19. [Google Scholar] [CrossRef]
- Ji, J.; Lin, G.; Wang, L. Effects of intraguild prey dispersal driven by intraguild predator-avoidance on species coexistence. Appl. Math. Model. 2021, 103, 51–67. [Google Scholar] [CrossRef]
- Bajeux, N.; Ghosh, B. Stability switching and hydra effect in a predator-prey metapopulation model. Biosystems. 2020, 198, 104255. [Google Scholar] [CrossRef]
- Cui, J.A.; Chen, L. The effect of diffusion on the time varying logistic population growth. Comput. Math. Appl. 1998, 36, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Glendinning, P. Stability, Instability and Chaos: An Introduction to the Theory of Nonlinear Differential Equations; Cambridge University Press: Cambridge, UK, 1994. [Google Scholar]
- Guckenheimer, J.; Holmes, P. Nonlinear Dynamics and Chaos; John Wiley and Sons: Chichester, UK, 1986. [Google Scholar]
- Kozlov, V.; Vakulenko, S. On chaos in Lotka-Volterra systems: An analytical approach. Nonlinearity 2013, 26, 2299–2314. [Google Scholar] [CrossRef]











Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Al Noufaey, K.S. Stability Analysis of a Diffusive Three-Species Ecological System with Time Delays. Symmetry 2021, 13, 2217. https://doi.org/10.3390/sym13112217
Al Noufaey KS. Stability Analysis of a Diffusive Three-Species Ecological System with Time Delays. Symmetry. 2021; 13(11):2217. https://doi.org/10.3390/sym13112217
Chicago/Turabian StyleAl Noufaey, Khaled S. 2021. "Stability Analysis of a Diffusive Three-Species Ecological System with Time Delays" Symmetry 13, no. 11: 2217. https://doi.org/10.3390/sym13112217
APA StyleAl Noufaey, K. S. (2021). Stability Analysis of a Diffusive Three-Species Ecological System with Time Delays. Symmetry, 13(11), 2217. https://doi.org/10.3390/sym13112217