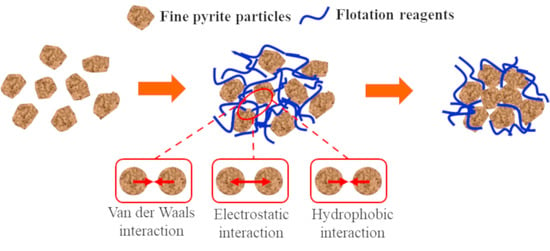
Hydrophobic Agglomeration of Fine Pyrite Particles Induced by Flotation Reagents
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Section
2.1.1. Sample Preparation and Reagents
2.1.2. Flotation Tests
2.1.3. Zeta Potential Measurements
2.1.4. Contact Angle Measurements
2.1.5. Hydrophobic Agglomeration Tests
2.2. Theoretical Background
2.2.1. Calculation of Solid Surface Energy
2.2.2. Calculation of the Interaction Energy
- a.
- Electrostatic interaction, VE (J)where εa is the absolute permittivity of water, in the unit of F/m, φ0 is the electric potential of the mineral surface, which could be obtained by zeta potential measurements, in the unit of V, κ is the thickness of the electric double-layer.
- b.
- Van der Waals interaction, VW (J)where d0 is the minimum separation distance between the surface of mineral particle and the surface of the bacteria, in the unit of nm; A1 and A2 are the hamaker constant of pyrite and water in vacuum, respectively, in the unit of J. A12 is the hamaker constant, in the unit of J.
- c.
- Hydrophobic interaction, VH (J)where k1 is the incomplete hydrophobic coefficient, θ is the contact angle, in the unit of °, h0 is the attenuation length, in the unit of m. It is worth noting that although the vast majority of evidence supports the existence of hydrophobic interactions between hydrophobic surfaces, the origin of the hydrophobia is still controversial. Therefore, Equation (9) is an empirical expression, which is calculated using the exponential decay model.
3. Results and Discussion
3.1. Microflotation Test
3.2. Zeta Potential Analysis
3.3. Contact Angle Analysis
3.4. Assessment of Hydrophobic Agglomeration Behaviors
3.5. Surface Energy and Interaction Energy Evaluation
3.5.1. Calculation and Analysis of Surface Energy
3.5.2. Calculation and Analysis of Interactions Energy between Pyrite Particles
4. Conclusions
- (1)
- Flotation tests showed that when the dosage of the activator was 6 mg/L, the dosage of a collector was 20 mg/L, the dosage of frother was 5 mg/L, and the pH value of the slurry was 6, the maximum recovery rate of pyrite was 95%. Compared to the simple addition of a single reagent, the maximum floatation of pyrite was significantly improved when multiple reagents worked together, indicating that there is a strong synergistic effect between flotation reagents, which can significantly improve the flotation environment and thus increase the recovery rate.
- (2)
- Using the contact angle measurement method, the surface energy parameters of pyrite were obtained, in which the Lifshitz-van der Waals component was 40.12 mJ/m2, the Lewis acid component was 2.55 mJ/m2, and the Lewis alkali component was 48.61 mJ/m2. The pyrite surface exhibited amphoteric properties, and the Lewis alkali component in the free energy polar component of the pyrite surface was much higher than the Lewis acid component, indicating better wettability.
- (3)
- In the medium, the van der Waals potential energy and hydrophobic interaction potential energy between pyrite particles were always less than zero, and the particles appear to attract each other. In contrast, the electrostatic interaction potential energy was greater than zero, and the particles appeared to repel each other. Flotation reagents can change the surface charge and hydrophobicity of pyrite, and directly affect the interaction potential energy between the particles. Reagent molecules were able to significantly reduce the electrostatic repulsion potential energy at the interfaces of pyrite particles and increase the interface between particles. The hydrophobic attraction potential energy enhanced the surface hydrophobicity and played a leading role in the agglomeration between particles. It was also found that the collector butyl xanthate increased the hydrophobicity of pyrite and showed the strongest aggregation behavior.
Supplementary Materials
Author Contributions
Funding
Conflicts of Interest
References
- Johnson, N.W. Liberated 0−10 µm particles from sulphide ores, their production and separation—Recent developments and future needs. Miner. Eng. 2006, 19, 666–674. [Google Scholar] [CrossRef]
- Koh, P.T.L.; Schwarz, M.P. CFD modeling of bubble-particle collision rates and deficiencies in a flotation cell. Miner. Eng. 2003, 16, 1055–1059. [Google Scholar]
- Ninham, B.W. On progress in forces since the DLVO theory. Adv. Colloid Interface Sci. 1999, 83, 1–17. [Google Scholar] [CrossRef]
- Yoon, R.H.; Mao, L. Application of extended DLVO theory, IV: Derivation of flotation rate equation from first principles. J. Colloid Interface Sci. 1996, 181, 613–626. [Google Scholar] [CrossRef]
- Vincent, B. Early (pre-DLVO) studies of particle aggregation. Adv. Colloid Interface Sci. 2012, 170, 56–67. [Google Scholar] [CrossRef]
- Song, S.; Lopez-Valdivieso, A. Parametric aspect of hydrophobic flocculation technology. Miner. Process. Extr. Metall. Rev. 2002, 23, 101–127. [Google Scholar] [CrossRef]
- Lu, S.; Song, S. Hydrophobic interaction in flocculation and flotation 1. Hydrophobic flocculation of fine mineral particles in aqueous solution. Colloids Surf. 1991, 57, 49–60. [Google Scholar] [CrossRef]
- Hu, Y.; Dai, J. Hydrophobic aggregation of alumina in surfactant solution. Miner. Eng. 2003, 16, 1167–1172. [Google Scholar] [CrossRef]
- Vos, C.F.; Davidtz, J.C.; Miller, J.D. The effect of nC12-trithiocarbonate on pyrrhotite hydrophobicity and PGE flotation. J. S. Afr. Inst. Min. Metall. 2018, 118, 1095–1102. [Google Scholar] [CrossRef] [Green Version]
- Vergouw, J.M.; Difeo, A.; Xu, Z.; Finch, J.A. An agglomeration study of sulphide minerals using zeta-potential and settling rate. Part 1: Pyrite and galena. Miner. Eng. 1998, 11, 159–169. [Google Scholar] [CrossRef]
- Wen, P.L.; Zhou, L.Y.; Zhi, Y.D. Study on the Influence of Sodium Hexametaphosphate in Ultrafine Grinding of Pyrite. Conserv. Util. Miner. Resour. 2006, 06, 13–17. [Google Scholar]
- Liu, W.P.; Yin, Z.L.; Ding, Z.Y. Influence of liquid medium on ultrafine grinding of pyrite. Chin. J. Nonferrous Met. 2007, 17, 138–143. [Google Scholar]
- Zhou, L.Y.; Zhi, Y.D.; Qi, Y.C. Study on Interaction among Pyrite Catalyst Particles Used in Direct Coal Liquefaction. Nonferrous Met. (Extr. Metall.) 2007, 06, 2–6. [Google Scholar]
- Sagit, S.L.; Abraham, M. Validity and accuracy in evaluating surface tension of solids by additive approaches. J. Colloid Interface Sci. 2003, 262, 489–499. [Google Scholar]
- Janczuk, B.; Bruque, J.M.; Gonzalez-Martin, M.L.; Roman-Galan, E. The contribution of double layers to the free energy of interactions in the cassiterite SDS solution system. Colloids Surf. A Physicochem. Eng. Asp. 1995, 100, 93–103. [Google Scholar] [CrossRef]
- Oss, C.J.V.; Giese, R.F.; Costanzo, P.M. DLVO and non-DLVO interactions in hectorite. Clays Clay Miner. 1990, 38, 151–159. [Google Scholar]
- Oss, C.J.V.; Chaudhury, M.K.; Good, R.J. Interfacial Lifshitz-van der Waals and polar interactions in macroscopic systems. Chem. Rev. 1988, 88, 927–941. [Google Scholar]
- Van Oss, C.J.; Good, R.J. Surface tension and the solubility of polymers and biopolymers: The role of polar and apolar interfacial free energies. J. Macromol. Sci. Part A Chem. 1989, 26, 1183–1203. [Google Scholar] [CrossRef]
- Oss, C.J.V.; Good, R.J.; Busscher, R.J. Estimation of the polar surface tension parameters of glycerol and formamide, for use in contact angle measurements on polar solids. J. Dispers. Sci. Technol. 1990, 11, 75–81. [Google Scholar] [CrossRef]
- Liu, J.; Xu, Z. Role of Flotation Reagents in Tuning Colloidal Forces for Sphalerite-Silica Separation. Can. Metall. Q. 2013, 46, 329–340. [Google Scholar] [CrossRef]
- Yin, W.; Xue, J.; Li, D.; Sun, Q.; Yao, J.; Huang, S. Flotation of heavily oxidized pyrite in the presence of fine digenite particles. Miner. Eng. 2018, 115, 142–149. [Google Scholar] [CrossRef]
- Chai, W.; Huang, Y.; Peng, W.; Han, J.; Cao, Y.; Liu, J. Enhanced separation of pyrite from high-sulfur bauxite using 2-mercaptobenzimidazole as chelate collector: Flotation optimization and interaction mechanisms. Miner. Eng. 2018, 129, 93–101. [Google Scholar] [CrossRef]
- Li, S.K.; Gu, G.H.; Qiu, G.Z.; Chen, Z.X. Flotation and electrochemical behaviors of chalcopyrite and pyrite in the presence of N-propyl-N′—Ethoxycarbonyl thiourea. Trans. Nonferrous Metals Soc. China 2018, 28, 1241–1247. [Google Scholar] [CrossRef]
- Feng, B.; Feng, Q.; Lu, Y. The effect of lizardite surface characteristics on pyrite flotation. App. Surf. Sci. 2012, 259, 153–158. [Google Scholar] [CrossRef]
- Bicak, O.; Ekmekci, Z.; Bradshaw, D.J.; Harris, P.J. Adsorption of guar gum and CMC on pyrite. Miner. Eng. 2007, 20, 996–1002. [Google Scholar] [CrossRef]
- Ejtemaei, M.; Nguyen, A.V. Characterisation of sphalerite and pyrite surfaces activated by copper sulphate. Miner. Eng. 2017, 100, 223–232. [Google Scholar] [CrossRef]
- Deng, W.; Xu, L.H.; Tian, J.; Hu, Y.H.; Han, Y.X. Flotation and adsorption of a new polysaccharide depressant on pyrite and talc in the presence of a pre-adsorbed xanthate collector. Minerals 2017, 7, 40. [Google Scholar] [CrossRef] [Green Version]
- Peng, Y.; Wang, B.; Gerson, A. The effect of electrochemical potential on the activation of pyrite by copper and lead ions during grinding. Int. J. Miner. Process. 2012, 102, 141–149. [Google Scholar] [CrossRef]
- López Valdivieso, A.; Sánchez López, A.A.; Song, S. On the cathodic reaction coupled with the oxidation of xanthates at the pyrite/aqueous solution interface. Int. J. Miner. Process. 2005, 77, 154–164. [Google Scholar] [CrossRef]
- Fornasiero, D.; Ralston, J. Iron hydroxide complexes and their influence on the interaction between ethyl xanthate and pyrite. J. Colloid Interface Sci. 1992, 151, 225–235. [Google Scholar] [CrossRef]
- He, S.; Fornasiero, D.; Skinner, W. Correlation between copper-activated pyrite flotation and surface species: Effect of pulp oxidation potential. Miner. Eng. 2005, 18, 1208–1213. [Google Scholar] [CrossRef]
- Wang, X.H.; Forssberg, K.S.E. Mechanisms of pyrite flotation with xanthates. Int. J. Miner. Process. 2002, 33, 275–290. [Google Scholar] [CrossRef]
- Weisener, C.; Gerson, A. An investigation of the Cu (II) adsorption mechanism on pyrite by ARXPS and SIMS. Miner. Eng. 2000, 13, 1329–1340. [Google Scholar] [CrossRef]
- Boulton, A.; Fornasiero, D.; Ralston, J. Characterisation of sphalerite and pyrite flotation samples by XPS and ToF-SIMS. Int. J. Miner. Process. 2003, 70, 205–219. [Google Scholar] [CrossRef]
- Chandra, A.P.; Puskar, L.; Simpson, D.J. Copper and xanthate adsorption onto pyrite surfaces: Implications for mineral separation through flotation. Int. J. Miner. Process. 2012, 114, 16–26. [Google Scholar] [CrossRef]
- Gu, G.H.; Wang, H.; Suo, J.; Qiu, G.Z.; Hao, Y. Interfacial interaction of bio-leaching of pyrite mineral. J. Cent. South Univ. Technol. 2008, 15, 49–53. [Google Scholar] [CrossRef]
- Ming, Q.Z.; Qi, L.; Jiong, T.L. Extended DLVO theory applied to coal slime-water suspensions. J. Cent. South Univ. 2012, 19, 3558–3563. [Google Scholar]
- Rudolph, M.; Hartmann, R. Specific surface free energy component distributions and flotabilities of mineral microparticles in flotation-An inverse gas chromatography study. Colloids Surf. A Physicochem. Eng. Asp. 2017, 513, 380–388. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, Q. Insight into the Influence of Surface Roughness on the Wettability of Apatite and Dolomite. Minerals 2020, 10, 114. [Google Scholar] [CrossRef] [Green Version]
- Chen, Z.; Nosonovsky, M. Revisiting lowest possible surface energy of a solid. Surf. Topogr. Metrol. Prop. 2017, 5, 045001. [Google Scholar] [CrossRef]
- Fowkes, F.M. Attractive Forces at Interfaces. Ind. Eng. Chem. 1964, 56, 40–52. [Google Scholar] [CrossRef]
- Good, R.J.; Girifalco, L.A. A theory for estimation of surface and interfacial energies. III. Estimation of surface energies of solids from contact angle data. J. Phys. Chem. 1960, 64, 561–565. [Google Scholar] [CrossRef]
- Hough, D.B.; White, L.R. The calculation of Hamaker constants from Liftshitz theory with applications to wetting phenomena. Adv. Colloid Interface Sci. 1980, 14, 3–41. [Google Scholar] [CrossRef]
- Drummond, C.J.; Chan, D.Y.C. Van der Waals Interaction, Surface Free Energies, and Contact Angles: Dispersive Polymers and Liquids. Langmuir 2008, 13, 3890–3895. [Google Scholar] [CrossRef]













| Composition | Fe | S | Zn | Pb | SiO2 | Others |
|---|---|---|---|---|---|---|
| Contents/% | 46.41 | 53.24 | 0.04 | 0.01 | 0.17 | 0.13 |
| Examined Liquid | γ | γLW | γLB | γ+ | γ− | Contact Angle |
|---|---|---|---|---|---|---|
| L1 (Distilled water) | 72.8 | 21.8 | 51.0 | 25.5 | 25.5 | 76.4 |
| L2 (Glycerol) | 64.0 | 34.0 | 30.0 | 3.9 | 57.5 | 16.6 |
| L3 (Diiodomethane) | 50.8 | 51.8 | 0 | 0.7 | 0 | 0 |
| Surface Energy Parameters | γLW | γLB | γ+ | γ2017 |
|---|---|---|---|---|
| Pyrite | 40.12 | 22.27 | 2.55 | 48.61 |
| Samples | φ0/mV | θ/° | k1 | h0/nm |
|---|---|---|---|---|
| Pyrite + Distilled water | −32.18 | 76.37 | 0.46 | 5.15 |
| Pyrite + Butyl xanthate | −16.14 | 87.00 | 0.51 | 5.72 |
| Pyrite + Terpineol | −10.41 | 91.00 | 0.56 | 6.26 |
| Pyrite + Cooper sulfate | −1.80 | 47.00 | 0.33 | 3.65 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, W.; Deng, Z.; Tong, X.; Lu, T. Hydrophobic Agglomeration of Fine Pyrite Particles Induced by Flotation Reagents. Minerals 2020, 10, 801. https://doi.org/10.3390/min10090801
Cheng W, Deng Z, Tong X, Lu T. Hydrophobic Agglomeration of Fine Pyrite Particles Induced by Flotation Reagents. Minerals. 2020; 10(9):801. https://doi.org/10.3390/min10090801
Chicago/Turabian StyleCheng, Wanli, Zhengbin Deng, Xiong Tong, and Tianshen Lu. 2020. "Hydrophobic Agglomeration of Fine Pyrite Particles Induced by Flotation Reagents" Minerals 10, no. 9: 801. https://doi.org/10.3390/min10090801
APA StyleCheng, W., Deng, Z., Tong, X., & Lu, T. (2020). Hydrophobic Agglomeration of Fine Pyrite Particles Induced by Flotation Reagents. Minerals, 10(9), 801. https://doi.org/10.3390/min10090801