A Fluid-Structure Interaction Method for the Elastohydrodynamic Lubrication Characteristics of Rubber-Plastic Double-Layer Water-Lubricated Journal Bearings

Abstract

This paper proposes a fluid-structure interaction (FSI) numerical calculation method for investigation of the elastohydrodynamic lubrication performance of the rubber-plastic double-layer water-lubricated journal bearings. The accuracy and rapidity of the FSI method are improved by studying the effect of mesh density and by comparing the calculation results with those in the literature. Based on the proposed method, a series of numerical simulations are carried out to reveal the influence of operating conditions and structural parameters on the lubrication performance of the rubber-plastic bearings. Numerical results show that the bush deformation of the rubber-plastic bearing is between that of the rubber bearing and the plastic bearing, and the deformation area is close to that of the rubber bearing. The bearing load carrying capacity increases significantly with the rotational speed, eccentricity ratio, bearing length, and decrease with the clearance. But the influences of the plastic layer elastic modulus and thickness on bearing load are unremarkable. The effect of bush deformation on bearing load is noticeable when the eccentricity ratio is more than 0.8. The results are expected to provide design references for the bearings.

1. Introduction

With the awareness of environmental protection becoming increasingly prominent, water-lubricated bearings are widely employed in huge ships and submarines because of their high reliability, easy maintenance and environmental protection. As the crucial component of the transmission system of marine vehicles, the performances of bearings directly impact the security and reliability of working ships [1,2]. Due to the rapid development of modern science and technology in recent years, both civil and military ships have put forward higher requirements for the performance of water-lubricated bearings to enhance service life and reduce vibration and noise during ship operation [3]. The lubrication performance of water-lubricated bearings is significantly influenced by their material composition and structural design. Therefore, it is crucial to study the lubrication performance and lubrication mechanism of water-lubricated bearings of different materials and structures [4,5].

Currently, the bush materials are mainly rubber, plastic and other elastic materials [6]. Rubber bush has high elasticity and good damping capacity; thus, it is widely used in stern bearings. However, rubber bearings have large starting torque and high friction noise at low speeds and heavy loads. Plastic bush has a low friction coefficient but poor compliance and damping performance. To achieve better bearing performance, rubber and plastic can be superposed to form rubber-plastic double-layer bush water-lubricated bearings. Yamajo et al. [7] studied the application characteristics of poly tetra fluoroethylene (PTFE) three-layer composite bearing and found that the bearing has a smaller friction coefficient, better wear resistance and longer service life than rubber bearing. Litwin [8,9] studied the lubrication characteristics of a three-layer PTFE-nitrile rubber (NBR)-bronze water-lubricated bearing with lubricating grooves by experiments. The results showed that the bearing works under a hydrodynamic lubrication state for most working conditions, and its starting and running resistance is less than those of the NBR bearing. Xie et al. [3] designed a double-liner bearing structure. The results show that the acoustic performances are closely related to the material combinations. Although studies have shown that rubber-plastic double-layer bush water-lubricated bearings have superior performance, their load-carrying mechanism and structural design method are not clear, which restricts their application.

At present, scholars have carried out extensive research on the lubrication and load-carrying mechanism of water-lubricated rubber bearings and plastic bearings. Shi et al. [10] studied the dynamic characteristics of water-lubricated rubber bearings and found that the eccentricity ratio, length-to-diameter ratio, radial clearance and rotational speed have a great influence on the bearing dynamic performance. Liu et al. [11] built a test rig to study the lubrication characteristics of water-lubricated rubber bearings at high rotating speeds. The experimental results showed that, different from the laminar flow, the bearing load increases faster as the rotating speed increases, indicating a turbulent flow at high rotating speeds. Qiao et al. [12] proposed a mixed lubrication model considering the effect of turbulence and studied the effects of axial misalignment, load, rotational speed and radial clearance on the lubrication performance of water-lubricated rubber bearings. Kuznetsov et al. [13] studied the effect of PTFE lining compliance on the bearing characteristics based on a thermohydrodynamic (THD) model including liner deformation, and the analysis showed increased load carrying capacity, significantly reduced peak pressure and thicker oil film in the loaded zone compared to a white metal bearing. Wang et al. [14] analyzed the lubrication performance of PTFE-based water-lubricated bearings using computational fluid dynamics (CFD) and fluid–structure interaction (FSI) method and studied the effects of elastic modulus and Poisson’s ratio on bearing elastic deformation and load-carrying capacity. Yang et al. [15] analyzed the lubrication performance of UHMWPE water-lubricated bearings. Cheng et al. [16] studied the tribological properties of PEEK under seawater lubrication.

The above studies showed that when the elastic deformation of the bearing bush is close to the minimum water film thickness, the bush deformation must be considered in the calculation. Currently, the literature mainly adopts two methods to study elastohydrodynamic lubrication problems, namely the CFD-FSI method [17,18] and the programming method [19]. The CFD-FSI method solves 3-dimensional fluid and solid models. It is intuitive and convenient to post-processing, but it is prone to failure when the deformation is large and causes mesh distortion [20]. The programming method solves the fluid model based on the two-dimensional Reynolds equation and calculates the elastic deformation by approximate formula or the finite element method (FEM); thus, there is no mesh distortion, and it can calculate large deformation conditions. The Reynolds equation is usually solved by the finite difference method (FDM), and good results can be obtained for circular plain bearings. The FEM can also solve the Reynolds equation, but its program structure is more complex, and the calculation time is longer. To solve the bush elastic deformation, some researchers used approximate formulas. For example, Thomsen and Klit [21] calculated the deformation of the polymer liner using the Winkler/Column model. Xiang et al. [22,23,24] and Gong et al. [25] used an influence coefficient method to determine the elastic deformation. Du et al. [26] used an approximate formula to consider bush deformation. Other literature used the FEM to calculate the bearing deformation [27,28,29,30,31,32,33]. Relative to the approximate formula, the FEM can describe the elastic deformation more accurately and has higher adaptability. Therefore, in this work, the FDM is used to solve the Reynolds equation, and the FEM is used to calculate the elastic deformation, which is a tradeoff of accuracy, applicability and computing efficiency.

In summary, scholars have conducted extensive research on the lubrication mechanisms, frictional behavior and structural design of water-lubricated rubber bearings and plastic bearings. Rubber-plastic double-layer water-lubricated bearings may achieve better performance than rubber bearings and plastic bearings. However, the research on this type of bearing is limited, and the FSI lubrication characteristics of the bearings are not very clear. The previous work [20] intended to reveal the bearing performance by the CFD-FSI method, while the results only showed the lubrication performance for small eccentricity ratios, and mesh distortion occurs and causes calculation failure for large eccentricity ratios.

In order to reveal the elastohydrodynamic lubrication characteristics of the rubber-plastic double-layer water-lubricated journal bearings and obtain bearing performance under various operating conditions, especially heavy load conditions, a two-way FSI numerical calculation method is proposed and established by solving the water film pressure based on the Reynolds equation by the FDM and solving the bush deformation by the FEM. The validity of the numerical calculation method is verified by comparing the results with the published literature results. The water film pressure and bush deformation of the bearing are compared with those of the rubber bearing and the plastic bearing. The load-carrying performance of the bearings for different eccentricity ratios, rotational speed, length-to-diameter ratio, clearance ratio and elastic modulus and thickness of the plastic layer bush are investigated. The results will provide theoretical guidance for the structural design and application of this type of bearings.

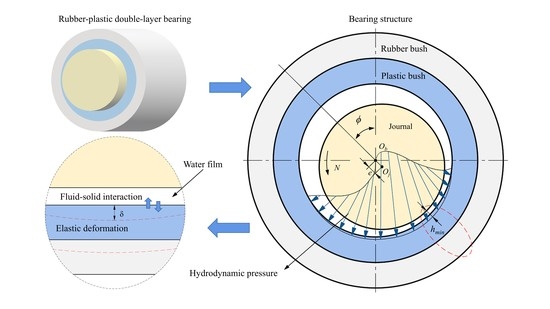
2. Geometry

The rubber-plastic double-layer water-lubricated journal bearing geometry is shown in Figure 1. O_b is the bearing center; O_j is the journal center; e is the eccentricity between the bearing and journal centers; ϕ is the attitude angle; N is the rotational speed of the journal; h_min is the minimum film thickness; D is the bearing inner diameter; L is the bearing length; t₁ is the thickness of the plastic layer bush; and t₂ is the thickness of the rubber layer bush.

3. Numerical Analysis

3.1. Water Film Fluid Model

As the water viscosity is small, the temperature rise of water-lubricated bearing is low. The water film flow is assumed to be isothermal, steady and incompressible. The Reynolds equation can be written as [34]

$$\frac{1}{R^2}\frac{\partial }{\partial \phi }\left(\frac{h^3}{12\mu }\frac{\partial p}{\partial \phi }\right)+\frac{\partial }{\partial z}\left(\frac{h^3}{12\mu }\frac{\partial p}{\partial z}\right)=\frac{U}{2R}\frac{\partial h}{\partial \phi }$$

(1)

where R (R = D/2) is the inner radius of the bearing bush; φ is the angular coordinate; h is the water film thickness; μ is the fluid dynamic viscosity; p is the hydrodynamic pressure; z is the axial coordinate; and U is the journal surface velocity.

Considering the elastic deformation of the bearing bush, the water film thickness h is expressed as

$$h=c\left(1+\epsilon \cos \phi \right)+\delta$$

(2)

where c is the radial clearance, ε is the eccentricity ratio (ε = e/c), and δ indicates the radial elastic deformation of the bearing bush.

Reynolds boundary conditions [35] are used:

$$\left\{\begin{array}{l}p(\phi ,z=-\frac{L}{2})=p(\phi ,z=+\frac{L}{2})=0\\ p({\phi }_0,z)=0\\ \frac{\partial p({\phi }_0,z)}{\partial \phi }=0\end{array}\right.$$

(3)

where φ₀ represents the water film rupture position.

The finite difference method is used to solve Equation (1). The mesh used for the calculations is set as m × n for the circumferential and axial directions, respectively. The influence of the mesh density is studied in Section 3.3 for accuracy and rapidity of the calculations. The super relaxation iteration (SOR) method [36] is used when calculating the pressure values, and all convergence residuals are taken as 10⁻⁴.

The water film load-carrying capacity W in the eccentric direction and its vertical direction can be calculated by integrating the pressure over the journal surface:

$$W_e={\displaystyle {\int }_{-L/2}^{L/2}{\displaystyle {\int }_0^{2\pi }p\cos \phi Rd\phi dz}}$$

(4)

$$W_{\phi }={\displaystyle {\int }_{-L/2}^{L/2}{\displaystyle {\int }_0^{2\pi }p\sin \phi Rd\phi dz}}$$

(5)

The water film load-carrying capacity is

$$W=\sqrt{W_e^2+W_{\phi }^2}$$

(6)

The attitude angle is

$$\varphi =-\arctan \frac{W_{\phi }}{W_e}$$

(7)

The friction torque M_f of the rotating journal is a composition of the shear flow friction torque M_f1 and the pressure flow friction torque M_f2. The shear flow friction torque M_f1 is the sum of the shear flow resistance of the water film intact area and ruptured are as follows.

$$M_{f1}=\frac{1}{2}{\displaystyle {\int }_{-L/2}^{L/2}{\displaystyle {\int }_0^{{\phi }_b}\left(\frac{\mu U}{h}\right)}}{R}^{2}d\phi dz+\frac{1}{2}{\displaystyle {\int }_{-L/2}^{L/2}{\displaystyle {\int }_{{\phi }_b}^{2\pi }\frac{\mu U{h}_b}{h^2}}}{R}^{2}d\phi dz$$

(8)

where φ_b is the angular position of the ruptured edge, and h_b is the film thickness on the edge.

The pressure flow friction torque M_f2 is

$$M_{f2}=\frac{e\sin \varphi }{2}W$$

(9)

The total friction torque M_f is

$$M_f=M_{f1}+M_{f2}$$

(10)

3.2. Bearing Bush Solid Model

The finite element method [37] is used to calculate the elastic deformation of the bearing bush. The finite element model of the rubber-plastic double-layer bearing bush is shown in Figure 2. The upper layer is the plastic bush and the lower layer is the rubber bush. The meshing method in the circumferential and axial directions is consistent with that of the fluid model. Eight-nodes hexahedron elements are used. Each node has three degrees of freedom, and the displacement field of the element can be written as

$$\underset{\left(3\times 1\right)}{u}\left(x,y,z\right)=\left[\begin{array}{c}u\\ v\\ w\end{array}\right]=\left[\begin{array}{ccc}{\mathit{N}}_1& 0& 0\\ 0& {\mathit{N}}_1& 0\\ 0& 0& {\mathit{N}}_1\end{array}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\begin{array}{ccc}⋮& {\mathit{N}}_2& 0\\ ⋮& 0& {\mathit{N}}_2\\ ⋮& 0& 0\end{array}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\begin{array}{ccc}0& ⋮& \dots \\ 0& ⋮& \dots \\ {\mathit{N}}_2& ⋮& \dots \end{array}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\begin{array}{ccc}⋮& {\mathit{N}}_8& 0\\ ⋮& 0& {\mathit{N}}_8\\ ⋮& 0& 0\end{array}\hspace{0.33em}\hspace{0.33em}\hspace{0.33em}\begin{array}{c}0\\ 0\\ {\mathit{N}}_8\end{array}\right]\cdot q^e=\underset{\left(3\times 24\right)}{\mathit{N}}\cdot \underset{\left(24\times 1\right)}{q^e}$$

(11)

where N is the shape function matrix, and q^e is the node displacement array, q^e = [u₁ v₁ w₁ u₂ v₂ w₂ … u₈ v₈ w₈]^T.

According to the geometric equations of three-dimensional problem of elasticity mechanics, the strain field of the element can be expressed as

$$\underset{\left(6\times 1\right)}{\epsilon }\left(x,y,z\right)=\left[\begin{array}{c}\begin{array}{c}{\epsilon }_{xx}\\ {\epsilon }_{yy}\\ {\epsilon }_{zz}\end{array}\\ \begin{array}{c}{\gamma }_{xy}\\ {\gamma }_{yz}\\ {\gamma }_{zx}\end{array}\end{array}\right]=\left[\begin{array}{ccc}\frac{\partial }{\partial x}& 0& 0\\ 0& \frac{\partial }{\partial y}& 0\\ 0& 0& \frac{\partial }{\partial z}\\ \frac{\partial }{\partial y}& \frac{\partial }{\partial x}& 0\\ 0& \frac{\partial }{\partial z}& \frac{\partial }{\partial y}\\ \frac{\partial }{\partial z}& 0& \frac{\partial }{\partial x}\end{array}\right]\left[\begin{array}{c}u\\ v\\ w\end{array}\right]=\underset{\left(6\times 3\right)}{\left[\partial \right]}\underset{\left(3\times 1\right)}{u}=\underset{\left(6\times 3\right)}{\left[\partial \right]}\underset{\left(3\times 24\right)}{N}\underset{\left(24\times 1\right)}{q^e}=\underset{\left(6\times 24\right)}{B}\underset{\left(24\times 1\right)}{q^e}$$

(12)

where B = [∂]N.

As the elastic modulus and Poisson’s ratio of the rubber bush and plastic bush are different, the stress field functions of the two-layer elements are different. Based on the linear elastic constitutive equation, the stress field function of the element in layer i (i = 1,2) can be expressed as

$$\underset{\left(6\times 1\right)}{{\sigma }_i}=\underset{\left(6\times 6\right)}{D_i}\underset{\left(6\times 1\right)}{\epsilon }$$

(13)

where D_i is the elastic coefficient matrix of the element in layer i (i = 1,2), and

$${\mathit{D}}_i=\frac{E_i}{\left(1+{\nu }_i\right)\left(1-2{\nu }_i\right)}\left[\begin{array}{cccccc}1-{\nu }_i& {\nu }_i& {\nu }_i& 0& 0& 0\\ {\nu }_i& 1-{\nu }_i& {\nu }_i& 0& 0& 0\\ {\nu }_i& {\nu }_i& 1-{\nu }_i& 0& 0& 0\\ 0& 0& 0& \frac{1-2{\nu }_i}{2}& 0& 0\\ 0& 0& 0& 0& \frac{1-2{\nu }_i}{2}& 0\\ 0& 0& 0& 0& 0& \frac{1-2{\nu }_i}{2}\end{array}\right]\left(i=1,2\right)$$

(14)

where ν_i is the Poisson’s ratio in layer i, and E_i is the elastic modulus in layer i.

The stiffness matrix of the element in layer i (i = 1,2) is

$$\underset{\left(24\times 24\right)}{{\mathit{K}}_i^e}={\displaystyle {\int }_{{\Omega }^e}\underset{\left(24\times 6\right)}{{\mathit{B}}^T}}\underset{\left(6\times 6\right)}{{\mathit{D}}_i}\underset{\left(6\times 24\right)}{\mathit{B}}d\Omega$$

(15)

The equivalent node load matrix of the element is

$$\underset{(24\times 1)}{{\mathit{P}}^e}={\displaystyle {\int }_{{\Omega }^e}\underset{(24\times 3)}{{\mathit{N}}^T}\underset{(3\times 1)}{\overline{\mathit{b}}}}d\Omega +{\displaystyle {\int }_{S_p^e}\underset{(24\times 3)}{{\mathit{N}}^T}}\underset{(3\times 1)}{\overline{\mathit{p}}}dA$$

(16)

The element stiffness equation is

$$\underset{(24\times 24)}{{\mathit{K}}^e}\underset{(24\times 1)}{{\mathit{q}}^e}=\underset{(24\times 1)}{{\mathit{P}}^e}$$

(17)

To solve the stiffness equation, it is necessary to introduce the boundary conditions according to the actual situation. The upper surface of the plastic layer is in direct contact with the water film, and the nodes are subjected to the hydrodynamic pressure. The lower surface of the rubber layer is in contact with the rigid bearing pedestal, and the node displacements are set as zero. The left and right sections of the bearing bush model are the same section, so the node displacements are the same. The two layers of the elastic bush fit tightly, so the node displacements are also the same.

3.3. Fluid–Solid Coupling Calculation

Figure 3 shows the flow chart of the fluid–solid coupling numerical calculation. Firstly, the initial water film thickness distribution is calculated according to the input parameters, and the steady-state Reynolds equation is solved using FDM and SOR algorithm to obtain the water film pressure distribution. Then, the elastic deformation distribution of the bearing bush is calculated using FEM, and the water film thickness distribution is updated by including the calculated deformation. The water film pressure distribution and the bush deformation distribution are recalculated until the convergence condition is reached. Finally, the load-carrying capacity, the attitude angle and the friction torque are calculated and output.

To obtain more accurate calculation results, the influence of circumferential and axial grid number, i.e., m and n, on the maximum hydrodynamic pressure and calculation time were studied. The results are shown in Figure 4. The bearing parameters and operating conditions are shown in

Table 1. Bearing parameters and operating conditions.

Parameter	Symbol	Value
Bearing diameter (mm)	D	100
Relative clearance (%)	ψ	0.4
Length-to-diameter ratio	L/D	2
Total bush thickness (mm)	t	10
Plastic bush thickness (mm)	t1	5
Rubber bush thickness (mm)	t2	5
Plastic bush elastic modulus (MPa)	E1	700
Rubber bush elastic modulus (MPa)	E2	40
Plastic bush Poisson’s ratio	ν1	0.46
Rubber bush Poisson’s ratio	ν2	0.497
Eccentricity ratio	ε	0.9
Journal rotational speed (r/min)	N	1000
Dynamic viscosity (Pa·s)	μ	0.001

. The circumferential grid number was set as 20 for Figure 4a, and the axial grid number was set as 160 for Figure 4b. The results showed that the axial grid number n has a large effect on the calculation result, and p_max approaches a constant when n is more than 160. The circumferential grid number has a small effect on p_max, and the maximum difference is 5.25%. However, the calculation time increases exponentially as the grid number increases. Therefore, for the bearing with L/D = 2, the axial grid number 160 and the circumferential grid number 40 were used in this paper. To ensure the grid aspect ratio unchanged for models with different L/D, the circumferential grid number is always taken as 40, and the axial grid number is determined according to L/D in equal proportion.

To verify the accuracy of the calculation method, the water film pressure distribution and elastic deformation distribution were compared with the calculation results of Litwin [38] as shown in Figure 5. The bearing parameters are D = 100 mm, L = 200 mm, t₁ = t₂ = 6 mm, c = 0.15 mm, N = 660 r/min and E₁ = E₂ = 800 MPa. Figure 5 shows that the results of this work are in good agreement with Litwin’s calculation results. The difference in the maximum water film pressure is 8.5%, and the difference in the maximum elastic deformation of the bearing bush is 2.1%. Since the mesh density we used is different from that used by Litwin, we believe that the reason for the difference may be attributed to the differences in calculation conditions and mesh density.

4. Results and Discussion

4.1. Performance Comparison

Figure 6 and Figure 7 compare the water film pressure distribution, bush deformation distribution and water film thickness distribution of water-lubricated rubber bearings, rubber-plastic double-layer bearings and plastic bearings. The bearing parameters are D = 100 mm, L/D = 2, ψ = 0.2%, t = 10 mm, ε = 0.9, N = 1500 r/min and t₁ = t₂ = 5 mm for rubber-plastic double-layer bearing. The bush material properties are as shown in Table 1. The results showed that the maximum water film pressure of the three kinds of bearings differ greatly, and the values are 0.46 MPa, 0.67 MPa and 1.18 MPa, respectively. Compared with the rubber bearing, the pressure distributions of the rubber-plastic double-layer bearing and the plastic bearing are more concentrated. The bush deformation distribution is similar to the pressure distribution, and the maximum bush deformation values are 17.8 μm, 9.96 μm and 2.47 μm for the three kinds of bearings, respectively. Although the maximum pressure of the plastic bearing is the largest, its bush deformation is the smallest. The bush deformation of the rubber-plastic double-layer bearing is between those of the rubber bearing and the plastic bearing, and its distribution area is close to that of the rubber bearing. However, for φ = 220°~280°, the elastic deformation of the rubber-plastic double-layer bearing is larger than that of the rubber bearing. This is because the plastic layer bush is stiffer than the rubber layer, and the shape change of the rubber-plastic double-layer bearing is smaller than that of the rubber bearing. The bush deformation increases the minimum film thickness. The film thickness distribution of the three kinds of bearings is the same in the low-pressure region. In the high-pressure region, the water film thickness of the rubber bearing is the largest, followed by the rubber-plastic double-layer bearing and the plastic bearing.

4.2. Effect of Rotational Speed on Bearing Performance

Figure 8 shows the water film pressure distribution, the bush deformation distribution and the water film thickness distribution of rubber-plastic double-layer water-lubricated bearing for different rotational speeds. The relative clearance is set to 0.2%, the rotational speed ranges from 300 r/min to 2100 r/min, and the other parameters are the same to those in Table 1. It shows that the rotational speed has a significant effect on the pressure distribution and bush deformation distribution. As the rotational speed increases, the water film pressure, the bush deformation and the minimum film thickness increase gradually. Figure 9 summarizes the effect of rotational speed on bearing lubrication and load-carrying properties for different eccentricity ratios. It shows that the maximum pressure, the maximum bush deformation, the load-carrying capacity and friction torque increase obviously with the rotational speed, and the variation increases with the eccentricity ratio. The increase in rotational speed enhances the hydrodynamic lubrication, thus the water film pressure and the load-carrying capacity increase, which make the increases of bush deformation and the minimum film thickness. The bush deformation is decided by the pressure and the bush material properties. The load-carrying capacity is obtained by integrating the pressure on the journal surface. Thus, the bush deformation and the load-carrying capacity change the same as the bearing pressure. When the eccentricity ratio is small, the bush deformation has little effect on the minimum water film thickness, and the load-carrying capacity increases almost linearly with the rotational speed. When the eccentricity ratio is large (ε > 0.8), the minimum water film thickness is small, and the influence of bush deformation on the minimum water film thickness becomes greater, the increase in load-carrying capacity with rotational speed thus slows down. In practical applications, the bearing usually works at high eccentricity ratios, so the bush deformation cannot be ignored. Figure 10 shows the variation curve of W to ε and the dimensionless journal center locus. The arc in Figure 10b indicates the clearance circle with ε = 1. Designers can obtain the eccentricity ratio according to the load and rotational speed from Figure 10a and then check the minimum water film thickness according to Figure 9c. Figure 10b shows that the journal center locus is basically the same for different rotational speeds.

4.3. Effect of Length-to-Diameter Ratio on Bearing Performance

Figure 11 shows the water film pressure distribution, bush deformation distribution and water film thickness distribution of rubber-plastic double-layer bearing for different length-to-diameter ratios. The relative clearance is set to 0.2%; the rotational speed is 1500 r/min; L/D ranges from 0.5 to 2; and the other parameters are the same as those in Table 1. When L/D is small, the water film pressure distribution and bush deformation distribution are concentrated. The larger L/D is, the larger the distribution area of pressure and bush deformation is. However, when L/D is more than 1, the water film pressure and bush deformation change little. L/D has a small effect on the water film thickness distribution. Figure 12 shows the effect of L/D on bearing lubrication performance for different eccentricity ratios. It shows that for small L/D values, the maximum pressure increases significantly with L/D, but as L/D increases, the maximum pressure tends to a certain value. This is because the side leakage of short bearings has a large effect on the water film pressure. The longer the bearing is, the smaller the effect of side leakage is, and the maximum pressure tends to the value of the infinite length journal bearing. The changing rule of the maximum bush deformation is the same as that of the maximum pressure. As the maximum bush deformation increases only 1~3 μm when L/D increases from 0.5 to 2, the minimum water film thickness changes little. Due to the increase in bearing area, the load-carrying capacity and friction torque increase significantly with L/D. The attitude angle increases slightly. Figure 13 shows the variation curve of W to ε and the dimensionless journal center locus for different L/D. Designers can obtain the eccentricity ratio according to the load and length-to-diameter ratio from Figure 13a and check the minimum water film thickness according to Figure 12c. Figure 13b shows that the curvature radius of the journal center locus increases as L/D increases.

4.4. Effect of Relative Clearance on Bearing Performance

Figure 14 shows the water film pressure distribution, the bush deformation distribution and water film thickness distribution of rubber-plastic double-layer water-lubricated bearing for different relative clearances. The rotational speed is set to 1500 r/min, the relative clearance ranges from 0.1% to 0.4%, and the other parameters are the same as those in Table 1. Figure 15 shows the effect of the relative clearance on bearing lubrication performance for different eccentricity ratios. As the relative clearance increases, the water film thickness increases, the hydrodynamic pressure decreases, and the load-carrying capacity, friction torque and the maximum bush deformation are reduced. The actual minimum film thickness is the sum of Rψ(1 − ε) and bush deformation. When the relative clearance is small, the minimum water film thickness is small, the bush deformation is large, and the bearing lubrication performance is greatly affected by the bush deformation. As shown in Figure 15b, when the eccentricity ratio is 0.9 and the relative clearance is less than 0.2%, the bush deformation is much larger than the minimum film thickness value calculated by the formula Rψ(1 − ε). Figure 15c shows that the minimum film thickness decreases as the relative clearance increases from 0.1% to 0.15% for ε = 0.9. This is because the reduction of the bush deformation is greater than the increase in Rψ(1 − ε). The attitude angle changes little with the relative clearance. Figure 16 shows the variation curve of W to ε and the dimensionless journal center locus for different relative clearances. Designers can obtain the eccentricity ratio according to the load and relative clearance from Figure 16a and check the minimum water film thickness according to Figure 15c. Figure 16b shows that the curvature radius of the journal center locus decreases as the relative clearance increases.

4.5. Effect of Plastic Layer Elastic Modulus on Bearing Performance

Figure 17 shows the water film pressure distribution, bush deformation distribution and water film thickness distribution of rubber-plastic double-layer bearing for different elastic modulus of plastic layer bush, E₁. The relative clearance is set to 0.2%; the rotational speed is 1500 r/min; E₁ ranges from 100 MPa to 1300 MPa; and the other parameters are the same to those in Table 1. As E₁ increases, the bush deformation decreases, and the deformation distribution curve becomes smoother. The effect of E₁ on the water film thickness distribution and pressure distribution is limited, and the change mainly occurs at the loading area. Figure 18 shows the effect of E₁ on bearing lubrication performance for different eccentricity ratios. As E₁ increases from 100 MPa to 1300 MPa, the maximum bush deformation decreases by about 1 μm for ε = 0.4 and 6 μm for ε = 0.9. The decrease in bush deformation is small relative to the minimum film thickness; thus, E₁ has little effect on the minimum water film thickness. Only when ε is larger than 0.8, and E₁ is less than 500 MPa, the minimum water film thickness decreases significantly with the increase in E₁. The maximum pressure is affected by the minimum water film thickness. When the water film thickness decreases, the maximum pressure increases. The load-carrying capacity has the same changing rule with the maximum pressure. The friction torque and attitude angle increase slightly with E₁. Figure 19 shows the variation curve of W to ε and dimensionless journal center locus for different E₁. Figure 19a shows that when the eccentricity ratio is less than 0.8, E₁ has little influence on the load-carrying capacity. When the eccentricity ratio is larger than 0.8, and E₁ is larger than 300 MPa, E₁ has little influence on the load-carrying capacity. Figure 19b shows that the curvature radius of the journal center locus increases slightly as E₁ increases.

4.6. Effect of Plastic Layer Thickness on Bearing Performance

Figure 20 shows the water film pressure distribution, the bush deformation distribution and the water film thickness distribution of rubber-plastic double-layer water-lubricated bearing for different plastic layer thicknesses. The relative clearance is set to 0.2%, the rotational speed is 1500 r/min, and the total bearing bush thickness t is 10 mm. The plastic layer thickness t₁ increases from 3 mm to 7 mm, and the rubber layer thickness t₂ decreases from 7 mm to 3 mm. The other parameters are the same as those in Table 1. As t₁ increases, the bush deformation decreases. The change of bush deformation mainly affects the peak pressure value, and it has little effect on the water film thickness and pressure distribution. Figure 21 shows the effect of plastic layer thickness on bearing lubrication performance for different eccentricity ratios. It shows that as t₁ increases from 3 mm to 7 mm, the maximum bush deformation decreases by about 3.5 μm for ε = 0.4 and 8.5 μm for ε = 0.9. The decrease in bush deformation is small relative to the minimum film thickness, thus the thickness distribution of the double-layer bush has a limited effect on the minimum water film thickness. Only when the eccentricity ratio is larger than 0.8 does the minimum water film thickness decrease significantly as t₁ increases. As the water film thickness decreases, the maximum pressure increases. The load-carrying capacity has the same changing rule with the maximum pressure. The friction torque increases slightly with t₁. The attitude angle changes little. Figure 22a shows that when the eccentricity ratio is less than 0.8, t₁ has little effect on the load-carrying capacity. When the eccentricity ratio is greater than 0.8, and t₁ is more than 6 mm, t₁ has little effect on the load-carrying capacity. Figure 22b shows that the plastic layer thickness has little effect on the journal center locus.

5. Conclusions

This study established a fluid-structure coupling numerical calculation model for investigation of lubrication performance of the rubber-plastic double-layer water-lubricated journal bearings. The influence of eccentricity ratio ε, rotational speed N, length-to-diameter ratio L/D, relative clearance ψ, elastic modulus E₁ and thickness t₁ of the plastic layer bush on the bearing lubrication performance were studied. From the results, the following conclusions are drawn:

(1)

The bush deformation of the rubber-plastic double-layer bearing is between those of the rubber bearing and the plastic bearing, and its distribution area is close to that of the rubber bearing. However, the shape change of the double-layer bearing is smaller than that of the rubber bearing due to the larger stiffness of the plastic layer bush.

(2)

The maximum pressure, the maximum bush deformation, the load-carrying capacity and friction torque increase noticeably with N, and the variation increases with ε. The load-carrying capacity increases almost linearly with N for small ε values. When ε is more than 0.8, the influence of bush deformation on the minimum water film thickness becomes more significant, and the increase in load-carrying capacity with N slows down.

(3)

Under the influence of side leakage, the maximum water film pressure increases significantly with L/D for small L/D values, but as L/D increases, the maximum pressure increases to a certain value. L/D affects the load-carrying capacity and friction torque significantly.

(4)

With the increase in ψ, the load-carrying capacity and frictional torque decrease, the maximum bush deformation decreases, and the attitude angle has little changes. The bearing lubrication performance is greatly affected by the bush deformation for small ψ values.

(5)

The elastic modulus and thickness of the plastic layer bush mainly affect the bearing lubrication performance under heavy load conditions (ε > 0.8). As E₁ and t₁ increase, the maximum bush deformation and the minimum water film thickness decrease, and the load-carrying capacity increase. The friction torque and the attitude angle change little.

(6)

The data provided in Figure 9 and Figure 10, Figure 12 and Figure 13, Figure 15 and Figure 16, Figure 18 and Figure 19, Figure 21 and Figure 22 can be used for rapid structure design of this type of bearing.

The research results provide a theoretical basis for the structural design and application of rubber-plastic double-layer water-lubricated journal bearings. The static and dynamic characteristics of the bearings will be studied experimentally in future work.