Three-Dimensional DEM Modelling of Ball Bearing with Lubrication Regime Prediction
Abstract
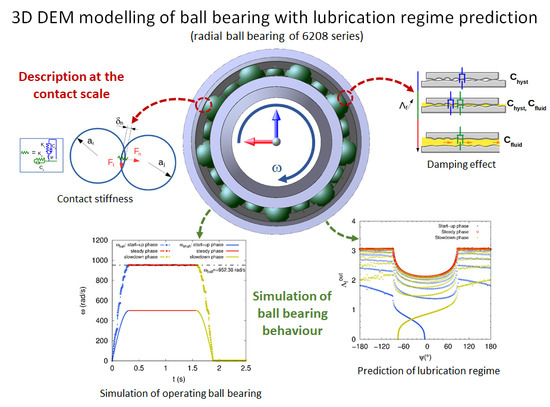
:1. Introduction
2. Three Dimensional Modelling of Radial Ball Bearing Using DEM
2.1. Contact Stiffness and Damping Effect
2.2. Fluid Film Thickness and Fluid Parameters
2.3. Space and Time Discretization of the DEM Ball Bearing Model
3. Numerical Prediction of Lubrication Regimes in Operating Radial Ball Bearing
3.1. Effect of Radial Load and Diametral Clearance
3.2. Effect of Angular Speed
4. Conclusions and Perspectives
Author Contributions
Acknowledgments
Conflicts of Interest
Nomenclature
| αe | Restitution coefficient of steel |
| δr | Radial shift |
| δn,t | Normal/tangential relative displacement |
| η | Dynamic viscosity of the fluid |
| Λf | Fluid number |
| μ | Friction coefficient |
| v | Poisson’s ratio of steel |
| w | Shaft/inner-ring angular speed |
| Approximate elliptic integral of second kind | |
| Approximate elliptic integral of first kind | |
| ψ | Azimuth angle |
| δa1,2 | Roughness parameter |
| ε | Load parameter |
| ξ | Viscosity-pressure coefficient of the lubricant |
| a | Restitution coefficient of steel |
| Cn,t | Normal/tangential viscous damping coefficient |
| E | Young’s modulus of steel |
| E′ | Effective elastic modulus of steel |
| Fr | Applied radial load |
| G | Shear modulus of steel |
| hmin | Semi-major axis of the Hertz’s elliptical contact |
| Jr | Radial integral |
| k | Ellipticity parameter |
| Kn,t | Contact normal/tangential stiffness |
| Pd | Diametral clearance |
| Qmax | Maximum normal load at ψ = 0 |
| Rb | Rolling element radius |
| Rc | Curvature radius of inner/outer raceway |
| Ri | Inner ring radius |
| Ro | Outer ring radius |
| Rz | Cage element radius |
| Rcurve | Curvature sum radius |
| Ur | Rolling velocity |
| vt | Sliding velocity |
| Z | Number of rolling elements |
Appendix A. Normal Load and Radial Deflection in Radial Ball Bearing


References
- Sapietová, A.; Dekýǎ, V. Dynamic analysis of rotating machines in MSC.ADAMS. Procedia Eng. 2016, 136, 143–149. [Google Scholar] [CrossRef]
- Zezulka, F.; Marcon, P.; Vesely, I.; Sajdl, O. Industry 4.0—An Introduction in the phenomenon. IFAC-Pap. Online 2016, 49, 8–12. [Google Scholar] [CrossRef]
- Ahuett-Garza, H.; Kurfess, T. A brief discussion on the trends of habilitating technologies for Industry 4.0 and Smart manufacturing. Manuf. Lett. 2018. [Google Scholar] [CrossRef]
- Chen, J.; Randall, R.B. Intelligent diagnosis of bearing knock faults in internal combustion engines using vibration simulation. Mech. Mach. Theory 2016, 104, 161–176. [Google Scholar] [CrossRef]
- Glowacz, A.; Glowacz, W.; Glowacz, Z.; Kozik, J. Early fault diagnosis of bearing and stator faults of the single-phase induction motor using acoustic signals. Measurement 2018, 113, 1–9. [Google Scholar] [CrossRef]
- Kompella, K.D.; Rao, M.V.G.; Rao, R.S. Bearing fault detection in a 3 phase induction motor using stator current frequency spectral subtraction with various wavelet decomposition techniques. Ain Shams Eng. J. 2017. [Google Scholar] [CrossRef]
- Júnior, J.J.D.S.; de Farias Maribondo, J. Analysis of lubricating oils in shear friction tests using infrared thermography. Infrared Phys. Technol. 2018, 89, 291–298. [Google Scholar]
- Hamrock, B.; Dowson, D. Isothermal elastohydrodynamic lubrication of point contacts: Part 1-theoretical formulation. J. Tribol. 1976, 98, 223–228. [Google Scholar] [CrossRef]
- Hamrock, B.J.; Dowson, D. Ball Bearing Lubrication: Elastohydrodynamics of Elliptical Contacts; John Wiley & Sons Inc.: New York, NY, USA, 1981. [Google Scholar]
- Masjedi, M.; Khonsari, M. On the effect of surface roughness in point-contact EHL: Formulas for film thickness and asperity load. Tribol. Int. 2015, 82, 228–244. [Google Scholar] [CrossRef]
- Stribeck, R. Ball Bearings for Various Loads. Trans. ASME 1907, 29, 420–463. [Google Scholar]
- Downson, D.; Higginson, G.R. Elasto-Hydrodynamic Lubrication, 2nd ed.; Pergamon Press: Oxford, UK, 1977. [Google Scholar]
- Stachowiak, G.; Batchelor, A. Engineering Tribology, 3rd ed.; Elsevier: New York, NY, USA, 2005. [Google Scholar]
- Fernandes, C.M.; Marques, P.M.; Martins, R.C.; Seabra, J.H. Film thickness and traction curves of wind turbine gear oils. Tribol. Int. 2015, 86, 1–9. [Google Scholar] [CrossRef]
- Cousseau, T.; Graça, B.; Campos, A.; Seabra, J. Grease Aging Effects on Film Formation under Fully-Flooded and Starved Lubrication. Lubricants 2015, 3, 197–221. [Google Scholar] [CrossRef]
- Gonçalves, D.; Graça, B.; Campos, A.V.; Seabra, J. Film thickness and friction behaviour of thermally aged lubricating greases. Tribol. Int. 2016, 100, 231–241. [Google Scholar] [CrossRef]
- Gonçalves, D.; Vieira, A.; Carneiro, A.; Campos, A.V.; Seabra, J.H.O. Film Thickness and Friction Relationship in Grease Lubricated Rough Contacts. Lubricants 2017, 5, 34. [Google Scholar] [CrossRef]
- Machado, C.; Guessasma, M.; Bellenger, E. An improved 2D modeling of bearing based on DEM for predicting mechanical stresses in dynamic. Mech. Mach. Theory 2017, 113, 53–66. [Google Scholar] [CrossRef]
- Tadina, M.; Boltezar, M. Improved model of a ball bearing for the simulation of vibration signals due to faults during run-up. J. Sound Vib. 2011, 330, 4287–4301. [Google Scholar] [CrossRef]
- Machado, C.; Guessasma, M.; Bellenger, E. Electromechanical modeling by DEM for assessing internal ball bearing loading. Mech. Mach. Theory 2015, 92, 338–355. [Google Scholar] [CrossRef]
- Chevallier, E.; Bourny, V.; Bouzerar, B.; Fortin, J.; Durand-Drouhin, O.; Da Ros, V. Voltage noise across a metal/metal sliding contact as a probe of the surface state. J. Appl. Phys. 2014, 115, 1–10. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Martin, B.; Bettscheider, S.; Gachot, C.; Kliem, H.; Mücklich, F. Correlation between solid–solid contact ratios and lubrication regimes measured by a refined electrical resistivity circuit. Wear 2014, 320, 51–61. [Google Scholar] [CrossRef]
- Rosenkranz, A.; Heib, T.; Gachot, C.; Mücklich, F. Oil film lifetime and wear particle analysis of laser-patterned stainless steel surfaces. Wear 2015, 334–335, 1–12. [Google Scholar] [CrossRef]
- Randall, R.B.; Antoni, J. Rolling element bearing diagnostics—A tutorial. Mech. Syst. Signal Process. 2011, 25, 485–520. [Google Scholar] [CrossRef]
- Bourbatache, K.; Guessasma, M.; Bellenger, E.; Bourny, V.; Fortin, J. DEM ball bearing model and defect diagnosis by electrical measurement. Mech. Syst. Signal Process. 2013, 41, 98–112. [Google Scholar] [CrossRef]
- Machado, C.; Guessasma, M.; Bellenger, E.; Bourbatache, K.; Bourny, V.; Fortin, J. Diagnosis of faults in the bearings by electrical measures and numerical simulations. Mech. Ind. 2014, 15, 383–391. [Google Scholar] [CrossRef]
- Cundall, P.; Strack, O. A discrete numerical model for granular assemblies. Geotechnique 1979, 29, 47–65. [Google Scholar] [CrossRef]
- Thornton, C.; Randall, C.W. Application of theoretical contact mechanics to solid particle system simulation. Micromech. Granul. Mater. 1988, 20, 133–142. [Google Scholar]
- Farah, S.O.; Guessasma, M.; Bellenger, E.; Machado, C. A 3D modelling of ball bearings by DEM and predictive monitoring method using electrical measurements. In Proceedings of the 6th Algerian Congress of Mechanics, Constantine, Algeria, 21–23 November 2017. [Google Scholar]
- Walford, T.L.H.; Stone, B.J. The sources of damping in rolling element bearings under oscillating conditions. Inst. Mech. Eng. 1983, 197, 225–232. [Google Scholar] [CrossRef]
- Archard, J.F. Elastic deformation and the laws of friction. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1957, 243, 190–205. [Google Scholar] [CrossRef]
- Qian, W. Dynamic Simulation of Cylindrical Roller Bearings. Ph.D. Thesis, Technische Hochschule Aachen, Aachen, Germany, 2014. [Google Scholar]
- Archard, J.F.; Kirk, M.T. Lubrication at point contacts. Proc. R. Soc. Lond. A Math. Phys. Eng. Sci. 1962, 261, 532–550. [Google Scholar] [CrossRef]
- Hamrock, B.; Anderson, W. Rolling-Element Bearings; For Sale by the National Technical Information Service: Springfield, VA, USA, 1983. [Google Scholar]
- Mindlin, R.; Deresiewicz, H. Elastic spheres in contact under varying oblique force. ASME J. Appl. Mech. 1953, 20, 327–344. [Google Scholar]
- Hunt, K.H.; Crossley, F.R.E. Coefficient of restitution interpreted as damping in vibroimpact. J. Appl. Mech. 1975, 42, 440–445. [Google Scholar] [CrossRef]
- Harnoy, A. Bearing Design in Machinery: Engineering Tribology and Lubrication; Mechanical Engineering; CRC Press: Boca Raton, FL, USA, 2002. [Google Scholar]
- Mary, C.; Philippon, D.; Devaux, N.; Fillot, N.; Laurent, D.; Bair, S.; Vergne, P. Bridging high pressure rheology and film-forming capacity of polymer-base oil solutions in EHL. Tribol. Int. 2016, 93, 502–510. [Google Scholar] [CrossRef]
- Tallian, T.E. Paper 14: Rolling Contact Failure Control through Lubrication. Proc. Inst. Mech. Eng. Conf. Proc. 1967, 182, 205–236. [Google Scholar] [CrossRef]
- Qiu, M.; Chen, L.; Li, Y.; Yan, J. Bearing Tribology: Principles and Applications; Springer: Berlin/Heidelberg, Germany, 2016. [Google Scholar]
- Higashi, K.; Isa, H.; Kitagawa, T.; Onishi, T.; Ohashii, K. Real-Time Monitoring of the Superfinishing Process; Technical Report, NTN No. 82; NTN Corporation: Kyomachibori, Japan, 2014. [Google Scholar]
- Guegan, J.; Kadiric, A.; Gabelli, A.; Spikes, H. The Relationship Between Friction and Film Thickness in EHD Point Contacts in the Presence of Longitudinal Roughness. Tribol. Lett. 2016, 64, 33. [Google Scholar] [CrossRef]
- Laurentis, N.D.; Kadiric, A.; Lugt, P.; Cann, P. The influence of bearing grease composition on friction in rolling/sliding concentrated contacts. Tribol. Int. 2016, 94, 624–632. [Google Scholar] [CrossRef]
- Björling, M.; Habchi, W.; Bair, S.; Larsson, R.; Marklund, P. Towards the true prediction of EHL friction. Tribol. Int. 2013, 66, 19–26. [Google Scholar] [CrossRef]
- Harris, T.; Kotzalas, M. Advanced Concepts of Bearing Technology, 5th ed.; Rolling Bearing Analysis; Taylor and Francis: Abingdon, UK, 2006. [Google Scholar]
- Dowson, D.; Higginson, G. Elasto-Hydrodynamic Lubrication; International Series on Materials Science and Technology; Elsevier Ltd.: Amsterdam, The Netherlands, 1977. [Google Scholar]
- Hamrock, B.; Schmid, S.; Jacobson, B. Fundamentals of Fluid Film Lubrication; Mechanical Engineering Fundamentals of Fluid Film Lubrication; CRC Press: Boca Raton, FL, USA, 2004. [Google Scholar]
- Lugt, P. Grease Lubrication in Rolling Bearings; Tribology in Practice Series; Wiley: New York, NY, USA, 2012. [Google Scholar]












| Component | Ball | Inner Ring | Outer Ring | Raceway | Cage |
|---|---|---|---|---|---|
| Radius | |||||
| Dimension (mm) | 6.3 | 24.0 | 36.6 | 6.552 | 4.19 |
| ∈]1,3] | ∈]3,5] | ||
| high | moderate | low |
| Angular Speed | Lubrication Regime | |
|---|---|---|
| Inner Contact | Outer Contact | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Guessasma, M.; Machado, C. Three-Dimensional DEM Modelling of Ball Bearing with Lubrication Regime Prediction. Lubricants 2018, 6, 46. https://doi.org/10.3390/lubricants6020046
Guessasma M, Machado C. Three-Dimensional DEM Modelling of Ball Bearing with Lubrication Regime Prediction. Lubricants. 2018; 6(2):46. https://doi.org/10.3390/lubricants6020046
Chicago/Turabian StyleGuessasma, Mohamed, and Charles Machado. 2018. "Three-Dimensional DEM Modelling of Ball Bearing with Lubrication Regime Prediction" Lubricants 6, no. 2: 46. https://doi.org/10.3390/lubricants6020046
APA StyleGuessasma, M., & Machado, C. (2018). Three-Dimensional DEM Modelling of Ball Bearing with Lubrication Regime Prediction. Lubricants, 6(2), 46. https://doi.org/10.3390/lubricants6020046