Detailed Investigations on the Oil Flow in Dip-Lubricated Gearboxes by the Finite Volume CFD Method †
Abstract
:1. Introduction
2. Object of Investigation and Operating Conditions
2.1. FZG No-Load Power Loss Test Rig
2.2. Test Gears
2.3. Lubricants
2.4. Operating Conditions
2.5. Derivation of the Gear Churning Loss
3. Numerical Model
3.1. Governing Equations
3.2. Geometry and Mesh
3.3. Derivation of the Gear Churning Loss
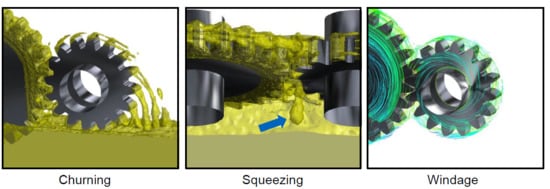
4. Results
4.1. Oil Distribution
4.2. Churning Power Loss
5. Conclusions
Supplementary Materials
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Concli, F. Efficiency of Gear Transmissions and CFD Analysis of the Load Independent Power Losses. Ph.D. Thesis, Politecnico di Milano, Milan, Italy, 2012. [Google Scholar]
- Mauz, W. Hydraulische Verluste von Stirnradgetrieben bei Umfangsgeschwindigkeiten bis 60 m/s. Ph.D. Thesis, Universität Stuttgart, Stuttgart, Germany, 1987. [Google Scholar]
- Strasser, D. Einfluss des Zahnflanken- und Zahnkopfspiels auf die Leerlaufverlustleistung von Zahnradgetrieben. Ph.D. Thesis, Universität Bochum, Bochum, Germany, 2005. [Google Scholar]
- Walter, P.; Langenbeck, K.; Dittrich, O. FVA-Nr. 44/I. Heft 118 Anwendungsgrenzen für die Tauchschmierung von Zahnradgetrieben, Plansch- und Quetschverluste bei Tauchschmierung; FVA: Frankfurt/Main, Germany, 1982. [Google Scholar]
- Liu, H.; Jurkschat, T.; Lohner, T.; Stahl, K. Determination of oil distribution and churning power loss of gearboxes by finite volume CFD method. Tribol. Int. 2017, 109, 346–354. [Google Scholar] [CrossRef]
- Doleschel, A. Wirkungsgradberechnung von Zahnradgetrieben in Abhängigkeit vom Schmierstoff. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2002. [Google Scholar]
- Leprince, G.; Changenet, C.; Ville, F.; Velex, P.; Jarnias, F. Influence of oil aeration on churning losses. In Proceedings of the JSME International Conference on Motion and Power Transmissions, Sendai, Japan, 13–15 May 2009. [Google Scholar] [CrossRef]
- Otto, H.-P. Flank Load Carrying Capacity and Power Loss Reduction by Minimised Lubrication. Ph.D. Thesis, Technical University of Munich, Munich, Germany, 2009. [Google Scholar]
- Li, L.; Versteeg, K.; Hargrave, G.K.; Potter, T.; Halse, C. Numerical Investigation on Fluid Flow of Gear Lubrication. SAE Int. J. Fuels Lubr. 2009, 1, 1056–1062. [Google Scholar] [CrossRef] [Green Version]
- Jafarian, P. Gear interlocking effect study using CFD. In Proceedings of the 3rd International CTI Symposium “Automotive Transmissions, HEV & EV Drives”, Berlin, Germany, 8–11 December 2014. [Google Scholar]
- Klier, C.; Berger, L. New prospects for oil flow simulation in rotating spur-gear systems. In Proceedings of the International Conference on Gears 2015, Garching b. München, Germany, 5–7 October 2015. [Google Scholar]
- Concli, F. Low-loss gears for precision planetary gearboxes. Influence of the gear design on the meshing and the churning power losses. In Proceedings of the International Conference on Gears 2015, Garching b. München, Germany, 5–7 October 2015. [Google Scholar] [CrossRef]
- Concli, F. Gearbox efficiency: The role of CFD. In Summer School Summer School 2016; Politecnico di Milano, Technical University of Munich: Milan, Italy, 2016. [Google Scholar]
- Concli, F. Numerical modelling of the churning power losses of gears: An innovative 3D computational tool suitable for planetary gearbox simulation. Tribol. Int. 2016, 103, 58–68. [Google Scholar] [CrossRef]
- Concli, F.; Gorla, C. CFD Simulations of windage losses of a gearbox. In Proceedings of the International CAE Conference 2012, Verona, Italy, 22–23 October 2012. [Google Scholar]
- Concli, F.; Gorla, C. Numerical modeling of the power losses in geared transmissions: Windage, churing and cavitation simulations with a new integrated approach that drastically reduces the computational effort. Tribol. Int. 2016, 103, 58–68. [Google Scholar] [CrossRef]
- Burberi, E.; Fondelli, T.; Andreini, A.; Facchini, B.; Cipolla, L. CFD Simulations of a Meshing Gear Pair. In Proceedings of the ASME Turbo Expo 2016: Turbomachinery Technical Conference and Exposition, Seoul, Korea, 13–17 June 2016. [Google Scholar]
- Gorla, C.; Concli, F.; Stahl, K.; Höhn, B.-R.; Michaelis, K.; Schultheiß, H.; Stemplinger, J.-P. CFD Simulations of Splash Losses of a Gearbox. Adv. Tribol. 2012, 2012, 616923. [Google Scholar] [CrossRef]
- Lucy, L.B. A numerical approach to the testing of the fission hypothesis. Astron. J. 1977, 82, 1013–1024. [Google Scholar] [CrossRef]
- Liu, H.; Arfaoui, G.; Stanic, M.; Montigny, L.; Jurkschat, T.; Lohner, T.; Stahl, K. Numerical Modelling of Oil Distribution and Churning Gear Power Losses of Gearboxes by Smoothed Particle Hydrodynamics. J. Eng. Tribol. 2017. [Google Scholar] [CrossRef]
- Iino, T.; Matsumura, S.; Houjoh, H.; Hachiya, T. Calculation of the behavior of oil churning and its loss in a gear box by a moving particle method—The first result of both calculation and experiment. In Proceedings of the International Conference on Power Transmissions 2016, Chongqing, China, 16–20 October 2016. [Google Scholar]
- Groenenboom, P.H.L.; Mettichi, M.Z.; Gargouri, Y. Simulating Oil Flow for Gearbox Lubrication using Smoothed Particle Hydrodynamics. In Proceedings of the International Conference on Gears 2015, Garching b. München, Germany, 5–7 October 2015. [Google Scholar]
- Liu, H.; Jurkschat, T.; Lohner, T.; Stahl, K. Numerical modeling and validation of oil distribution and churning losses in gearboxes. In Proceedings of the 6th World Tribology Congress 2017, Beijing, China, 17–22 September 2017. [Google Scholar]







| Gear | a in mm | z1|2 | mn in mm | α in deg | x1|2 in mm | b1|2 in mm | da1|2 in mm |
|---|---|---|---|---|---|---|---|
| Pinion (1) | 91.5 | 16 | 4.5 | 20.0 | 0.182 | 14 | 82.5 |
| Wheel (2) | 24 | 0.171 | 118.4 |
| Parameter | Symbol | FVA3 | FVA2 | FVA4 |
|---|---|---|---|---|
| ISO VG | - | 100 | 32 | 460 |
| Density at 40 °C in kg/m3 | ρ (15 °C) | 864 | 855 | 882 |
| Kinematic viscosity at 40 °C in mm2/s | ν (40 °C) | 95 | 32 | 480 |
| Kinematic viscosity at 100 °C in mm2/s | ν (100 °C) | 10.7 | 5.4 | 31.5 |
| Pressure p in Bar | Lubricant | Oil Sump Temperature ϑOil in °C | Oil Fill Level in mm | Rotational Speed of Pinion n1 in rpm | Circumferential Speed at the Pitch Circle vt in m/s |
|---|---|---|---|---|---|
| 1 | FVA3 | 40 | 32.2 mm below the middle axis (immersion depth of 9 mm of pinion) | 240 | 0.9 |
| FVA2 | 360 | 1.4 | |||
| FVA4 | 540 | 2.1 | |||
| 2734 | 10.5 | ||||
| 4101 | 15.7 | ||||
| 5225 | 20.0 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, H.; Jurkschat, T.; Lohner, T.; Stahl, K. Detailed Investigations on the Oil Flow in Dip-Lubricated Gearboxes by the Finite Volume CFD Method. Lubricants 2018, 6, 47. https://doi.org/10.3390/lubricants6020047
Liu H, Jurkschat T, Lohner T, Stahl K. Detailed Investigations on the Oil Flow in Dip-Lubricated Gearboxes by the Finite Volume CFD Method. Lubricants. 2018; 6(2):47. https://doi.org/10.3390/lubricants6020047
Chicago/Turabian StyleLiu, Hua, Thomas Jurkschat, Thomas Lohner, and Karsten Stahl. 2018. "Detailed Investigations on the Oil Flow in Dip-Lubricated Gearboxes by the Finite Volume CFD Method" Lubricants 6, no. 2: 47. https://doi.org/10.3390/lubricants6020047
APA StyleLiu, H., Jurkschat, T., Lohner, T., & Stahl, K. (2018). Detailed Investigations on the Oil Flow in Dip-Lubricated Gearboxes by the Finite Volume CFD Method. Lubricants, 6(2), 47. https://doi.org/10.3390/lubricants6020047