1. Introduction
Friction is one of the oldest phenomena humankind has sought to control. The control of friction promises a higher energy efficiency for mechanical processes and working devices and thus has utmost economical relevance [
1]. In dry conditions, friction is the result of two main contributions: shearing and plowing [
2]. In the case of metals, shearing consists of the formation of junctions between asperities at the interface between two solids, their deformation and ultimately rupture during relative motion. The shear strength
τ best describes the mechanical stability of such junctions. While the contact between engineering surfaces consist of many such junctions, the development of atomic force microscopy (AFM) [
3] and friction force microscopy [
4] has enabled the investigation of single asperity contacts and their response to sliding, thus bridging the gap between macro-scale tribological measurements, and the microscopic scales, at which the governing mechanisms of friction and wear operate. Recently, we have measured the shear strength for different metallic partners in single asperity sliding contact by AFM [
5]. In agreement with the criterion proposed in Reference [
6], we observed that metallurgical compatibility between tribological partners results in more friction. Plowing, on the other hand, results from the indentation of a harder asperity into the surface of a softer body and its material displacement upon relative motion. According to Bowden and Tabor, losses resulting from plowing friction are best described by the coefficient of friction
µ [
2]. Thereby, Bowden and Tabor have suggested that
µ mostly depends on the geometry of the indenter. In Reference [
7], we have used AFM to determine the plowing coefficient friction for metals of different hardness in contact with a diamond-coated AFM-tip. We found that the plowing coefficient of friction is determined by the resistance of a metal to be plastically deformed, i.e., its hardness.
In many situations, friction losses are lowered by the use of liquid, mostly oil-based lubricants [
8]. Such lubricants can, however, not be used in specific applications such as in medical, space, or micro-/nano-mechanical applications. For these cases, two-dimensional solid lubricants, such as graphene, maybe an alternative. Several studies have demonstrated the efficiency of graphene to reduce friction and retard wear (see Reference [
9] and references therein). The lubrication of graphene and other two-dimensional solids has been attributed to their high in-plane strength and chemical inertness that result in a low shear strength [
9].
Alternatively, vibrations have been known to reduce friction effectively. As highlighted in Reference [
10], vibrations are known to loosen nuts from screws or to allow for additional tightening of nuts on bolts. Mechanical vibrations are also known to initiate the transition between a stick-slip motion to continuous sliding in granular materials and are expected to trigger dynamic earthquakes [
11,
12]. Besides, the effect of vibration has been used, for example, to reduce the friction coefficient and die stresses during metal strip drawing [
13], to reduce the forces in wires drawing (see Reference [
14] and references therein), or to reduce the tool torque and both traverse and axial forces during the friction stir-welding process [
15]. The pioneering work in Reference [
16] has shown how the coefficient of static friction between steel surfaces vanishes under the application of normal vibrations with different frequency- and amplitude-values. There, the authors discussed their observations based on vibration-induced breaking of frictional weld junctions and the reduction of the contact area. In the lubricated and unlubricated cases of metals friction under gravity loading, the author in Reference [
10] reported a reduction of friction by vibrations with accelerations comparable to the acceleration due to gravity. This effect was also discussed based on a reduction in the contact area. In Reference [
17], the author investigated the static and kinetic friction reduction as a function of both the amplitude and frequency of induced vibrations. The author found that static friction steeply decreased with the acceleration of the vibrations. In the case of kinetic friction, the author reported that the effect of vibration in reducing friction also depends on the vibration acceleration and that it decreases at high sliding velocity. In Reference [
14], the author investigated the effect of vibrations on kinetic friction. In this work, the authors observed a friction reduction only for tangential vibration with respect to the sliding direction. There also, the effect of vibration vanished as the sliding velocity became comparable with the oscillation velocity. In References [
18,
19], the authors investigated the effect of normal vibrations on the coefficients of friction between mild steel pins sliding on various surfaces, such as mild steel, polymer, and composite materials. In the range of investigated vibration amplitude (10 to 200 µm) and frequency (up to 500 Hz), the authors observed a linear decrease in the coefficient of friction with increasing amplitude and frequency. The authors explained these observations based on the momentary load reduction during vibration. While early investigations of the vibration effect on friction were qualitative, the authors in Reference [
20,
21] proposed an analytical model to describe the effect of normal vibrations on friction for both Hertzian contact and contacts between rough surfaces. In both cases, the model relies on a momentary load reduction during friction. Specifically, the authors express the friction reduction due to normal contract vibration as:
where
Ff is the friction force,
is the friction force in the absence of contact vibration,
A is the contact area,
A0 is the contact area in the absence of vibration,
Fn is the normal force, and
F~ is the modulation force arising from the contact oscillation. From this equation a power-law could thus be expected.
Also, the effect of tangential vibrations on friction has been studied and described based on models such as the Dahl, Dupont models (see References [
22,
23,
24,
25,
26]). Unlike the effect of normal vibration, the effect of tangential vibrations has been explained based on a change of magnitude or direction of the sliding velocity vector. While the effect of normal vibration on solid friction has been explained based on a reduction of the contact force and thus of the contact area, several friction models, such as the rate-and-state friction (RSF) model [
27,
28] and the microphysical model [
29] have been developed to describe natural and induced fault phenomena such as earthquake nucleation and rupture propagation. These models rely on a logarithmic dependence of friction on the sliding velocity [
30]. Similarly, the authors in Reference [
31] reported on the effect of vibration in decreasing the critical force to initiate slip and in increasing the average slip distance in granular media. There, the authors observed a logarithmic dependence on the vibration velocity for both cases.
Meanwhile, several groups of researchers investigated the effect of vibration on the friction of single asperity contacts by AFM [
32,
33,
34]. In Reference [
32], the authors applied ultrasonic vibration vertical to the sample surface while sliding a Si
3N
4 AFM-tip over a Si surface in ambient and observed a reduction of friction. The authors explained this reduction based on the stiffening effect of ultrasonic vibration on a liquid interfacial layer between tip and sample. In Reference [
33], the author reported on the ultrasonic-assisted AFM-manipulation of Sb nanoparticles on MoS
2 substrates, thus further evidencing the effect of vibration to reduce friction. At the atomic scale, the authors in Reference [
34] observed a transition from dissipative atomic stick-slip to superlubricity between a Si tip and single crystals of NaCl and KBr cleaved along their (100) plane in ultra-high vacuum (UHV) and air upon excitation of the tip-supporting cantilever to its first contact bending resonance. The authors defined a criterion α
cr = 1 − η
−1 for the transition from stick-slip motion to superlubricity, where
η is the ratio of the potential energy of the corrugated interface to the potential energy of the sliding single-asperity. The authors in Reference [
35] extended the investigation of the vibration effect to the transition from atomic stick-slip to superlubricity to lateral vibration. There, the authors measured friction between a Si tip sliding on a NaCl (100) surface in UHV as a function of the excitation voltage of the first contact torsional resonance of the tip-supporting cantilever. They observed that the friction force linearly decreased while increasing the oscillation amplitude until the regime of superlubricity set on at an amplitude value equal to the equal to the interatomic distance. More recently, the authors in Reference [
36] explained the effect of out-of-plane contact vibration on friction reduction based on a non-linear force–distance curve between the tip and sample as a result of the local interaction potential.
Ultrasonic contact vibrations are thus effective in reducing friction at different length scales and in different environments. In the investigations above, the role of vibration amplitude and its ratio to the corrugation length of a surface potential, of vibration frequency or oscillation velocity have been outlined. These have yielded different predictions of the friction as a function of the vibration amplitude and frequency. In this work, we investigate the effect of contact vibration on the friction of sliding single asperity contacts of different adhesion strengths over a wide range of load and vibration amplitude. Analogous to the RSF-model in geophysics or the Prandtl–Tomlinson model used to describe atomic friction, we observe a logarithmic dependence of friction with the velocity of the oscillation. We also observe a logarithmic dependence of friction on the ratio of the modulation force to the normal force. Thus it appears that both velocity of the oscilation and variation in the contact area cojonintly effect a reduction in friction.
2. Sample Preparation and Characterization
We purchased a polycrystalline cold-rolled platinum foil by Fischer Scientific Korea Ltd., Incheon, Korea, and annealed it in an Ar atmosphere at 1273 K for 30 min. As a second sample, we used a graphene-coated copper foil, which we purchased by Graphene Square, Seoul, Korea.
Figure 1 shows topography images of the sample surfaces recorded by contact-mode AFM using an AFM XE-100 (Park Instruments, Seoul, Korea) with soft cantilevers. After annealing, we observe that the platinum surface facetted, resulting in smooth terraces and surface steps of several nanometers in height. Interestingly, the so formed steps in
Figure 1a form right angles with each other. Surface faceting occurs to reduce the surface energy. For fcc metals, the lowest surface energy is for the (111)-orientation. We suggest that the observed right-angle span between crystallographic orientations of the type
. The mean-square roughness corresponding to the Pt surface in
Figure 1a is
Rq = 7.64 nm.
Figure 1b,c shows images of graphene-coated copper recorded over two distinct areas. In both images, we observe graphene folds, although more numerous in
Figure 1b. For both imaged surface areas, the mean square roughness is similar:
Rq = 0.88–0.89 nm.
Also, we used X-ray photoelectron spectroscopy (XPS) (K-Alpha
+ XPS system, manufactured by ThermoFischer Scientific, Waltham, MA, USA) to confirm the successful graphenization of copper.
Figure 2 shows typical spectrograms recorded on graphenized copper after slow cooling. We performed the XPS measurements shown in
Figure 2 with a monochromated AlKα source (1486.6 eV, 12 kV) and a spot size of 400 um. Each measurement consisted of a 10-fold scan repetition. Before loading in the vacuum chamber with a base pressure below 5 × 10
−9 mbar, our sample had been exposed to ambient conditions. The XPS system we used does not allow for heating the sample to be measured after its introduction in a vacuum. Instead, low energy and low current Ar
+-sputtering can be used to clean the sample surface before XPS measurements. The results shown in
Figure 2 were recorded without any Ar
+-sputtering so as not to damage graphene. Beside peaks corresponding to different copper orbitals and a clear C1s-peak, the XPS results exhibit a prominent O1s-peak at 533 eV that corresponds to adsorbed water [
37] as well as a weak O1s-peak corresponding to copper oxide. The observed C1s-peak is a convolution of a prominent sp2-contribution at 284.04 eV corresponding to graphene, and two weaker contributions corresponding to C–C bonds at 284.8 eV and C–O bond at 538.35 eV. The occurrence of a peak at 538.5 eV is in good agreement with previous observations made on polycrystalline graphite wetted with water [
37]. Furthermore, we attribute the occurrence of the C–C bonds contribution to adventitious carbon contamination.
3. Experimental Methods
We investigated the effect of contact vibrations on the wear-less friction of Pt and graphene-coated Cu in air (T = 293 K, relative humidity RH = 40%) by a combination of contact-resonance (CR)-AFM and friction force microscopy (FFM) using an AFM XE-100 manufactured by Park Instruments, Seoul, Rebuplic of Korea.
Figure 3a schematically illustrates the working principle of the instrument used in this work. In our experimental set-up the cantilever is mounted onto a piezoelectric z-scanner (in purple color) and can be excited into vibration by a piezoelectric shaker (in pink color). A particularity of our instrument is that the z-scanner is decoupled from the x,y-scanners, i.e., the sample is mounted onto a linearized x,y-piezoelectric stage (in light grey color). Both normal and lateral deflections of the cantilever are measured using an optical beam deflection method, where a laser beam is reflected by the cantilever onto a four-quadrant photodiode. The response time of the photodiode is small enough to resolve the vibration amplitude of the cantilever. We used AFM cantilevers with normal stiffness
Cn-values ranging from 0.1 to 0.5 N/m. Specifically, we selected a Pt-coated Si cantilever to measure the effect of contact vibration on a Pt surface (type CONTSC-Pt), to achieve an adhesive contact. For measurements on graphene-coated Cu, we used an Au-coated silicon cantilever (type CONTSC-Au) and a single-crystalline Si cantilever with a native surface oxide (type CONTSC) to achieve different amounts of adhesion. All cantilevers were manufactured by NanoSensors, Switzerland. For each cantilever used in this work, we calibrated the sensitivity of the AFM photodiode
S by recording a force–distance curve on the respective sample surfaces and by calculating the slope of the repulsive part of the curve. Subsequently, we determined the bending and torsion stiffness of each cantilever from its thermal noise vibration [
38]. We extracted the adhesion forces between our different contact partners from force–distance curves.
The friction measurements consisted of recording the lateral deflection signal of the AFM cantilever in both forward and backward directions of the
x-scanner.
Figure 3b illustrates our friction measurements. Upon sliding the tip perpendicular to the cantilever axis, friction forces acting on the tip force the cantilever in torsion with an angle
θ. Note that the sign of
θ depends on the scanning direction. The torsion of the angle by the angle
θ yields a lateral shift of the laser spot on the photodiode, which results in a lateral deflection signal. The lateral deflection signal
Vl is recorded in volt and is subsequently converted into units of force according to:
where
h, the tip height, was taken to be 12 µm, in agreement with the manufacturer’s data. We calculated the friction force according to:
where
FL,fwd, and
FL,bwd are the forward and backward images of the lateral force.
Figure 3c shows experimental friction loops recorded under the same normal force value
Fn = 8 nN with a SiO
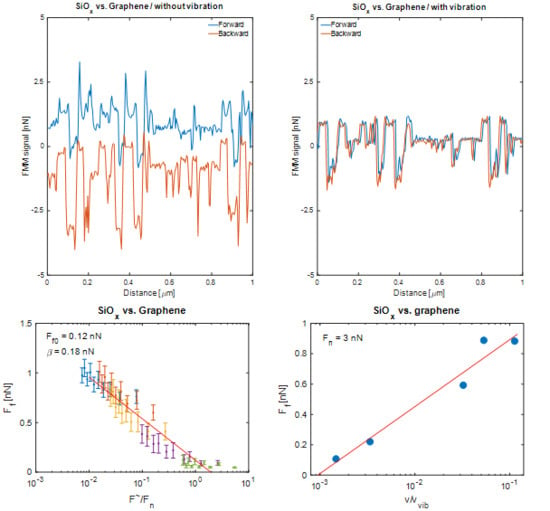
x AFM-tip on a graphenized copper surface with and without contact vibration. As indicated by Equation (3), the gap between the forward (in blue color) and the backward (in orange color) lines relates to the friction force. We averaged the calculated friction force image line-by-line and computed the corresponding error as the standard deviation from the mean value.
We investigated the effect of contact vibration by exciting the cantilevers into their first or second contact resonance. Thereby, we varied the piezoelectric excitation at the cantilever basis to achieve different resonance amplitude-values in the range of
A = 0–40 nm.
Figure 3 shows contact-resonance curves recorded on Pt with a Pt-coted tip with different excitation drive amplitude-values and under the action of a normal force
Fn = 2.5 nN. Also, we show the dependence of the resonance frequency
fr and the
Q-factor as a function of the amplitude for a Pt-tip in contact with Pt. We determined
fr and
Q by fitting a Lorentzian curve to each resonance curve. Except for the two lowest excitation drive amplitude values, we do not observe any significant change in
fr or the
Q-value. For the two smallest excitation drive amplitudes, the fit was as adequate as for the remaining resonance curves owing to a lower signal-to-noise ratio. For both curves with the lowest excitation drive amplitude values, the determination of
fr and
Q is, therefore, less accurate. Once the drive amplitude was selected and the contact vibration frequency set at the resonance value, we performed friction measurements with a sliding velocity
v = 8 µm/s over a scan area
As = 1 × 1 µm
2 and simultaneously recorded the vibration amplitude and phase as a function of
Fn.
Figure 3 also shows the variation of the contact vibration amplitude as a function of
Fn for different excitation drive amplitude values. In this graph, each amplitude value and its error correspond to the mean value and the standard deviation computed from a single amplitude image after averaging line-by-line. We observe slight variations of the vibration amplitude as a function of the normal force. According to Hertzian theory of elastic contact, the contact stiffness between a spherical body and a flat surface increases with the contact area
Ac as [
39]
Ac (
Fn) is the normal force-dependent area of contact between surface and tip, and
E* is the reduced modulus of elasticity (see References [
3,
4]). Several authors have shown how the contact resonance frequency of a cantilever
fr depends on
C* (see References [
40,
41]). For simplicity, we discuss this dependence in the frame of the first mode approximation (FMA) model [
41]. In this case, the first contact resonance frequency of a cantilever relates to the contact stiffness according to:
where
meff is an effective mass. From Equation (5), the contact resonance frequency increases with the contact stiffness, thus with the normal force. In this work, we set the contact vibration frequency at the resonance value for a normal force value
Fn = 2.5 nN. Variation in
Fn, however, yields a shift of the contact resonance frequency. In our case, the resonance frequency shift translated into a change in the measured contact vibration amplitude.
Furthermore, we determined a weighted shear strength
and the adhesion force
Fad by fitting the
-plots with the function:
where we consider
τ being a constant. In Equation (6) we used the Johnson–Kendall–Roberts (JKR) model to express the contact area as:
where
R is the tip radius [
42].
4. Results and Discussion
We measured the adhesion between three different tribological couples by recording force–distance curves. For a Pt-tip in contact with a Pt surface, we measured an adhesion force
Fad = 5.4 nN, for an Au-tip on graphene
Fad = 3.9 nN, and a SiO
x-tip on graphene
Fad = 1.4 nN. We attribute the higher adhesion force measured with a Pt-tip on Pt to the formation of a junction such as predicted by Bowden and Tabor [
2]. According to Rabinowicz, the mechanical strength of such junctions depends on the compatibility of the involved materials [
6]. The compatibility of materials can be deduced from their binary equilibrium phase diagram, where compatible materials are usually soluble in one another over a broad concentration range. As a particular case of compatible materials, identical materials can form a junction whose strength depends on the atomic bonding energy and the ductility of the material. Reciprocally, SiO
x and graphene are not compatible and thus exhibit a low adhesion force that might result from the capillary force exerted by a thin water film at the interface between the tip and sample. Au and graphene are not compatible either. In this case, too, we attribute the adhesion to capillary effects but explain the larger measured adhesion force value compared to SiO
x vs. graphene based on the larger Au-tip radius
Rtip. In agreement with our previous results, we set
Rtip = 25 nm for Au- and Pt-tips [
5,
43]. For the SiO
x-tip, we set
Rtip = 7 nm in agreement with the manufacturer’s data. The effect of water condensate on the adhesion and friction between hydrophilic and hydrophobic partners has been investigated in detail (see, for example, References [
44,
45,
46]). In an early study, the authors in Reference [
44] used bidirectional force microscopy to determine the effect of capillary condensation and humidity on friction and adhesion between a tungsten tip and a hydrophilic silicon surface, and less hydrophilic amorphous carbon and lubricated silicon oxide surfaces. The authors observed strong adhesion at high humidity in the case of the hydrophilic Si surface, but not on the less hydrophilic amorphous carbon and lubricated silicon oxide surfaces. The authors discussed these findings based on the strong capillary formation on hydrophilic surfaces and its suppression on less hydrophilic surfaces. Interestingly also, the authors observed that increasing humidity resulted in a decrease of the friction coefficient on silicon, while friction on amorphous carbon and lubricated silicon oxide was unaffected. This led the authors to suggest that the hydrophilicity of a surface promotes its aptitude to be lubricated by adsorbed water. In Reference [
45], the author presented similar results about friction on silicon with hydrophobic and hydrophilic tips as a function of humidity. The author found almost no effect of humidity on adhesion and friction between a hydrophilic AFM tip sliding on silicon. In the case of a hydrophilic tip sliding on silicon, however, the authors reported a significant decrease of friction and adhesion forces at high humidity values (>25%). The author discussed their observations based on the meniscus force and its kinetics during sliding contact. Moreover, in Reference [
46], the authors investigated the meniscus kinetics and its effect on nano-scale friction between a silicon nitride AFM tip and surface with different degrees of hydrophilicity. As in Reference [
44], the authors reported that an adsorbed water film on a hydrophilic surface acts as a lubricant at high humidity values. Further, the authors showed that friction on a hydrophobic surface is governed by thermally induced stick-slip.
We present our experimental friction results in
Figure 4. For all contact partners, i.e., Pt vs. Pt, Au vs. graphene, and SiO
x vs. graphene. For all three tribological couples, we show
Ff (
Fn) plots recorded under the action of different modulation force values
, where
A is the vibration amplitude. The values for
F~ ranged from 0 to 8 nN in the case of Pt vs. Pt, 0 nN to 6 nN for Au vs. graphene, and 0 nN to 3 nN for SiO
x vs. graphene. We combined Equations (6) and (7) to fit each
Ff (
Fn) plot and extract their
- and
Fad-values as a function of
F~. For all tribological couples, we observe a significant decrease in
Ff with increasing
F~ values. In most of all cases,
Ff (
Fn) plots acquired with a larger
F~ value lay under
Ff (
Fn) plots recorded with lower
F~-values. Also, the steepness of
Ff (
Fn) plots decreases with increasing
F~-values. In all cases, the fit quality was good, and we determined the corresponding confidence factor
R2 > 0.86. Equation (6) was initially proposed to describe the shearing friction of metals by Bowden and Tabor, in which case single asperities at surfaces may form a junction under the action of high local contact pressure, such as in cold welding. There the shear strength
τ describes the mechanical resistance of such a junction to plastic deformation and ultimately to rupture. It is interesting to see how this model also applies to tribological couples that do not directly form a junction, but rather adhere to each other under the effect of water capillary forces.
Table 1 summarizes the weighted shear strength
- and the adhesion force
Fad values for each tribological couple and different contact modulation force
F~ values. The adhesion force values determined from our experimental friction are, in all cases, smaller than the values we determined by recording force-distance curves. However, we do not observe any trend between the adhesion force and the contact modulation force. The fluctuations we observe for the adhesion force as a function of the modulation amplitude may result from tip changes and material transfer. In this work, we normalize the shear strength by
. The reason for this choice is that in the case of graphene-coated samples, the reduced modulus of elasticity is not well defined. On the one hand, as a 2-dimensional material, graphene does, by definition, not have a modulus of elasticity since such a modulus represents the capacity of a material to store elastic energy per unit volume. On the other hand, owing to its high stiffness, graphene is likely to enhance the elastic properties of the sample surface it is coated on. The stiffening effect of graphene on elastic contacts is difficult to determine and beyond the scope of this work. For all contact partners, we observe that contact modulation forces effectively decreased the value of the weighted shear strength. In the case of Pt vs. Pt, the weighted shear strength decreased from 70 to 10 Pa
1/3 while increasing the contact modulation force from 0 nN to 4 nN. For a Pt indenter in contact with Pt, the reduced elasticity modulus is
= 98.17 GPa (with the Young’s modulus
EPt = 168 GPa and and the Poisson’s ratio ν
Pt = 0.38). Consequently, we find that in the same range of contact modulation force-values, the shear strength decreased from
τ = 1.485 GPa to
τ = 214.5 MPa. In Reference [
47], the authors evaluated the ultimate tensile strength of Pt-thin films to
σu = 1.8 GPa. According to Reference [
48], the shear strength is typically a factor 1.66 smaller than the ultimate tensile strength. Our result
τ is larger than reported in Reference [
47]. We attribute this difference to the fact that we annealed Pt at 1000 °C. Consequently, we expect its dislocation density to be low and its mechanical strength to be higher than reported in Reference [
47]. For the largest
F~ value, though the value of the weighted shear strength increased again to 24 Pa
1/3.
In the case of Au vs. graphene, we observe a monotonous decrease in the weighted shear strength from 19 to 3.42 Pa1/3 in the range of F~ = 0–5 nN. Similarly, the weighted shear strength of the SiOx/graphene tribological couple decreases from 16 to 1 Pa1/3 while increasing F~ from 0 to 3 nN. Without a clear distinction between the values of the reduced modulus of elasticity for Au vs. graphene and SiOx vs. graphene it remains, however, difficult, to explain the observed difference in their -values.
It is thus evident that contact vibrations reduce friction. Beyond confirming results in References [
10,
11,
12,
13,
14,
15,
16,
17,
18,
19,
20,
21,
27,
28,
29], we further show in
Figure 5c how the friction force logarithmically relates to the ratio of the contact modulation force to the normal force. For all three tribological partners investigated in this work, we observe that
Ff decreases while increasing
F~/
Fn, according to:
The values we determined for Ff0 follow a similar trend as the weighted shear strength, i.e., Ff0 is high when is heigh, and reversely. Furthermore, we find following β-values: β = 0.45 nN for Pt vs. Pt and Au vs. graphene and β = 0.18 nN for SiOx vs. graphene. In our experiments, the contact resonance frequency was fr = 175 kHz for Pt vs. Pt, fr = 150 kHz for Au vs. graphene, and fr = 175 kHz for SiOx vs. graphene. Thus it is not possible to establish a dependence of the friction force on the contact vibration frequency.
A logarithmic dependence between friction and the sliding velocity has been observed for single asperity contacts and discussed based on the Prandtl–Tomlinson model. In this model, a single asperity mounted on a spring and being sled over a corrugated potential energy landscape gives rise to atomic stick-slip tip motion [
49]. According to this model, the velocity and temperature dependence of friction is expressed as:
where
Ff0 is the friction at 0 K,
kB is the Boltzmann constant,
a is the interatomic distance, and
where
f0 is the natural frequency of the spring-coupled single asperity, and
C is the stiffness of the spring. In analogy to this model, we plot the friction
Ff as a function of the ratio of the sliding velocity
v to the vibration velocity
. We find that the friction force also follows a logarithmic dependence with the ratio
v/
vvibFigure 6 shows the relationship between friction and the
v/
vvib – ratio for a selected normal force value
Fn = 3 nN and the three tribological couples investigated in this work. In all cases, a logarithmic dependence is observed. Also shown in this figure is the dependence of the extracted
Ff0- and
β-parameters obtained by fitting Equation (11) to our experimental data. As in
Figure 4, we fitted Equations (6) and (7) to the
Ff0(
Fn) plots. For Pt vs. Pt, we determined
Fad0 = 1.06 nN and
= 112.04 Pa
1/3, Au vs. graphene
Fad0 = 0.32 nN and
= 34.45 Pa
1/3, for SiO
x vs. graphene
Fad0 = 0.24 nN and
= 26 Pa
1/3. In all cases, we thus infer that
τ0 is almost a factor 2 larger than for the smallest vibration amplitudes. Analog to Equation (8), we identify
τ0 with the shear strength at 0 K. For Pt vs. Pt,
β linearly increases from 0.34 to 0.73 nN in the range of normal force values F
n = 0.33–4.85 nN. For Au vs. graphene,
β slightly increases from 0.35 to 0.6 nN in the range of F
n = 0–16.58 nN. For SiO
x vs. graphene,
β ≈ 0.2 nN in the range of
Fn = 0–5 nN. Identifying
β with the pre-logarithmic factor in Equation (9), and assuming that the corrugation length is in our case
l =
v/
fr we find that the energy term
= 0.5 × 10
−20–1.6 × 10
−20 J, while at
T = 300 K the thermal energy is
Eth = 0.4 × 10
−20 J. We suggest that the effect of contact vibration is analogous to the case of atomic stick-slip, where both thermal energy and the energy stored in the tip mediate a jump over the barrier between two local minima of the potential landscape. Contact vibrations both result in the corrugation of a surface-energy landscape and the tuning of the tip-oscillation velocity, i.e., the attempt rate of jumps of the corrugation barrier.