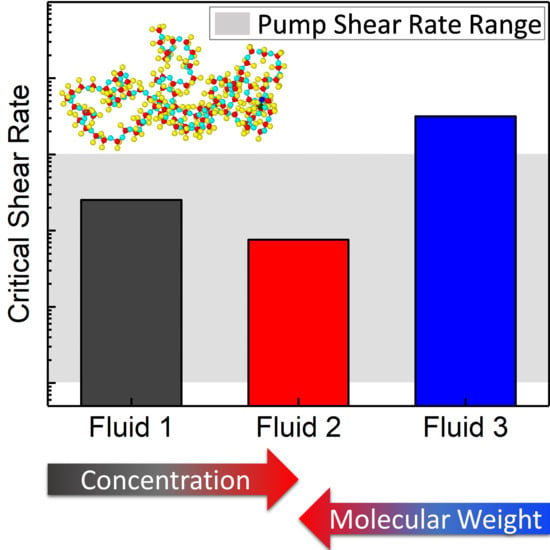
Critical Shear Rate of Polymer-Enhanced Hydraulic Fluids

Abstract

Many application-relevant fluids exhibit shear thinning, where viscosity decreases with shear rate above some critical shear rate. For hydraulic fluids formulated with polymeric additives, the critical shear rate is a function of the molecular weight and concentration of the polymers. Here we present a model for predicting the critical shear rate and Newtonian viscosity of fluids, with the goal of identifying a fluid that shear thins in a specific range relevant to hydraulic pumps. The model is applied to predict the properties of fluids comprising polyisobutene polymer and polyalphaolefin base oil. The theoretical predictions are validated by comparison to viscosities obtained from experimental measurements and molecular dynamics simulations across many decades of shear rates. Results demonstrate that the molecular weight of the polymer plays a key role in determining the critical shear rate, whereas the concentration of polymer primarily affects the Newtonian viscosity. The simulations are further used to show the molecular origins of shear thinning and critical shear rate. The atomistic simulations and simple model developed in this work can ultimately be used to formulate polymer-enhanced fluids with ideal shear thinning profiles that maximize the efficiency of hydraulic systems.

1. Introduction

Hydraulic systems function and perform tasks through a pressurized fluid, which is controlled directly or automatically by control valves, distributed through hoses, displaced by pumps, and actuated by cylinders and motors. The efficiency of hydraulic power transmission is primarily affected by internal leakage flow in pumps and motors and by friction and viscous drag in pumps, motors, and cylinders. These losses generate heat and reduce the power available to engage the payload [1,2]. The overall efficiency of hydraulic machines can therefore be separated into two components: volumetric efficiency associated with internal leakage, and mechanical efficiency due to frictional losses. The product of the volumetric and mechanical efficiencies is the overall efficiency of a hydraulic system or component such as a pump or motor [2].

Both volumetric and mechanical efficiency depend on the viscosity of the hydraulic fluid, since the fluid functions as both lubricant and power transmission medium. However, fluid viscosity has opposite effects on the two types of efficiency. Specifically, volumetric efficiency increases with increasing viscosity because thicker fluids leak less; in contrast, mechanical efficiency decreases with increasing viscosity because thicker fluids exhibit higher viscous friction and drag. Therefore, the overall efficiency of hydraulic systems varies with fluid viscosity non-monotonically [2,3,4,5,6,7].

The effect of fluid viscosity on efficiency is further complicated by the fact that viscosity itself depends on operating conditions. Notably, the viscosity of hydraulic fluids decreases rapidly as system temperature increases [8], an effect that is more significant in applications with small oil reservoirs and compact heat exchangers, which lead to higher operating temperatures. Because of this, many hydraulic fluids are formulated with viscosity modifiers (VMs) or viscosity index (VI) improvers to reduce the variation of viscosity during machine operation [9,10]. These additives are long-chain polymers that incorporate repeating molecular blocks of acrylate, olefin, styrene, ethylene, butylene, and alkyleneglycol monomers. Fluids with VMs flow easily at low temperatures and mitigate heat-related viscosity loss at high temperatures, improving the fluid’s performance as a lubricant at both low and high temperatures [11].

While VMs are needed for operation across a range of temperatures, they also change the rheological properties of fluids, introducing more complex viscosity behavior that is a function of shear stress. At low shear stress conditions, fluids are near their equilibrium state and have viscosity that is independent of shear rate (or stress), i.e., the Newtonian viscosity. However, the high shear stresses in lubricating gaps can cause reversible and nonreversible viscosity loss, also called shear thinning. Reversible, or temporary, viscosity loss occurs when polymers elongate and align with the shear plane but return to their original configuration when shear forces are removed. Irreversible, or permanent, viscosity loss results from mechanical scission of polymer molecules, resulting in lower molecular weight molecules [7,12]. Both types of shear thinning are functions of the concentration, size, and architecture of the polymer molecules [13,14,15,16,17,18].

Studies conducted on hydraulic fluids in a dynamometer have suggested that temporary viscosity loss occurs when the fluids are exposed to high shear rates in streamline flows, whereas permanent viscosity loss occurs when fluids are exposed to intense and prolonged shear rates under more extreme conditions [7,19]. Therefore, when formulating hydraulic fluids, VM polymers are chosen such that they do not mechanically degrade and form smaller, less effective polymer fragments when subjected to very high shear rates [11,20,21].

However, fluids will still experience temporary viscosity loss. In fact, even small molecules may exhibit shear thinning in the elastohydrodynamic lubrication regime because of progressive alignment of molecules with shear rate [22,23]. Rheological measurements of low molecular weight squalane in both the Newtonian and non-Newtonian regimes have suggested that shear thinning increases with increasing pressure and decreasing temperature [23]. Temporary shear thinning behavior is often described by models with power-law scaling of shear stress with shear rate [24]. Commonly used equations to capture this behavior in lubricants and hydraulic fluids are the Carreau, Cross, and Ree–Eyring models [24]. Such models predict that viscosity will be constant at low shear rates ($\eta ={\eta }_0$) and then decrease rapidly ($\eta =f\left(\dot{\gamma }\right)$) above some critical shear rate ${\dot{\gamma }}_{cr}$. The critical shear rate characterizes the transition from Newtonian to non-Newtonian (shear thinning) behavior. This critical value is usually taken to be the shear rate at which the tangent to the power law regime intersects with the Newtonian viscosity line [24].

The temporary shear thinning behavior described above presents an opportunity to tune the viscosity of hydraulic fluids. To maximize volumetric efficiency, high viscosity is required; the opposite is needed to maximize mechanical efficiency. For a fluid with VMs that exhibits shear thinning, both objectives could be achieved if the fluid is subject to low shear where flow loss is a concern and then subject to high shear where viscous friction is an issue. The challenge, however, is to (i) identify the range of shear rates relevant to hydraulic machines and (ii) formulate a hydraulic fluid that shear thins in this same range. In a previous study [25], we analyzed the operation of an axial piston pump and found the range of shear rates in key lubricating gaps within the pump to be between 10${}^4$ and 10${}^7$ 1/s. The efficiency of the pump with three different fluids was tested, but none was found to affect efficiency because their critical shear rate was above the range calculated for the pump. However, it was suggested that if a fluid were to be formulated with higher molecular weight VMs that are more susceptible to shear thinning in the critical shear rate range, shear thinning might be leveraged to optimize the efficiency [25]. The first step towards this goal is to identify a fluid with the desired shear thinning behavior.

The key parameter needed to tune shear thinning behavior is the critical shear rate. Critical shear rate ${\dot{\gamma }}_{cr}$ can be correlated to the inverse of the longest relaxation time for the molecules at equilibrium (i.e., in the absence of shear), which is expected to be the rotational relaxation time $\lambda$ for polymers [22,26,27,28,29,30,31]. The dynamics of polymers are typically described in terms of the Rouse [32,33] and reptation models [34,35,36]. The Rouse model provides an excellent description for the melt of short, unentangled polymer chains, while the dynamics of the long entangled chains can be described by the reptation model [26,35,37]. Hydraulic fluids are formulated with relatively short, unentangled polymer chains, so the Rouse model should be most applicable. In this model, the rotational relaxation time is given by $12{\eta }_{0}M/\left({\pi }^2\rho R_{g}T\right)$, where ${\eta }_0$ is the Newtonian viscosity of the liquid, M is molecular weight, $\rho$ is mass density, $R_g$ is the universal gas constant, and T is temperature. The relationship was corroborated by molecular dynamics (MD) simulations of linear polymers with 5 to 400 monomers that showed dependence of polymer dynamics on molecular weight consistent with the Rouse model [26]. Therefore, the Rouse equation can be used to predict the approximate relaxation time of a fluid based on the molecular weight of the polymer. However, the approach has not been extended to formulate fluids with desired relaxation times and acceptable Newtonian viscosity for hydraulic machines.

Here, we propose a model based on the Rouse equation that captures the effects of both the molecular weight and concentration of the polymer and the viscosity of the base oil to predict the formulation of a hydraulic fluid that shear thins at a predefined shear rate and with a desired Newtonian viscosity. A fluid was identified based on these predictions comprising polyisobutylene (PIB) polymers in polyalphaolefin (PAO) synthetic base oil. This fluid, along with two others with different polymer concentrations and molecular weights, were synthesized, characterized, and modeled using MD simulation. The critical shear rates predicted by the theoretical model were compared to rheological data across several decades of shear rates obtained from experiments and simulations. MD simulations were then used to explore the molecular origins of the shear thinning behavior. This study lays the groundwork for design of fluids with tunable viscosity behavior and optimized hydraulic efficiency.

2. Materials and Methods

2.1. Rheological Measurements

Two different instruments (see Figure S1) were used to characterize the rheological properties of the test fluids at 50 and 80 ${}^{\circ }$C in both the Newtonian and non-Newtonian regimes. First, a Cannon StressTech HR Oscillatory Rheometer was used to measure the dynamic viscosity of the fluids under low shear rate conditions. The shear rate was varied from 10 to 1000 1/s, with 15 measurements taken at logarithmically spaced intervals in that range. This procedure was repeated three times for each fluid to report average viscosity values at each shear rate and temperature. The standard deviation of the average of the three measurements was around ±0.2 mPa·s.

A PCS Ultra Shear viscometer was used to measure the high-shear viscosity at approximate shear rates from 300,000 to 4,000,000 1/s. Two repeat high-shear viscosity measurements were performed for one of the fluids and the difference was used to estimate a maximum error of 1.4 mPa·s. Measurements at the highest shear rates also exhibited a temperature rise up to 5 ${}^{\circ }$C above the set temperature (50 or 80 ${}^{\circ }$C). This may have resulted in artificially low viscosity measurements at the highest shear rates.

2.2. Molecular Dynamics Simulations

MD simulations were used to obtain the Newtonian viscosity, high-shear viscosity, and to understand the dynamics of the molecules during shear. The model systems were created using Material Studio software. All atomic interactions were described using a united atom (UA) potential. UA potentials are known to accurately describe the viscosity of hydrocarbons at ambient conditions and high pressures according to numerous past studies [23,27,28,38,39,40,41]. The UA parameters were selected from Transferable Potentials for Phase Equilibria (TraPPE-UA) developed for branched alkanes and alkenes [42,43,44,45]. Details about the UA potential and force field parameters are given in Section S2. Simulations using the TraPPE-UA force field were performed with a spherical cutoff of 1.4 nm and analytic tail corrections for the Lennard–Jones interactions. The bond length is not considered to be rigid but is controlled by a harmonic potential with the force constants taken from the CHARMM force field [45,46,47]. For all simulations, a time step of 1.0 fs was used and periodic boundary conditions were applied in all directions with a 4 × 4 × 30 nm simulation box. The box was longer in one direction to allow the molecules to elongate in response to shear in high-shear viscosity simulations without unphysical effects from the periodic boundary. Dynamic simulations were run using Large Atomic/Molecular Massively Parallel Simulation (LAMMPS) software [48].

To prepare the model system, an energy minimization of the system was performed using the conjugate gradient algorithm. The system density was then equilibrated at 1.0 atm and either 50 or 80 ${}^{\circ }$C for 50 ns in the isothermal–isobaric (NPT) ensemble using the Nosé–Hoover thermostat and barostat [49,50], with damping coefficients of 100 and 125 fs, respectively. Then, while maintaining a constant temperature for 10 ns in the canonical (NVT) ensemble, the simulation box was deformed until the density of the fluid reached the average density computed from the last 10 ns of the previous NPT simulations. Finally, the system was equilibrated using the final configuration from NVT as the initial configuration for 5 ns in the microcanonical (NVE) ensemble. This way, a desired equilibration state of the system was achieved while avoiding interference with the dynamics of the system [51]. Following this equilibration process, two sets of simulations, equilibrium and non-equilibrium, were carried out to calculate viscosity at 50 and 80 ${}^{\circ }$C. These temperatures were chosen to reflect the temperature range experienced by lubricants used as hydraulic fluids.

First, the Newtonian viscosity of fluids was modeled using equilibrium molecular dynamics (EMD). Specifically, we used the Green–Kubo (GK) approach, which relates the viscosity to the time integral of the stress autocorrelation function [51,52]; see Section S3 for details. Using the previously equilibrated model, simulations were equilibrated again for 2 ns in the NPT ensemble followed by NVE ensemble production runs. The pressure tensor components were saved every 5 fs for 5 ns at 50 ${}^{\circ }$C and 20 ns at 80 ${}^{\circ }$C during the NVE simulation. An average low-shear viscosity value was calculated from multiple NVE trajectories and by applying the GK formalism following the time decomposition approach [52].

Second, non-equilibrium molecular dynamics (NEMD) simulations were used to determine the viscosity at high shear rates and to study the non-Newtonian viscosity behavior. NEMD simulations for calculating viscosity involve applying a planar Couette flow field at shear rate $\dot{\gamma }=\partial u_x/\partial z$ to induce a flow gradient or momentum flux, and characterizing the linear change in streaming velocity of flow $u_x$ in the x-direction with vertical position z [23,53,54]. First, shear was imposed on the simulation box at a desired strain rate by deforming the box in the x-direction for 100–1000 ns, depending on the shear rate. At the same time, the fluids were thermostatted via a Nosé Hover thermostat and the SLLOD equations of motion. Depending on the shear rate, 10–200 ns of time was provided for the system to achieve steady-state before the shear stress $P_{xz}$ and velocities of the atoms in the direction of shear $u_x$ were collected for post processing. It was assumed that an NEMD simulation reached steady-state if the goodness of the slope of a linear fit to the average atom velocities was 99% or greater. The average shear rate was then calculated from the slope of a linear fit to the average atom velocities and average viscosity was determined from the ratio of the average shear stress to the average shear strain rate; see Section S3 for details. This process was repeated for each test fluid at 50 and 80 ${}^{\circ }$C for shear rates ranging from $1\times {10}^8$ to $1\times {10}^{11}$ 1/s.

3. Results and Discussion

3.1. Fluid Identification and Formulation

We considered blends of linear polyisobutylene (PIB) polymer and synthetic polyalphaolefin (PAO) base oil. The Newtonian viscosities and critical shear rates were calculated for fluids comprising 12, 16, or 20 wt.% PIB polymer at varying concentrations in PAO 2 mm${}^2$/s (PAO2), PAO 4 mm${}^2$/s (PAO4) or PAO 8 mm${}^2$/s (PAO8) base oil. The PAOs used here are representative of the viscosity grades of base stocks used in formulating hydraulic fluids that usually range from 2–8 mm${}^2$/s at 100 ${}^{\circ }$C, depending on the additives.

The Newtonian viscosity ${\eta }_0$ and density $\rho$ of the blend were predicted by the Kendall–Monroe relation [55] and the sum of the mass fractional density of each component, respectively, using the viscosities (${\eta }_{0p}$ and ${\eta }_{0s}$), densities (${\rho }_p$ and ${\rho }_s$), and concentrations ($c_p$ and $c_s$) of the polymer p and base oil solvent s. The Newtonian viscosity ${\eta }_{0p}$ of the polymers at 25 ${}^{\circ }$C as a function of molecular weight was calculated from an empirical model derived from a large set of experimental data [56]. The viscosity of the polymers at 25 ${}^{\circ }$C was then used to obtain viscosity at 80 ${}^{\circ }$C using the temperature shift factor for PIB [57] and the temperature dependence of viscosity described by the William–Landel–Ferry equation [57]; all equations are given in Section S4.

The critical shear rate was calculated using a model developed by combining the Rouse equation [28,33,58] for rotational relaxation time with the kinetic-theory-based rigid dumbbells model proposed by Bird et al. [24,59], which is similar to the Rouse model but includes polymer concentration and base oil viscosity terms; original equations given in Section S4. The proposed model correlates critical shear rate ${\gamma }_{cr}$ to the molecular weight M and concentration $c_p$ of the polymer, and the viscosity and density of the blend and base oil as

$${\gamma }_{cr}=1/\lambda =\frac{{\pi }^2}{12}\frac{c_p\rho R_{g}T}{({\eta }_0-{\eta }_{0s})M}$$

(1)

where $R_g$ is the universal gas constant and T is temperature. These models were originally derived based on the assumption that only a single molecular mass, in this case the polymer, contributed to the shear response of the blend. The same is true for this new model. For a liquid, shear thinning is said to occur when the Weissenberg number $Wi$, which is the product of the relaxation time $\lambda$ and shear rate $\dot{\gamma }$, is greater than unity (that is, $Wi=\lambda \dot{\gamma }>1$) [24]. This criterion was used with Equation (1) to estimate the critical shear rate for different combinations of commercially available PAO base oils and PIB polymers across a range of polymer concentrations.

Figure 1 shows the calculated critical shear rate and Newtonian viscosity of fluids comprising 12, 16, and 20 wt.% PIB polymer with PAO2, PAO4, or PAO8 base oil as a function of the molecular weight of the polymer. The critical shear rate decreases with both the molecular weight and concentration. However, the effect of polymer concentration on the critical shear rate is small relative to the effect of molecular weight. The Newtonian viscosity increases with molecular weight and concentration. Unlike critical shear rate, the effect of molecular weight is more significant than that of concentration. It can also be observed that a fluid blended with a lower viscosity base oil has a higher critical shear rate and lower Newtonian viscosity fluid.

The predictions in Figure 1 can be used to identify an ideal fluid formulation. Specifically, the target blend should have a Newtonian viscosity suitable for a hydraulic pump (8 to 10 mPa·s at 80 ${}^{\circ }$C) and critical shear rate in the range of shear rates exhibited in the key lubricating gaps within that pump (10${}^4$ to 10${}^7$ 1/s). The model predictions suggest that an ideal fluid formulation is 12 wt.% 6.0 kg/mol PIB in PAO4, identified by dashed lines and the star in Figure 1b. This blend should have a critical shear rate of $8.7\times {10}^6$ 1/s and Newtonian viscosity of 8.9 mPa·s at 80 ${}^{\circ }$C, both of which are within the desired range for the hydraulic pump.

Based on the outcomes of this analysis, we formulated a fluid blend (Fluid 1) from 12 wt.% 6.0 kg/mol PIB (PIB6000) polymer with 88 wt.% PAO4 base oil. Then, two additional fluids were designed to test the effects of concentration and molecular weight of the polymer on critical shear rate. Fluid 2 was formulated with 16 wt.% PIB6000 in PAO4 while Fluid 3 was formulated with 12 wt.% of 1.3 kg/mol polyisobutylene (PIB1300) polymer in PAO8 base oil. A summary of the formulation plan for these three fluids is given in

Table 1. Chemical composition of the test fluids.

Fluid ID	Fluid 1	Fluid 2	Fluid 3
PAO4	88 wt.%	84 wt.%	-
PAO8	-	-	88 wt.%
PIB1300	-	-	12 wt.%
PIB6000	12 wt.%	16 wt.%	-

. Fluids 1 and 2 have the same polymer and base oil, but different polymer concentration. Fluids 1 and 3 have the same polymer concentration, with different molecular weight polymer and PAO base oil. Apart from the polymer, no other additives were included in the fluid formulations.

The three fluids formulated above were modeled using MD simulations. Consistent with previous gas chromatography-mass spectroscopy measurements, PAO4 was modeled as equal parts 1-decene trimer and tetramer and PAO8 was modeled as 1-decene tetramer [60]. The PIB1300 polymer was built from 22 isobutylene monomers and an exo group so that the resulting molecule had a nominal molecular weight of 1300 g/mol and a bromine number of 12, indicating it was a linear olefin with one unsaturated bond (C${}_{96}$H${}_{192}$) [61]. Similarly, the PIB6000 polymer comprised 106 isobutylene monomers and an exo group so that the resulting molecule had a nominal molecular weight of 6000 g/mol and a bromine number of 3, indicating it was a linear olefin with one unsaturated bond (C${}_{428}$H${}_{856}$) [61]. The virtual models of the 1-decene molecules and PIB polymers are shown in Figure 2.

The three model fluid systems were created by placing base oil and polymer molecules in a periodic simulation box. The number of molecules was determined based on the percent weight concentrations in Table 1. Note that the number of molecules in each model system varied, but the size of the simulation box was kept approximately constant. A summary of the number of molecules in the model of each of the three fluids is reported in

Table 2. Simulation plan for the three fluids with the number of molecules of each type for each model.

Fluid ID	Fluid 1	Fluid 2	Fluid 3
Decene trimer, C${}_{30}$H${}_{62}$	261	244	-
Decene tetramer, C${}_{40}$H${}_{82}$	196	168	386
Polymer, PIB1300 (C${}_{96}$H${}_{192}$)	-	-	22
Polymer, PIB6000 (C${}_{428}$H${}_{856}$)	5	6	-

.

3.2. Rheological Behavior

The accuracy of the simulations was evaluated by comparing Newtonian viscosities obtained from the EMD simulations to measured values for the fluids. The Newtonian viscosities of these fluids as a function of simulation time at 50 and 80 ${}^{\circ }$C with their standard deviations are shown in Figure 3. The steady-state viscosity of the fluids at 50 and 80 ${}^{\circ }$C was calculated from the average of the running integral of the Green–Kubo formula over 40 and 20 NVE trajectories, respectively. The viscosities from the simulations are compared to measurements from the Cannon StressTech HR Oscillatory Rheometer in

Table 3. Comparison of simulated Newtonian viscosity of the three fluids with experimentally Newtonian viscosities. The error associated with all experimental data is ±0.2 mPa·s.

Temperature	Fluid ID	Viscosity (mPa·s)
		Experiment	Simulation
50 ${}^{\circ }$C	Fluid 1	40.2	39.7 ± 4.0
	Fluid 2	62.3	58.9 ± 3.2
	Fluid 3	35.45	38.6 ± 3.4
80 ${}^{\circ }$C	Fluid 1	15.9	15.7 ± 1.1
	Fluid 2	22.3	23.1 ± 1.0
	Fluid 3	13.5	14.3 ± 1.0

. This comparison shows that the simulation and measured viscosities are the same within the simulation and experimental error for both fluids at both temperatures. This indicates that the model systems are good representations of the formulated fluids.

Next we characterized the high-shear viscosity for the fluids using the PCS Ultra Shear viscometer at shear rates from $3\times {10}^5$ to $4\times {10}^6$ 1/s and NEMD simulations from $1\times {10}^8$ to $1\times {10}^{11}$ 1/s. These data were then combined with the Newtonian viscosity from EMD simulations (approximated as $1\times {10}^0$ 1/s) and the Cannon rheometer at shear rates of $7\times {10}^0$ to $1\times {10}^3$ 1/s to generate a complete viscosity profile across a wide range of shear rates. The results are shown in Figure 4, where hollow and solid symbols represent data from experiment and simulation, respectively. At both 50 and 80 ${}^{\circ }$C, all three fluids exhibit constant Newtonian viscosity at low shear rates, and then shear thin at high shear rates, as expected. The viscosity as a function of shear rate data $\eta \left(\dot{\gamma }\right)$ was then fit to the Carreau equation for shear thinning [62]:

$$\eta \left(\dot{\gamma }\right)={\eta }_{\infty }+({\eta }_0-{\eta }_{\infty }){[1+{\left(\lambda \dot{\gamma }\right)}^2]}^{\frac{n-1}{2}}$$

(2)

where ${\eta }_{\infty }$ is the viscosity at infinite shear rate and n is the power-law exponent. All viscosity data from simulations and experiments was fit to Equation (2) as shown by the dashed lines in Figure 4. The critical shear rates, the inverse of the fitted relaxation times, are reported in

Table 4. Critical shear rate of the fluids obtained from the Carreau fit to experiment and simulation viscosity data as compared to the theoretical prediction.

Temperature	Fluid ID	Critical Shear Rate (1/s)
		Experimental/Simulation	Prediction
50 ${}^{\circ }$C	Fluid 1	$5.27\times {10}^6$	$1.19\times {10}^6$
	Fluid 2	$2.78\times {10}^5$	$9.24\times {10}^5$
	Fluid 3	$2.71\times {10}^7$	$1.69\times {10}^7$
80 ${}^{\circ }$C	Fluid 1	$2.41\times {10}^6$	$3.38\times {10}^6$
	Fluid 2	$1.29\times {10}^6$	$2.91\times {10}^6$
	Fluid 3	$1.01\times {10}^8$	$4.54\times {10}^7$

. The complete set of fit parameters for Equation (2) is in Table S5.

The onset of shear thinning for Fluids 1 and 2 occurs in the key shear rate range for hydraulic pumps, indicated by the shaded regions in Figure 4. These two fluids were formulated with the same molecular weight PIB but different polymer concentrations and have approximately the same critical shear rate at 80 ${}^{\circ }$C. However, Fluid 2 has a lower critical shear rate at 50 ${}^{\circ }$C. In addition, Fluid 2 has significantly higher Newtonian viscosity both at 50 and 80 ${}^{\circ }$C than Fluid 1 due the larger concentration of polymer. We also observe that the critical shear rate of the fluids at 50 ${}^{\circ }$C is lower than that at 80 ${}^{\circ }$C. This is due to dependence of relaxation time and viscosity on temperature (Equation (1)). These results confirm that molecular weight governs critical shear rate, whereas concentration governs the Newtonian viscosity and the rate of shear thinning. This behavior is consistent with the predictions from the theoretical analysis.

The critical shear rates from the Carreau fit to experiment and/or simulation data for fluids are compared to the predictions from Equation (1) in Table 4. This comparison shows good agreement between prediction and observation. The minor differences are attributable to the assumption made in deriving Equation (1) that a single molecular weight contributes to the shear response of the fluid, which neglects the contribution of base oil molecules. The model also does not account for the architecture of molecules that contributes to the shear response. However, the results indicate that we were successful in using a simple model to identify a fluid formulation that shear thins in a specific range of shear rates, specifically the range of shear rates relevant to hydraulic machines.

To understand the observed shear thinning behavior, the simulations were used to analyze the change in molecular conformation due to shear stress. Temporary viscosity loss is expected to be caused by elongation of molecules in the direction of shear such that the molecules can provide less shear resistance, i.e., lower viscosity. To quantify this, we calculated the change in polymer length in the direction of shear from the NEMD simulations at each shear rate, averaged over time for all polymers in the simulation. The results are plotted vs. normalized viscosity (shear viscosity divided by Newtonian viscosity from EMD simulations) in Figure 5. Consistent with the expected mechanism of temporary viscosity loss, greater change in molecule length corresponds to lower viscosity.

Comparing the different fluids in Figure 5, at both temperatures, the average change in polymer length is much larger for Fluids 1 and 2 than for Fluid 3. This can be explained by the fact that Fluids 1 and 2 contain higher molecular weight polymers. These longer polymers require more time to respond to a given shear stress, i.e., they have longer relaxation times, and therefore have a lower critical shear rate (Table 4). The polymer length results also show that elongation depends on temperature. Particularly for Fluids 1 and 2, the change in polymer length is greater at 80 ${}^{\circ }$C than 50 ${}^{\circ }$C. This can be explained by the fact that there is more kinetic energy at a higher temperature, which enables the molecules to respond faster to shear. A faster response to shear corresponds to a shorter relaxation time and therefore a higher critical shear rate at 80 ${}^{\circ }$C.

4. Conclusions

Energy-efficient commercial hydraulic fluids are formulated with polymeric VMs that cause the fluids to exhibit shear thinning. While temporary viscosity loss is often viewed as detrimental, here it was explored as a potentially beneficial means of tuning the viscous behavior of a fluid. Particularly, we considered the possibility of using shear thinning to optimize the efficiency of hydraulic pumps for which efficiency is a non-monotonic function of viscosity. The ideal fluid for a hydraulic pump was identified as one with a critical shear rate between ${10}^4$ and ${10}^7$ 1/s and the Newtonian viscosity of 8–10 mPa·s at 80 ${}^{\circ }$C. A theoretical model was developed to predict critical shear rate and Newtonian viscosity as a function of the properties of the VM polymer and base oil, and their relative concentrations. The model was applied to PIB polymers of varying molecular weights in several different PAO base oils. This model predicted that a fluid formulated using 12 wt.% of 6 kg/mol PIB with PAO4 base oil should have a critical shear rate lower than ${10}^7$ 1/s with Newtonian viscosity of 8.9 mPa·s.

Based on the theoretical predictions, three fluids were formulated to validate the model and to distinguish the effects of molecular weight and concentration of polymer on the critical shear rate of the fluids. Fluids 1 and Fluid 2 were formulated using PAO4 base oil and 12 wt.% and 16 wt.% of 6.0 kg/mol PIB, respectively, and Fluid 3 was formulated using PAO8 base oil and 12 wt.% 1.3 kg/mol PIB. The viscosities of all three fluids across a wide range of shear rates were obtained using experimental measurements and atomistic simulations at 50 and 80 ${}^{\circ }$C. The low shear viscosities calculated from the simulations were consistent with those measured experimentally. The results indicate that the molecular weight of the polymer plays a key role in determining the critical shear rate, whereas the concentration of the polymer dominates the Newtonian viscosity. It was also found that the critical shear rates predicted by the theoretical model were consistent with the calculated critical shear rate using measured and simulated viscosities of fluids. This indicates that this model can be used more generally to predict critical shear rates of fluids and also formulate fluids that exhibit desired shear thinning profiles.

Finally, the shear thinning behavior of fluids was studied using the MD simulations. The simulations showed a direct correlation between the average change in polymer molecule length in the direction of shear to the normalized viscosity of fluids. The findings also confirmed that fluids formulated using longer polymers had lower critical shear rates because of their longer relaxation time, i.e., they take longer to respond to shear. Further, the simulations explained that critical shear rate is larger at higher temperatures because the additional kinetic energy enables fluids to respond to elongate in response to shear more quickly.

Overall, the results of this study and findings from our previous dynamometer study [25] suggest that Fluid 1 might increase mechanical efficiency without compromising the volumetric efficiency of the hydraulic pumps, since it is adequately susceptible to shear thinning in the key shear rate range of a pump and has an acceptable Newtonian viscosity for hydraulic machines. This is not the case for Fluid 2 because of its high Newtonian viscosity, nor for Fluid 3 that shear thins at a shear rate above that expected to occur in the pump. To validate this prediction, pump performance testing can be conducted in a dynamometer for these three fluids. In addition, the temperature dependency of the critical shear rate suggests that the fluid should be formulated to shear at a specific temperature range. More generally, this investigation provides a simple model for predicting critical shear rate that can be used to formulate polymer-enhanced hydraulic fluids that exhibit a shear thinning profile with a desired critical shear rate.