Temperature Dependent Solid Solution Strengthening in the High Entropy Alloy CrMnFeCoNi in Single Crystalline State

Abstract

The main difference between high entropy alloys and conventional alloys is the solid solution strengthening effect, which shifts from a single element to a multi-element matrix. Little is known about the effectiveness of this effect at high temperatures. Face-centered cubic, equiatomic, and single crystalline high entropy alloy CrMnFeCoNi was pre-alloyed by arc-melting and cast as a single crystal using the Bridgman process. Mechanical characterization by creep testing were performed at temperatures of 700, 980, 1100, and 1200 °C at different loads under vacuum and compared to single-crystalline pure nickel. The results allow a direct assessment of the influence of the chemical composition without any disturbance by grain boundary sliding or diffusion. The results indicate different behaviors of single crystalline pure nickel and CrMnFeCoNi. At 700 °C CrMnFeCoNi is more creep-resistant than Ni, but at 980 °C both alloys show a nearly similar creep strength. Above 980 °C the creep behavior is identical and the solid solution strengthening effect of the CrMnFeCoNi alloy disappears.

1. Introduction

During the last 15 years, research in the field of high entropy alloys (HEA) and compositionally complex alloys (CCA) has shown enormous growth [1,2,3,4]. Per definition, a HEA is a solid solution crystal consisting of at least five alloying elements in near equiatomic ratio [5] and, therefore, there is no base element dominating the composition. Only a few HEA stand out by not having a multiphase microstructure, but rather a simple disordered solid solution microstructure, which maximizes the configurational entropy ΔS_conf [6]. The latter is directly linked to the solid solution strengthening behavior in HEA and CCA [7,8]. Such alloys have higher strength than pure elements due to the solute atoms dissolved in the solvent matrix which provide resistance to dislocation motion. Solid solution strengthening (often referred in context with lattice distortion and subsequently sluggish diffusion) is a way to increase the strength of a metal by alloying elements [9,10,11,12,13].

A very common high entropy alloy is CrMnFeCoNi, often called Cantor alloy. Previous studies using this alloy focused on polycrystalline structure and on higher temperatures [14,15,16,17,18,19,20]. The influence of grains or varying grain size on the mechanical properties of the CrMnFeCoNi alloy was investigated by Sun et al. [20]. With regard to the formation of phase separation and precipitation as a function of temperature, important impact factors have been studied by Joseph and Otto et al. [21,22]. Their work shows that, at intermediate temperatures above 800 °C, CrMnFeCoNi shows a single-phase structure after an ageing period of 500 days, but at 700 °C and below precipitates form exclusively at the grain boundaries and pores [22]. This shows that the choice of temperature is an important factor to consider for long-term mechanical characterization like creep experiments. In addition the diffusion behavior (often referred in relation to sluggish diffusion) of the individual elements in the alloy, for example by bulk and grain boundary diffusion, must also be considered [23,24].

The previous works on CrMnFeCoNi with polycrystalline structure are very application-oriented and tunable by several processes such as grain refinement, cold working, recrystallization or combinations of these. To the moment, there is little knowledge of a state close to the equilibrium, which serves as a base on which all other states can be referred to. This state close to equilibrium can be approximated using an unconstrained single crystal (SX), where no influence of grains or deformation effect the inherent material properties. Therefore, single crystalline CrMnFeCoNi samples allow the investigation of the pure material properties without effects linked to grain boundaries like grain size, grain boundary diffusion or formation of precipitates. So far, mechanical properties on Cantor single crystals have only been carried out in the temperature range of −196 °C to 300 °C, both in tension and compression [25,26,27]. The behavior at temperatures higher than 300 °C is unknown, yet important to thoroughly understand the material.

To investigate the time-dependent mechanical properties at higher temperatures, creep testing is a suitable method. Creep deformation is a diffusion-controlled mechanism that is activated at temperatures above 40% of the materials melting temperature T_m. The predominant deformation mechanism is non-conservative dislocation movement by climbing even at very low stress levels. In addition, the effect of solid solution strengthening (in the context with sluggish diffusion kinetics) of two alloys can also be investigated by creep testing, as Fleischmann et al. showed [28] by comparing two Ni-based superalloys by adding Re to one of the two alloys.

The aim of this work is to fill the high temperature knowledge gap by studying the creep properties of a single crystal. This does provide an understanding of the solid solution strengthening and dislocation movement, excluding diffusion and effects at grain boundaries. This will be achieved by comparing two face centered cubic (fcc) single phase single crystals with different configurational entropy: the solid solution CrMnFeCoNi with ΔS_conf = 1.61 × R (R = universal gas constant 8.314 J mol⁻¹ K⁻¹) and pure Ni with ΔS_conf = 0 × R, which exhibits no solid solution [29].

2. Materials and Methods

2.1. Alloy Fabrication

Elements with a technical purity of at least 99.99% were used for the production of the CrMnFeCoNi alloy. In a first step, the elements were melted in an arc-melting furnace (Edmund Bühler GmbH, Bodelshausen, Germany) under argon to form master alloys with a diameter of 35–40 mm and a height of 7–9 mm. In order to achieve sufficient chemical homogeneity, the ingots were flipped at least six times. All ingots were analyzed by micro X-ray fluorescence (µ-XRF, AMETEK, Berwyn PA, USA), which shows a homogeneous element distribution of 20 ± 1.0 at% per element. In the second step, a total mass of 400 g (eight master alloys ingots) is placed in a zirconium oxide crucible and put in the center of a water-cooled copper coil of an induction casting device (Metals and Alloys, University of Bayreuth, Bayreuth, Germany) [30,31]. The ceramic mold with a helical grain selector was heated up to 1450 °C (100 °C above the solidus temperature [29]) in a second induction coil. Subsequently, the master alloy is heated in the crucible to approximately 1600 °C by induction, homogenized in liquid state for 5 min and cast into the pre-heated ceramic mold. The ceramic mold was pulled through a water-cooled baffle with a speed of 3 mm/min resulting in a total solidification time of 1–2 h. The single crystal solidifies in [001] orientation with a maximum deviation of 3°. To prevent manganese loss due to evaporation argon (5 × 10⁴ Pa) was used as atmosphere. Thereby manganese loss does not occur during the single crystal casting process (see Figure 1). In addition, single crystalline pure nickel was cast as in the same way but under vacuum.

All single crystalline samples were cast in a cylindrical shape with about 16 mm in diameter and a length of 170 mm. The samples were sandblasted and etched with a solution of 100 mL H₂O, 200 mL HCl, 60 g FeCl₃·6 H₂O and 12 g (NH₄) 2 [CuCl₄]·2 H₂O (Adler etch) to remove adhering mold shell residues. The quality check of both single crystals by electron backscatter diffraction (EBSD, AMETEK, Berwyn PA, USA) shows no further grains and a crystallographic orientation of [001] ± 3° for CrMnFeCoNi and 8° for pure Ni.

To verify the equiatomic composition of the cast CrMnFeCoNi alloy, the sample was ground along the sample length with SiC paper 320 to obtain a plane surface for µ-XRF measurement (linescan). Figure 1 shows a constant equiatomic distribution with 20 ± 1.0 at% for each element of the sample cast in argon atmosphere. The measurement was carried out on the SX main body of the sample. In comparison, the use of vacuum as process atmosphere leads to an inhomogeneous element distribution, because of the evaporation of manganese [23,24].

2.2. Sample Preparation

Creep samples for mechanical testing were prepared by wire electronic discharge machining (EDM). All creep samples were etched with V2 etch, a solution of 100 mL HCl, 100 mL H₂O, 10 mL HNO₃ and 1 mL pickling solution, to remove the remaining layer of wire EDM and with the side effect of bringing out the dendritic structure. Before testing, the samples were ground with SiC paper 2400. The samples had a rectangular cross-section of 1.0 × 2.9 mm, a measuring length of 5 mm, and a total length of 30 mm and were similar to the geometry reported in [32].

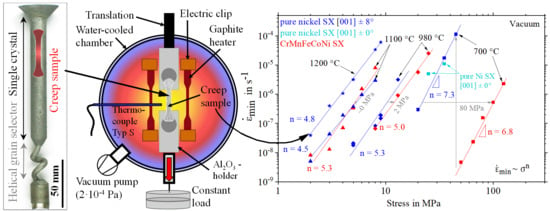
2.3. Mechanical Testing

Creep tests were carried out under vacuum (2 × 10⁻⁴ Pa) using a vacuum creep testing device (Metals and Alloys, University of Bayreuth, Bayreuth, Germany) as described in [33]. The tests were performed at high temperatures of 700, 980, 1100, and 1200 °C, controlled by a type-S thermocouple close to the sample. The specimens were griped by Al₂O₃ rods and heated up to the test temperature with a rate of 20 K/min in a resistance-heated furnace. The strain was measured by non-contacting video extensometer [34]. The load was chosen in the range of 2–125 MPa in order to achieve stationary creep rates in a wide range of 10⁻⁸–10⁻³ s⁻¹. As a starting point for determination of the creep loads, the yield strength of tensile tests according to [35] were determined with an strain rate of 10⁻³ s⁻¹ at 700 and 1000 °C using the same sample geometry. This test resulted in a yield strength of 46 MPa at 700 °C and 7 MPa at 1000 °C for pure nickel and 62 MPa at 700 °C and 42 MPa at 1000 °C for CrMnFeCoNi.

3. Results and Discussion

The applied creep loads were selected below the yield strengths from tensile tests at 700 and 1000 °C. For all investigated creep samples, the strains in the primary and secondary creep range were uniform along the specimen length. In the tertiary area up to the failure, there is only deformation along the gauge length between the ridges. The following results show the deformation as an engineering strain.

The creep results for CrMnFeCoNi (red) and pure nickel (blue) are plotted as creep rate over strain at 700 °C in Figure 2 and Figure 3 and at 980 °C in Figure 4. At 700 °C testing temperature, the tests at 50 and 65 MPa for CrMnFeCoNi (Figure 2a) and at 20 MPa for pure nickel (Figure 2b) were interrupted for further investigations (marked with open circles). At 980 °C the test at 8 MPa for CrMnFeCoNi (Figure 4a) and 5, 8, and 9 MPa for pure nickel (Figure 4b) were interrupted. All other tests were carried out until fracture (marked with black crosses in Figure 2 and Figure 4). The strain to failure was in almost all cases higher than 30%. At both temperatures, the minimum creep rate of pure nickel is achieved at higher strain levels, i.e., much higher than 2%. The minimum creep rate of the CrMnFeCoNi alloy is always reached at less than 2% strain at both temperatures. This effect may be based on the different deviations of the two singe crystals from the [001] orientation. The deviation from the [001] orientation of the pure nickel samples was 8° and therefore 5° higher than that of the CrMnFeCoNi samples. Primary creep is known to be sensitive to orientation [36,37,38,39]: Deviations from the [001] axis, which are close to the [001]–[111] diagonal, resulting in an increased primary creep regime.

Perfectly oriented SX-Ni creep samples with a deviation of the orientation of [001] ± 0° were prepared and tested at a temperature of 700 °C to investigate the influence of the orientation deviation on the minimum creep rate. Figure 2b shows the results of these creep tests as light blue creep curves for 25 and 35 MPa loads. In both cases the tests show a normal, not pronounced primary creep behavior. The minimum creep rate of both tests is reached earlier than for the Ni samples with 8° deviation. Figure 3 shows the comparison of the creep results for 0° and 8° deviation samples at a load of 35 MPa in more detail. For 8° deviation the minimum creep rate of 1.8 × 10⁻⁵ 1/s is achieved at 26% strain, whereas for 0° deviation it is already achieved after 11% at a similar creep rate of 1.0 × 10⁻⁵ 1/s (Figure 3a). This shows that primary creep behavior (Figure 3b) is sensitive to orientation, but without any influence on the minimum creep rate.

Figure 5 and Figure 6 show the creep results for pure nickel and CrMnFeCoNi at 1100 °C and 1200 °C, respectively. All tests were started with a stress level of 2 MPa. Afterwards, the stress was increased stepwise up to 8 MPa at 1100 °C and 10 MPa at 1200 °C, whenever it was obvious that the minimum creep rate was reached. The stepwise stress increase at the temperature of 1100 °C was identical for both materials (Figure 5a,b). For each increase, the reduction of the specimen cross-section A_0-new was calculated (equation in Figure 5). A₀ is the initial cross section of the specimen, A_0-new is the difference between A₀ and A_new and ε_{load before} is the achieved strain until load increase. Thus, the strain up to the load increase was considered.

Both tests at 1100 °C were interrupted, the one in pure nickel after 358 h and the one in CrMnFeCoNi after 280 h. At 1200 °C (Figure 6), two pure Ni specimens were tested with a stepwise load increase until fracture. The testing times were 3.5 h and 45 h. Due to high evaporation rates of manganese, no creep tests could be carried out for CrMnFeCoNi at this high temperature.

Based on the creep results plotted in Figure 2, Figure 3, Figure 4, Figure 5 and Figure 6 the minimum creep rate ${\dot{\mathsf{\epsilon }}}_{\min }$ is determined using Equation (1) and listed in

Table 1. Minimum creep rates and stress exponents for the creep tests of pure nickel and CrMnFeCoNi at different loads and temperatures under vacuum.

	${\mathbf{log}}_{10}{\dot{\mathcal{E}}}_{\mathbf{min}}\mathbf{in} \mathbf{s}{-}^1$
Material	SX-Ni				SX-CrMnFeCoNi
Temperature in °C	700	980	1100	1200	700	980	1100
Load in MPa
2			−8.2	−7.4			−8.1
3			−7.5	−6.4			−7.9
4			−6.7	−6.0			−7.1
5		−7.7	−6.4	−5.5			−6.5
6			−6.0				−5.8
8		−7.1	−5.5	−4.5		−7.2	−5.1
9		−6.8		−4.2
13		−5.5				−6.0
20	−6.5					−5.2
25	−5.3 1					−4.6
35	−4.8/–5.0 1
45	−4.0
50					−8.3
65					−7.6
80					−6.8
100					−6.3
125					−5.6
Norton exp. n	7.3	5.3	4.5	4.8	6.8	5.0	5.3

¹ Creep samples with deviation from [001] ± 0°.

(where n is called Norton exponent or stress exponent). Using a double-logarithmic scaling, the minimum creep rate ${\dot{\mathsf{\epsilon }}}_{\min }$ is plotted over the applied stress σ (Norton plot, Figure 7). Both pure nickel and CrMnFeCoNi show a linear relationship between these two parameters.

$${\dot{\mathsf{\epsilon }}}_{\min }={ \mathsf{\sigma }}^{\mathrm{n}}$$

(1)

It is known that for a stress exponent n ≈ 1, volume or grain boundary diffusion are dominating, and for n = 3–5 the single-phase material deforms by dislocation climb [40,41]. The Norton exponents of pure nickel and CrMnFeCoNi at 980 °C are almost identical, i.e., n = 5.3 for nickel and 5.0 for the Cantor alloy. At 1100 °C the stress exponents are also close to each other, i.e., n = 4.5 for pure nickel and 5.3 for the CrMnFeCoNi alloy. Furthermore, for both temperatures, there is nearly no difference in the stress level (horizontal displacement) between the two materials at the same creep rate. At 1100 °C the difference is 0 MPa and at 980 °C only 2 MPa. Thus, there is only a very small effect of solid solution strengthening in the CrMnFeCoNi alloy in comparison to pure Ni at 980 °C and no solid solution strengthening at 1100 °C.

At a temperature of 700 °C a considerable difference in the horizontal displacement of the creep resistance can be detected between pure nickel and CrMnFeCoNi, despite n being very close (7.3 for pure Ni and 6.8 for the CrMnFeCoNi alloy). The minimum creep rates of the tested Ni samples (light blue dots) at 700 °C with a deviation from [001] ± 0°, are in the same range as the results of Ni with 8° deviation. For pure Ni a measurement at 50 MPa was not possible, because 45 MPa is already in the range of the yield strength and conventional dislocation glide takes place. Therefore, the creep rate of 1 × 10⁻⁴ 1/s is already in the range as tensile tests and the time to failure was less than 0.1 h. The plotted line of pure Ni was extrapolated to a value of 50 MPa to compare it with CrMnFeCoNi. The minimum creep rate of pure nickel is more than three orders of magnitude higher than that of CrMnFeCoNi at 50 MPa: The necessary stress for achieving a minimum creep rate ${\dot{\mathsf{\epsilon }}}_{\min }$ of 1 × 10⁻⁶ s⁻¹ is 80 MPa higher for CrMnFeCoNi than for pure Ni.

At the lower temperature of 700 °C solid solution strengthening (in the context to sluggish diffusion) based on a high configurational entropy is, therefore, particularly more effective than at 980 and 1100 °C.

The Larson–Miller plot (Figure 8a) compares the time necessary for reaching 2% strain (t_2% in h) for the different temperatures 700, 980, 1100 and 1200 °C and stress levels. The time to reach 2% strain is more relevant in the field of application and better reproducible than the time to failure. Equation (2) is used to calculate the Larson-Miller parameter P_2%, where T is the temperature in K:

$${\mathrm{P}}_{2\%}= \frac{\mathrm{T}}{1 \mathrm{K}}\times \left(20+\log \frac{{\mathrm{t}}_{2\%}}{1 \mathrm{h}}\right) \times {10}^{-3}$$

(2)

The values determined for t_2% are listed in

Table 2. Time to reach 2% strain for the creep tests in pure nickel and CrMnFeCoNi at different loads and temperatures under vacuum.

	t2% in h
Material	SX-Ni				SX-CrMnFeCoNi
Temperature in °C	700	980	1100	1200	700	980	1100
Load in MPa
2			740.7	28.4 2			564.4 2
3			70.8	6.7			289.5 2
4			9.5	1.5			72.0 2
5		32.0					15.2
8		1.5				72.0
9		0.7
13		0.1				5.0
20	3.1					1.0
25	0.8 1					0.2
35	0.1/0.2 1
45	<0.1
50					830.0 2
65					130.0
80					35.0
100					3.5
125					0.3

¹ Creep samples with deviation from [001] ± 0°. ² Extrapolated after reaching the minimum creep rate.

. For the tests using stress increase only the values up to a total strain of 5% were determined. At low loads of 2 MPa, the load increases were carried out before the 2% limit was reached, because the minimum creep rate was achieved. Therefore, the time to reach 2% were extrapolated. Both pure nickel and CrMnFeCoNi show a linear behavior at different slopes. For pure nickel the slope is −0.09 and for CrMnFeCoNi it is −0.15. The results of the Ni samples with the deviation from [001] ± 0° lie in the same range as the results of the samples with 8° deviation. The straight lines diverge at lower temperature (or increasing stress level). This is due to the increasing solid solution strengthening effect with decreasing temperature. At higher temperatures above 980 °C and a low load of 2 MPa the point of intersection of both materials can be identified. The value for the Larson–Miller parameter P_2% at this point is 31.7.

The use of the absolute temperature for the Larson–Miller plot is particularly suitable in case for possible applications. However, for a pure scientific consideration the use of the homologous temperature of both materials is more suitable. The homologous temperatures T_H can be determined by ${\mathrm{T}}_{\mathrm{H} }= \frac{\mathrm{T}}{{\mathrm{T}}_{\mathrm{m}}}$ using the melting points T_m for both materials, with 1607 K for CrMnFeCoNi and 1728 K for pure Ni. By changing T to T/T_m in Equation (2), the Larson–Miller parameter for homologous temperature can be calculated.

The Larson–Miller plot as a function of T_H is shown in Figure 8b. As already shown in Figure 8a, there exists also a difference in the slope of materials, –0.16 for pure nickel and −0.24 for CrMnFeCoNi. The characteristic feature between Figure 8a,b is a shift to the left of pure Ni, which increases the difference between the two materials from 80 MPa (Figure 8a) to 105 MPa (Figure 8b).

Assuming a constant load and the same time for t_2% of 10 h, the temperature difference between the two materials can be determined from Figure 8b. At 50 MPa, the CrMnFeCoNi alloy requires 198 K more than pure Ni to achieve a strain of 2% in the same time. This difference decreases to higher temperatures, therefore, at 3 MPa there is only a difference of 37 K.

The statement is finally identical to the conclusion from the plot using the absolute temperature: at lower temperatures the solid solution strengthening increases.

In order to get an overview of the dislocation structure of both materials, selected interrupted creep samples will be examined using electron channeling contrast imaging (ECCI). The results of this microstructural analysis will be correlated with the mechanical properties. This will be used to determine if there are any fundamental differences in dislocation movement between the Cantor alloy and pure nickel. In case of the low stresses and the resulting stress exponents of 4 ≤ n ≤ 7, a stress assisted dislocation climb controlled by lattice diffusion can be expected for CrMnFeCoNi [42].

4. Conclusions

In summary, the following conclusions can be drawn for the mechanical characterization of CrMnFeCoNi alloy and pure nickel as single crystals:

• Creep testing of single crystals under vacuum allows a comparison of pure solid solution strengthening, excluding oxidation effects, grain size effects, grain boundary sliding, diffusion, and no precipitate effects.
• The 8° deviation from the [001] orientation for SX-Ni leads to an orientation sensitive primary creep behavior compared to [001] ± 0°, but there is no detected effect on the minimum creep rate.
• The SX CrMnFeCoNi alloy has a strong solid solution strengthening effect at 700 °C compared to SX pure nickel. The stress necessary to reach the same creep rate is 80 MPa higher in CrMnFeCoNi than in Ni.
• The solid solution strengthening effect due to high configurational entropy depends on the temperature and is strongly reduced at 980 °C and no longer present at 1100 °C.