Revealing the Dynamic Transformation of Austenite to Bainite during Uniaxial Warm Compression through In-Situ Synchrotron X-ray Diffraction
Abstract
:1. Introduction
2. Materials and Methods
3. Results and Discussion
3.1. Kinetics of Dynamic Transformation
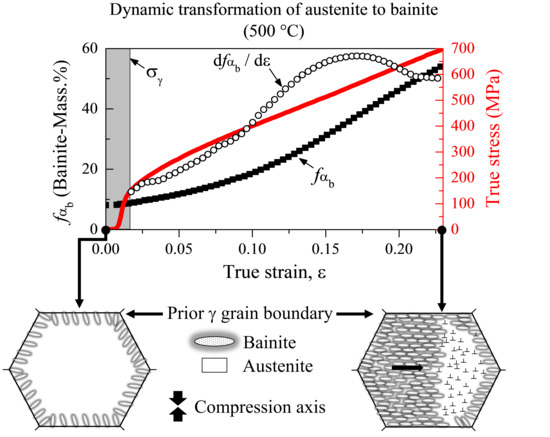
3.1.1. Phase Content during Deformation
3.1.2. Peak Broadening
3.1.3. Lattice Parameter
3.2. Lattice Strains during Dynamic Transformation
3.3. Kinetics of Phase Transformation during DT and Isothermal Transformation
3.4. Ex-Situ Microstructure
4. Conclusions
- The kinetics of bainite is accelerated through DT(γ→αb) at 500 °C in comparison with pure isothermal treatment;
- Plastic deformation triggers the DT(γ→αb), which is continuously stimulated because lattice defects are introduced preferentially in the austenite;
- Based on real-time evidence, it was proposed that the DT(γ→αb) is ruled by the dynamic introduction of dislocations, which enable the progress of the transformation without mechanical stabilization of austenite;
- The partitioning of alloying elements during DT is suggested to occur under paraequilibrium conditions (i.e., only carbon partitioning);
- The bainitic microstructure in the sample subjected to DT(γ→αb) is preferentially orientated perpendicular to the compression direction. Furthermore, both microstructural refinement and hardness increase were obtained in comparison with the reference microstructure; and
- It is important to emphasize that even though the strain rate employed in the present investigation does not necessarily reflect typical values applied in the industrial warm forgings and/or controlled rolling processes, the DT(γ→αb) may represent a potential strategy aiming at energy-efficient manufacturing processes, since phase transformation and plastic deformation are taking place simultaneously. Besides, DT(γ→αb) sheds new insights into design carbide-free bainitic microstructures via thermomechanical processing.
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lemos Bevilaqua, W.; Epp, J.; Meyer, H.; Da Silva Rocha, A.; Roelofs, H. In Situ Investigation of the Bainitic Transformation from Deformed Austenite During Continuous Cooling in a Low Carbon Mn-Si-Cr-Mo Steel. Metall. Mater. Trans. A 2020, 51, 3627–3637. [Google Scholar] [CrossRef]
- Silveira, A.C.d.F.; Bevilaqua, W.L.; Dias, V.W.; de Castro, P.J.; Epp, J.; Rocha, A.d.S. Influence of Hot Forging Parameters on a Low Carbon Continuous Cooling Bainitic Steel Microstructure. Metals 2020, 10, 601. [Google Scholar] [CrossRef]
- Kaikkonen, P.M.; Somani, M.C.; Miettunen, I.H.; Porter, D.A.; Pallaspuro, S.T.; Kömi, J.I. Constitutive flow behaviour of austenite at low temperatures and its influence on bainite transformation characteristics of ausformed medium-carbon steel. Mater. Sci. Eng. A 2020, 775, 12. [Google Scholar] [CrossRef]
- Eres-Castellanos, A.; Caballero, F.G.; Garcia-Mateo, C. Stress or strain induced martensitic and bainitic transformations during ausforming processes. Acta Mater. 2020, 189, 60–72. [Google Scholar] [CrossRef]
- He, J.; Du, J.; Zhang, W.; Zhang, C.; Yang, Z.-G.; Chen, H. Abnormal Anisotropic Dilatation During Bainitic Transformation of Ausformed Austenite. Metall. Mater. Trans. A 2019, 50, 540–546. [Google Scholar] [CrossRef]
- van Bohemen, S.M.C. Bainite growth retardation due to mechanical stabilisation of austenite. Materialias 2019, 7, 17. [Google Scholar] [CrossRef]
- Zhao, L.; Qian, L.; Zhou, Q.; Li, D.; Wang, T.; Jia, Z.; Zhang, F.; Meng, J. The combining effects of ausforming and below-Ms or above-Ms austempering on the transformation kinetics, microstructure and mechanical properties of low-carbon bainitic steel. Mater. Des. 2019, 183, 108–123. [Google Scholar] [CrossRef]
- Eres-Castellanos, A.; Hidalgo, J.; Zorgani, M.; Jahazi, M.; Toda-Caraballo, I.; Caballero, F.G.; Garcia-Mateo, C. Assessing the scale contributing factors of three carbide-free bainitic steels: A complementary theoretical and experimental approach. Mater. Des. 2021, 197, 15. [Google Scholar] [CrossRef]
- Eres-Castellanos, A.; Morales-Rivas, L.; Latz, A.; Caballero, F.G.; Garcia-Mateo, C. Effect of ausforming on the anisotropy of low temperature bainitic transformation. Mater. Charact. 2018, 145, 371–380. [Google Scholar] [CrossRef]
- Guo, L.; Bhadeshia, H.K.D.H.; Roelofs, H.; Lembke, M.I. In situ synchrotron X-ray study of bainite transformation kinetics in a low-carbon Si-containing steel. Mater. Sci. Technol. 2017, 33, 2147–2156. [Google Scholar] [CrossRef]
- Onuki, Y.; Hirano, T.; Hoshikawa, A.; Sato, S.; Tomida, T. In Situ Observation of Bainite Transformation and Simultaneous Carbon Enrichment in Austenite in Low-Alloyed TRIP Steel Using Time-of-Flight Neutron Diffraction Techniques. Metall. Mater. Trans. A 2019, 50, 4977–4986. [Google Scholar] [CrossRef] [Green Version]
- Rementeria, R.; Jimenez, J.A.; Allain, S.Y.P.; Geandier, G.; Poplawsky, J.D.; Guo, W.; Urones-Garrote, E.; Garcia-Mateo, C.; Caballero, F.G. Quantitative assessment of carbon allocation anomalies in low temperature bainite. Acta Mater. 2017, 133, 333–345. [Google Scholar] [CrossRef]
- Babu, S.S.; Specht, E.D.; David, S.A.; Karapetrova, E.; Zschack, P.; Peet, M.; Bhadeshia, H.K.D.H. In-situ observations of lattice parameter fluctuations in austenite and transformation to bainite. Metall. Mater. Trans. A 2005, 36, 3281–3289. [Google Scholar] [CrossRef]
- Gong, W.; Tomota, Y.; Adachi, Y.; Paradowska, A.M.; Kelleher, J.F.; Zhang, S.Y. Effects of ausforming temperature on bainite transformation, microstructure and variant selection in nanobainite steel. Acta Mater. 2013, 61, 4142–4154. [Google Scholar] [CrossRef]
- Reisinger, S.; Kozeschnik, E.; Ressel, G.; Keckes, J.; Stark, A.; Marsoner, S.; Ebner, R. Strain energy contributions on the bainitic phase transformation in a CrMoV steel during continuous cooling. Mater. Des. 2018, 155, 475–484. [Google Scholar] [CrossRef]
- Shi, Z.; Tomota, Y.; Harjo, S.; Su, Y.; Chi, B.; Pu, J.; Jian, L. Effect of non-isothermal deformation of austenite on ferrite transformation behavior studied by in-situ neutron diffraction. Mater. Sci. Eng. A 2015, 631, 153–159. [Google Scholar] [CrossRef]
- Dutta, R.K.; Huizenga, R.M.; Amirthalingam, M.; Gao, H.; King, A.; Hermans, M.J.M.; Richardson, I.M. In-situ synchrotron diffraction studies on hot deformation of austenite in a high strength quenched and tempered structural steel. Adv. Mater. Res. 2014, 922, 126–131. [Google Scholar] [CrossRef]
- Epp, J.; Dong, J.; Meyer, H.; Bohlen, A. Analysis of cyclic phase transformations during additive manufacturing of hardenable tool steel by in-situ X-ray diffraction experiments. Scr. Mater. 2020, 177, 27–31. [Google Scholar] [CrossRef]
- Barriobero-Vila, P.; Gussone, J.; Kelm, K.; Haubrich, J.; Stark, A.; Schell, N.; Requena, G. An in situ investigation of the deformation mechanisms in a β-quenched Ti-5Al-5V-5Mo-3Cr alloy. Mater. Sci. Eng. A 2018, 717, 134–143. [Google Scholar] [CrossRef]
- van Bohemen, S.M.C.C. Bainite and martensite start temperature calculated with exponential carbon dependence. Mater. Sci. Technol. 2011, 28, 487–495. [Google Scholar] [CrossRef]
- Ashiotis, G.; Deschildre, A.; Nawaz, Z.; Wright, J.P.; Karkoulis, D.; Picca, F.E.; Kieffer, J. The fast azimuthal integration Python library: PyFAI. J. Appl. Crystallogr. 2015, 48, 510–519. [Google Scholar] [CrossRef]
- He, S.H.; He, B.B.; Zhu, K.Y.; Huang, M.X. Evolution of dislocation density in bainitic steel: Modeling and experiments. Acta Mater. 2018, 149, 46–56. [Google Scholar] [CrossRef]
- Allain, S.Y.P.; Gaudez, S.; Geandier, G.; Danoix, F.; Soler, M.; Goune, M. Carbon heterogeneities in austenite during Quenching & Partitioning (Q&P) process revealed by in situ High Energy X-ray Diffraction (HEXRD) experiments. Scr. Mater. 2020, 181, 108–114. [Google Scholar] [CrossRef] [Green Version]
- van Bohemen, S.M.C. Exploring the correlation between the austenite yield strength and the bainite lath thickness. Mater. Sci. Eng. A 2018, 731, 119–123. [Google Scholar] [CrossRef]
- Kalidindi, S.R. Modeling the strain hardening response of low SFE FCC alloys. Int. J. Plast. 1998, 14, 1265–1277. [Google Scholar] [CrossRef]
- Ravi, A.M.; Navarro-López, A.; Sietsma, J.; Santofimia, M.J. Influence of martensite/austenite interfaces on bainite formation in low-alloy steels below Ms. Acta Mater. 2020, 188, 394–405. [Google Scholar] [CrossRef]
- Ravi, A.M.; Sietsma, J.; Santofimia, M.J. Exploring bainite formation kinetics distinguishing grain-boundary and autocatalytic nucleation in high and low-Si steels. Acta Mater. 2016, 105, 155–164. [Google Scholar] [CrossRef] [Green Version]
- Hu, H.; Zurob, H.S.; Xu, G.; Embury, D.; Purdy, G.R. New insights to the effects of ausforming on the bainitic transformation. Mater. Sci. Eng. A 2015, 626, 34–40. [Google Scholar] [CrossRef]
- Larn, R.H.; Yang, J.R. The effect of compressive deformation of austenite on the bainitic ferrite transformation in Fe-Mn-Si-C steels. Mater. Sci. Eng. A 2000, 278, 278–291. [Google Scholar] [CrossRef]
- Gong, W.; Tomota, Y.; Koo, M.S.; Adachi, Y. Effect of ausforming on nanobainite steel. Scr. Mater. 2010, 63, 819–822. [Google Scholar] [CrossRef]
- Bhadeshia, H.K.D.H.; Christian, J.W. Bainite in steels. Metall. Trans. A 1990, 21, 767–797. [Google Scholar] [CrossRef]
- Hidalgo, J.; Huizenga, R.M.; Findley, K.O.; Santofimia, M.J. Interplay between metastable phases controls strength and ductility in steels. Mater. Sci. Eng. A 2019, 745, 185–194. [Google Scholar] [CrossRef]
- Brandstetter, S.; Budrović, Ž.; Van Petegem, S.; Schmitt, B.; Stergar, E.; Derlet, P.M.; Van Swygenhoven, H. Temperature-dependent residual broadening of x-ray diffraction spectra in nanocrystalline plasticity. Appl. Phys. Lett. 2005, 87, 2. [Google Scholar] [CrossRef] [Green Version]
- Ebner, S.; Schnitzer, R.; Suppan, C.; Stark, A.; Liu, H.; Hofer, C. Characterization of carbides in Q&P steels using a combination of high-resolution methods. Mater. Charact. 2020, 163, 110242. [Google Scholar] [CrossRef]
- Blondé, R.; Jimenez-Melero, E.; Zhao, L.; Wright, J.P.; Brück, E.; van der Zwaag, S.; van Dijk, N.H. High-energy X-ray diffraction study on the temperature-dependent mechanical stability of retained austenite in low-alloyed TRIP steels. Acta Mater. 2012, 60, 565–577. [Google Scholar] [CrossRef]
- Dutta, R.K.; Huizenga, R.M.; Amirthalingam, M.; King, A.; Gao, H.; Hermans, M.J.M.; Richardson, I.M. In situ synchrotron diffraction studies on the temperature-dependent plane-specific elastic constants in a high-strength quenched and tempered structural steel. Scr. Mater. 2013, 69, 187–190. [Google Scholar] [CrossRef]
- Shibata, A.; Takeda, Y.; Park, N.; Zhao, L.; Harjo, S.; Kawasaki, T.; Gong, W.; Tsuji, N. Nature of dynamic ferrite transformation revealed by in-situ neutron diffraction analysis during thermomechanical processing. Scr. Mater. 2019, 165, 44–49. [Google Scholar] [CrossRef]
- Ravi, A.M.; Kumar, A.; Herbig, M.; Sietsma, J.; Santofimia, M.J. Impact of austenite grain boundaries and ferrite nucleation on bainite formation in steels. Acta Mater. 2020, 188, 424–434. [Google Scholar] [CrossRef]
- Ghosh, C.; Aranas, C.; Jonas, J.J. Dynamic transformation of deformed austenite at temperatures above the Ae3. Prog. Mater. Sci. 2016, 82, 151–233. [Google Scholar] [CrossRef] [Green Version]
- Park, N.; Zhao, L.; Shibata, A.; Tsuji, N. Dynamic Ferrite Transformation Behaviors in 6Ni-0.1C Steel. JOM 2014, 66, 765–773. [Google Scholar] [CrossRef]
- Adachi, Y.; Xu, P.G.; Tomota, Y. Crystallography and Kinetics of Dynamic Transformation in Steels. ISIJ Int. 2008, 48, 1056–1062. [Google Scholar] [CrossRef] [Green Version]
- Guo, B.; Liu, Y.; Jonas, J.J. Dynamic Transformation of Two-Phase Titanium Alloys in Stable and Unstable States. Metall. Mater. Trans. A 2019, 50, 4502–4505. [Google Scholar] [CrossRef]
- Hase, K.; Garcia-Mateo, C.; Bhadeshia, H.K.D.H. Bainite formation influenced by large stress. Mater. Sci. Technol. 2004, 20, 1499–1505. [Google Scholar] [CrossRef] [Green Version]
- Reisinger, S.; Ressel, G.; Eck, S.; Marsoner, S. Differentiation of grain orientation with corrosive and colour etching on a granular bainitic steel. Micron 2017, 99, 67–73. [Google Scholar] [CrossRef]
- Cornide, J.; Garcia-Mateo, C.; Capdevila, C.; Caballero, F.G. An assessment of the contributing factors to the nanoscale structural refinement of advanced bainitic steels. J. Alloys Compd. 2013, 577, S43–S47. [Google Scholar] [CrossRef]
- Singh, S.B.; Bhadeshia, H.K.D.H. Estimation of bainite plate-thickness in low-alloy steels. Mater. Sci. Eng. A 1998, 245, 72–79. [Google Scholar] [CrossRef]







Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2021 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bevilaqua, W.L.; Epp, J.; Meyer, H.; Dong, J.; Roelofs, H.; da Silva Rocha, A.; Reguly, A. Revealing the Dynamic Transformation of Austenite to Bainite during Uniaxial Warm Compression through In-Situ Synchrotron X-ray Diffraction. Metals 2021, 11, 467. https://doi.org/10.3390/met11030467
Bevilaqua WL, Epp J, Meyer H, Dong J, Roelofs H, da Silva Rocha A, Reguly A. Revealing the Dynamic Transformation of Austenite to Bainite during Uniaxial Warm Compression through In-Situ Synchrotron X-ray Diffraction. Metals. 2021; 11(3):467. https://doi.org/10.3390/met11030467
Chicago/Turabian StyleBevilaqua, William Lemos, Jérémy Epp, Heiner Meyer, Juan Dong, Hans Roelofs, Alexandre da Silva Rocha, and Afonso Reguly. 2021. "Revealing the Dynamic Transformation of Austenite to Bainite during Uniaxial Warm Compression through In-Situ Synchrotron X-ray Diffraction" Metals 11, no. 3: 467. https://doi.org/10.3390/met11030467
APA StyleBevilaqua, W. L., Epp, J., Meyer, H., Dong, J., Roelofs, H., da Silva Rocha, A., & Reguly, A. (2021). Revealing the Dynamic Transformation of Austenite to Bainite during Uniaxial Warm Compression through In-Situ Synchrotron X-ray Diffraction. Metals, 11(3), 467. https://doi.org/10.3390/met11030467