CFD–DPM Simulation Study of the Effect of Powder Layer Thickness on the SLM Spatter Behavior

Abstract

Selective Laser Melting (SLM) has significant advantages in manufacturing complex structural components and refining the alloy microstructure; however, spatter, as a phenomenon that accompanies the entire SLM forming process, is prone to problems such as inclusions, porosity, and low powder recovery quality. In this paper, a Computational Fluid Dynamics–Discrete Particle Method (CFD–DPM) simulation flow for predicting the SLM spatter behavior is established based on the open-source code OpenFOAM. Among them, the single-phase flow Navier–Stokes equation is used in the Eulerian framework to equivalently describe the effect of metal vapor and protective gas on the flow field of the forming cavity, and the DPM method is used in the Lagrangian framework to describe the metal particle motion, and the factors affecting the particle motion include particle–particle collision, particle–wall collision, fluid drag force, gravity, buoyancy force, and additional mass force. In addition, the equivalent volume force and fluid drag force are used to characterize the fluid–particle coupling interaction. For the spatter behavior and powder bed denudation phenomenon, the calculation results show that the spatter height and the drop location show a clear correlation, and the powder bed denudation phenomenon is caused by the high-speed gas flow, causing the surrounding gas to gather in the forming area, which in turn drives the motion of the powder bed particles. For the effect of powder layer thickness on spatter and powder bed denudation, the calculation results show that the effect of powder layer thickness on the number of spatters is large (when the thickness was increased from 50 μm to 100 μm, the number of spatters increased by 157%), but the effect on spatter height and drop location distribution is small. When the powder layer thickness is small, the width of the denudation zone is significantly larger, but when the powder layer reaches a certain thickness, the width of the denudation zone does not show significant changes. It should be noted that the presented model has not been directly validated by experiments so far due to the difficulty of tracking the large-scale motion of SLM spatter in real time by current experimental means.

1. Introduction

Selective Laser Melting (SLM) is a metal additive manufacturing technology that selectively melts and builds up powder layer by layer with high energy laser, and it has significant advantages in manufacturing complex structural components and refining the alloy microstructure [1]. However, the metal particles melt rapidly under the action of the high-energy beam laser to form a mesoscopic molten pool, and even some of the metal liquid vaporizes to form a metal vapor. The high-velocity metal vapor injection makes the low-pressure area above the molten pool, which causes the surrounding metal particles to tend to move toward the molten pool due to the Bernoulli effect. The agglomerated metal particles are then ejected by the metal vapor, forming the so-called spatter [2,3]. The appearance of the SLM spatter, on the one hand, tends to cause inclusions and porosity defects inside the component [4,5] and, on the other hand, reduces the powder recovery quality [6].

Spatter is a phenomenon that accompanies the entire SLM forming process. Although it is not possible to completely eliminate spatter, it is necessary to regulate the behavior of spatter. Currently, researchers have conducted some experimental studies on SLM spatter, and the main idea is to record the generation and motion of spatter with the help of real-time monitoring means such as high-speed cameras [7,8,9,10], X-ray imaging [11], and acoustic signal acquisition [12] and to study the effects of process parameters such as scanning speed [13], laser power [13], laser beam number [14], and the protective gas type and flow rate [15,16] on spatter behavior, and then to propose SLM spatter regulation strategies such as adjusting the forming cavity flow field [17] and adding nanoparticles [18]. Experimental studies play an important role in the in-depth understanding of SLM spatter, but because SLM spatter is in a dramatically changing high-temperature and high-speed environment, the cost of experimental studies is high, and it is difficult to achieve quantitative analysis, so numerical simulation becomes a necessary aid to research. At present, the numerical simulation of SLM spatter is mainly carried out from the following two aspects: on the one hand, the high-speed inlet boundary is set instead of metal vapor, and then the coupling effect between metal particles and gas phase is described by Eulerian–Lagrangian method, which is mainly concerned with the influence of metal vapor on the formation of SLM spatter [19,20]; on the other hand, the flow field of forming cavity is calculated first by Eulerian method, and then the motion of particles with a given initial velocity under the action of forming cavity flow field is calculated by Lagrangian method, which is mainly concerned with the influence of protective gas flow on the motion of SLM spatter [21,22,23,24].

In order to describe the SLM spatter behavior more completely, this paper predicts both the generation of spatter under the action of metal vapor and the motion of spatter under the action of protective gas flow with the help of the Eulerian–Lagrangian method and focuses on the effect of the powder layer thickness on the SLM spatter behavior. The Eulerian–Lagrangian simulation method used, as well as the simulation results and analysis for different powder layer thickness scenarios, are presented in the next sections.

2. CFD–DPM Simulation Method

In this paper, a study of SLM spatter behavior prediction was conducted based on the denseParticleFoam solver in the computational fluid dynamics open-source code OpenFOAM-v9 [25]. Due to the difficulty of simulating the multiphase coupling of “metal particles-mesoscopic molten pool-metal vapor-protective gas”, the mesoscopic molten pool and metal vapor were not directly predicted here, and the metal vapor was replaced by imposing a high-speed inlet boundary condition. The above simplification is based on Ly’s experimental observation [26] that 85% of the spatter is unmelted metal particles, i.e., the majority of the spatter is the so-called powder spatter. Figure 1 shows the simulation flow of the Eulerian–Lagrangian method used in this paper, in which the flow field motion in the Eulerian framework was described by the Navier–Stokes equations for single-phase flow in Computational Fluid Dynamics (CFD). The effects of metal vapor and protective gas were realized by imposing high-velocity inlet and protective gas inlet/outlet boundary conditions, and the effects of metal particles on the gas-phase flow were characterized with the help of equivalent volume force. The motion of the metal particles in the Lagrangian frame was described by the Discrete Particle Method (DPM). The particle’s motion follows Newton’s second law, and the influencing factors include particle–particle collisions, particle–wall collisions, fluid drag force, gravity, buoyancy, and additional mass force, etc. The major difference between DPM and the common Discrete Element Method [27] (DEM) is that to improve the computational efficiency, DPM takes particle packages as the object of study, and each particle package contains several particles, which have the same size, velocity, and other properties. Since the underlying code of the denseParticleFoam solver has not been changed here, the specific CFD–DPM theoretical model can be found in the official documentation of OpenFOAM-v9 [25].

3. Results and Discussion

The metal particle material used herein is 316 L stainless steel with a density of 7800 kg/m³, Young’s modulus of 2.2 GPa, and Poisson’s ratio of 0.3. Other particle properties include that the particle type is collidingCloud, the number of particles inside the particle parcel is 1, the particles’ diameter satisfies a normal distribution (center value of 40 μm, variance of 5 μm, maximum value of 55 μm, and minimum value of 25 μm), the particle–particle collision model has a restitution coefficient of 0.9, a spring index of 1.5, and a friction coefficient of 0.62, and the particles’ initial positions are obtained by the calculation of the open-source DEM code Yade [28]. The protective gas used is nitrogen, with a density of 1.17 kg/m³ and a kinetic viscosity of 1.18 × 10⁻⁵ Pa·s. The protective gas is considered an incompressible Newtonian fluid, and the LES turbulence model is introduced in the flow field calculation.

Figure 2 shows the geometry and mesh model used. The geometry of the forming chamber is 100 × 5 × 50 mm, and the height of the protective gas inlet/outlet is 15 mm and 10 mm from the bottom surface of the forming cavity. The lower bottom surface has a projection for powder storage with a geometry of 10 × 5 × 0.3 mm, and the projection is 10 mm from the right side wall. The mesh size has a large impact on the accuracy of Eulerian–Lagrangian coupling calculations, and Ref. [29] suggests that for non-resolved Eulerian–Lagrangian coupling calculations, the mesh size should be taken as 2–4 times the average particle size. In order to control the number of computational cells as much as possible on the basis of the fine enough mesh in the powder layer area, this paper adopts the blockMesh function that comes with OpenFOAM for non-uniform meshing, in which the mesh size is 0.1 mm in both X- and Y-direction, and the mesh size in Z-direction transitions from 0.1 mm to 0.3125 mm according to certain rules. The total number of nodes of the mesh is 13,084,509, and the total number of cells is 12,765,000. The inlet flow rate of the protective gas is 1 m/s, the size of the high-speed inlet of the equivalent metal vapor is 100 × 100 μm, and the flow rate of the high-speed inlet is 30 m/s in the Z-direction, which moves along the midline of the bottom surface of the powder bed with a speed of 0.2 m/s (Figure 2c), and this moving boundary is realized with the help of the codedFixedValue boundary type. Considering the real situation where the spatter may collide with the side walls, fall into the powder bed or escape through the protective gas outlet, the interaction type between the protective gas outlet and the particle is set to escape, the interaction type between the bottom surface of the forming cavity and the particle is set to stick, and the interaction type between the other boundaries and the particle is set to rebound (the restitution coefficient is 0.9, and the friction coefficient is 0.62). The adopted conservation equations, boundary conditions, and initial conditions are given in

Table 1. Adopted conservation equations, boundary conditions, and initial conditions.

CFD model for fluid phase	$\frac{\partial {\rho }_f{\stackrel{\rightharpoonup }{u}}_f}{\partial t}+\nabla \cdot \left({\rho }_f{\stackrel{\rightharpoonup }{u}}_f\otimes {\stackrel{\rightharpoonup }{u}}_f\right)=-\nabla p_f+{\mu }_f\left(\nabla \stackrel{\rightharpoonup }{u}+\nabla {\stackrel{\rightharpoonup }{u}}^T\right)+\nabla \cdot {\overline{\overline{\tau }}}_{sgs}+{\rho }_f\stackrel{\rightharpoonup }{g}+{\stackrel{\rightharpoonup }{f}}_{p-f}$ $\nabla \cdot {\stackrel{\rightharpoonup }{u}}_f=0$
DPM model for particle phase	$m_p\frac{d{\stackrel{\rightharpoonup }{u}}_p}{dt}={\stackrel{\rightharpoonup }{F}}_{f-p}+{\stackrel{\rightharpoonup }{F}}_g+{\stackrel{\rightharpoonup }{F}}_p+{\stackrel{\rightharpoonup }{F}}_a+{\displaystyle \sum \left({\stackrel{\rightharpoonup }{F}}_n+{\stackrel{\rightharpoonup }{F}}_t\right)}$ $I_p\frac{{d\stackrel{\rightharpoonup }{\mathsf{\omega }}}_p}{\mathrm{dt}}={\displaystyle \sum \stackrel{\rightharpoonup }{R}\times {\stackrel{\rightharpoonup }{F}}_t}$
CFD–DPM coupling strategy	${\stackrel{\rightharpoonup }{F}}_{f-p}=\frac{{\mathsf{\pi }\mathsf{\rho }}_f{C}_d{D}_p^2}{8}\left({\stackrel{\rightharpoonup }{u}}_f-{\stackrel{\rightharpoonup }{u}}_p\right)\left|{\stackrel{\rightharpoonup }{u}}_f-{\stackrel{\rightharpoonup }{u}}_p\right|$ ${\stackrel{\rightharpoonup }{f}}_{p-f}=-\frac{{\displaystyle \sum {\stackrel{\rightharpoonup }{F}}_{f-p}}}{V_{\mathrm{cell}}}$
Boundary conditions	The inlet flow rate of the protective gas is 1 m/s, and the flow rate of the high-speed inlet of the equivalent metal vapor is 30 m/s in the Z direction. The interaction type between the protective gas outlet and the particle is escape, the interaction type between the bottom surface of the forming cavity and the particle is stick, and the interaction type between the other boundaries and the particle is rebound.
Initial conditions	The initial velocity of the forming cavity flow field is zero. The initial velocity of the particles is zero.

.

In Table 1, ${\rho }_f$ is the fluid-phase density; ${\stackrel{\rightharpoonup }{u}}_f$ is the fluid-phase velocity; $t$ is time; $p_f$ is the fluid-phase pressure; ${\mu }_f$ is the fluid-phase dynamic viscosity; ${\overline{\overline{\tau }}}_{sgs}$ is the sub-grid stress tensor obtained by introducing the LES turbulence model; $\stackrel{\rightharpoonup }{g}$ is the gravitational acceleration; ${\stackrel{\rightharpoonup }{f}}_{p-f}$ is the force of the particle phase on the fluid phase; $m_p$ is the particle mass; ${\stackrel{\rightharpoonup }{u}}_p$ is the particle velocity; ${\stackrel{\rightharpoonup }{F}}_{f-p}$ is the drag force of the fluid phase on the particle phase; ${\stackrel{\rightharpoonup }{F}}_g$ is the sum of gravitational and buoyant forces on the particle phase; ${\stackrel{\rightharpoonup }{F}}_p$ characterizes the effect of non-uniform pressure distribution on the particle motion; ${\stackrel{\rightharpoonup }{F}}_a$ is the additional mass force; ${\stackrel{\rightharpoonup }{F}}_n$ and ${\stackrel{\rightharpoonup }{F}}_t$ are the normal and tangential forces generated by the particle collision, respectively; $I_p$ is the rotational inertia of the particle; ${\stackrel{\rightharpoonup }{\omega }}_p$ is the angular velocity of rotation of the particle; $\stackrel{\rightharpoonup }{R}$ is the rotation force arm; ${\rho }_p$ is the particle-phase density; $D_p$ is the particle diameter; $C_d$ is the drag force coefficient; $V_{\mathrm{cell}}$ is the volume of a single mesh cell.

In order to obtain the stable forming cavity flow field first, the high-speed inlet boundary condition takes effect at 0.2 s, and the total physical simulation time is 0.45 s. Considering that the number of particles in a single core during the denseParticleFoam solver calculation has a large impact on the computational efficiency, a manual mesh partitioning scheme is used here to realize more cores to participate in the particle motion calculation.

Table 2. Simulation schemes to study the effect of powder layer thickness on the SLM spatter behavior.

Simulation Scheme	Powder Layer Thickness (μm)	Number of Particles
Scheme A	50	26,598
Scheme B	70	39,839
Scheme C	90	52,913
Scheme D	100	61,441

lists the simulation schemes designed to investigate the effect of powder layer thickness on the SLM spatter behavior, and

Table 3. Calculation information for different simulation schemes.

Simulation Scheme	Computational Configuration	Number of Cores Used for Calculation	Physical Time Period (s)	Time Step (μs)	Time Consumption (h)
Scheme A	Intel Xeon Gold 6240 CPU (dual CPU, 72 threads, 128 GB RAM)	68	0–0.2	50	120.3
			0.2–0.24	5	192.0
			0.24–0.45	50	234.4
Scheme B	Intel Xeon Gold 6240 CPU (dual CPU, 72 threads, 128 GB RAM)	68	0–0.2	50	122.4
			0.2–0.24	5	182.0
			0.24–0.45	50	271.7
Scheme C	Intel Xeon Gold 5120 CPU (dual CPU, 56 threads, 96 GB RAM)	52	0–0.2	50	106.7
			0.2–0.24	5	139.4
			0.24–0.45	50	242.5
Scheme D	Intel Xeon Gold 5120 CPU (dual CPU, 56 threads, 96 GB RAM)	52	0–0.2	50	107.3
			0.2–0.24	5	141.2
			0.24–0.45	50	255.4

gives the computational information for the different simulation schemes. From the computational information, it is clear that the CFD–DPM simulation is significantly more time-consuming than the usual pure flow field motion calculation because it involves the coupled solution of flow field motion and particle motion.

The gas-phase flow speed, isospeed line, and particle distributions at different moments for Scheme B are given in Figure 3. From the calculation results, it can be seen that the protective gas flows into the forming cavity at a certain flow rate, and the flow field in the forming cavity basically reaches stability at t = 0.2 s (Figure 3(a2,b2)). When the boundary condition of the high-speed inlet, which characterizes the influence of metal vapor, starts to take effect, the powder bed particles are ejected under the drag effect of the high-speed gas flow, forming spatters (Figure 3(c1,c2)), and at the same time, the high-speed gas flow and spatters have obvious influence on the local flow field in the forming cavity (Figure 3(a3,b3)); when the high-speed gas flow stops acting, the formed spatters move to the side of the protective gas outlet under the joint action of the protective gas flow and gravity (Figure 3(c3–c5)), and the flow field in the forming cavity gradually returns to stability (Figure 3(a5,b5)).

To visualize the spatter behavior and powder bed denudation phenomenon, the particle motion and gas-phase flow at different moments in Scheme B are given in Figure 4. From the calculation results, it can be seen that the powder bed particles form spatters under the action of high-speed gas flow and cause a blank area above the high-speed gas flow action zone (Figure 4(a1)), but as the high-speed gas flow action zone keeps moving, the original blank area is gradually refilled by the surrounding metal particles, which is the so-called powder bed denudation phenomenon (Figure 4(a3)). Figure 4(b2) gives the velocity distribution of particles near the action zone of high-speed gas flow at t = 0.22 s. It is evident that the particles near the action zone have a tendency to gather towards the action zone, which is caused by the Bernoulli effect, i.e., the high-speed gas flow zone is a low-pressure zone, which in turn triggers the surrounding gas to gather towards the high-speed gas flow zone, thus driving the metal particles to gather towards the action zone (Figure 4c). In order to analyze the influence range of powder bed denudation, the powder bed denudation zone at different moments is given in Figure 5. The criterion for judging the powder bed denudation zone here is that if the movement speed of metal particles (excluding spatters) exceeds 0.001 m/s, it is considered to be affected by powder bed denudation. From the comparison results, it can be seen that the width of the powder bed denudation zone is basically the same at different moments. Figure 6 gives the spatter trajectory at different moments under Scheme B. From the calculation results, it can be seen that the spatters as a whole show the movement law of rising under the action of high-speed gas flow and then falling under the action of protective gas flow and gravity, while the spatter height and drop location show an obvious correlation and a wide range of distribution.

The particle distributions under different simulation schemes are given in Figure 7 and Figure 8. From the comparison results, it can be seen that the overall motion pattern of the spatters under different powder layer thicknesses is basically the same. In addition, from the spatter distribution in the main view and the side view, it is found that the larger the powder layer thickness is, the larger the number of spatters is. Figure 9a gives the variation curves of the number of spatters at different moments under different powder layer thicknesses. From the comparison results, it can be seen that when the powder layer thickness is certain, the number of spatters gradually increases as the action time of the high-speed gas flow increases. The reason is that the action time of the high-speed gas flow and the length of the powder bed set herein are limited, and most of the spatters have not yet fallen into the substrate or the powder bed. If the action time of the high-speed gas flow and the length of the powder bed are sufficient, it can be expected that the number of spatters will reach a stable value. As the powder layer thickness increases, the number of spatters increases significantly. The reason is that the larger the powder layer thickness, the more metal particles are affected by the high-speed gas flow. Figure 9b gives the experimentally measured spatter numbers for different powder layer thicknesses in Ref. [30], and in terms of the distribution trend, the spatter numbers increase gradually as the powder layer thickness increases, which is consistent with the simulation results here. It should be noted that the experimental result in Figure 9b serves mainly as a qualitative comparison; in fact, the current experimental means are extremely difficult to capture spatters running at high speeds on a large scale. The reason for the large difference between the spatter number in Figure 9b and that in Figure 9a is that a light-sensitive camera was used in Ref. [30] to photograph the SLM forming process to determine the spatter number, and the light-sensitive camera can only distinguish the spatters with higher temperature, which is called hot spatter.

To analyze the effect of powder layer thickness on powder bed denudation, the denudation zone widths at different powder layer thicknesses are given in Figure 9c. From the comparison results, it can be seen that when the powder layer thickness is small, the denudation zone width is significantly larger. The reason for this phenomenon is that the gas-phase flow triggered by the Bernoulli effect only forms a drag effect on the metal particles on the surface of the powder layer, and when the powder layer thickness is small, the particles below the powder layer have limited ability to hinder the particles’ movement on the surface of the powder layer, which in turn causes a larger denudation zone width. With the gradual increase in the powder bed thickness, the denudation zone width decreases significantly and reaches stability. The reason for this is that when the powder layer thickness is large, the obstruction ability of the particles below the powder layer to the particles’ movement on the surface of the powder layer increases significantly, which makes the denudation zone width decrease significantly, but when the powder layer thickness is too large, the obstruction ability of the particles below the powder layer to the particles movement on the surface of the powder layer does not improve significantly, which makes the denudation zone width remain stable. In order to analyze the effect of powder layer thickness on the spatter height, the maximum height of spatters at different powder layer thicknesses is given in Figure 9d. From the comparison results, it can be seen that there is not much difference in the maximum height of spatters under different powder layer thicknesses. It can be seen that the influence of the powder layer thickness on the spatter height is small.

In order to analyze the influence of the powder layer thickness on the final drop locations of the spatters, the final trajectory of the spatters under different simulation schemes is given in Figure 10. From the calculation results, it can be seen that the spatter movement can be divided into four categories: the first is to fall directly into the substrate on the left side of the powder bed under the combined effect of protective gas drag and gravity, the second is to escape from the forming cavity through the protective gas outlet, the third is to fall into the substrate on the left side of the powder bed after hitting the wall of the forming cavity, and the fourth is to fall back into the powder bed or the substrate area adjacent to the powder bed, among which the number of spatters in the first category is the largest. In order to quantify the distribution of the final drop locations of the spatters on the substrate on the left side of the powder bed under different layer thicknesses, the distribution of the number of spatters in the interval width of 4 mm for different simulation schemes is given in Figure 11. From the comparison results, it can be seen that, on the one hand, the number of spatters in the same X-directional interval gradually increases with the increase in powder layer thickness for different simulation schemes; on the other hand, the number of spatters in different X-directional intervals for a single simulation scheme is basically the same. It can be seen that the powder layer thickness mainly affects the number of spatters, and its influence on the distribution of spatters’ drop locations is relatively small. It should be noted that the reason for the high number of spatters in the 0–4 mm range in Figure 11 is that most of the spatters that hit the wall and then fall into the substrate are in this range.

4. Conclusions

(1)

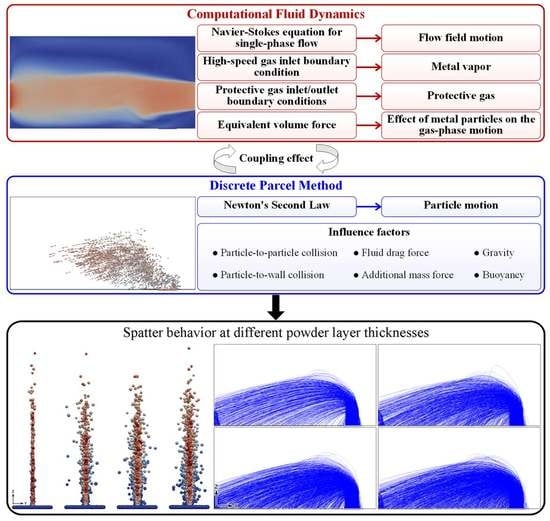
In this paper, a study on the prediction of SLM spatter behavior is carried out based on the denseParticleFoam solver in the CFD open-source code OpenFOAM-v9, in which the single-phase flow N-S equation is used to equivalently describe the effect of metal vapor and protective gas on the flow field of the forming cavity in the Eulerian framework, and the DPM method is used to describe the metal particle motion in the Lagrangian framework. In addition, the equivalent volume force and the fluid drag force are used to characterize the interaction forces between the fluid and the particles, respectively.

(2)

For the spatter behavior and powder bed denudation phenomenon, the calculation results show that the spatter height and drop location show a clear correlation, and the powder bed denudation phenomenon is caused by the Bernoulli effect triggered by the high-speed gas flow, which causes the surrounding gas to gather in the high-speed gas flow area, thus driving the powder bed particles to gather in the forming zone.

(3)

For the effect of powder layer thickness on spatter and powder bed denudation, the calculation results show that the number of spatters increases significantly with the increase in powder layer thickness; meanwhile, the effect of powder layer thickness on spatter height and drop location distribution is small. When the powder layer thickness is small, the denudation zone width is obviously larger, but when the powder layer reaches a certain thickness, the denudation zone width does not show significant changes.

(4)

Since the main objective of this paper is to establish a simulation flow to describe the SLM spatter behavior, the subsequent research will focus on setting the computational parameters more rationally to achieve quantitative prediction of the SLM spatter.